數(shù)制也稱計數(shù)制,是用一組固定的符號和統(tǒng)一的規(guī)則來表示數(shù)值的方法。
任何一個數(shù)制都包含兩個基本要素:基數(shù)和位權(quán)。
基數(shù):數(shù)制所使用數(shù)碼的個數(shù)。
例如,二進(jìn)制的基數(shù)為2;十進(jìn)制的基數(shù)為10。
位權(quán):?數(shù)制中某一位上的1所表示數(shù)值的大小(所處位置的價值)。
例如,十進(jìn)制的123,1的位權(quán)是100,2的位權(quán)是10,3的位權(quán)是1。
二進(jìn)制中的 1011 ,左起第一個1的位權(quán)是8,0的位權(quán)是4,第二個1的位權(quán)是2,第三個1的位權(quán)是1。
PLC中常用的數(shù)制有:十進(jìn)制、二進(jìn)制、十六進(jìn)制、八進(jìn)制等。
此外還有BCD碼和ASCII碼也偶爾會使用。
十進(jìn)制(Decimal?notation):
如1234=1*103+2*102+3*101+4*100,逢十進(jìn)一,基數(shù)為10,單個數(shù)是0-9,每位的系數(shù)乘于基數(shù)(10)的N次方,N為其所處的位數(shù)。?
二進(jìn)制(Binary?notation):
如1101=1*23+1*22+0*21+1*20=13,逢二進(jìn)一,基數(shù)為2,單個數(shù)只有0和1, 每位的系數(shù)乘于基數(shù)(10)的N次方,N為其所處的位數(shù)。從第3位至0分別為8,4,2,1,所以二進(jìn)制也成8421碼。如果表示有符號數(shù),則用最高位表示符號,0為正數(shù)1為負(fù)數(shù)。正數(shù)以二進(jìn)制原碼表示;負(fù)數(shù)則以補(bǔ)碼存儲,即將原碼逐位取反再加1。
十六進(jìn)制(Hexdecimal?notation):
逢16進(jìn)1的進(jìn)位制。一般用數(shù)字0到9和字母A到F(或a~f)表示,其中:A~F表示10~15,這些稱作十六進(jìn)制數(shù)字。
八進(jìn)制(Octal?notation):
逢八進(jìn)一,單個數(shù)有0-7,在PLC中常用于編址,數(shù)據(jù)運算應(yīng)用較少。BCD碼(Binary-Coded Decimal?):亦稱二進(jìn)碼十進(jìn)數(shù)或二十進(jìn)制代碼。用4位二進(jìn)制數(shù)來表示1位十進(jìn)制數(shù)中的0~9這10個數(shù)碼。通常時鐘采用BCD碼存儲。
ASCII(American Standard Code for Information Interchange:美國信息交換標(biāo)準(zhǔn)代碼):
是基于拉丁字母的一套電腦編碼系統(tǒng),主要用于顯示現(xiàn)代英語和其他西歐語言。它是現(xiàn)今最通用的系統(tǒng),并等同于國際標(biāo)準(zhǔn)ISO/IEC 646。PLC中數(shù)據(jù)存儲只能以0和1形式,其它數(shù)據(jù)可通過進(jìn)制轉(zhuǎn)換成二進(jìn)制,但是字母和一些特殊符號用什么表示則需要約定一套轉(zhuǎn)換規(guī)則,于是美國有關(guān)的標(biāo)準(zhǔn)化組織就出臺了ASCII編碼。
浮點數(shù)(float):
又稱實數(shù)(REAL),浮點數(shù)是屬于有理數(shù)中某特定子集的數(shù)的數(shù)字表示,在計算機(jī)中用于近似表示任意某個實數(shù)。具體來說,這個實數(shù)由一個整數(shù)或定點數(shù)(即尾數(shù))乘以某個基數(shù)(計算機(jī)中通常是2)的整數(shù)次冪得到,這種表示方法類似于基數(shù)為10的科學(xué)計數(shù)法。
在二進(jìn)制科學(xué)表示法中:S=M×2^N
主要由三部分構(gòu)成:符號位+階碼(N)+尾數(shù)(M)。對于float型數(shù)據(jù),其二進(jìn)制有32位,其中符號位1位,階碼8位,尾數(shù)23位。
符號位:0表示正,1表示負(fù)。
階碼:這里階碼采用移碼表示,對于float型數(shù)據(jù)其規(guī)定的偏置量為127,階碼有正有負(fù),對于8位二進(jìn)制,則其表示范圍為?128~127。比如,對于float型數(shù)據(jù),若階碼的真實值為2,則加上127后為129,其階碼表示形式為10000010。
尾數(shù):有效數(shù)字位,即部分二進(jìn)制位(小數(shù)點后面的二進(jìn)制位),因為規(guī)定M的整數(shù)部分恒為1,所以這個1就不進(jìn)行存儲了。
舉例說明 ? ?
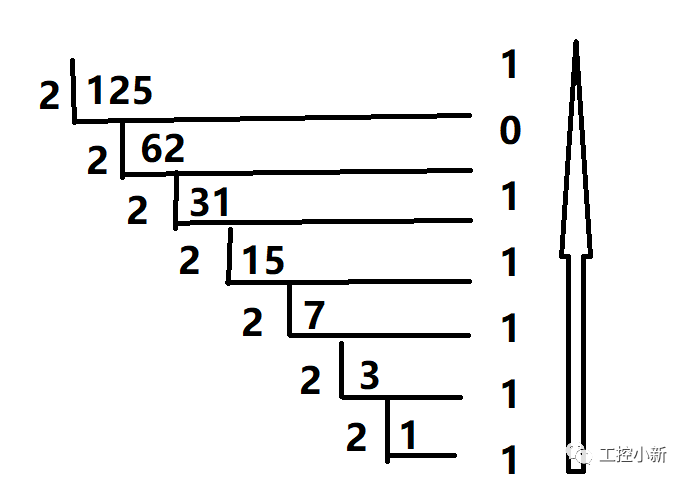
float型數(shù)據(jù)125.5轉(zhuǎn)換為標(biāo)準(zhǔn)浮點格式,125的二進(jìn)制表示形式為1111101,小數(shù)部分表示為二進(jìn)制為 1(小數(shù)部分乘以2,小于1則為0,大于1則為1,小數(shù)繼續(xù)乘以2,直到小數(shù)部分為0為止),則125.5二進(jìn)制表示為1111101.1,由于規(guī)定尾數(shù)的整數(shù)部分恒為1,則表示為1.1111011*2^6,階碼為6,加上127為133,則表示為10000101,而對于尾數(shù)將整數(shù)部分1去掉,為1111011,在其后面補(bǔ)0使其位數(shù)達(dá)到23位,則為11110110000000000000000。則其二進(jìn)制表示形式為:0 10000101 11110110000000000000000
那么這些進(jìn)制之間是如何轉(zhuǎn)換呢? ? ?
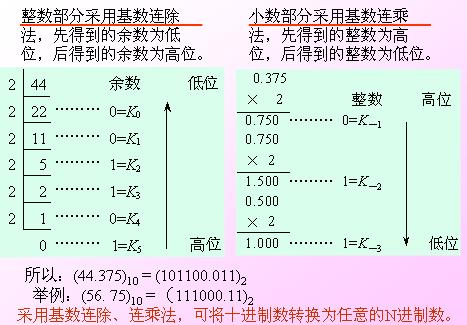
1.十進(jìn)制轉(zhuǎn)二進(jìn)制方法為:
十進(jìn)制數(shù)除2取余法,即十進(jìn)制數(shù)除2,余數(shù)為權(quán)位上的數(shù),得到的商值繼續(xù)除2,依此步驟繼續(xù)向下運算直到商為0為止。(具體用法如下圖)
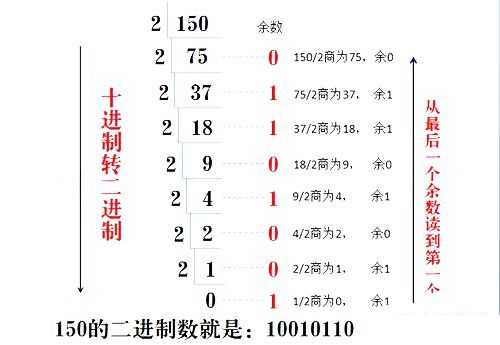
2.二進(jìn)制轉(zhuǎn)十進(jìn)制方法為:
把二進(jìn)制數(shù)按權(quán)展開、相加即得十進(jìn)制數(shù)。(具體用法如下圖)
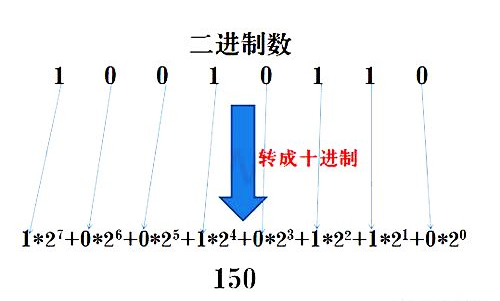
3.二進(jìn)制轉(zhuǎn)八進(jìn)制方法為:
3位二進(jìn)制數(shù)按權(quán)展開相加得到1位八進(jìn)制數(shù)。(注意事項,3位二進(jìn)制轉(zhuǎn)成八進(jìn)制是從右到左開始轉(zhuǎn)換,不足時補(bǔ)0)。(具體用法如下圖)
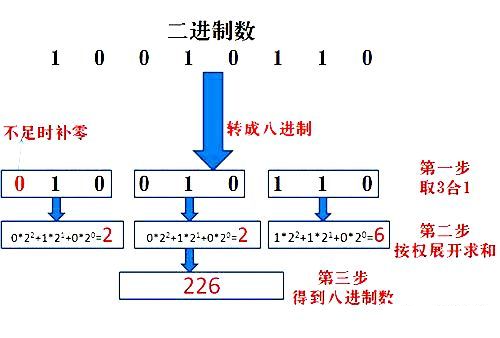
4.八進(jìn)制轉(zhuǎn)成二進(jìn)制方法為:
八進(jìn)制數(shù)通過除2取余法,得到二進(jìn)制數(shù),對每個八進(jìn)制為3個二進(jìn)制,不足時在最左邊補(bǔ)零。(具體用法如下圖)
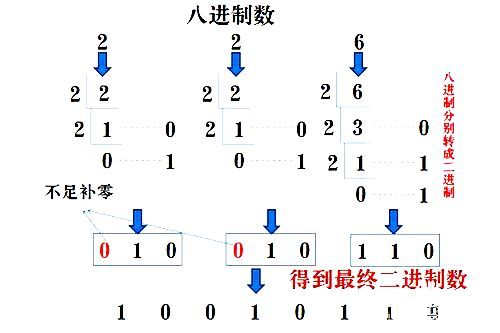
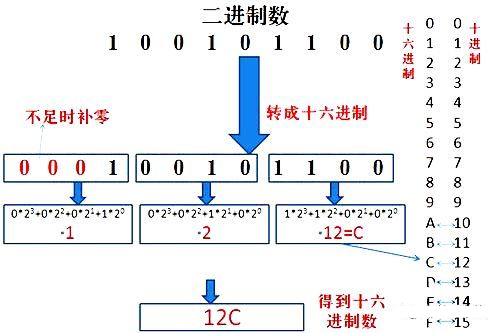
5.二進(jìn)制轉(zhuǎn)十六進(jìn)制方法為:
與二進(jìn)制轉(zhuǎn)八進(jìn)制方法近似,八進(jìn)制是取三合一,十六進(jìn)制是取四合一。(注意事項,4位二進(jìn)制轉(zhuǎn)成十六進(jìn)制是從右到左開始轉(zhuǎn)換,不足時補(bǔ)0)。(具體用法如下圖)
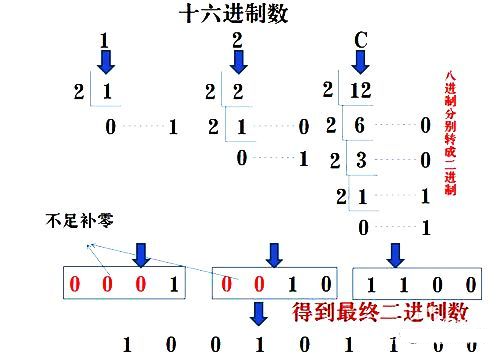
6.十六進(jìn)制轉(zhuǎn)二進(jìn)制方法為:
十六進(jìn)制數(shù)通過除2取余法,得到二進(jìn)制數(shù),對每個十六進(jìn)制為4個二進(jìn)制,不足時在最左邊補(bǔ)零。(具體用法如下圖)
?
7.十進(jìn)制轉(zhuǎn)八進(jìn)制或者十六進(jìn)制有兩種方法:
第一:間接法—把十進(jìn)制轉(zhuǎn)成二進(jìn)制,然后再由二進(jìn)制轉(zhuǎn)成八進(jìn)制或者十六進(jìn)制。這里不再做圖片用法解釋。
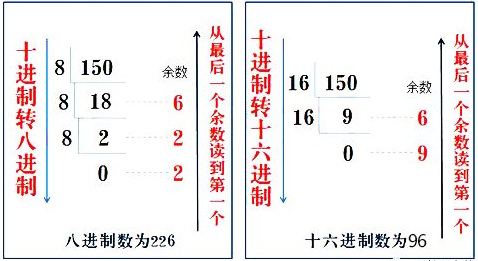
第二:直接法—把十進(jìn)制轉(zhuǎn)八進(jìn)制或者十六進(jìn)制按照除8或者16取余,直到商為0為止。(具體用法如下圖)
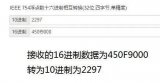
8.八進(jìn)制或者十六進(jìn)制轉(zhuǎn)成十進(jìn)制方法為:
把八進(jìn)制、十六進(jìn)制數(shù)按權(quán)展開、相加即得十進(jìn)制數(shù)。(具體用法如下圖)

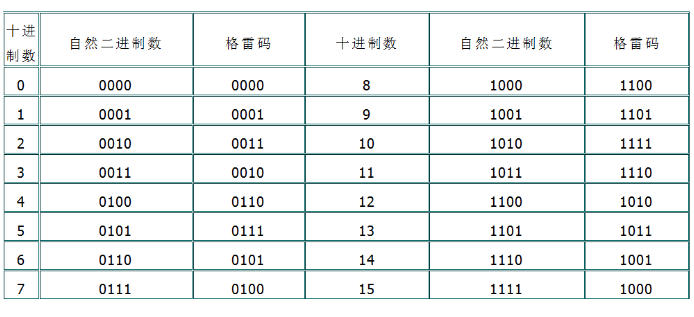
9.BCD碼轉(zhuǎn)十進(jìn)制:
因為BCD碼是用四位二進(jìn)制表示一位十進(jìn)制數(shù),所以轉(zhuǎn)換方法類似二進(jìn)制轉(zhuǎn)十六進(jìn)制“取四合一”法,四位組合后轉(zhuǎn)成十進(jìn)制得到的就是十進(jìn)制。以上介紹了PLC中常用進(jìn)制及相互轉(zhuǎn)換方法,意在讓初學(xué)者理解進(jìn)制含義及轉(zhuǎn)換規(guī)律。真正使用時可利用計算機(jī)提供的程序員型計算器輕松運算出來。
審核編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App









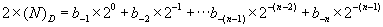
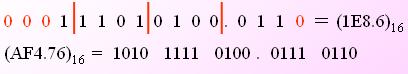

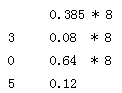
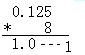
















評論