信號頻譜分析和測試
1.了解周期函數的傅立葉變換理論及虛擬頻譜分析儀的工作原理;
2.熟悉典型信號的波形和頻譜特征,并能夠從信號頻譜中讀取所需的信息。
二、實驗要求
1.測量典型信號(正弦波、三角波、方波)的頻譜并記錄;
2、測量由基波、二次諧波、三次諧波的組合波形的頻譜并計錄。
三、實驗器材
1.SJ-8002B電子測量實驗箱 ???????????????????????????? 1臺
2.雙蹤示波器(20MHz模擬或數字示波器)???????????????? 1臺
3.函數信號發生器或數字存儲示波器(1Hz~1MHz)???????? 1臺
4.計算機(具有運行windows2000和圖形化控件的能力)?????? 1臺
四、實驗原理
??? 1.非正弦周期函數的傅立葉分解
?? (1).定義
??? 如果給定的周期函數滿足狄里赫利條件(函數在任意有限區間內,具有有限個極值點與不連續點),則該周期函數定可展開為一個收斂的正弦函數級數。而在電工技術中,我們所遇到的周期函數通常均滿足該條件。這樣
其中,兩式中的各個系數的計算公式及對應的系數的關系
在該展開式中,稱為周期函數的恒定分量,也稱為直流分量;與原周期函數的周期相同的正弦分量稱為一次諧波,也稱為基波分量。其他各項稱為高次諧波(如2次諧波、3次諧波等等)
?? (2).各種常用周期信號的傅立葉展開
?????? 方波
,其中的
?????? 三角波
,其中的
?????? 鋸齒波
,其中
?? 2.非正弦周期函數的有效值
?? 以電流為例,周期電壓、電流的有效值的定義為:
?? 前面已經談到,任意周期函數均可展開為傅立葉級數:
?? 代入有效值的定義式:
?? 積分號內的平方式展開有以下幾種情況:
??
??
??
??
因此,的有效值為:。其中,為各個n次諧波分量的有效值。同理,任意電壓的有效值為:,其中,為各n次諧波分量的有效值。
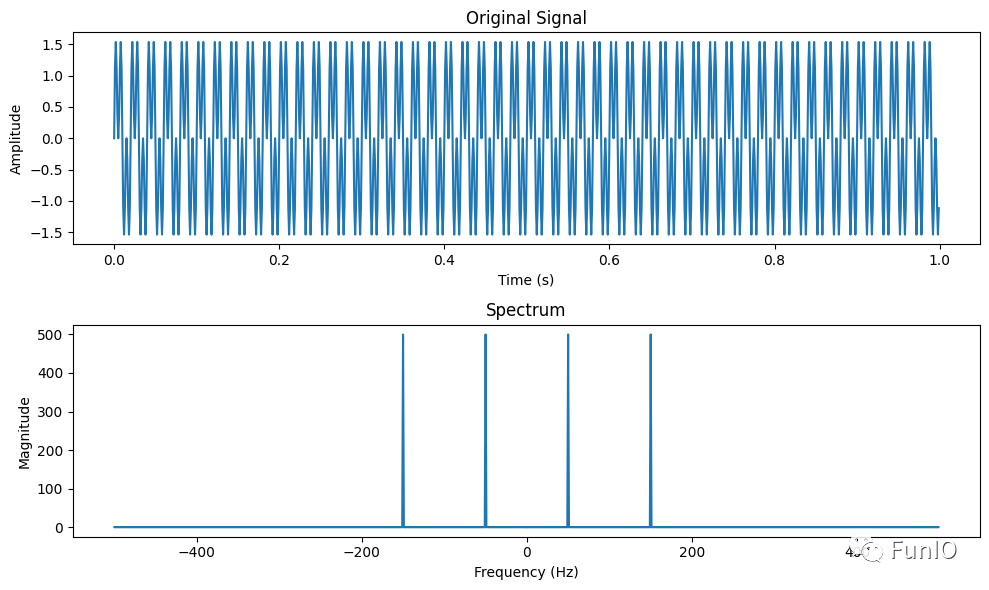
?? 3.頻譜
?? (1).非正弦周期函數的頻譜
??? 對某函數以頻率為橫軸,各個頻率對應的正弦函數的幅值為縱軸所繪出的線段系稱為該函數的頻譜。
??? 對于周期函數而言,其頻譜為一系列譜線。如
?? 方波
????????????
圖4 矩形波的傅立葉頻譜
??? 三角波
?????????
圖5 三角波的傅立葉頻譜
???? 鋸齒波
??????????
圖6 鋸齒波的傅立葉頻譜
?
?? (2). 傅立葉變換與頻譜函數
??? 1).周期函數的傅立葉級數的指數形式
? ??
?? 令,且對所有,均有,則,其中,
? 2).幅度頻譜與相位頻譜
- 體現||與頻率之間的關系的譜線,稱為幅度頻譜。
?? 由于指數級數中的k可以分別取相應的正負值,因此幅度頻譜關于Y軸對稱;而其譜線的高度僅為付氏頻譜譜線高度的一半。例如方波
??????????? ?
???? ??
??????????????????????????????? 圖7 方波及其傅立葉頻譜、幅度譜
4.信號的離散傅立葉變換(DFT)
?? x(t)經采樣后變為x(nT’),T’為采樣周期,采樣頻率fs=1/T’。離散信號x(nT’)的傅里葉變換可以表示為:
??? ,n=0,1,…N-1
??? X(k)是復數,信號的頻譜是它的模,為了方便顯示,做歸一化處理,用來表示頻譜。
?? 頻率分辨率為:
??
?? FFT是DFT的快速算法。
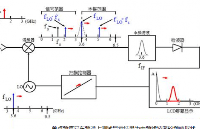
?? 5. 虛擬頻譜分析儀
?? 數字式虛擬頻譜分析儀是通過A/D采樣器件,將模擬信號轉換為數字信號,傳給微處理器系統或計算機來處理.在對交流信號的測量中,根據奈奎斯特采樣定理,采樣速率必須是信號頻率的兩倍以上,采樣頻率越高,時間軸上的信號分辨力就越高,所獲得的信號就越接近原始信號,在頻譜上展現的頻帶就越寬。
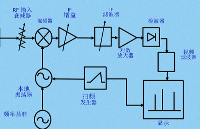
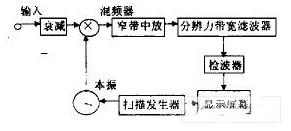
??? 本頻譜分析儀采用快速傅立葉變換的方法,分析信號中所含各個頻率份量的幅值。其構成框圖如圖8所示:
????????????????
圖8頻譜分析儀框圖
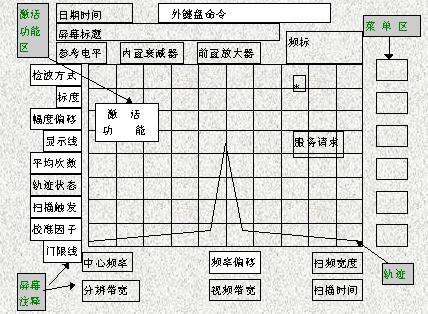
?? 頻譜儀界面如圖9所示。
?? 說明:1. 頻譜儀的縱軸為幅度(有效值)。
???????? 2.改變參數時,請先停止測量
???????? 3.改變內部信號源時,請先停止測量
???????? 4.由于本實驗平臺的A/D分辨率只有8位,決定了頻譜分析的精度不高,同學們重點掌握頻譜分析的方法。
圖9 頻譜儀界面
五、實驗步驟
?? 1.測量典型信號(正弦波、三角波、方波)的頻譜
??? 1.1? 用Q9線連接信號發生器與實驗平臺的Ain1端,并用EPP排線連接實驗平臺和計算機之間的EPP接口,最后打開電源。接線圖如圖10所示。有使用外部信號源和內部信號源兩種連線方法,S102短路塊放于左邊,可外接示波器在Ain2檢測輸入信號波形。
??? ????????????????????
? ???????????????????????????????????????? 圖10?? 接線圖
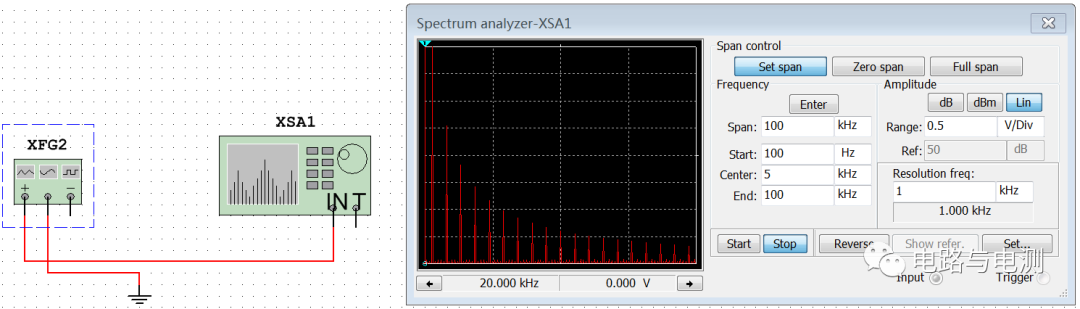
?? 信號發生器產生一個頻率為10K,峰值為3V左右的正弦波,啟動實驗平臺配套的頻譜分析軟件,其界面如下圖所示意。
????? ??????????
????????????????????????????????????????? 圖11 虛擬頻譜分析儀界面
??? 1.2? 由信號源產生一個頻率為10KHz,峰值為3V的正弦波,用數字頻譜分析儀對該信號進行頻譜測量,幅度刻度方式設為線性刻度,不加窗函數,起始頻率為0Hz,結束頻率為100KHz,Y線性參考電壓為2V,將測量結果填入表1,并計算出頻譜的理論值填入表1。
????????????????????????????????????????????? 表1
|
? |
基波 |
二次諧波 |
三次諧波 |
四次諧波 |
五次諧波 |
六次諧波 |
七次諧波 |
|
頻率(Hz) |
? |
? |
? |
? |
? |
? |
? |
|
測量幅度 |
? |
? |
? |
? |
? |
? |
? |
|
幅度理論值 |
? |
? |
? |
? |
? |
? |
? |
?? 1.3 由信號源產生一個頻率為10KHz,峰值為3V的三角波,用數字頻譜分析儀對該信號進行頻譜測量,幅度刻度方式設為線性刻度,不加窗函數,起始頻率為0Hz,結束頻率為100KHz,Y線性參考電壓為2V,將測量結果填入表2,并計算出頻譜的理論值填入表2。
?????????????????????????????????????????????????????? 表2
|
? |
基波 |
二次諧波 |
三次諧波 |
四次諧波 |
五次諧波 |
六次諧波 |
七次諧波 |
|
頻率(Hz) |
? |
? |
? |
? |
? |
? |
? |
|
測量幅度 |
? |
? |
? |
? |
? |
? |
? |
|
理論有效值(V) |
? |
? |
? |
? |
? |
? |
? |
??? 1.4 由信號源產生一個頻率為10KHz,峰值為4V的方波,用數字頻譜分析儀對該信號進行頻譜測量,幅度刻度方式設為線性刻度,不加窗函數,起始頻率為0Hz,結束頻率為100KHz,Y線性參考電壓為5V,將測量結果填入表3,并計算出頻譜的理論值填入表3。
表3
|
? |
基波 |
二次諧波 |
三次諧波 |
四次諧波 |
五次諧波 |
六次諧波 |
七次諧波 |
|
頻率(Hz) |
? |
? |
? |
? |
? |
? |
? |
|
測量幅度 |
? |
? |
? |
? |
? |
? |
? |
|
幅度理論值(V) |
? |
? |
? |
? |
? |
? |
? |
?? 2. 用實驗平臺的DDS信號源產生一個由基波、二次諧波、三次諧波的組合波形,觀察其頻譜
?? (1)連接實驗箱的Aout1到Ain1,進入DDS信號源程序界面,選擇“任意波形”,彈出窗口如圖12所示。
?? (2)在組合波形界面的左下方輸入基波、二次諧波、三次諧波的系數,相位延遲角度取0,點擊“繪圖”,右上方的顯示窗顯示生成的組合波形,點擊“數據寫入Aout1”,選擇組合波形的幅度(峰峰值),頻率(基波頻率),最后點擊“啟動”,則從Aout1輸出要求的信號,可外接示波器觀察。
?? (3)回到頻譜分析界面,測量組合波形頻譜,注意選擇的結束頻率比3次諧波稍大即可。
?? (4)觀察各次諧波的頻率和幅度,它們的比值關系滿足設定的系數。
?? (5)改變各次諧波的相位延遲角度(0~360度),重新測量,觀察波形和頻譜有無改變。
??????????????? ???????????????? ?? ?
????????????????????????????????????????????? ?? 圖12??? 任意波形和組合波形界面
圖13? 組合波形的頻譜
六、思考和練習題
?? 1.為什么組合波形各分量的相位改變,波形會發生變化,但幅度頻譜不變?
?? 2.數據采集的采樣頻率對頻譜測量有什么影響?
 電子發燒友App
電子發燒友App





























評論