前言
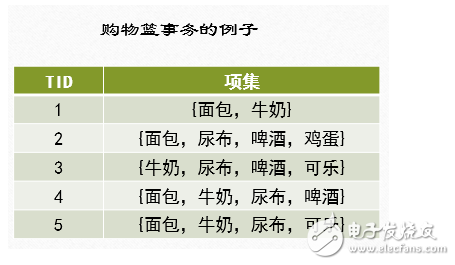
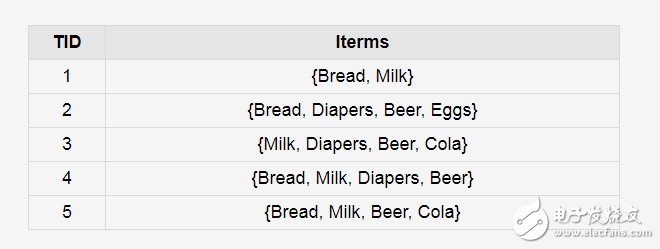
關聯規則挖掘發現大量數據中項集之間有趣的關聯或者相互聯系。關聯規則挖掘的一個典型例子就是購物籃分析,該過程通過發現顧客放入其購物籃中不同商品之間的聯系,分析出顧客的購買習慣,通過了解哪些商品頻繁地被顧客同時買入,能夠幫助零售商制定合理的營銷策略。購物籃事務的例子如下圖所示:??
例如:在同一次去超級市場時,如果顧客購買牛奶,同時他也購買面包的可能性有多大?
通過幫助零售商有選擇地經銷和安排貨架,這種信息會引導銷售。零售商有兩種方法可以進行安排貨架,第一種方法是將牛奶和面包盡可能的放的近一些,方便顧客自取,第二種方法是將牛奶和面包放的遠一些,顧客在購買這兩件物品的時候,這中間貨架上的物品也會被顧客選擇購買。這兩種方法都可以進一步刺激消費。但是,如何發現牛奶和面包之間的關聯關系呢?Apriori算法可以進行關聯規則挖掘。
算法中的基本概念
1、項集和K-項集
令I={i1,i2,i3……id}是購物籃數據中所有項的集合,而T={t1,t2,t3….tN}是所有事務的集合,每個事務ti包含的項集都是I的子集。在關聯分析中,包含0個或多個項的集合稱為項集。如果一個項集包含K個項,則稱它為K-項集。空集是指不包含任何項的項集。例如,在購物籃事務的例子中,{啤酒,尿布,牛奶}是一個3-項集。
2、支持度計數
項集的一個重要性質是它的支持度計數,即包含特定項集的事務個數,數學上,項集X的支持度計數σ(X)可以表示為
σ(X)=|{ti|X?ti,ti∈T}|
其中,符號|*|表示集合中元素的個數。
在購物籃事務的例子中,項集{啤酒,尿布,牛奶}的支持度計數為2,因為只有3和4兩個事務中同時包含這3個項。
3、關聯規則
關聯規則是形如X→Y的蘊含表達式,其中X和Y是不相交的項集,即X∩Y=?。
關聯規則的強度可以用它的支持度(support)和置信度(confidence)來度量。支持度確定規則可以用于給定數據集的頻繁程度,而置信度確定Y在包含X的事務中出現的頻繁程度。
支持度(s)和置信度(c)這兩種度量的形式定義如下:
s(X→Y)=σ(X∪Y)/N
c(X→Y)=σ(X∪Y)/σ(X)
其中, σ(X∪Y)是(X∪Y)的支持度計數,N為事務總數,σ(X)是X的支持度計數。
Example
在購物籃事務的例子中,考慮規則{牛奶,尿布}→{啤酒}。由于項集{牛奶,尿布,啤酒}的支持度計數為2,而事務的總數為5,所以規則的支持度為2/5=0.4。
規則的置信度是項集{牛奶,尿布,啤酒}的支持度計數與項集{牛奶,尿布}支持度技術的商,由于存在3個事務同時包含牛奶和尿布,所以規則的置信度為2/3=0.67。
關聯規則發現
給定事務的集合T,關聯規則發現是指找出支持度大于等于minsup (最小支持度)并且置信度大于等于minconf(最小置信度)的所有規則,minsup和minconf是對應的支持度和置信度閾值。
關聯規則的挖掘是一個兩步的過程:
(1)頻繁項集產生:其目標是發現滿足最小支持度閾值的所有項集(至少和預定義的最小支持計數一樣),這些項集稱作頻繁項集。
(2)規則的產生:其目標是從上一步發現的頻繁項集中提取所有高置信度的規則,這些規則稱作強規則。(必須滿足最小支持度和最小置信度)
Apriori算法介紹
Apriori算法的實質使用候選項集找頻繁項集。
Apriori 算法是一種最有影響的挖掘布爾關聯規則頻繁項集的算法。算法的名字基于這樣的事實:算法使用頻繁項集性質的先驗知識, 正如我們將看到的。Apriori 使用一種稱作逐層搜索的迭代方法,k-項集用于探索(k+1)-項集。首先,找出頻繁1-項集的集合。該集合記作L1。L1 用于找頻繁2-項集的集合L2,而L2 用于找L3,如此下去,直到不能找到頻繁k-項集。找每個Lk 需要一次數據庫掃描。
Apriori性質
Apriori性質:頻繁項集的所有非空子集都必須也是頻繁的。 Apriori 性質基于如下觀察:根據定義,如果項集I不滿足最小支持度閾值s,則I不是頻繁的,即P(I)《 s。如果項A添加到I,則結果項集(即I∪A)不可能比I更頻繁出現。因此, I∪A也不是頻繁的,即 P(I∪A)《 s 。
該性質屬于一種特殊的分類,稱作反單調,意指如果一個集合不能通過測試,則它的所有超集也都不能通過相同的測試。稱它為反單調的,因為在通不過測試的意義下,該性質是單調的。
先驗定理
先驗定理:如果一個項集是頻繁的,則它的所有子集一定也是頻繁的。
(關于先驗定理、單調與反單調可以參考下面的例子理解)
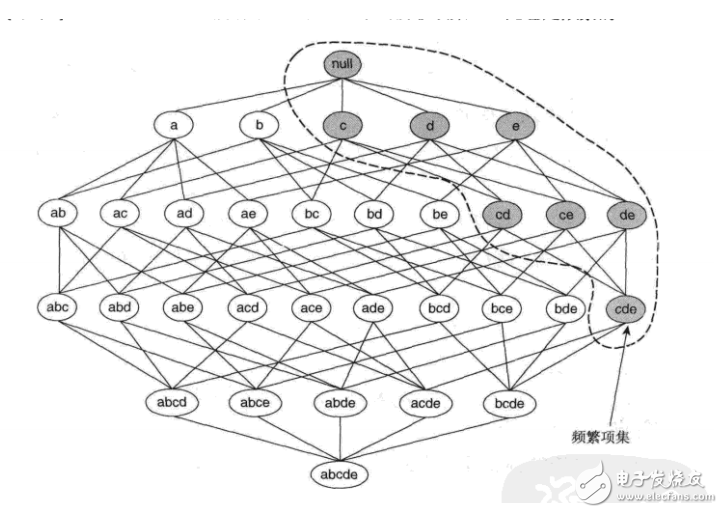
如圖所示,假定{c,d,e}是頻繁項集。顯而易見,任何包含項集{c,d,e}的事務一定包含它的子集{c,d},{c,e},{d,e},{c},5vgeo944t和{e}。這樣,如果{c,d,e}是頻繁的,則它的所有子集一定也是頻繁的。
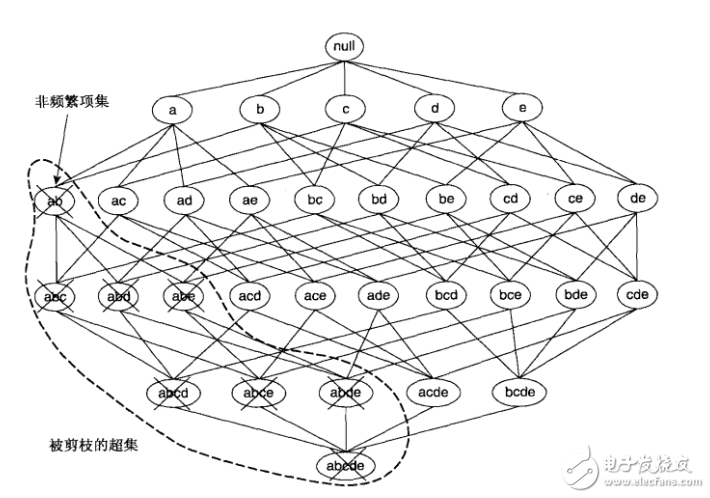
如果項集{a,b}是非頻繁的,則它的所有超集也一定是非頻繁的。即一旦發現{a,b}是非頻繁的,則整個包含{a,b}超集的子圖可以被立即剪枝。這種基于支持度度量修剪指數搜索空間的策略稱為基于支持度的剪枝。
這種剪枝策略依賴于支持度度量的一個關鍵性質,即一個項集的支持度絕不會超過它的子集的支持度。這個性質也稱支持度度量的反單調性。
挖掘頻繁項集
Apriori算法的關鍵是如何用Lk-1找Lk?由下面的兩步過程連接和剪枝組成。
連接步:為找Lk,通過Lk-1與自己連接產生候選k-項集的集合。該候選項集的集合記作Ck。設l1和l2是Lk-1中的項集。記號li[j]表示li的第j項(例如,l1[k-2]表示l1的倒數第3項)。為方便計,假定事務或項集中的項按字典次序排序。執行連接Lk-1 Lk-1;其中,Lk-1的元素是可連接的,如果它們前(k-2)個項相同;即,Lk-1的元素l1和l2是可連接的,如果(l1[1]=l2[1])∧(l1[2]=l2[2])∧…∧(l1[k-2]=l2[k-2])∧(l1[k-1]《 l2[k-1])。條件(l1[k-1]《 l2[k-1])是簡單地保證不產生重復。連接l1和l2產生的結果項集是l1[1]l1[2]…l1[k-1]l2[k-1]。
剪枝步:Ck是Lk的超集;即,它的成員可以是頻繁的,也可以不是頻繁的,但所有的頻繁k-項集都包含在Ck中。掃描數據庫,確定Ck中每個候選的計數,從而確定Lk(即,根據定義,計數值不小于最小支持度計數的所有候選是頻繁的,從而屬于Lk)。然而,Ck可能很大,這樣所涉及的計算量就很大。為壓縮Ck,可以用以下辦法使用Apriori性質:任何非頻繁的(k-1)-項集都不是可能是頻繁k-項集的子集。因此,如果一個候選k-項集的(k-1)-子集不在Lk-1中,則該候選也不可能是頻繁的,從而可以由Ck中刪除。這種子集測試可以使用所有頻繁項集的散列樹快速完成。
Apriori算法
算法6.2.1(Apriori) 使用逐層迭代找出頻繁項集
輸入:事務數據庫D;12345678910111213141516最小支持度閾值。
輸出:D中的頻繁項集L。
方法:
1) L1 = find_frequent_1_itemsets(D); //找出頻繁1-項集的集合L1
2) for(k = 2; Lk-1 ≠ ?; k++) { //產生候選,并剪枝
3) Ck = aproiri_gen(Lk-1,min_sup);
4) for each transaction t∈D{ //掃描D進行候選計數
5) Ct = subset(Ck,t); //得到t的子集
6) for each candidate c∈Ct
7) c.count++; //支持度計數
8) }
9) Lk={c∈Ck| c.count ≥min_sup} //返回候選項集中不小于最小支持度的項集
10) }
11) return L = ∪kLk;//所有的頻繁集
第一步(連接 join)
Procedure apriori_gen(Lk-1: frequent (k-1)-itemset; min_sup: support)
1) for each itemset l1∈Lk-1
2) for each itemset l2∈Lk-1
3) if(l1[1]=l2[1])∧。..∧(l1[k-2]=l2[k-2])∧(l1[k-1]《l2[k-1]) then{
4) c = l1 l2; //連接步:l1連接l2
//連接步產生候選,若K-1項集中已經存在子集c,則進行剪枝
5) if has_infrequent_subset(c,Lk-1) then
6) delete c; //剪枝步:刪除非頻繁候選
7) else add c to Ck;
8) }
9) return Ck;
12345678910111213
第二步:剪枝(prune)
Procedure has_infrequent_subset(c:candidate k-itemset; Lk-1:frequent (k-1)-itemset) //使用先驗定理
1) for each (k-1)-subset s of c
2) if c?Lk-1 then
3) return TRUE;
4) return FALSE;
1234567
由頻繁項集產生關聯規則
一旦由數據庫D中的事務找出頻繁項集,由它們產生強關聯規則是直接了當的(強關聯規則滿足最小支持度和最小置信度)。對于置信度,可以用下式,其中條件概率用項集支持度計數表示。
confidence(A→B)=P(A│B)=support(A∪B)/support(A)
其中,support(A∪B)是(A∪B)的支持度計數,support(A)是A的支持度計數。
根據該式,關聯規則可以產生如下:
? 1、對于每個頻繁項集l,產生l的所有非空子集。
? 2、對于l的每個非空子集s,如果support(l)/support(s) ≥min_conf,則輸出規則“s?(l-s)”。其中,min_conf是最小置信度閾值。
由于規則由頻繁項集產生,每個規則都自動滿足最小支持度。頻繁項集連同它們的支持度預先存放在hash表中,使得它們可以快速被訪問。
Apriori算法的實例
問題:數據庫中有9個事務,即|D| = 9。Apriori假定事務中的項按字典次序存放。我們使用下圖解釋Apriori算法發現D中的頻繁項集。 圖四
分析與解:
(一)、挖掘頻繁項集
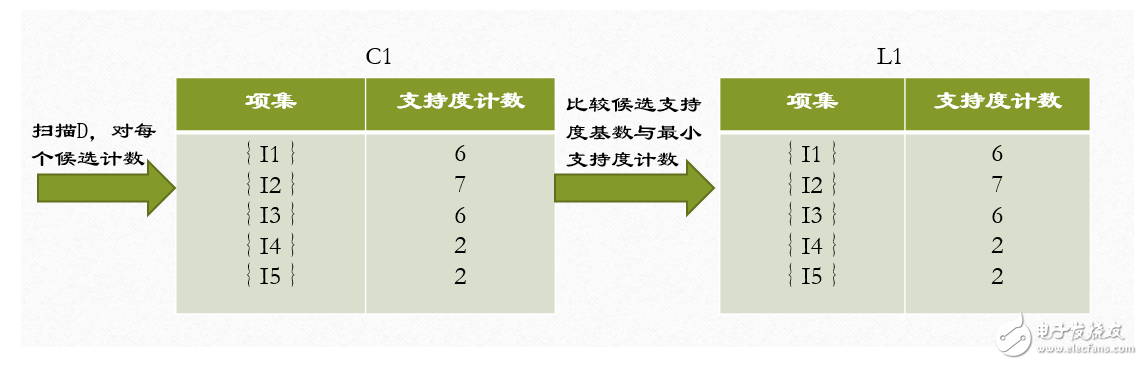
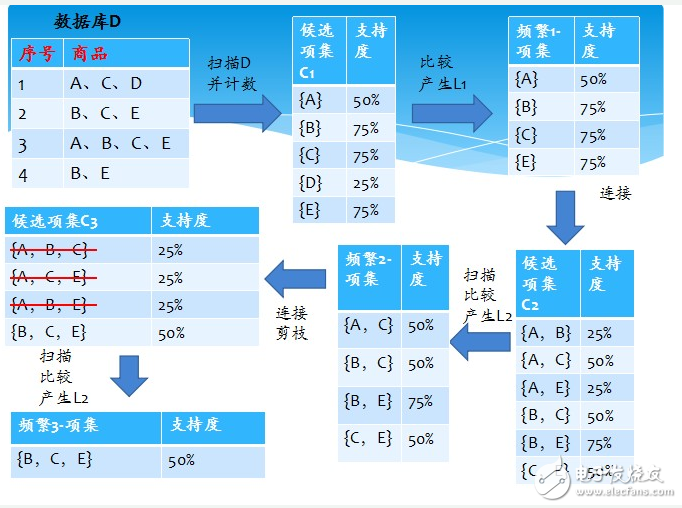
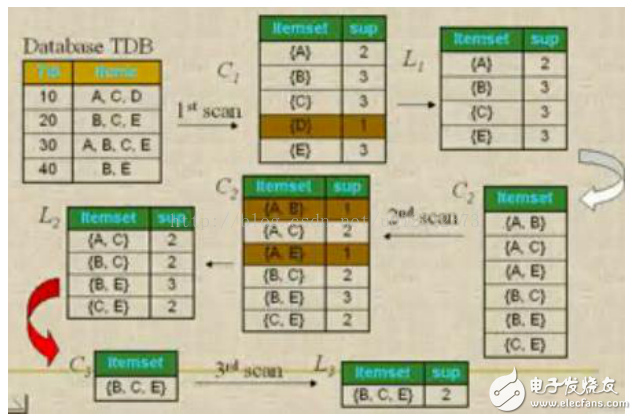
1、在算法的第一次迭代,每個項都是候選1-項集的集合C1的成員,算法簡單地掃描所有的事務,對每個項的出現次數計數。
2、假定最小事務支持計數為2(即,minsup=2/9=22%)。可以確定頻繁1-項集的集合L1。它由具有最小支持度的候選1-項集組成。
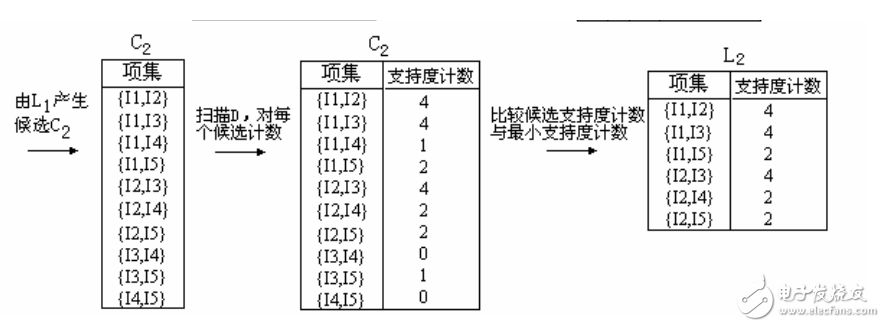
3、為發現頻繁2-項集的集合L2,算法使用L1 L1產生候選2-項集的集合C2。
4、下一步,掃描D中事務,計算C2中每個候選項集的支持計數。
5、確定頻繁2-項集的集合L2,它由具有最小支持度的C2中的候選2-項集組成。
【注】 L1 L1等價于L1×L1,因為Lk Lk的定義要求兩個連接的項集共享k-1個項。
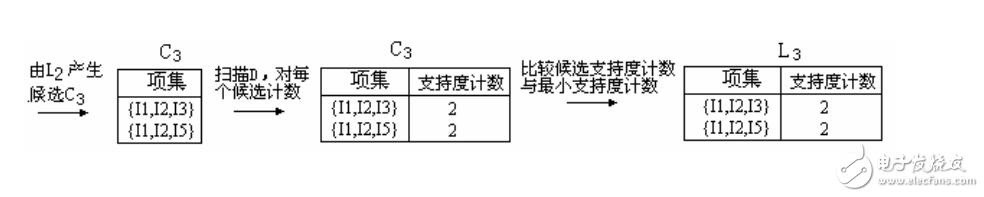
6、候選3-項集的集合C3的產生詳細地列在圖中。首先,令C3 = L2 L2 = {{I1,I2,I3}, {I1,I2,I5}, {I1,I3,I5}, {I2,I3,I4}, {I2,I3,I5}, {I2,I4,I5}}。根據Apriori性質,頻繁項集的所有子集必須是頻繁的,我們可以確定后4個候選不可能是頻繁的。因此,我們把它們由C3刪除,這樣,在此后掃描D確定L3時就不必再求它們的計數值。注意,Apriori算法使用逐層搜索技術,給定k-項集,我們只需要檢查它們的(k-1)-子集是否頻繁。
【L2 L2連接生成C3的過程】
1.連接:C3= L2 L2={{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}} {{I1,I2},{I1,I3},{I1,I5},{I2,I3},{I2,I4},{I2,I5}} = {{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}
2.使用Apriori性質剪枝:頻繁項集的所有子集必須是頻繁的。存在候選項集,其子集不是頻繁的嗎?
?{I1,I2,I3}的2-項子集是{I1,I2},{I1,I3}和{I2,I3}。{I1,I2,I3}的所有2-項子集都是L2的元素。因此,保留{I1,I2,I3}在C3中。
?{I1,I2,I5}的2-項子集是{I1,I2},{I1,I5}和{I2,I5}。{I1,I2,I5}的所有2-項子集都是L2的元素。因此,保留{I1,I2,I5}在C3中。
?{I1,I3,I5}的2-項子集是{I1,I3},{I1,I5}和{I3,I5}。{I3,I5}不是L2的元素,因而不是頻繁的。這樣,由C3中刪除{I1,I3,I5}。
?{I2,I3,I4}的2-項子集是{I2,I3},{I2,I4}和{I3,I4}。{I3,I4}不是L2的元素,因而不是頻繁的。這樣,由C3中刪除{I2,I3,I4}。
?{I2,I3,I5}的2-項子集是{I2,I3},{I2,I5}和{I3,I5}。{I3,I5}不是L2的元素,因而不是頻繁的。這樣,由C3中刪除{I2,I3,I5}。
?{I2,I4,I5}的2-項子集是{I2,I4},{I2,I5}和{I4,I5}。{I4,I5}不是L2的元素,因而不是頻繁的。這樣,由C3中刪除{I2,I3,I5}。
3.這樣,剪枝后C3 = {{I1,I2,I3},{I1,I2,I5}}
7、掃描D中事務,以確定L3,它由具有最小支持度的C3中的候選3-項集組成。
8、算法使用L3 L3產生候選4-項集的集合C4。盡管連接產生結果{{I1,I2,I3,I5}},這個項集被剪去,因為它的子集{I1,I3,I5}不是頻繁的。這樣,C4=?,因此算法終止,找出了所有的頻繁項集。
(二)、由頻繁項集產生關聯規則
假定數據包含頻繁項集l={I1,I2,I5},可以由l產生哪些關聯規則?l的非空子集有{I1,I2},{I1,I5},{I2,I5},{I1},{I2}和{I5}。結果關聯規則如下,每個都列出置信度。
I1∩I2→I5, confidence=2/4=0.5=50%
I1∩I5→I2, confidence=2/2=1=100%
I2∩I5→I1, confidence=2/2=1=100%
I1→I2∩I5, confidence=2/6=0.33=33%
I2→I1∩I5, confidence=2/7=0.29=29%
I5→I1∩I2, confidence=2/2=1=100%
如果最小置信度閾值為70%,則只有2、3和最后一個規則可以輸出,因為只有這些才是強規則。
優缺點
優點
使用先驗性質,大大提高了頻繁項集逐層產生的效率;簡單易理解;數據集要求低。
缺點
1、候選頻繁K項集數量巨大。
2、在驗證候選頻繁K項集的時候,需要對整個數據庫進行掃描,非常耗時。
改進算法
算法思想:
上面的原始算法中由Ck(Lk-1直接生成的)到Lk經過了兩步處理,第一步根據Lk-1進行裁剪,第二步根據minsupport裁剪。上面提到的兩個提高效率的方法都是基于第一步的。當經過聯接生成K維數據項集時,判斷它的K-1維子集是否存在于Lk-1中,如果不在直接刪除。這樣每生成一個K維數據項集時,就要搜索一遍Lk-1。改進算法的思想就是只需要搜索一遍Lk-1就可以了。當所有聯接完成的時候,掃描一遍Lk-1,對于Lk-1任意元素A,判斷A是否為Ck中元素 c的子集,如果是,對子集c進行計數。也就是統計Lk-1中包含Ck中任意元素c的K-1維子集的個數。最后根據c進行裁剪。c的計數,即 Lk-1中包含的c的子集的個數,小于K,則刪除。
改進算法偽代碼
算法的主體不變,aprriori_gen函數改變如下,函數 has_infrequent_subset不再需要。
procedure apriori_gen(Lk-1:frequent(k-1)-itemsets;minsupport:minimum support threshold)
(1)for each itemset l1 ∈ Lk-1
(2)for each itemset l2∈ L k-1
(3)if(l1[1]=l2[1])∧(l1[2]=l2[2])∧…∧(l1[k-2]=l2[k-2])∧(l1[k-1]=l2[k-1]) then
(4)c=l1∪ l2;
(5)for each itemset l1∈ L k-1 //掃描Lk-1中的元素
(6)for each candidate c∈ Ck //掃描 Ck中的元素
(7)if l1 is the subset of Ck then //判斷前者是不是后者的子集,如果是計數加1
(8)c.number++;
(9)C‘k={ c∈Ck |c.number=k};
(10)return C’k;
12345678910111213
例子對比:
問題:假設Lk-1={{1,2,3},{1,2,4},{2,3,4},{2,3,5},{1,3,4}},求Lk。
由Lk-1得到Ck={{1,2,3,4},{2,3,4,5},{1,2,3,5}}。
原算法:首先得到{1,2,3,4}的子集{1,2,3},{1,2,4},{2,3,4},{1,3,4}。然后判斷這些子集是不是 Lk-1的元素。如果都是則保留,否則刪除。這里保留,{2,3,4,5}和{1,2,3,5}則應該刪除。得到C’k={{1,2,3,4}}。
改進算法:首先從Lk-1中取元素{1,2,3},掃描Ck中的元素,看{1,2,3}是不是Ck元中元素的子集,{1,2,3}是{1,2,3,4}的子集,{1,2,3,4}的計數加1,{1,2,3}不是{2,3,4,5}的子集,計數不變,是{1,2,3,5}的子集,計數加1,經過對{1,2,3}處理后得到計數{1,0,1};然后看{1,2,4},{1,2,4}是{1,2,3,4}的子集,而不是 {2,3,4,5}的子集,也不是{1,2,3,5}的子集,計數不變,計數變為{2,0,1};考察{2,3,4},{2,3,4}是{1,2,3,4}的子集,也是{2,3,4,5}的子集,不是{1,2,3,5}的子集,計數變為{3,1,1};{2,3,5}不是{1,2,3,4}的子集,是{2,3,4,5}的子集,也是{1,2,3,5}的子集,計數變為{3,2,2};{1,3,4}是{1,2,3,4}的子集,不是{2,3,4,5}的子集,也不是{1,2,3,5}的子集,計數變為{4,2,2}。對數據掃描完畢。此時K=4,只有第一個元素的計數為4,為高頻數據項集。得到C’k={{1,2,3,4}}。
復雜度對比
下面對原算法和改進算法的性能進行比較。Lk-1中的數據項集的個數記為|Lk-1|,Ck中的數據項集的個數記為|Ck|,Ck中元素的子集個數設為ni,其中i=1~|Ck| 。這里只分析從Ck~C’k的處理。原 算法從 AprioriCk中取元素,然后求該元素的子集,判斷該子集是否在 |Ck|中。需要進行的計算為? 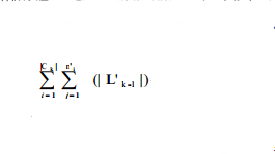 次, 1<=|L’k-1|<=|L’k-1|,1<= n’i <=n i。而改進算法是從Lk-1中選取元素,看是不是Ck中元素的子集,對 Ck中數據項集的子集個數進行統計。需要進行的計算是(|Lk-1|+1)*|Ck| 次。如果 n’i =1,就是每次只取Ck中數據項集的一個子集就可以判斷該數據項集,則兩個算法的效率基本相同,但是這種情況很少出現,從而大部分情況下,改進算法的效率要高于原算法。
次, 1<=|L’k-1|<=|L’k-1|,1<= n’i <=n i。而改進算法是從Lk-1中選取元素,看是不是Ck中元素的子集,對 Ck中數據項集的子集個數進行統計。需要進行的計算是(|Lk-1|+1)*|Ck| 次。如果 n’i =1,就是每次只取Ck中數據項集的一個子集就可以判斷該數據項集,則兩個算法的效率基本相同,但是這種情況很少出現,從而大部分情況下,改進算法的效率要高于原算法。
 電子發燒友App
電子發燒友App











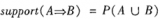










評論