實驗三、戴維南定理和諾頓定理實驗
一、 實驗?zāi)康?/font>
1、 通過對戴維南定理和諾頓定理的實驗驗證,加深對等效電路概念的理解。
⒉ 學(xué)會幾種測量電源內(nèi)阻以及開路電壓的方法。
3、學(xué)會用補(bǔ)償法測量含源一端口網(wǎng)絡(luò)等效參數(shù)。
二、實驗原理
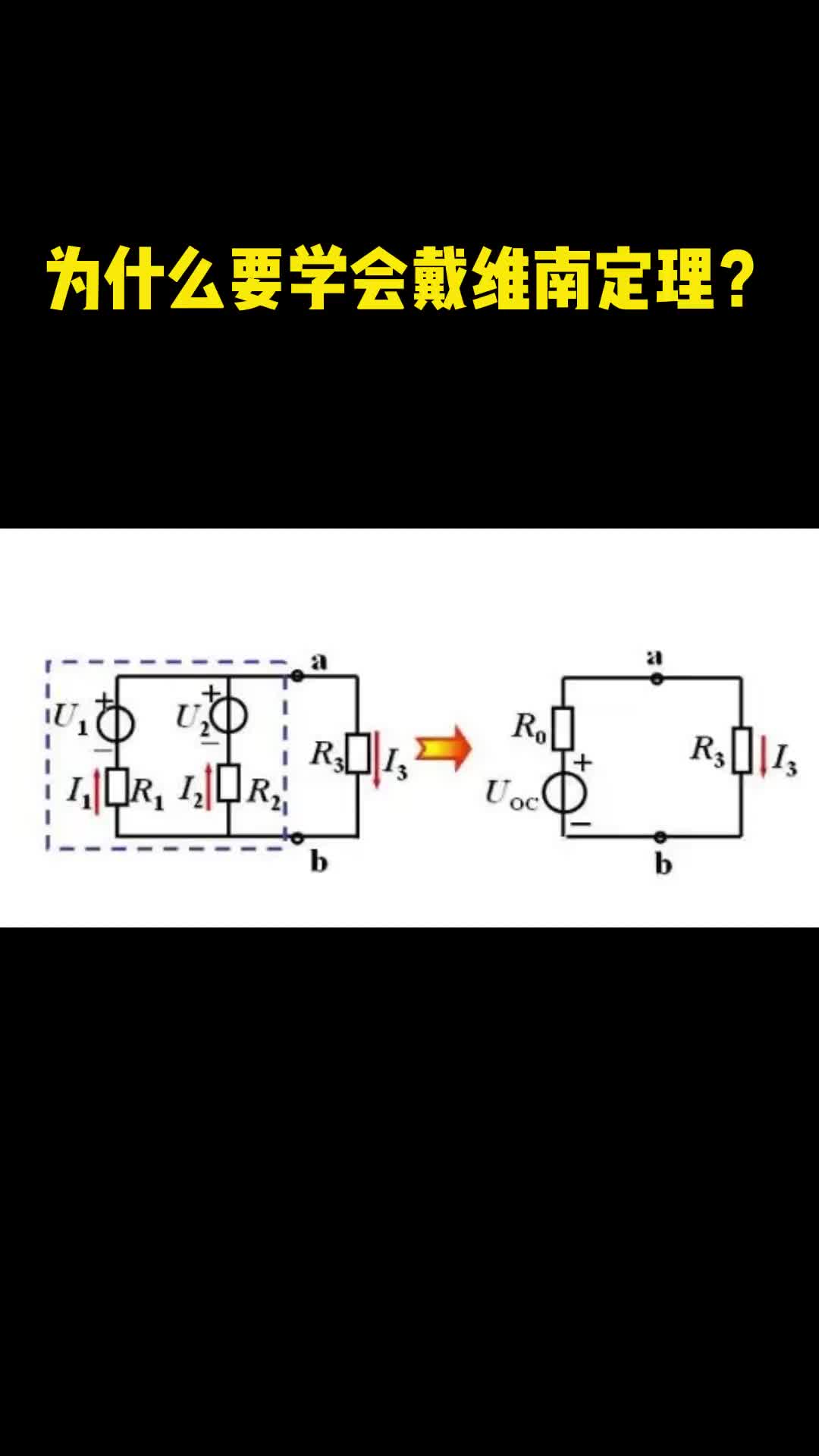
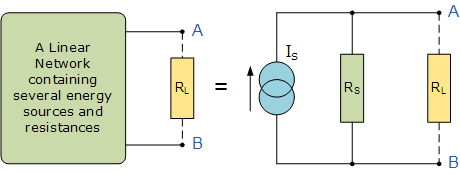
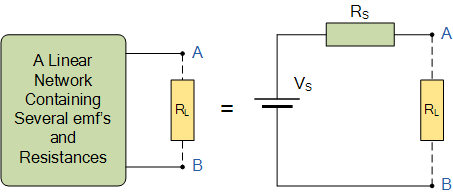
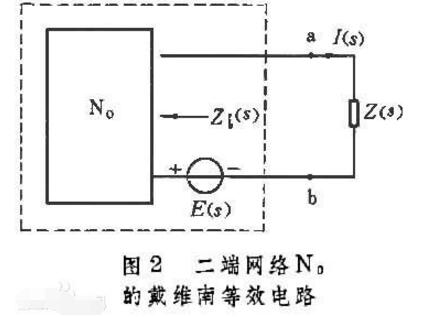
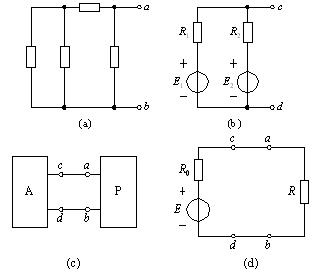
根據(jù)戴維南定理,任何一個線性含源一端口網(wǎng)絡(luò),它的外部特性,總可以等效為理想電壓源Uoc和電阻Rs的串聯(lián)組合支路。Uoc為原網(wǎng)絡(luò)開路電壓,Rs為原網(wǎng)絡(luò)去源后的端口處的入端電阻,如圖3-1所示。
任何一個線性含源一端口網(wǎng)絡(luò),根據(jù)諾頓定理,它的外部特性,總可以等
效為理想電流源Isc和一電導(dǎo)Gs的并聯(lián)組合。Isc為原網(wǎng)絡(luò)的短路電流,Gs為原
網(wǎng)絡(luò)去源后端口處的入端電導(dǎo)。
如圖3-2所示。
戴維南定理和諾頓定理是兩個完全獨(dú)
立的定理,盡管兩定理所述等效電路之間存在對偶形式,且有
Uoc=IscRs Gs=1/Rs 的關(guān)系。
電路的等效性在于變換前后原電路和等效電路的外部特性保持不變。即端口
CD 處的電壓和端口電流保持不變。在滿足這一前提下,含源一端口網(wǎng)絡(luò)戴維南
等效電路的Uoc和Rs 以及諾頓等效電路的Isc和Gs被稱為含源一端口網(wǎng)絡(luò)的
等效參數(shù)。等效參數(shù)的測量是將含源一端網(wǎng)絡(luò)等效為戴維南電路和諾頓電路的關(guān)
鍵。
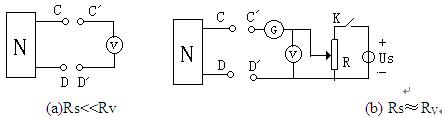
關(guān)于含源一端口網(wǎng)絡(luò)開路電壓Uoc的測量:常用方法有兩種,直接測量法和
補(bǔ)償法。
1、直接測量法:
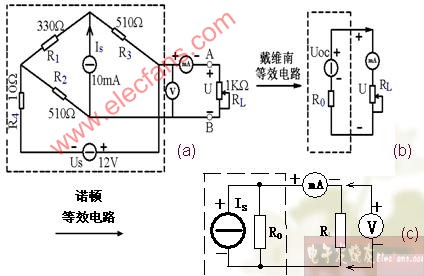
當(dāng)含源一端口網(wǎng)絡(luò)去源后的入端電阻Rs與電壓表內(nèi)阻Rv相比,Rs<<Rv, 即
Rs相對于Rv可以忽略不計時,可以直接用電壓表測量開路電壓。如圖3-3(a)所
示,電壓表讀數(shù)即是含源一口網(wǎng)絡(luò)的開路電壓Uoc。
2、補(bǔ)償法:
當(dāng)含源一端口網(wǎng)絡(luò)去源后的入端電阻Rs與電壓表內(nèi)阻Rv相比較,不可忽
略時,用電壓表直接測量開路電壓,會影響被測電路的原工作狀態(tài),使所測電壓
與實際值之間有較大誤差。這時用補(bǔ)償法可以排除電壓表內(nèi)阻Rv對測量所造成
的影響。
圖4-3(b)是用補(bǔ)償法測量開路電壓的電路圖,測量步驟如下:
先將補(bǔ)償電路中開關(guān)K開啟,將C’D’與CD對應(yīng)相接,調(diào)整補(bǔ)償電路中分
壓器的輸出電壓,使它近似等于用電壓表直接測量閉合回路電壓。再閉合開關(guān)K,
細(xì)調(diào)補(bǔ)償電路中分壓器的輸出電壓,待檢流計中無電流通過即指針指示為零。此
時電壓表讀數(shù)即是被測電源一端口開路電壓Uoc。由于檢流計中無電流,相當(dāng)于
CD開路,補(bǔ)償電流的接入,沒有影響一端口的工作狀態(tài)。
(a)Rs<<Rv (b) Rs≈RV
 r
r
圖 3-3
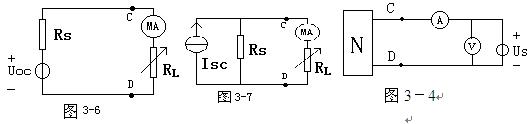
含源一端口網(wǎng)絡(luò)入端等效電阻Rs的求法:
比較簡單的含源一端口網(wǎng)絡(luò)入端電阻,可將網(wǎng)絡(luò)中電壓源短路,電流源開路
(去源)后,根據(jù)網(wǎng)絡(luò)中電阻的串并聯(lián)組合,通過計算求得Rs。
比較復(fù)雜的含源一端口網(wǎng)絡(luò),很難通過計算求得入端電阻。亦可通過測量(直
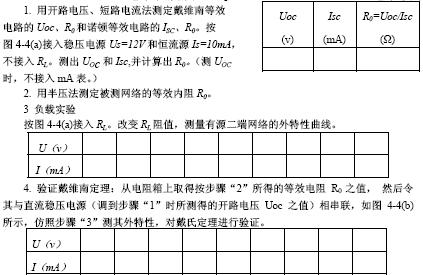
接法、補(bǔ)償法)含源一端口網(wǎng)絡(luò)的開路電壓Uoc和短路電流Isc,則Rs=Uoc/Isc
對于復(fù)雜含源一端口網(wǎng)絡(luò)還可以將網(wǎng)絡(luò)去源后,在端口處加一電壓源U,按圖
3-4接線,用電壓表和電流表測無源一端口網(wǎng)絡(luò)端口處的電壓U和電流I,則Rs=U/I
三、實驗儀器及設(shè)備
直流穩(wěn)壓穩(wěn)流源 一臺
直流毫安表 一塊
數(shù)字萬用表表 一塊
ZH-12通用電學(xué)實驗臺
檢流計 (或直流微安表) 一塊
電阻 五只
電位器 一只
導(dǎo)線若干
四、實驗內(nèi)容與步驟
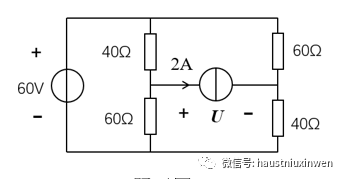
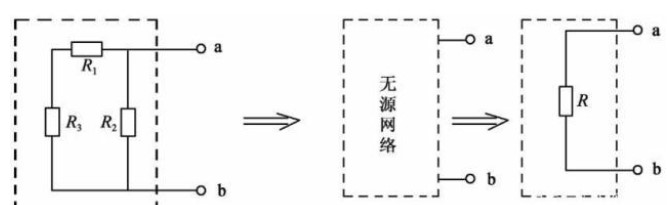
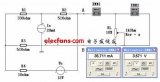
1、 在ZH-12通用電學(xué)實驗臺上按圖3-5接線,U1=25V,C,D左側(cè)用虛線
框起部分為含源一端口網(wǎng)絡(luò)。
2、測量含源一端口網(wǎng)絡(luò)的外部特性:將S1、S2閉合,調(diào)節(jié)外接電阻RL,使其分別為表3-1中所列數(shù)值,記錄通過R2電流(即RL中電流,X5,X6接口處毫安表讀數(shù))和C、D間電壓填入表3-1中。
表3-1
|
RL(Ω) |
0 |
500 |
1k |
1.5k |
2k |
2.5k |
開路 |
|
I(mA) |
|
|
|
|
|
|
|
|
U(V) |
|
|
|
|
|
|
|
3、步驟2中RL=0的電流(短路電流Isc)和開路電壓(此電壓在步驟2中采用直接測量法測得)Uoc代入公式Rs=RCD=Uoc/Isc
求出Rs
4、再用補(bǔ)償法重作步驟3,測量Uoc Rs=RCD=Uoc/Isc
5、 將Uoc用直流穩(wěn)壓電源代替,調(diào)節(jié)直流穩(wěn)壓電源輸出電壓為Uoc,與Rs
串聯(lián)組成戴維南等效電路如圖3-6,調(diào)節(jié)RL,使其分別為表3-1中數(shù)值,測量RL
電流和CD間電壓,填入表3-2中。比較表3-1和表3-2數(shù)據(jù),驗證戴維南定理。
表3-2
|
RL(Ω) |
0 |
500 |
1 k |
1.5 k |
2k |
2.5k |
開路 |
|
I(mA) |
|
|
|
|
|
|
|
|
U(V) |
|
|
|
|
|
|
|
6、將步驟1中RL=0的短路電流Isc用恒流源替代,調(diào)節(jié)恒流源的輸出電流等于Isc,
與Rs并聯(lián)構(gòu)成諾頓等效電路,如圖3-7所示。調(diào)節(jié)RL使其分別為表3-3中數(shù)值,測量RL中
電流和CD間電壓,填入表3-3中,比較表3-1和表3-3中數(shù)據(jù)以驗證諾頓定理。
表3-3
|
RL(Ω) |
0 |
500 |
1 k |
1.5 k |
2k |
2.5 k |
開路 |
|
I(mA) |
|
|
|
|
|
|
|
|
U(V) |
|
|
|
|
|
|
|
五、實驗報告
在同一張坐標(biāo)紙上畫出原一端口網(wǎng)絡(luò)和各等效網(wǎng)絡(luò)的伏安特性曲線,并做分析比
較,說明如何驗證戴維南定理和諾頓定理.
 電子發(fā)燒友App
電子發(fā)燒友App





































評論