RLC串聯電路暫態特性的研究
電阻、電容及電感是電路中的基本元件, 在交流電路中,電阻值和頻率無關,電容具有 “ 通高頻、阻低頻 ” 的特性 , 電感具有 “ 通低頻,阻高頻 ” 的特性 . 由 RC 、 RL 、 RLC 構成的串聯電路具有不同的特性,包括暫態特性、穩態特性、諧振特性.它們在電子電路中有許多用途.本實驗主要研究 RC 、 RL 、 RLC 電路的暫態特性 .?
【預習要求】
1. 閱讀大學物理中有關 RL 、 RC 、 RLC 電路的特點 .
2. 復習示波器實驗 .
?
【實驗目的】
?
1 .學習如何通過實驗方法研究有關 RC 、 RL 和 RLC 串聯電路的暫態過程 .
2 .通過研究 RC 、 RL 和 RLC 串聯電路的暫態過程,加深對電容充、放電規律,電感的電磁感應特性及振蕩回路特點的認識 .
?
【實驗儀器】
?
信號發生器,雙蹤示波器,電阻箱, RLC 電路板
?
【實驗要求】
?
1 .取不同參數的 RC 或 RL 組成串聯電路,測量并描繪當時間常數小于或大于方波的半周期時的電容或電感上的波形,計算時間常數并與理論值比較;
2 .選擇不同的 RLC 組成的串聯電路,測量并描繪欠阻尼過程、臨界阻尼過程、過阻尼過程時電容上的波形,計算時間常數并與理論值比較.
?
【實驗提示】
?
一、原理設計
1 . RC 串聯電路的暫態過程
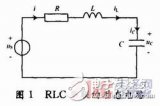
在由 R 、 C 組成的電路中,暫態過程是電容的充放電過程.圖 29-1 為 RC 串聯電路 .其中信號源用方波信號. 在上半個周期內,方波電壓為 + E ,其對電容充電;在下半個周期內,方波電壓為零,電容對地放電.充電過程中的回路方程為
( 29-1 )
由初始條件 t = 0 時, U C = 0 ,得解為
( 29-2 )
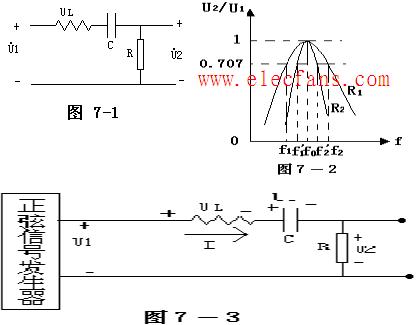
從 U C 、 U R 二式可見, U C 是隨時間 t 按指數函數規律增長,而電阻電壓 U R 隨時間 t 按指數函數規律衰減,如 圖 29-2 中 U – t 、 U C – t 及 U R – t 曲線 所示.
在放電過程中的回路方程為
( 29-3 )
由初始條件 t = 0 時, U C = E ,得解為
( 29-4 )
從 U C 、 U R 式可見,它們都隨時間 t 按指數函數規律衰減.式中的 RC = t 具有時間的量綱,稱為時間常數,是表征暫態過程進行快慢的一個重要物理量.與時間常數 t 有關的另一個另一個表征 RC 電路特征的值為半衰期 T 1/2 ,定義為當 U C ( t )下降到初值(或上升至終值)一半時所需要的時間,它同樣反映了暫態過程的快慢程度,與 t 的關系為
T 1/2 = t ln2 = 0.693 t (或 t = 1.443 T 1/2 ) ( 29-5 )
2 . RL 串聯電路的暫態過程
與 RC 串聯電路進行類似分析可得, RL 串聯電路的時間常數 t 及半衰期 T 1/2 分別 為:
( 29-6 )
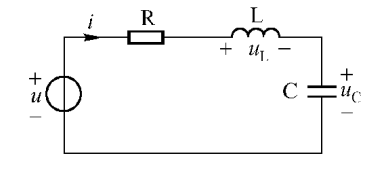
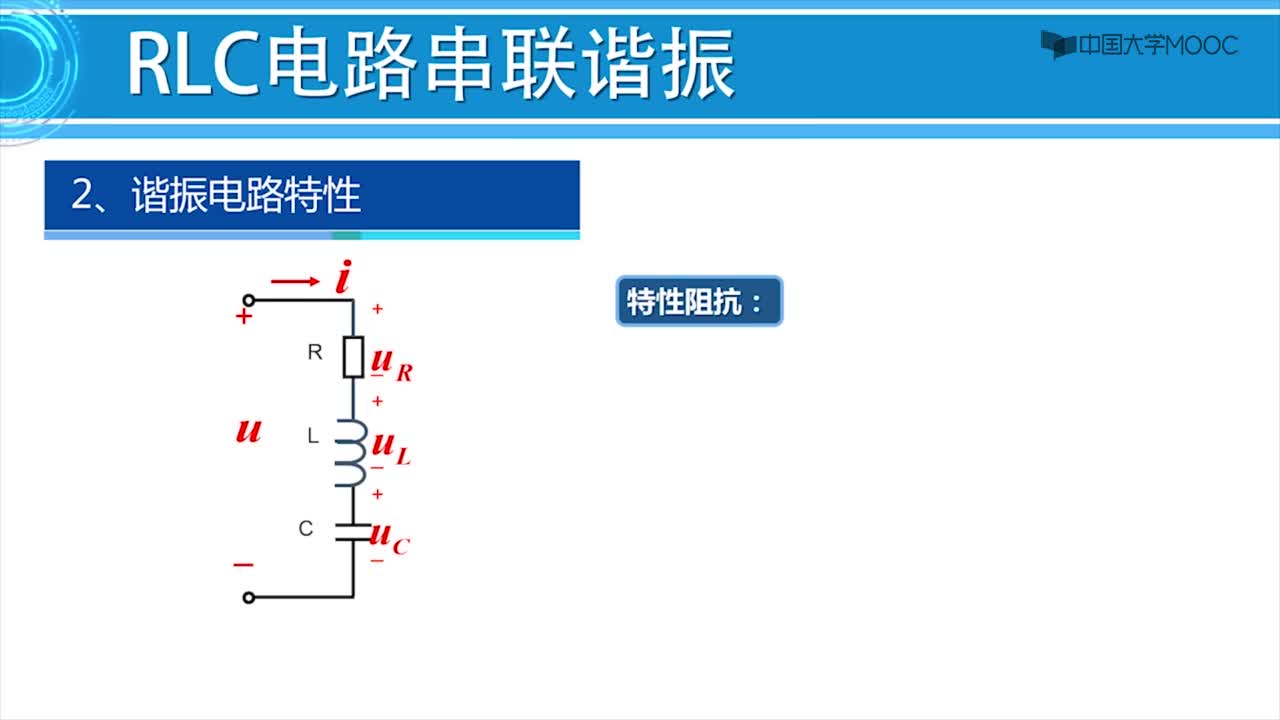
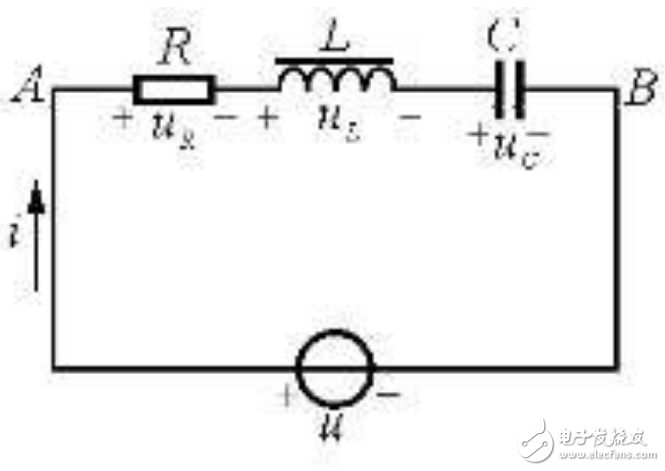
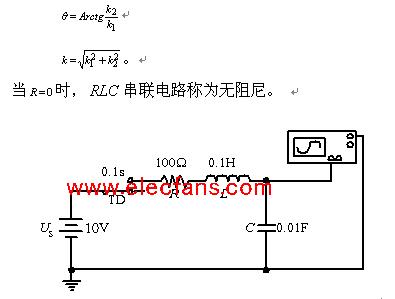
3 . RLC 串聯電路的暫態過程
先討論 RLC 電路中突然接入電源,電容器上電壓滿足的微分方程為
( 29-7 )
等式兩邊同除以 LC ,并令
( 29-8 )
則上式可化為
( 29-9 )
式( 29-9 )為一阻尼振蕩方程, b 為阻尼系數, w 0 為電路的固有頻率.又由本過程的兩個初始條件
; ( 29-10 )
所以( 29-10 )式最終解的形式取決于 b 和 w 0 的相對大小 .
下面就分三種情況給出結果
(1)欠阻尼
當 時,稱為欠阻尼,其解為
( 29-11 )
式中, ,式( 29-11 )稱為阻尼振蕩解.
(2)過阻尼
當 時,稱為 過阻尼. 其解為:
( 29-12 )
式中:
(3)臨界阻尼
當 時,稱為臨界阻尼,此時其解為
( 29-13 )
當電路達到穩定后,突然撤去電源電動勢(即 E = 0 ),電路的變化類似于 充電過程 .方程的解也分為三種情況. 以上討論的充、放電的條件是加階越波且源內阻為零.在實驗中,我們可以用源內阻很小的方波源來代替上述條件.只要方波的周期遠大于電路的時間常數就可以.
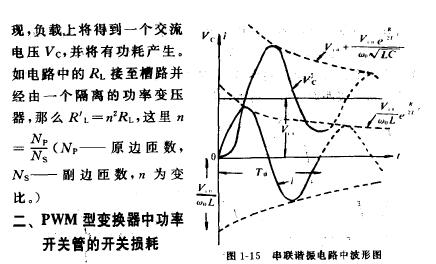
上述三種情況下 U C 隨時間 t 的變化如圖 29-3 所示 .
【如圖所示】
?
【設計報告要求】
?
1. 寫明實驗的目的和意義
2. 闡明實驗原理和設計思路
3. 說明實驗方法和測量方法的選擇
4. 列出所用儀器和材料
5. 確定的實驗步驟
6. 設計數據記錄表格
7. 確定實驗數據的處理方法
?
【注意事項】
1 .應用各種儀器前,仔細查閱有關說明書和使用方法.
2 .各電路元件在測量時,接地點應與儀器的接地點一致.?
【思考題】
?
1 .在 RC 暫態過程中,固定方波的頻率,而改變電阻的阻值,為什么會有不同的波形?而改變方波的頻率,會得到類似的波形嗎?
2 .在 RLC 暫態過程中,若方波的頻率很高或很低,能觀察到阻尼振蕩的波形嗎?如何由阻尼振蕩的波形來測量 RLC 電路的時間常數?
3 .在 RC 、 RL 電路中,當 C 或 L 的損耗電阻不能忽略不計時,能否用本實驗測量電路中時間常數?
?
 電子發燒友App
電子發燒友App



























評論