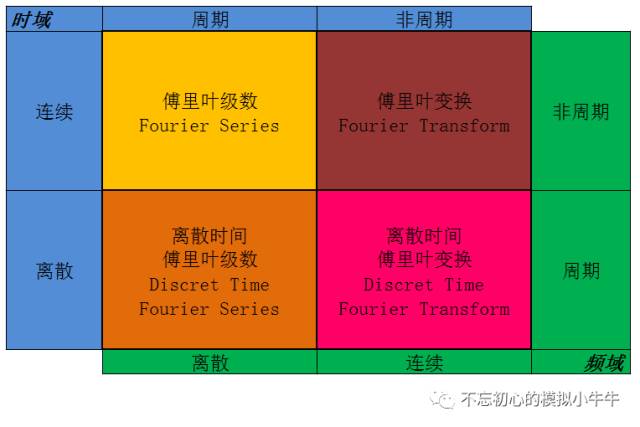
傅氏分析與小波分析

傅氏分析與小波分析
11.1 知識要點 — 傅氏分析與小波分析
11.1.1傅氏分析
???
11.1.2小波分析
11.2 觀察與實驗
11.2.1 信號頻譜分析
xsf11_1.m? (信號生成與顯示程序)
【???? dalt=0.002;? %采樣間隔
t=0:0.002:1.2;????
rn=randn(1,length(t));rn(1:300)=0;??? %產生隨機序列
s=sin(2*pi*10*t)+sin(2*pi*50*t)+rn; %生成模擬信號
save singal1 dalt s;
clear;
load singal1;
t=[0:length(s)-1]*dalt;plot(t,s,'k');Ylabel('幅值');Xlabel('時間');
title('模擬信號'); ???】

???????????
xsf11_2.m (模擬信號singal1的頻譜分析)
【??? clear;load singal1; t=[0:length(s)-1]*dalt;
subplot(211);plot(t,s);? Ylabel('幅值'); Xlabel('時間');title('原始信號');
fs=fft(s,512);????????? %快速傅氏變換
pp=fs.*conj(fs)/512; %計算功率譜
ff=(0:255)/512/dalt; %計算各點對應的頻率值
subplot(212);plot(ff,pp(1:256));? Ylabel('功率譜密度');Xlabel('頻率');
title('信號功率譜');??????? 】
11.2.2 如何得到小波函數
?????? ◆用下面的程序產生并顯示與小波db4相關聯的四個濾波器組。
xsf11_3.m
【? wname='db4';
[LD,HD,LR,HR]=wfilte rs(wname);
subplot(221);stem(LD);title('低通分解濾波器');grid;
subplot(223);stem(LR);title('低通重構濾波器');grid;
subplot(222);stem(HD);title('高通分解濾波器');grid;
subplot(224);stem(HR);title('高通重構濾波器');grid;???? 】
運行結果見圖11.3。
?????? ◆用下面的程序觀察小波函數db4的迭代生成過程。
xsf11_4.m
【? for I=1:10
[phi,psi,xval]=wavefun('sym4',I);
plot(xval,psi+2*I);title('小波函數的生成過程');
hold on
end
hold off 】
???? 結果見圖11.4。
11.2.3單尺度一維離散小波分解與重構
xsf11_5.m（信號singal1的單尺度離散小波分解與重構）
【??? clear;
load singal1;?????????????????????????? %裝載模擬信號
ls=length(s);
t=[0:ls-1]*dalt;
subplot(511);plot(t,s);Ylabel('S');???? %顯示原始信號
[C,D]=dwt(s,'db4');???????????????????? %用小波db4對信號進行單尺度分解
subplot(523);plot(C);Ylabel('C');?????? %顯示低頻分解系數
subplot(524);plot(D);Ylabel('D');?????? %顯示高頻分解系數
SCR=upcoef('a',C,'db4',1,ls);?????????? %用低頻分解系數重構
SDR=upcoef('d',D,'db4',1,ls);?????????? %用高頻分解系數重構
subplot(513);plot(t,SCR);Ylabel('SCR'); %顯示低頻重構信號
subplot(514);plot(t,SDR);Ylabel('SDR'); %顯示高頻重構信號
SR=idwt(C,D,'db4',ls);????????????????? %對信號進行完全重構
subplot(515);plot(t,SR);Ylabel('SR');?? %顯示完全重構后的信號? 】
11.2.4多尺度分解與重構
xsf11_
【? clear;
load singal1;?????????????????????????? %裝載模擬信號
ls=length(s);
t=[0:ls-1]*dalt;
subplot(711);plot(t,s);Ylabel('S');???? %顯示原始信號
??? [C,L]=wavedec(s,3,'db4');??????????? %用小波db4對信號進行多尺度分解（三層）
C3=appcoef(C,L,'db4',3);??????????????? %提取最低頻分解系數
D3=detcoef(C,L,3);???????????????????????? %提取次低頻分解系數
D2=detcoef(C,L,2);??????????????????????? %提取次高頻分解系數
D1=detcoef(C,L,1);??????????????????????? %提取最高頻分解系數
subplot(789);plot(C3);Ylabel('C');
subplot(7,8,10);plot(D3);
subplot(746);plot(D2);
subplot(724);plot(D1);
SRC3=wrcoef('a',C,L,'db4',3);???????????? %用最低頻分解系數重構
SRD3=wrcoef('d',C,L,'db4',3);???????????? %用次低頻分解系數重構
SRD2=wrcoef('d',C,L,'db4',2);???????????? %用次高頻分解系數重構
SRD1=wrcoef('d',C,L,'db4',1);???????????? %用最高頻分解系數重構
subplot(713);plot(t,SRC3);Ylabel('SRC3');
subplot(714);plot(t,SRD3);Ylabel('SRD3');
subplot(715);plot(t,SRD2);Ylabel('SRD2');
subplot(716);plot(t,SRD1);Ylabel('SRD1');
SR=waverec(C,L,'db4');??????????????????? %對信號進行完全重構
subplot(717);plot(t,SR);Ylabel('SR'); 】
11.3 應用、思考與練習
11.3.1信號的奇異性檢測