在開始查找PLL的最佳配置之前,需要考慮的是如何才能為PLL找到配置。具體而言,我們應找到PLL針對給定參考振蕩器和所需輸出頻率所使用的所有可行配置。只有在確保獲得能夠滿足需要的全部可行配置列表之后,我們才能確定哪一種樹最好的。實際上,明確最佳PLL配置的大部分工作都涉及如何找到滿足我們需求的全部可行配置列表。有鑒于此,本文將首先集中討論所有可行的配置,然后再找出最佳的選擇方案。
整數除PLL頻率合成概述
從最基本的角度而言,任何頻率合成器都旨在根據給定的參考頻率生成所需的輸出頻率,即如下所示:
其中,κ代表的是指頻率定標常量,有時也被視作標準頻率。任何頻率合成器電路都是一種趨近于κ的機制。概括介紹生成κ的方法不在本文的討論范疇之內(不過今后可以撰文加以介紹)。我們在本文中將專門討論整數除PLL頻率合成器。PLL頻率合成器在參考振蕩器和輸出時鐘之間插入分隔塊以趨近于κ。然后使用帶有相位偵測器的反饋回路在兩個分隔器之間保持相位相干性,最終生成所需的輸出頻率。相關的方框圖如圖1所示。該圖顯示了一種通用式充電泵整數除鎖相回路。
三個分隔塊用來趨近κ值:參考分隔器(Q)、反饋分隔器(P)和輸出分隔器(N)。我們很容易就能看出,針對此類頻率合成器,k的定義為:
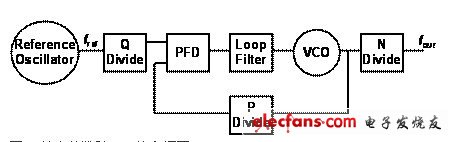
圖1. 基本整數除PLL的方框圖
結合方程式1和方程式2,我們可得出輸入和輸出頻率之間的關系:
圖1所示通用式的一般變體是將N設為1,Q設為1,或二者皆設為1的形式。這些都是根據系統設計需要而簡化的。對這三種簡化形式的分析是圖1所示一般情況的一個子集。如果Q和N都設為1,那么輸出頻率的最大分辨率限定于參考頻率,這樣我們就只能合成整數參考倍數。在此情況下,P值的確定就成了較簡單的算術問題。如果Q或N設為1,那么合成所需輸出只存在單一的配置(最小Q/P或N/P比)。這時需要進行約分才能確定比值。
使用全部三個分隔塊會給硬件增加一個通用層,可以通過對許多不同頻率合成應用編程而直接重用PLL。不過,這種通用性也導致確定P、Q和N的使用值極為困難。具體而言,這會造成單個參考和輸出頻率存在多種配置,而且所有這些配置都有著極為不同的性能特點(功耗、啟動時間、抖動、相位噪聲等)。
可編程SoC中使用的另一種配置方法是采用多個輸出分隔器,這能生成多個不同頻率的輸出(不過仍是VCO頻率的整數倍數)。圖2顯示的是這種配置的具體情況。?
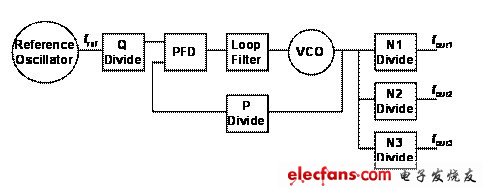
圖2. 帶多個輸出分隔器的基本整數除PLL方框圖
為可編程PLL查找所有可行的配置?
那么,就給定的一系列系統要求而言,我們如何選擇P、Q和N的分隔值呢?首先,我們討論一下稍微改變一下方程式3的一種變體:把所有已知的值放在右邊,所有未知的值放在左邊:
對任意參考和輸出頻率來說,求解方程式4的難點是存在三級自由度(僅由P、Q和N可能的分隔值范圍決定)。求解方程式4最常見的辦法就是采取搜索算法。這種算法會搜索解決方案空間,查找獲得所需值的P、Q和N值集合。這種算法本質上屬于搜索所有可行P、Q和N值的三嵌套回路。大多數PLL配置軟件都在使用這種搜索算法。圖3顯示的是這種算法實施方法的概念偽碼。請注意,為了僅可靠地生成有用配置,需要為該代碼添加許多實際的系統約束。
Figure 3.? Pseudo code for calculating divide values
圖3. 計算分隔值的偽碼
for n=Nmin; n < Nmax; n++?
??? for q=Qmin; q < Qmax; q++
??????? for p=Pmin; p < Pmax; p++
??????????? if p /(q*n)==(fout/fref)
??????????????? save [p,q,n]
????????????else
??????????????? continue
示例?
我們在示例中將從14.3181818…MHz參考(常見的視頻應用頻率)中合成50MHz輸出。假定VCO的頻率范圍為100MHz到400MHz。我們使用類似于圖3所示的搜索算法,可生成如表1所示的結果。該表列出了滿足我們需要的所有可行配置。現在,我們需要從中選出“最佳”選擇。
?
|
Table 1.? Summary of Example Results 表1. 示例結果匯總 |
||||||
|
N |
Fref [MHz] |
fvco [MHz] |
Fout [MHz] |
fpfd [MHz] |
Q |
P |
|
2 |
14.318… |
100 |
50 |
0.227 |
63 |
440 |
|
3 |
14.318… |
150 |
50 |
0.682 |
21 |
220 |
|
4 |
14.318… |
200 |
50 |
0.227 |
63 |
880 |
|
5 |
14.318… |
250 |
50 |
0.227 |
63 |
1100 |
|
6 |
14.318… |
300 |
50 |
0.682 |
21 |
440 |
|
7 |
14.318… |
350 |
50 |
1.591 |
9 |
220 |
|
8 |
14.318… |
400 |
50 |
0.227 |
63 |
1760 |
選擇最佳配置?
我們現在已經找到了滿足頻率需求的所有配置,接下來將集中精力選擇“最佳”配置。“最佳”配置完全取決于不同的應用。就遠程監控站而言,我們需要快速喚醒部件,但對準確度的要求不是太高。對通信協議而言,我們不太在意啟動時間或功耗,只需要極低的抖動時鐘源。當然我們也可能同時面臨著兩種應用需求。在數據采集階段,我們可能只需要快速喚醒功能,而在數據傳輸階段,則需要較高的準確度。利用可編程PLL和可編程SoC,我們可以同時實現上述兩種要求,但前提條件是知道采用哪種配置。?
我們將在此討論針對不同應用而優化的幾種常見PLL參數。表2總結了這些參數、相應的關鍵回路參數、以及優化方法。請注意,不是所有的可編程PLL都能為您提供以上所列出的全部參數。
功耗
功耗取決于VCO頻率、充電泵電流和分隔塊的設置。大多數VCO架構都要求較大的末端電流來提高頻率。因此,隨著頻率的升高,功耗也會增加。每個PFD期間都會有一次充電泵電流放電。如果需要更高的充電泵電流(滿足回路穩定或快速啟動/穩定時間的要求),則每個PFD期間功耗的更高。時鐘分隔器在每個時鐘脈沖邊沿都會消耗功耗。時鐘分隔值越高,則需要更多的分隔單元進行轉換,這也增加了功耗。
啟動時間 / 穩定時間
充電泵PLL的啟動和穩定時間取決于回路自然頻率。該參數可視為PLL的頻率轉換速率,它對PLL改變輸出頻率的速度加以量化。它同VCO增益和充電泵電流成正比,而與反饋分隔值和回路濾波器電容成反比。為了最小化啟動時間,我們應最大化VCO增益和充電泵電流,并最小化反饋分隔設置和回路濾波器電容。
抖動
與啟動時間/穩定時間一樣,PFD頻率和VCO增益也會對抖動產生很大影響。PFD頻率越高,就意味著PLL回路濾波器電壓刷新的頻率越高。這會避免回路濾波器電壓漂移。使用回路濾波器電容,每個PFD期間的電壓漂移量可以最小化。由于VCO增益決定著回路濾波器上單位電壓漂移的輸出頻率漂移量,因此降低VCO增益可降低PLL對回路濾波器電壓漂移的敏感度。
相位噪聲
優化相位噪聲與具體的應用密切相關,但我們這里還是要指出以下問題。一般而言,我們可將PLL設為較低的閉環帶寬,從而抑制參考振蕩器產生的相噪聲,設置PLL為較高的閉環帶寬則能抑制VCO產生的相噪聲。
我們還可通過控制輸出分隔器(N)這一參數來降低相位噪聲。相位噪聲分隔與輸出分隔的設置相關。如果輸出分隔器為低噪聲分隔器,那么運行高頻VCO并分隔輸出頻率將改進相位噪聲性能。
?
?
?
|
表2. 可編程PLL的優化參數 |
||
|
參數 |
關鍵回路參數 |
優化 |
|
功耗 |
VCO頻率(fvco) |
最小化fvco |
|
啟動時間 / 穩定時間 |
PFD頻率(fpfd) |
最大化fpfd |
|
抖動 (循環間) |
PFD頻率(fpfd) |
最大化fpfd |
|
相位噪聲 |
閉環帶寬 |
最大化fvco |
最后,我們將上述通用性優化措施應用于上例中找出的一系列PLL配置。
功耗
如果設計的主要目的是確保低功耗,那么我們應最小化VCO頻率和分隔值,因此選擇N=3、Q=21、P=220將是最佳選擇。這時,VCO頻率較低,P和Q的值較低,而且PFD頻率也比較合理。
啟動 / 穩定時間
如果我們主要關切啟動/穩定時間,那么從表1中我們可以明顯看出,N=7、Q=9、P=220是最佳選擇。這時,fPFD超過其他配置的兩倍以上,從而提升回路濾波器電壓的刷新率。
抖動
如果我們主要關切低抖動,那么N=7、Q=9、P=220仍是最佳選擇。這時,fPFD比其他配置高出兩倍多,從而讓回路濾波器電壓的刷新率得以提升,并實現所有可能配置中的最低抖動。差別在于我們應當為低抖動選擇較大的回路濾波器電容和較低的Kvco。
相位噪聲
優化相位噪聲在很大程度上取決于不同的應用以及具體的參考振蕩器和VCO噪聲性能。我們根據配置列表可做的一個設計選擇就是選用經過分隔的較高VCO頻率。N=7、Q=9、P=220可能是最佳選擇,因為其PFD頻率大大高于N=8、Q=63、P=1760時的PFD頻率。如果回路的抖動較高,將大幅提高相位噪聲水平,進而會抵消輸出分隔器所帶來的任何收益。
 電子發燒友App
電子發燒友App
























評論