MPU-6000（6050）為全球首例整合性6軸運動處理組件，相較于多組件方案，免除了組合陀螺儀與加速器時間軸之差的問題，減少了大量的封裝空間。運動感測游戲 現實增強 電子穩像 （EIS： Electronic Image Stabilization） 光學穩像（OIS： Optical Image Stabilization） 行人導航器 “零觸控”手勢用戶接口 姿勢快捷方式 認證

　　MPU6050互補濾波法融合四元數姿態原理及代碼

　　小四軸的飛行，姿態檢測主要用到的傳感器是MPU6050。從MPU6050讀出來的加速度和角速度數據最后要轉成姿態，可以轉換成歐拉角（偏航角、俯仰角和滾轉角）或四元數表示，為了減少計算量（歐拉角涉及正弦運算，運算量相對較大），方便在STM32主控上實現，可以轉換成四元數表示。

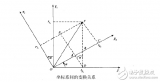
　　那么問題來了，四元數姿態融合算法哪家強？這里介紹圓點博士小四軸飛控開源代碼關于四元數姿態融合的算法以及代碼實現，不能說最強（國外有很多優秀的飛控算法），只是實現效果可以滿足小四軸的成功飛行，個人水平渣渣，請大牛批評指正。博士的代碼中主要用到的是互補濾波法。下圖為該方法的原理圖（來自論文：禤永俊，《《四軸飛行器遙感平臺的實現方案》》）。

　　先介紹一下互補濾波的基本概念，這是阿莫論壇上一個會員的總結：對mpu6050來說，加速度計對四軸或小車的加速度比較敏感，取瞬時值計算傾角誤差比較大；而陀螺儀積分得到的角度不受小車加速度的影響，但是隨著時間的增加積分漂移和溫度漂移帶來的誤差比較大。所以這兩個傳感器正好可以彌補相互的缺點。

　　不過要怎么彌補呢？經過上面的介紹是否感覺到可以用濾波器做文章呢？這里講的互補濾波就是在短時間內采用陀螺儀得到的角度做為最優，定時對加速度采樣來的角度進行取平均值來校正陀螺儀的得到的角度。就是，短時間內用陀螺儀比較準確，以它為主；長時間用加速度計比較準確，這時候加大它的比重，這就是互補了，不過濾波在哪里？加速度計要濾掉高頻信號，陀螺儀要濾掉低頻信號，互補濾波器就是根據傳感器特性不同。

　　通過不同的濾波器（高通或低通，互補的），然后再相加得到整個頻帶的信號，例如，加速度計測傾角，其動態響應較慢，在高頻時信號不可用，所以可通過低通抑制高頻；陀螺響應快，積分后可測傾角，不過由于零漂等，在低頻段信號不好。通過高通濾波可抑制低頻噪聲。將兩者結合，就將陀螺和加表的優點融合起來，得到在高頻和低頻都較好的信號，互補濾波需要選擇切換的頻率點，即高通和低通的頻率。

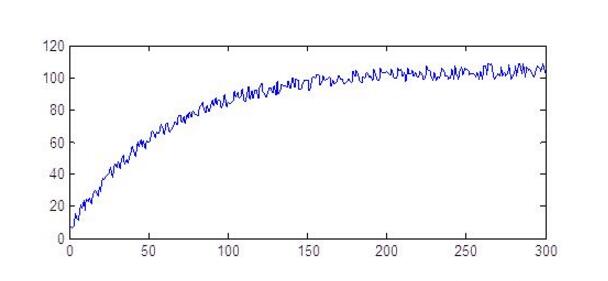
　　我個人覺得互補濾波在博士代碼里的基本思想是以角速度積分得到角度為主進行姿態解算，但是由于周圍環境或自身器件的原因，角速度計積分出來的角度可能會產生誤差的累積，長時間可能引起嚴重的角度偏移，而加速度計雖然精度不高但沒有積累誤差，可以用來對角度進行糾正。通過上位機采集互補濾波法融合的四元數姿態數據并顯示如下圖，實驗證明，這種算法很好的消除了角度偏移。

　　下面來討論加速度計測出來的加速度向量如何糾正角度：

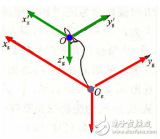
　　（1）首先是要用上一次融合的四元數估測出機坐標系下的重力加速度向量，地理坐標系下的重力加速度向量是r（E）=［0 0 1］，這里要將地理坐標系下的重力加速度轉換成機坐標系下的重力加速度，如下（具體參考：秦永元，《慣性導航-第二版》，P251）

　　r（E）=C（E-》A）r（A） //E（earth）表示r（E）是地理坐標系下的重力加速度向量，C（E-》A）表示從地理坐標系（E:earth）轉換成機（A:airplane）坐標系的轉換四元數矩陣

　　r（A）=R（-1）（C（E-》A））r（E） //R（-1）（C（E-》A））表示對矩陣C（E-》A）取逆

　　r（A）為估測出的機坐標系下的重力加速度向量，因為這是從上一次的姿態四元數中導出的向量，而姿態四元數主要是角速度計讀取的值的換算，所以這里只能說估測。

　　（2）然后我們要得到加速度計的重力加速度值，因為加速度計是固聯在機體上的，所以讀出來的向量是機坐標系下的加速度向量，又因為小四軸運動速度較慢，除開重力以外的加速度值一般較小，在誤差允許范圍內我們可以假定加速度計測出來的就是重力加速度向量。

　　（3）將機坐標系下的估測的重力加速度向量和加速度計測出的重力加速度向量分別規范化為a，b，然后叉積，叉積的結果為c=|a||b|sin（A）r（D），sin（A）角度偏移的正弦，r（D）為方向，小角情況下認為sin（A）=A，A為偏移的角度，而且|a|=|b|=1，故叉積后角度偏移算出來了。

　　（4）將角度偏移乘以一定的系數疊加在角速度積分結果上，為什么要乘以一定的系數？這是因為這里算出的角度偏移是以加速度計為基準的，而加速度計的誤差較大，直接疊加可能會引起比較大的震蕩，所以要乘以一定的系數FACTOR，但FACTOR不能太小，否則糾偏效果不好，具體取值可以試湊，然后在上位機觀測結果。

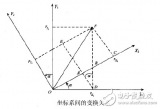
　　角度增量出來后接下來就好辦了，主要是將各種計算結果往四元數微分方程一代，結果就出來了，簡單推導如下（具體見秦永元，《慣性導航-第二版》，p254）

　　d（Q）/d（t）=1/2 × Q叉乘w（A） Q為上一次的姿態四元數，w（A）表示MPU6050讀出的機體坐標系下的角速度

　　delta（Q）=1/2 × Q叉乘（w（A） ×delta（t）+c） delta（t）為積分時間

　　Q（new）=Q+delta（Q） 新的四元數姿態求出

　　以下是代碼實現，attitude是上一次姿態融合的四元數（內存地址），gyr［3］是MPU6050讀出來的角速度，acc［3］是MPU6050讀出來的加速度，interval為積分時間。

　　void mix_gyrAcc_crossMethod（quaternion * attitude，const float gyr［3］，const float acc［3］，float interval）

　　{

　　const static float FACTOR = 0.001;//取接近0的數

　　//

　　float w_q = attitude-》w;

　　float x_q = attitude-》x;

　　float y_q = attitude-》y;

　　float z_q = attitude-》z;

　　float x_q_2 = x_q * 2;

　　float y_q_2 = y_q * 2;

　　float z_q_2 = z_q * 2;

　　//

　　// 加速度計的讀數，單位化。

　　float a_rsqrt = math_rsqrt（acc［0］*acc［0］+acc［1］*acc［1］+acc［2］*acc［2］）;

　　float x_aa = acc［0］ * a_rsqrt;

　　float y_aa = acc［1］ * a_rsqrt;

　　float z_aa = acc［2］ * a_rsqrt; //加速度計測量出的加速度向量（載體坐標系下）

　　//

　　// 載體坐標下的重力加速度向量，單位化。

　　float x_ac = x_q*z_q_2 - w_q*y_q_2;

　　float y_ac = y_q*z_q_2 + w_q*x_q_2; //通過四元數旋轉矩陣與地理坐標系下的重力加速度向量［0 0 0 1］叉乘得到載體坐標系下的重力加速度向量

　　float z_ac = 1 - x_q*x_q_2 - y_q*y_q_2;//（主要）角速度計測出的四元數表示的載體坐標系下的重力加速度向量（這里已轉換成載體坐標系下）

　　//

　　// 測量值與常量的叉積。

　　float x_ca = y_aa * z_ac - z_aa * y_ac;

　　float y_ca = z_aa * x_ac - x_aa * z_ac;

　　float z_ca = x_aa * y_ac - y_aa * x_ac;//角速度計測出的角度誤差，疊加的FACTOR大小可以實驗試湊

　　//

　　// 構造增量旋轉。

　　float delta_x = gyr［0］ * interval / 2 + x_ca * FACTOR;

　　float delta_y = gyr［1］ * interval / 2 + y_ca * FACTOR;

　　float delta_z = gyr［2］ * interval / 2 + z_ca * FACTOR;

　　//

　　// 融合，四元數乘法。

　　attitude-》w = w_q - x_q*delta_x - y_q*delta_y - z_q*delta_z;

　　attitude-》x = w_q*delta_x + x_q + y_q*delta_z - z_q*delta_y;

　　attitude-》y = w_q*delta_y - x_q*delta_z + y_q + z_q*delta_x;

　　attitude-》z = w_q*delta_z + x_q*delta_y - y_q*delta_x + z_q;

　　quaternion_normalize（attitude）;//歸一化

　　}