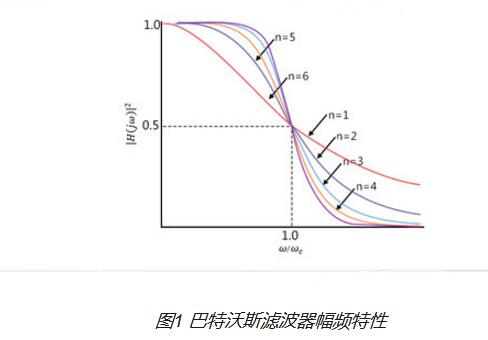
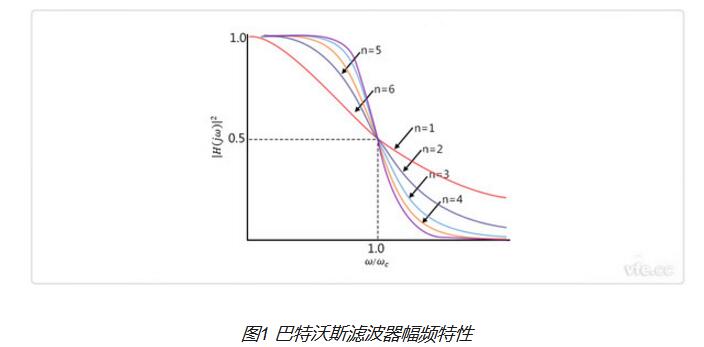
巴特沃斯濾波器的特點(diǎn)是通頻帶內(nèi)的頻率響應(yīng)曲線最大限度平坦，沒有起伏，而在阻頻帶則逐漸下降為零。 在振幅的對數(shù)對角頻率的波特圖上，從某一邊界角頻率開始，振幅隨著角頻率的增加而逐步減少，趨向負(fù)無窮大。

一階巴特沃斯濾波器的衰減率為每倍頻6分貝，每十倍頻20分貝。二階巴特沃斯濾波器的衰減率為每倍頻12分貝、三階巴特沃斯濾波器的衰減率為每倍頻18分貝、如此類推。巴特沃斯濾波器的振幅對角頻率單調(diào)下降，并且也是唯一的無論階數(shù)，振幅對角頻率曲線都保持同樣的形狀的濾波器。只不過濾波器階數(shù)越高，在阻頻帶振幅衰減速度越快。其他濾波器高階的振幅對角頻率圖和低級數(shù)的振幅對角頻率有不同的形狀。

設(shè)計步驟

如設(shè)計一個數(shù)字低通濾波器，其技術(shù)指標(biāo)為：

通帶臨界頻率fp ，通帶內(nèi)衰減小于rp；

阻帶臨界頻率fs，阻帶內(nèi)衰減大于αs；采樣頻率為FS

1、將指標(biāo)變?yōu)榻穷l率 wp=fp*2*pi;ws= fs*2*pi;

2、將數(shù)字濾波器的頻率指標(biāo){Wk}由wk=（2/T）tan（Wk/2）轉(zhuǎn)換為模擬濾波器的頻率指標(biāo){wk}，由于是用雙線性不變法設(shè)計，故先采取預(yù)畸變。

3、將高通指標(biāo)轉(zhuǎn)換為低通指標(biāo)，進(jìn)而設(shè)計高通的s域模型

4、歸一化處理

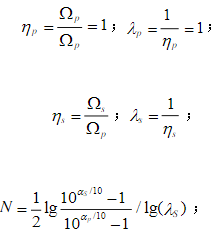
由以上三式計算出N，查表可得模擬低通濾波器的階數(shù)，從而由下式確定模擬高通濾波器的參數(shù)。

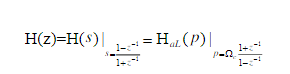
仿真程序的設(shè)計與調(diào)試

數(shù)字域指標(biāo)變換成模擬域指標(biāo)

其程序為：

fp = 400 fs= 300;

Rp = 1; Rs = 20;

wp =fp*2*pi;

ws =fs*2*pi;

FS=1000;T=1/FS；

程序執(zhí)行結(jié)果為：wp=2.5133e+003 ws=1.8850e+003 與實(shí)際計算結(jié)果相符。

數(shù)字域頻率進(jìn)行預(yù)畸變

其程序為：

wp2=2*tan（Wp/2）/T;

ws2=2*tan（Ws/2）/T;

經(jīng)過預(yù)畸變，可以發(fā)現(xiàn)頻率變?yōu)椋?wp2= 6.1554e+003

ws2= 2.7528e+003

模擬濾波器的設(shè)計

其程序為

%設(shè)計模擬濾波器

［N，Wn］ = buttord（wp2，ws2，Rp，Rs，‘s’）

武漢理工大學(xué)《數(shù)字信號處理》報告

9

［z，p，k］=buttap（N）; %創(chuàng)建Buttord低通濾波器原型

［Bap，Aap］=zp2tf（z，p，k）; %由零極點(diǎn)轉(zhuǎn)換為傳遞函數(shù)的形式

figure（1） freqs（Bap，Aap）; %模擬低通濾波器的頻率響應(yīng)

title（‘模擬濾波器（低通原型）的頻率響應(yīng)’）

［Bbs，Abs］=lp2hp（Bap，Aap，Wn）; %模擬低通變高通

figure（2）

freqs（Bbs，Abs）;

title（‘模擬濾波器的頻率響應(yīng)’）

程序執(zhí)行后可以發(fā)現(xiàn)其頻率響應(yīng)為： N=4，其波形如下圖

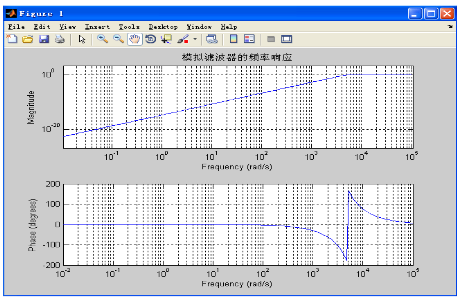
模擬濾波器的頻率響應(yīng)

由上圖分析可得：其符合高通的一般特征，與預(yù)期的效果一樣。 而在此條件下，Butterworth濾波器低通原型的波形如下圖。

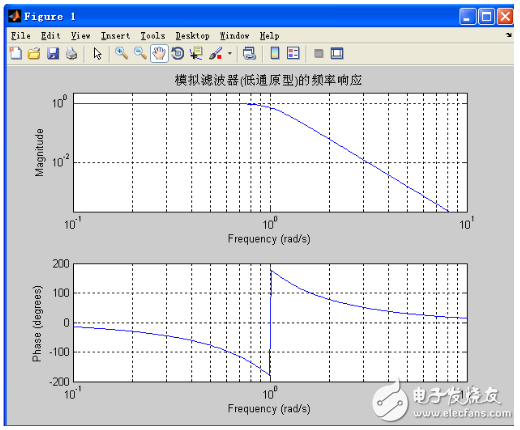
模擬濾波器（低通原型）的頻率響應(yīng)

在設(shè)計的過程中，涉及一個頻率變換的問題，即將模擬低通原型變?yōu)楦咄ǎ浜瘮?shù)及用法如下：

［b，a］=lp2hp（Bap，Aap，Wn）;

功能：把模擬濾波器原型轉(zhuǎn)換成截至頻率為 Wn 的高通濾波器。 其中，Bap，Aap分別為低通傳遞函數(shù)的分子向量和分母向量；

b，a分別為高通傳遞函數(shù)的分子向量和分母向量。

模擬濾波器變成數(shù)字濾波器

其程序為：

［Bbz，Abz］=bilinear（Bbs，Abs，F(xiàn)S）; %用雙線性變換法設(shè)計數(shù)字濾波器 freqz（Bbz，Abz，512，F(xiàn)S）;

程序運(yùn)行的結(jié)果為：如下圖

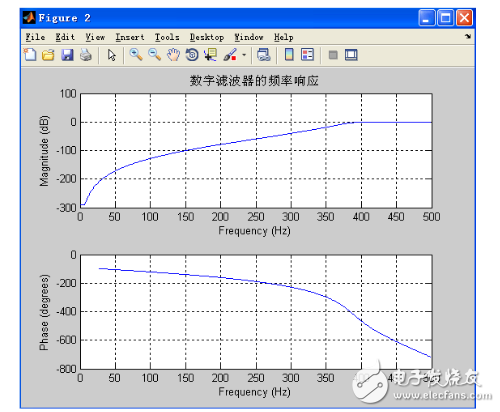
數(shù)字濾波器的頻率響應(yīng)

由于使用的是雙線性不變法設(shè)計的，其相位為非線性。此處主要是基于要獲得嚴(yán)格的頻率響應(yīng)，以及較準(zhǔn)確地控制截止頻率的位置，故畫出了詳細(xì)的幅頻響應(yīng)。（如下圖）

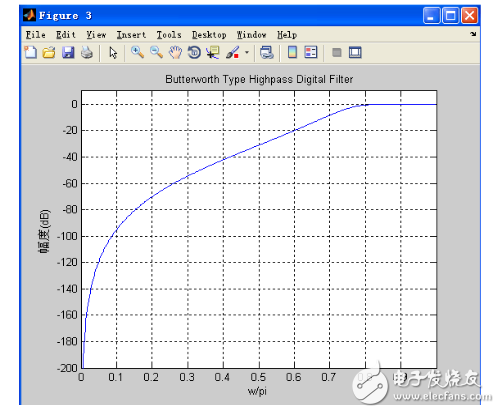
詳細(xì)的幅頻響應(yīng)

分析該圖可知其在0.6（即300Hz）處的衰減為40dB，而在0.8（即400Hz）處的衰減極小，應(yīng)小于1dB。由此可見，此設(shè)計符合要求設(shè)計的參數(shù)。

而在調(diào)試的過程中發(fā)現(xiàn)：通帶衰減越小，濾波器的性能越好 阻帶衰減越大，濾波器的性能越好 其曲線也越陡峭，選擇性越好，當(dāng)然所用的濾波器階數(shù)也越高。

當(dāng)阻帶衰減變?yōu)?0dB（之前為20dB），通帶不變時，其波形如下圖。對比上圖可知，其在阻帶臨界頻率處衰減變?yōu)榱?0dB，曲線變陡峭了。

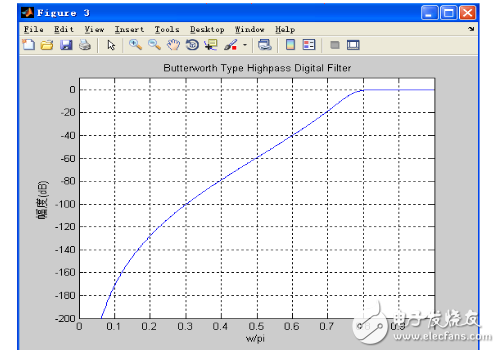
詳細(xì)的幅頻響應(yīng)（阻帶衰減為40dB）

當(dāng)通帶變?yōu)?dB時，阻帶不變時，其波形如下圖。對比圖3-3可知，其在通帶處的衰減變?yōu)榱?dB，曲線平滑了一些。

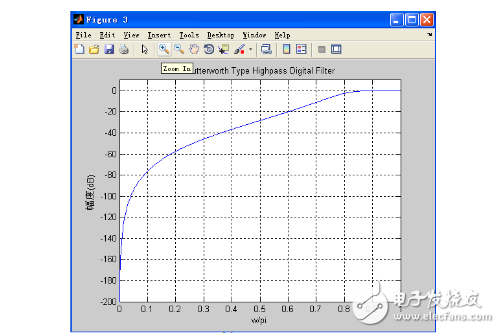
詳細(xì)的幅頻響應(yīng)（通帶衰減為5dB）

理論計算數(shù)字濾波器的仿真

wp=0.8*pi;

ws=0.6*pi;

OmegaP=2*1000*tan（wp/2）;

OmegaS=2*1000*tan（ws/2）;

lamdas=OmegaP/OmegaS;

N=0.5*log10（（10.^（20/10）-1）/（10.^（1/10）-1））/log10（lamdas）;

%筆算的結(jié)果為N=3.6947；故取N=4 %

此處為計算高通的傳遞函數(shù) Wn= 4.8890e+003 az=［0 0 0 0 1］;

bz=［1 2.613 3.414，2.613，1］; ［Bbs，Abs］=lp2hp（az，bz，Wn） %用雙線性不變法處理

［Bbz，Abz］=bilinear（Bbs，Abs，1000）; 其運(yùn)行結(jié)果為：N=3.6947；圖形如下圖

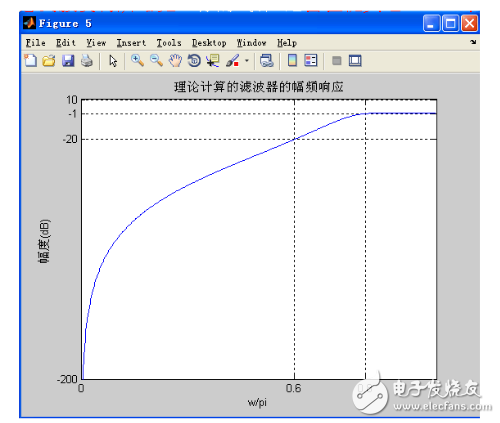
理論計算的濾波器的幅頻響應(yīng)

綜上所述，本濾波器以四階即實(shí)現(xiàn)了預(yù)期的設(shè)計目標(biāo)：采樣頻率為1000Hz，通帶臨界頻率fp =400Hz，通帶內(nèi)衰減小于1dB（αp=1）；阻帶臨界頻率fs=300Hz，阻帶內(nèi)衰減大于20dB（αs=25），其在通帶內(nèi)的性能更好。