模數轉換器（ADC）有多種規格描述（specification）。根據應用需求，其中一些規范可能比其他規范更重要。

比如：在直流規格中，如失調誤差、增益誤差、積分非線性（INL）和差分非線性（DNL），在使用ADC對慢速移動信號（如應變片和溫度傳感器的信號）進行數字化處理的儀器儀表應用中尤為重要。

本文深入探討失調和增益誤差規格。

模數轉換器傳遞函數

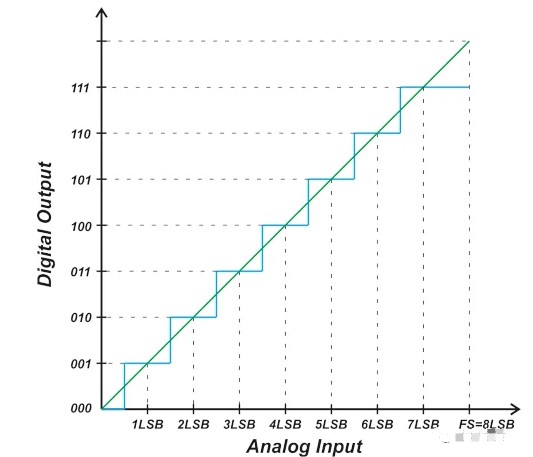
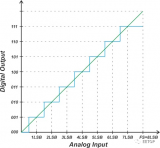
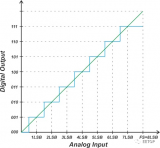
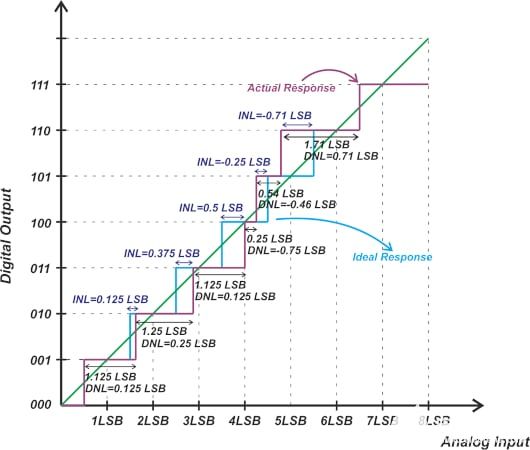
3-bit單極性ADC的理想傳遞函數如圖1所示。

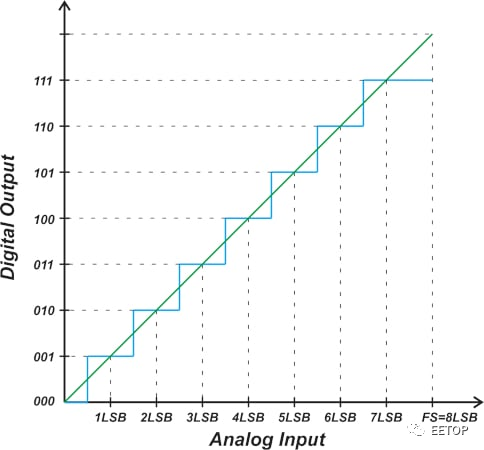
圖1. 3-bit單極性ADC的數字輸出與模擬輸入（傳遞函數）

理想情況下，ADC具有均勻的階梯輸入-輸出特性。請注意，輸出編碼不對應于單個模擬輸入值。相反，每個輸出碼代表一個小的輸入電壓范圍，寬度等于一個LSB（最低有效位）。

如上圖所示，第一次輸出碼轉換發生在0.5 LSB，此后每個連續的轉換發生在上一個轉換的1 LSB處。最后一次躍遷發生在低于滿量程（FS）值1.5 LSB處。

由于使用有限數量的數字碼來表示連續范圍的模擬值，因此ADC表現出階梯響應，這本質上是非線性的。

在評估某些非理想效應（如失調誤差、增益誤差和非線性）時，通過穿過階躍中點的直線對ADC傳遞函數進行建模非常有用。這條線可以用以下等式表示：

[Y_{Linear}=frac{V_{in}}{FS} imes2^{N}]

其中 Vin是輸入電壓，N表示位數。如果我們不斷提高ADC分辨率（或輸出代碼的位數），階梯響應將越來越接近線性模型。

因此，直線可以被視為具有無限數量輸出代碼的理想ADC的傳遞函數。然而，在實踐中，我們知道ADC分辨率是有限的，直線只是實際響應的線性模型。

ADC失調誤差和傳遞函數

由于內部元件不匹配等非理想效應，ADC的實際傳遞函數會偏離理想的階梯響應。偏移誤差沿水平軸移動傳遞函數，從而導致代碼轉換點偏移。圖2中的紫色曲線顯示了失調為+1 LSB的ADC的響應。

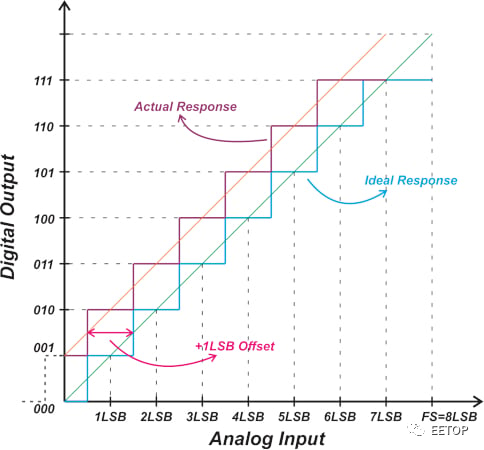
圖2. 顯示 +1 LSB 偏移、實際響應和理想響應的圖表。

對于單極性三位理想ADC，第一次轉換應發生在0.5 LSB，將輸出從000變為001。但是，在上述響應下，ADC輸出在0.5 LSB時從001轉換到010。

理想情況下，001到010的躍遷應該發生在1.5 LSB處。因此，與理想特性相比，非理想響應向左移動1 LSB。這稱為+1 LSB失調誤差。

考慮非理想響應的線性模型（圖中的橙色曲線），我們還可以觀察到，對于0V輸入，系統輸出001，對應于+1 LSB失調。 圖3顯示了失調誤差為-1.5 LSB的ADC的響應。 ?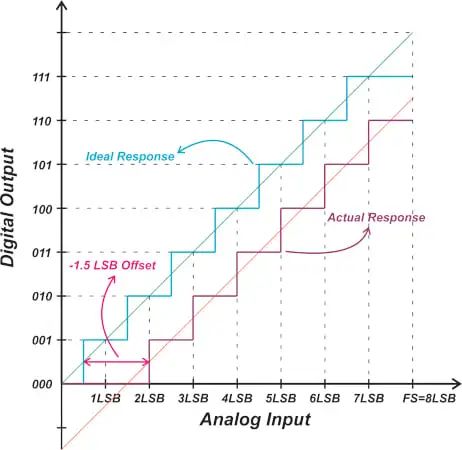

圖3. 具有-1.5 LSB失調誤差的ADC響應。

由于失調誤差將整個傳遞函數偏移相同的值，因此可以通過從ADC輸出中減去失調值來輕松校準。為了確定失調誤差，通常測量第一次代碼轉換，并將其與理想響應的相應轉換進行比較。

使用第一個代碼轉換（而不是下一個代碼轉換）可以產生更準確的測量，因為根據定義，失調誤差是指零伏輸入時與理想響應的偏差。

查找ADC失調誤差示例

考慮滿量程值為FS = 5 V的10位ADC。如果從全零輸出代碼過渡到 00...01發生在8 mV的輸入電壓下，ADC的失調誤差是多少？

對于FS = 5 V的10位ADC，LSB值為4.88 mV，計算如下：

[LSB=frac{FS}{2^{N}}=frac{5}{2^{10}}=4.88,mV]

理想情況下，第一次躍遷應在0.5 LSB = 2.44 mV時發生，而測得的響應在8 mV時發生這種躍遷。因此，ADC的失調值為-5.56 mV。失調誤差也可以表示為LSB的倍數，如下所示：

[Offset,Error,(in,LSB)=frac{Offset,Error,(in, Volts)}{LSB,Value,(in, Volts)} = frac{-5.56,mV}{4.88,mV}=-1.14,LSB]

模數轉換器增益誤差

消除失調誤差后，實際響應的第一次轉換與理想特性的轉換一致。但是，這并不能保證兩條特征曲線的其他轉換也將在相同的輸入值下發生。增益誤差指定上次躍遷與理想值的偏差。圖4說明了增益誤差概念。

?

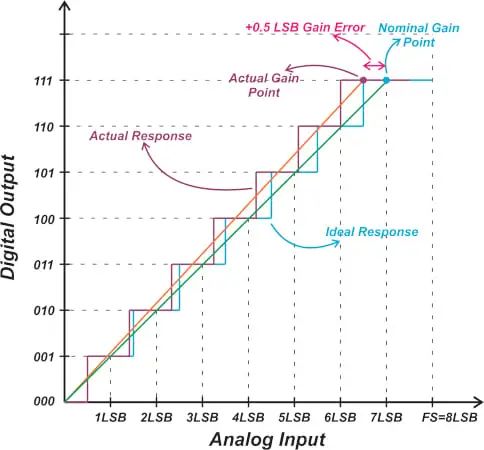
圖4. 顯示增益誤差概念的圖表。

讓我們將上一次轉換上方的一半LSB定義為“增益點”。消除失調誤差后，理想增益點與實際增益點之差決定了增益誤差。

在上例中，非理想特性的增益誤差為+0.5 LSB。上圖中的橙色曲線是非理想響應的線性模型。

如您所見，測量增益點和理想增益點之間的差異實際上會改變系統線性模型的斜率。圖5顯示了具有-1 LSB增益誤差的ADC的響應。

?

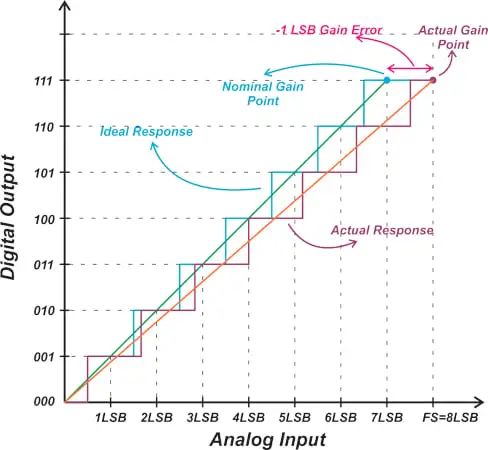
圖5. 具有-1 LSB增益誤差的ADC的響應。

請注意，一些技術文檔將增益誤差定義為理想ADC的實際增益點與直線模型之間的垂直差。在本例中，繼續圖 5 中描述的示例，我們得到圖 6 中的圖表。

?

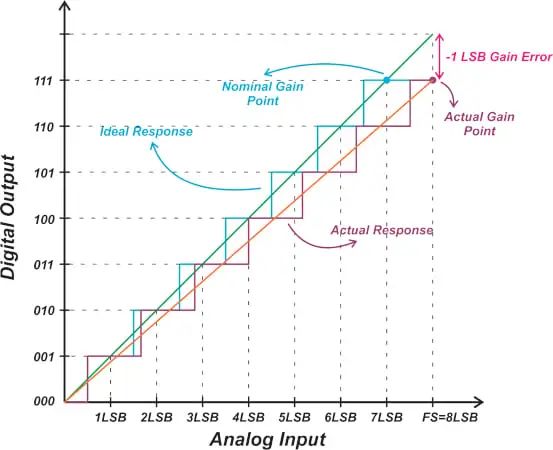
圖6. 增益誤差為ADC實際增益點與直線模型之間的垂直差值。

垂直和水平差異產生相同的結果，因為理想線性模型的斜率為 1。

查找ADC增益誤差示例

假設滿量程值為FS = 5 V的10位ADC在4.995 V時從3FE的十六進制值最后一次轉換到3FF。假設失調誤差為零，計算ADC增益誤差。

ADC的LSB為4.88 mV，如上例所示。理想情況下，最后一次轉換應發生在FS -1.5 LSB = 4992.68 mV時。發生躍遷時的測量值為4995 mV。因此，ADC的增益誤差為-2.32 mV或-0.48 LSB。

用滿量程誤差表示增益誤差

基于上述概念，我們可以根據滿量程誤差來定義增益誤差。如圖 7 所示。

?

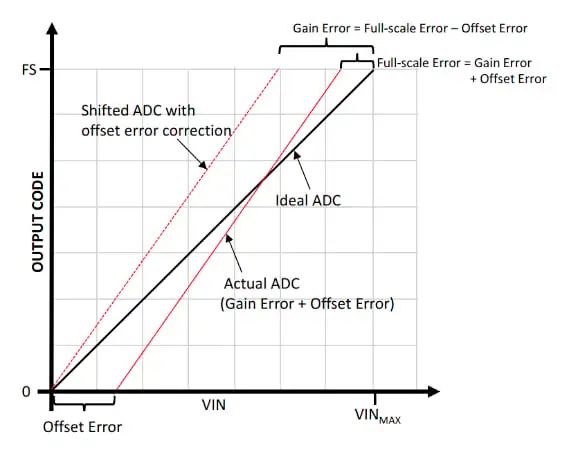
圖7.滿量程誤差。圖片由Microchip提供

在上圖中，實際響應受到失調和增益誤差的影響。因此，實際最后一次轉換與理想最后一次轉換的偏差（用滿量程誤差表示）包含失調和增益誤差。為了找到增益誤差，我們可以從滿量程誤差中減去失調誤差：

[Gain Error,=,Full scale Error,-,Offset Error]

這相當于首先補償失調誤差，然后測量與理想響應的最后一次躍遷的偏差，以得出增益誤差。請注意，在本例中，增益誤差為正，失調誤差為負，導致滿量程誤差小于增益誤差。

定義中的一些ADC規格不一致

值得一提的是，一些ADC規格在技術文獻中定義不一致。一個令人困惑的不一致是失調和增益誤差的標志。例如，雖然Microchip和Maxim Integrated與本文中使用的定義一致，但一些制造商，如STMicroelectronics（ST）有所不同。ST以相反的方式定義這些誤差項的符號。來自同一芯片制造商的文檔之間也觀察到不一致。例如，圖 8 取自此德州儀器?（TI） 文檔，該文檔使用相反的符號約定。

?

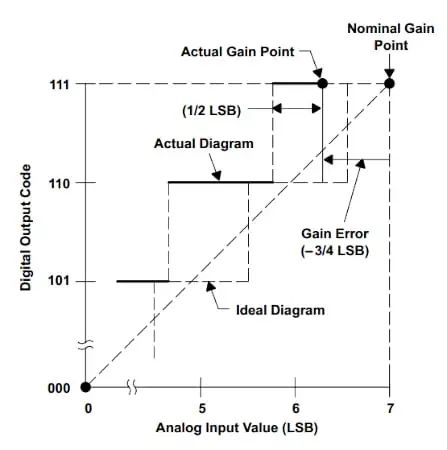
圖8.TI 的 ADC 增益誤差示例。圖片由TI提供

但是，圖 9（同樣來自 TI）使用的定義與本文中使用的定義一致。

?

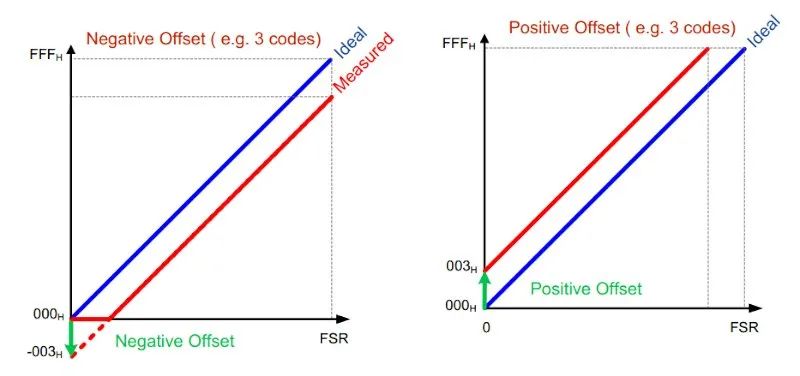
圖9.TI 失調誤差示例。圖片（改編）由 TI 提供

圖 9（以及整篇本文）中使用的符號約定似乎在各種技術文獻中得到了更廣泛的接受。盡管如此。這種不一致可能會導致混淆，但如果您掌握了本文中討論的基本概念，則可以解決此問題。例如，如果您測量ADC，并觀察到其第一次轉換發生在0.5 LSB以上（類似于圖3中描述的情況），則無論使用何種符號約定，都應在ADC讀數中添加適當的正值以補償失調誤差。

審核編輯：劉清