基于深度強(qiáng)化學(xué)習(xí)的智能船舶航跡跟蹤控制
人工智能技術(shù)與咨詢 昨天
本文來(lái)自《中國(guó)艦船研究》?,作者祝亢等
關(guān)注微信公眾號(hào):人工智能技術(shù)與咨詢。了解更多咨詢!
0.?? 引 言
目前,國(guó)內(nèi)外對(duì)運(yùn)載工具的研究正朝著智能化、無(wú)人化方向發(fā)展,智能船舶技術(shù)受到全球造船界與航運(yùn)界的廣泛關(guān)注。其以實(shí)現(xiàn)船舶航行環(huán)境的智能化、自主化發(fā)展為目標(biāo),深度融合傳統(tǒng)船舶設(shè)計(jì)與制造技術(shù)以及現(xiàn)代信息通信與人工智能技術(shù),包含智能航行、智能船用設(shè)備、智能船舶測(cè)試等多方面的研究[1]。其中,智能航行技術(shù)一直是保障船舶順利完成貨物運(yùn)輸、通信救助等任務(wù)的重要基礎(chǔ)。要使船舶在面對(duì)多種復(fù)雜水域干擾的情況下也能遵守正常的通航秩序,安全地執(zhí)行任務(wù)且保證完成效果,采取有效的控制手段精確進(jìn)行航跡跟蹤就顯得尤為重要。
針對(duì)航跡跟蹤的研究任務(wù)可以分為制導(dǎo)和控制2個(gè)方面。在制導(dǎo)方面,常由視線(line-of-sight,LOS)算法將路徑跟蹤問(wèn)題轉(zhuǎn)換為方便處理的動(dòng)態(tài)誤差控制問(wèn)題;在控制方面,基于船舶的復(fù)雜非線性系統(tǒng),常考慮使用PID等無(wú)模型控制方法,或采用模型線性化的方法來(lái)解決非線性模型在計(jì)算速率方面存在的問(wèn)題。但對(duì)于復(fù)雜的環(huán)境,傳統(tǒng)PID控制器不僅參數(shù)復(fù)雜,還不具備自適應(yīng)學(xué)習(xí)能力。而最優(yōu)控制、反饋線性化一類(lèi)的控制算法通常需要建立精確的模型才能獲得較高的控制精度。滑模控制雖然對(duì)模型精度要求不高,但其抖振問(wèn)題難以消除[2]。即使存在一些自適應(yīng)參數(shù)調(diào)節(jié)方法,如通過(guò)估計(jì)系統(tǒng)輸出實(shí)現(xiàn)PID參數(shù)自整定的自適應(yīng)PID控制方法,也會(huì)由于模型的不確定性和外界擾動(dòng),存在系統(tǒng)輸出與真實(shí)輸出的偏差[3],又或者存在參數(shù)尋優(yōu)時(shí)間過(guò)長(zhǎng)的問(wèn)題而影響控制的實(shí)時(shí)性。對(duì)于與模糊邏輯相結(jié)合的響應(yīng)速度快、實(shí)時(shí)性好的PID自適應(yīng)控制器[4],其控制精度依賴(lài)于復(fù)雜的模糊規(guī)則庫(kù),致使整體計(jì)算復(fù)雜。
考慮到船舶的復(fù)雜非線性系統(tǒng)模型,和保障航跡跟蹤控制的實(shí)時(shí)性時(shí)產(chǎn)生的大量參數(shù)整定和復(fù)雜計(jì)算等問(wèn)題,本文將采用深度強(qiáng)化學(xué)習(xí)算法來(lái)研究智能船舶的軌跡跟蹤問(wèn)題。深度強(qiáng)化學(xué)習(xí)(deep reinforcement learning,DRL)是深度學(xué)習(xí)與強(qiáng)化學(xué)習(xí)的結(jié)合,其通過(guò)強(qiáng)化學(xué)習(xí)與環(huán)境探索得到優(yōu)化的目標(biāo),而深度學(xué)習(xí)則給出運(yùn)行的機(jī)制用于表征問(wèn)題和解決問(wèn)題。深度強(qiáng)化學(xué)習(xí)算法不依賴(lài)動(dòng)力學(xué)模型和環(huán)境模型,不需要進(jìn)行大量的算法計(jì)算,還具備自學(xué)習(xí)能力。Magalh?es等[5]基于強(qiáng)化學(xué)習(xí)算法,使用Q-learning設(shè)計(jì)了一種監(jiān)督開(kāi)關(guān)器并應(yīng)用到了無(wú)人水面艇,它能智能地切換控制器從而使無(wú)人艇的行駛狀態(tài)符合多種環(huán)境與機(jī)動(dòng)要求。2015年,Mnih等[6]為解決復(fù)雜強(qiáng)化學(xué)習(xí)的穩(wěn)定性問(wèn)題,將強(qiáng)化學(xué)習(xí)與深度神經(jīng)網(wǎng)絡(luò)相結(jié)合,提出了深度Q學(xué)習(xí)(deep Q network,DQN)算法,該算法的提出代表了深度強(qiáng)化學(xué)習(xí)時(shí)代的到來(lái)。之后,在欠驅(qū)動(dòng)無(wú)人駕駛船舶的航行避碰中也進(jìn)行了相關(guān)應(yīng)用[7]。
面對(duì)存在的大量參數(shù)整定、復(fù)雜算法計(jì)算等問(wèn)題,為實(shí)現(xiàn)船舶航跡跟蹤的精準(zhǔn)控制,本文擬設(shè)計(jì)一種基于深度確定性策略梯度算法(deep deterministic policy gradient,DDPG)的深度強(qiáng)化學(xué)習(xí)航跡跟蹤控制器,在LOS算法制導(dǎo)的基礎(chǔ)上,對(duì)船舶航向進(jìn)行控制以達(dá)到航跡跟蹤效果。然后,根據(jù)實(shí)際船舶的操縱特性以及控制要求,將船舶路徑跟蹤問(wèn)題建模成馬爾可夫決策過(guò)程,設(shè)計(jì)相應(yīng)的狀態(tài)空間、動(dòng)作空間與獎(jiǎng)勵(lì)函數(shù),并采用離線學(xué)習(xí)方法對(duì)控制器進(jìn)行學(xué)習(xí)訓(xùn)練。最后,通過(guò)仿真實(shí)驗(yàn)驗(yàn)證深度強(qiáng)化學(xué)習(xí)航跡控制器算法的有效性,并與BP-PID控制器算法的控制效果進(jìn)行對(duì)比分析。
1.?? 智能船舶航跡跟蹤控制系統(tǒng)總體設(shè)計(jì)
1.1?? LOS算法制導(dǎo)
航跡跟蹤控制系統(tǒng)包括制導(dǎo)和控制2個(gè)部分,其中制導(dǎo)部分一般是根據(jù)航跡信息和船舶當(dāng)前狀態(tài)確定所需的設(shè)定航向角值來(lái)進(jìn)行工作。本文使用的LOS算法已被廣泛運(yùn)用于路徑控制。LOS算法可以在模型參數(shù)不確定的情況下,以及在復(fù)雜的操縱環(huán)境中與控制器結(jié)合,從而實(shí)現(xiàn)對(duì)模型的跟蹤控制。視線法的導(dǎo)航原理是基于可變的半徑與路徑點(diǎn)附近生成的最小圓來(lái)產(chǎn)生期望航向,即LOS角。經(jīng)過(guò)適當(dāng)?shù)目刂疲巩?dāng)前船舶的航向與LOS角一致,即能達(dá)到航跡跟蹤的效果[8]。
LOS算法示意圖如圖1所示。假設(shè)當(dāng)前跟蹤路徑點(diǎn)為Pk+1(xk+1,yk+1)Pk+1(xk+1,yk+1),上一路徑點(diǎn)為Pk(xk,yk)Pk(xk,yk),以船舶所在位置Ps(xs,ys)Ps(xs,ys)為圓心,選擇半徑RLosRLos與路徑PkPk+1PkPk+1相交,選取與Pk+1Pk+1相近的點(diǎn)PLos(xLos,yLos)PLos(xLos,yLos)作為L(zhǎng)OS點(diǎn),當(dāng)前船舶坐標(biāo)到LOS點(diǎn)的方向矢量與x0x0的夾角ψLosψLos則為需要跟蹤的LOS角。圖中:dd為當(dāng)前船舶至跟蹤路徑的最短距離;ψψ為當(dāng)前航向角。
其中,半徑RLosRLos的計(jì)算公式如式(1)和式(2)所示,為避免RminRmin的計(jì)算出現(xiàn)零值,在最終的計(jì)算中加入了2倍的船長(zhǎng)LppLpp來(lái)進(jìn)行處理[9]。
|
???????????????????????????a(t)=(x(t)?xk)2+(y(t)?yk)2?????????????????????√b(t)=(xk+1?x(t))2+(y(t)?yk+1)2????????????????????????√c(t)=(xk+1?xk)2+(yk+1?yk)2??????????????????????√Rmin(t)=a(t)2?(c(t)2?b(t)2+a(t)22c(t))2???????????????????????????{a(t)=(x(t)?xk)2+(y(t)?yk)2b(t)=(xk+1?x(t))2+(y(t)?yk+1)2c(t)=(xk+1?xk)2+(yk+1?yk)2Rmin(t)=a(t)2?(c(t)2?b(t)2+a(t)22c(t))2 |
(1) |
|
RLos=Rmin(t)+2LppRLos=Rmin(t)+2Lpp |
(2) |
式中,所計(jì)算的RminRmin即為當(dāng)前時(shí)刻t的航跡誤差ε,也即圖1中的dd。
圖? 1? LOS導(dǎo)航原理圖
Figure? 1.? Schematic diagram of LOS algorithm
?
船舶在沿著路徑進(jìn)行跟蹤時(shí),若進(jìn)入下一個(gè)航向點(diǎn)的一定范圍內(nèi),即以Pk+2(xk+2,yk+2)Pk+2(xk+2,yk+2)為圓心、RACRAC為半徑的接受圓內(nèi),則更新當(dāng)前航向點(diǎn)為下一航向點(diǎn),半徑RACRAC一般選取為2倍船長(zhǎng)。
1.2?? 基于強(qiáng)化學(xué)習(xí)的控制過(guò)程設(shè)計(jì)
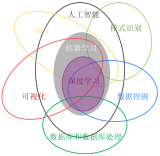
強(qiáng)化學(xué)習(xí)(reinforcement learning,RL)與深度學(xué)習(xí)同屬機(jī)器學(xué)習(xí)范疇,是機(jī)器學(xué)習(xí)的一個(gè)重要分支,主要用來(lái)解決連續(xù)決策的問(wèn)題,是馬爾可夫決策過(guò)程(Markov decision processes,MDP)問(wèn)題[10]的一類(lèi)重要解決方法。
此類(lèi)問(wèn)題均可模型化為MDP問(wèn)題,簡(jiǎn)單表示為四元組。其中,SS為所有狀態(tài)值的集合,即狀態(tài)空間;AA為動(dòng)作值集合的動(dòng)作空間;PP為狀態(tài)轉(zhuǎn)移概率矩陣,即在tt時(shí)刻狀態(tài)為St=sSt=s的情況下選擇動(dòng)作值為At=aAt=a,則t+1t+1時(shí)刻產(chǎn)生狀態(tài)為s1s1的概率Pass1=P[St+1=s1|St=s,At=a]Pss1a=P[St+1=s1|St=s,At=a];R=r(s,a)R=r(s,a)為回報(bào)獎(jiǎng)勵(lì)函數(shù),用于評(píng)價(jià)在ss狀態(tài)下選取動(dòng)作值aa的好壞。航跡跟蹤控制系統(tǒng)中的控制部分用MDP模型表示如圖2所示。,a,p,r>
圖? 2? 船舶控制的MDP模型
Figure? 2.? MDP model of ship control
?
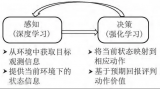
如圖2所示,船舶智能體直接與當(dāng)前控制環(huán)境進(jìn)行交互而且不需要提前獲取任何信息。在訓(xùn)練過(guò)程中,船舶采取動(dòng)作值atat與環(huán)境進(jìn)行交互更新自己的狀態(tài)st→st+1st→st+1,并獲得相應(yīng)的獎(jiǎng)勵(lì)rt+1rt+1,之后,繼續(xù)采取下一動(dòng)作與環(huán)境交互。在此過(guò)程中,會(huì)產(chǎn)生大量的數(shù)據(jù),利用這些數(shù)據(jù)學(xué)習(xí)優(yōu)化自身選擇動(dòng)作的策略policyππ。簡(jiǎn)單而言,這是一個(gè)循環(huán)迭代的過(guò)程。在強(qiáng)化學(xué)習(xí)中,訓(xùn)練的目標(biāo)是找到一個(gè)最佳的控制策略 policyπ?π?,以使累積回報(bào)值RtRt達(dá)到最大[11]。在下面的公式中,γγ為折扣系數(shù),用來(lái)衡量未來(lái)回報(bào)在當(dāng)前時(shí)期的價(jià)值比例,設(shè)定γ∈[0,1]γ∈[0,1]。
|
Rt=rt+γrt+1+γ2rt+2+?=∑k=1∞γkrt+k+1Rt=rt+γrt+1+γ2rt+2+?=∑k=1∞γkrt+k+1 |
(3) |
Policy?ππ可以使用2種值函數(shù)進(jìn)行評(píng)估:狀態(tài)值函數(shù)Vπ(st)Vπ(st)和動(dòng)作值函數(shù)Qπ(st,at)Qπ(st,at)。其中Vπ(st)Vπ(st)為在遵循當(dāng)前策略的狀態(tài)下對(duì)累積回報(bào)值的期望,EE為期望值;類(lèi)似地,Qπ(st,at)Qπ(st,at)表示基于特定狀態(tài)和動(dòng)作情況(st,at)(st,at)下對(duì)累積回報(bào)值的期望。
|
Vπ(st)=Eπ[Rt|st]=Eπ[∑k=1∞γkrt+k+1|st]Vπ(st)=Eπ[Rt|st]=Eπ[∑k=1∞γkrt+k+1|st] |
(4) |
|
Qπ(st,at)=Eπ[Rt|st,at]=Eπ[∑k=1∞γkrt+k+1|st,at]Qπ(st,at)=Eπ[Rt|st,at]=Eπ[∑k=1∞γkrt+k+1|st,at] |
(5) |
根據(jù)值函數(shù)和上述最佳控制策略policy?π?π?的定義,最佳policy?π?π?總是滿足以下條件:
|
π?=argmaxVπ(st)=argmaxQπ(st,at)π?=argmaxVπ(st)=argmaxQπ(st,at) |
(6) |
1.3?? 航跡跟蹤問(wèn)題馬爾可夫建模
從以上描述可以看出,在基于強(qiáng)化學(xué)習(xí)的控制設(shè)計(jì)中,馬爾可夫建模過(guò)程的組件設(shè)計(jì)是最為關(guān)鍵的過(guò)程,狀態(tài)空間、動(dòng)作空間和獎(jiǎng)勵(lì)的正確性對(duì)算法性能和收斂速度的影響很大。所以針對(duì)智能船舶的軌跡跟蹤問(wèn)題,對(duì)其進(jìn)行馬爾可夫建模設(shè)計(jì)。
1) 狀態(tài)空間設(shè)計(jì)。
根據(jù)制導(dǎo)采用的LOS算法,要求當(dāng)前航向角根據(jù)LOS角進(jìn)行調(diào)節(jié)以達(dá)到跟蹤效果。所以在選取狀態(tài)時(shí),需考慮LOS算法中的輸出參數(shù),包括目標(biāo)航向ψLOSψLOS與實(shí)際航向ψψ的差值ee、航跡誤差ε,以及與航跡點(diǎn)距離誤差εdεd。
對(duì)于船舶模型,每個(gè)時(shí)刻都可以獲得當(dāng)前船舶的縱蕩速度uu、橫蕩速度vv、艏轉(zhuǎn)向速度rr和舵角δδ。為使強(qiáng)化學(xué)習(xí)能實(shí)現(xiàn)高精度跟蹤效果,快速適應(yīng)多種環(huán)境的變換,除了選取當(dāng)前時(shí)刻的狀態(tài)值外,還加入了上一時(shí)刻的狀態(tài)值進(jìn)行比較,以及當(dāng)前航向誤差與上一時(shí)刻航向誤差的差值e(k?1)e(k?1),使當(dāng)前狀態(tài)能夠更好地表示船舶是否在往誤差變小的方向運(yùn)行。最終,當(dāng)前時(shí)刻t的狀態(tài)空間可設(shè)計(jì)為
|
st=[et,εt,εdt,ut,vt,rt,δt,e(k?1)t,et?1,εt?1,εdt?1,ut?1,vt?1,rt?1,δt?1]st=[et,εt,εtd,ut,vt,rt,δt,e(k?1)t,et?1,εt?1,εt?1d,ut?1,vt?1,rt?1,δt?1] |
(7) |
2) 動(dòng)作空間設(shè)計(jì)。
針對(duì)航跡跟蹤任務(wù)特點(diǎn),以及LOS制導(dǎo)算法的原理,本文將重點(diǎn)研究對(duì)船舶航向,即舵角的控制,不考慮對(duì)船速與槳速的控制。動(dòng)作空間只有舵令一個(gè)動(dòng)作值,即δδ,其值的選取需要根據(jù)實(shí)際船舶的控制要求進(jìn)行約束,設(shè)定為在(?35°,35°)(?35°,35°)以內(nèi),最大舵速為15.8 (°)/s。
3) 獎(jiǎng)勵(lì)函數(shù)設(shè)計(jì)。
本文期望航向角越靠近LOS角獎(jiǎng)勵(lì)值越高,與目標(biāo)航跡的誤差越小獎(jiǎng)勵(lì)值越高。因此,設(shè)計(jì)的獎(jiǎng)勵(lì)函數(shù)為普遍形式,即分段函數(shù):
|
rt={0,?|e|?0.1|e(k?1)|?0.01|ε|,if|e|?0.1radif|e|>0.1radrt={0,if|e|?0.1rad?|e|?0.1|e(k?1)|?0.01|ε|,if|e|>0.1rad |
(8) |
式中,e(k?1)e(k?1)為當(dāng)前航向誤差與上一時(shí)刻航向誤差的差值。當(dāng)差值大于0.1rad0.1rad時(shí)選擇負(fù)值獎(jiǎng)勵(lì),也可稱(chēng)之為懲罰值,是希望訓(xùn)練網(wǎng)絡(luò)能盡快改變當(dāng)前不佳的狀態(tài)。將負(fù)值的選取與另一分段的00獎(jiǎng)勵(lì)值做明顯對(duì)比,使其訓(xùn)練學(xué)習(xí)后可以更加快速地選擇獎(jiǎng)勵(lì)值高的動(dòng)作,從而達(dá)到最優(yōu)效果。
1.4?? 控制系統(tǒng)總體方案
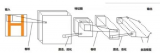
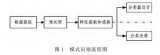
基于強(qiáng)化學(xué)習(xí)的智能船舶航跡控制系統(tǒng)總體框架如圖3所示。LOS算法根據(jù)船舶當(dāng)前位置計(jì)算得到需要的航向以及航跡誤差,在與船舶的狀態(tài)信息整合成上述所示狀態(tài)向量stst后輸入進(jìn)航跡控制器中,然后根據(jù)強(qiáng)化學(xué)習(xí)算法輸出當(dāng)前最優(yōu)動(dòng)作值atat給船舶執(zhí)行,同時(shí)通過(guò)獎(jiǎng)勵(lì)函數(shù)rtrt計(jì)算獲得相應(yīng)的獎(jiǎng)勵(lì)來(lái)進(jìn)行自身參數(shù)迭代,以使航跡控制器具備自學(xué)習(xí)能力。
圖? 3? 基于強(qiáng)化學(xué)習(xí)的智能船舶軌跡跟蹤控制框圖
Figure? 3.? Block diagram of intelligent ship tracking control based on RL
?
在將控制器投入實(shí)時(shí)控制之前,首先需要對(duì)控制器進(jìn)行離線訓(xùn)練。設(shè)定規(guī)定次數(shù)的訓(xùn)練后,將獲得的使累計(jì)回報(bào)值達(dá)到最大的網(wǎng)絡(luò)參數(shù)進(jìn)行存儲(chǔ)整合,由此得到強(qiáng)化學(xué)習(xí)控制器,并應(yīng)用于航跡跟蹤的實(shí)時(shí)控制系統(tǒng)。
要解決強(qiáng)化學(xué)習(xí)問(wèn)題,目前有許多的算法、機(jī)制和網(wǎng)絡(luò)結(jié)構(gòu)可供選擇,但這些方法都缺少可擴(kuò)展的能力,并且僅限于處理低維問(wèn)題。為此,Mnih等[6]提出了一種可在強(qiáng)化學(xué)習(xí)問(wèn)題中使用大規(guī)模神經(jīng)網(wǎng)絡(luò)的訓(xùn)練方法——DQN算法,該算法成功結(jié)合了深度學(xué)習(xí)與強(qiáng)化學(xué)習(xí),使強(qiáng)化學(xué)習(xí)也可以擴(kuò)展處理一些高維狀態(tài)、動(dòng)作空間下的決策問(wèn)題[12]。DQN算法可解決因強(qiáng)化學(xué)習(xí)過(guò)程與神經(jīng)網(wǎng)絡(luò)逼近器對(duì)值函數(shù)逼近的訓(xùn)練相互干擾,而導(dǎo)致學(xué)習(xí)結(jié)果不穩(wěn)定甚至是產(chǎn)生分歧的問(wèn)題[13],是深度強(qiáng)化學(xué)習(xí)領(lǐng)域的開(kāi)創(chuàng)者。
DQN算法顯著提高了復(fù)雜強(qiáng)化學(xué)習(xí)問(wèn)題的穩(wěn)定性和性能,但因其使用的是離散的動(dòng)作空間,故需要對(duì)輸出的動(dòng)作進(jìn)行離散化,且只能從有限的動(dòng)作值中選擇最佳動(dòng)作。對(duì)于船舶的軌跡跟蹤問(wèn)題,如果候選動(dòng)作數(shù)量太少,就很難對(duì)智能體進(jìn)行精確控制。為使算法滿足船舶的操縱特性與要求,本文選擇了一種適用于連續(xù)動(dòng)作空間的深度強(qiáng)化學(xué)習(xí)算法,即基于DDPG的算法[14]來(lái)對(duì)智能船舶航跡跟蹤控制器進(jìn)行設(shè)計(jì),該算法不僅可以在連續(xù)動(dòng)作空間上進(jìn)行操作,還可以高效精準(zhǔn)地處理大量數(shù)據(jù)。
2.?? 基于DDPG算法的控制器設(shè)計(jì)
2.1?? DDPG算法原理
DDPG是Lillicrap等[14]將DQN算法應(yīng)用于連續(xù)動(dòng)作中而提出的一種基于確定性策略梯度的Actor-Critic框架無(wú)模型算法。DDPG的基本框架如圖4所示。
圖? 4? DDPG基本框架
Figure? 4.? Block diagram of DDPG
?
網(wǎng)絡(luò)整體采用了Actor-Critic形式,同時(shí)具備基于值函數(shù)的神經(jīng)網(wǎng)絡(luò)和基于策略梯度的神經(jīng)網(wǎng)絡(luò):Actor網(wǎng)絡(luò)的θπθπ表示確定性策略函數(shù)a=π(s|θπ)a=π(s|θπ),Critic網(wǎng)絡(luò)的θQθQ表示值函數(shù)Q(s,a|θQ)Q(s,a|θQ)。并且DDPG還借鑒了DQN技術(shù),其通過(guò)采取經(jīng)驗(yàn)池回放機(jī)制(experience replay)以及單獨(dú)的目標(biāo)網(wǎng)絡(luò)來(lái)消除大規(guī)模神經(jīng)網(wǎng)絡(luò)帶來(lái)的不穩(wěn)定性。
所謂經(jīng)驗(yàn)池回放機(jī)制,即在每個(gè)時(shí)間點(diǎn)都存儲(chǔ)當(dāng)前狀態(tài)、動(dòng)作等信息作為智能體的經(jīng)驗(yàn)et=(st,at,rt,st+1)et=(st,at,rt,st+1),以此形成回放記憶序列D={e1,?,eN}D={e1,?,eN}。在訓(xùn)練網(wǎng)絡(luò)時(shí),從中隨機(jī)提取mini batch數(shù)量的經(jīng)驗(yàn)數(shù)據(jù)作為訓(xùn)練樣本,但重復(fù)使用歷史數(shù)據(jù)的操作會(huì)增加數(shù)據(jù)的使用率,也打亂了原始數(shù)據(jù)的順序,會(huì)降低數(shù)據(jù)之間的關(guān)聯(lián)性。而目標(biāo)網(wǎng)絡(luò)則建立了2個(gè)結(jié)構(gòu)一樣的神經(jīng)網(wǎng)絡(luò)——用于更新神經(jīng)網(wǎng)絡(luò)參數(shù)的主網(wǎng)絡(luò)和用于產(chǎn)生優(yōu)化目標(biāo)值的目標(biāo)網(wǎng)絡(luò),初始時(shí),將主網(wǎng)絡(luò)參數(shù)賦予給目標(biāo)網(wǎng)絡(luò),然后主網(wǎng)絡(luò)參數(shù)不斷更新,目標(biāo)網(wǎng)絡(luò)不變,經(jīng)過(guò)一段時(shí)間后,再將主網(wǎng)絡(luò)的參數(shù)賦予給目標(biāo)網(wǎng)絡(luò)。此循環(huán)操作可使優(yōu)化目標(biāo)值在一段時(shí)間內(nèi)穩(wěn)定不變,從而使得算法性能更加穩(wěn)定。
在訓(xùn)練過(guò)程中,主網(wǎng)絡(luò)中的Actor網(wǎng)絡(luò)根據(jù)從經(jīng)驗(yàn)池中隨機(jī)選取的樣本狀態(tài)ss,經(jīng)過(guò)當(dāng)前策略函數(shù)a=π(s|θπ)a=π(s|θπ)選擇出最優(yōu)的動(dòng)作值aa交予船舶智能體,讓其與環(huán)境交互后得到下一時(shí)刻的狀態(tài)值s′s′。而此時(shí)的Critic網(wǎng)絡(luò)則接受當(dāng)前的狀態(tài)ss和動(dòng)作值aa,使用值函數(shù)Q(s,a|θQ)Q(s,a|θQ)評(píng)價(jià)當(dāng)前狀態(tài)的期望累計(jì)獎(jiǎng)賞,并用于更新Actor網(wǎng)絡(luò)的參數(shù)。在目標(biāo)網(wǎng)絡(luò)中,整體接收下一時(shí)刻的狀態(tài)s′s′,經(jīng)目標(biāo)Actor網(wǎng)絡(luò)選出動(dòng)作后交予目標(biāo)Critic獲得目標(biāo)期望值Q′(a′)Q′(a′),然后,再通過(guò)計(jì)算損失函數(shù)對(duì)主網(wǎng)絡(luò)的Critic網(wǎng)絡(luò)參數(shù)進(jìn)行更新。對(duì)于主網(wǎng)絡(luò)的Actor網(wǎng)絡(luò)參數(shù)更新,Silver等[15]證實(shí),確定性策略的目標(biāo)函數(shù)J(θπ)J(θπ)采用ππ策略的梯度與Q函數(shù)采用ππ策略的期望梯度是等價(jià)的:
|
?J(θπ)?θπ=Es[?Q(s,a|θQ)?θπ]?J(θπ)?θπ=Es[?Q(s,a|θQ)?θπ] |
(9) |
根據(jù)確定性策略a=π(s|θπ)a=π(s|θπ),得到Actor網(wǎng)絡(luò)的梯度為:
|
?J(θπ)?θπ=Es[?Q(s,a|θQ)?a?π(s|θπ)?θπ]?J(θπ)?θπ=Es[?Q(s,a|θQ)?a?π(s|θπ)?θπ] |
(10) |
|
?θπJ≈1N∑i(?aQ(s,a|θπ)|s=si,a=π(si)??θππ(s|θπ)|s=si)?θπJ≈1N∑i(?aQ(s,a|θπ)|s=si,a=π(si)??θππ(s|θπ)|s=si) |
(11) |
另一方面,對(duì)于Critic網(wǎng)絡(luò)中的價(jià)值梯度:
|
?L(θQ)?θQ=Es,a,r,s′~D[(TargetQ?Q(s,a|θQ))?Q(s,a|θQ)?θQ]?L(θQ)?θQ=Es,a,r,s′~D[(TargetQ?Q(s,a|θQ))?Q(s,a|θQ)?θQ] |
(12) |
|
TargetQ=r+γQ′(s′,π(s′|θπ′)|θQ′)TargetQ=r+γQ′(s′,π(s′|θπ′)|θQ′) |
(13) |
式中,θπ′θπ′和θQ′θQ′分別為目標(biāo)策略網(wǎng)絡(luò)和目標(biāo)值函數(shù)網(wǎng)絡(luò)的網(wǎng)絡(luò)參數(shù)。其中,目標(biāo)網(wǎng)絡(luò)的更新方法與DQN算法中的不同,在DDPG算法中,Actor-Critic網(wǎng)絡(luò)各自的目標(biāo)網(wǎng)絡(luò)參數(shù)是通過(guò)緩慢的變換方式更新,也叫軟更新。以此方式進(jìn)一步增加學(xué)習(xí)過(guò)程的穩(wěn)定性:
|
θQ′=τθQ+(1?τ)θQ′θQ′=τθQ+(1?τ)θQ′ |
(14) |
|
θπ′=τθπ+(1?τ)θπ′θπ′=τθπ+(1?τ)θπ′ |
(15) |
式中,ττ為學(xué)習(xí)率。
定義最小化損失函數(shù)來(lái)更新Critic網(wǎng)絡(luò)參數(shù),其中,yiyi為當(dāng)前時(shí)刻狀態(tài)動(dòng)作估計(jì)值函數(shù)與目標(biāo)網(wǎng)絡(luò)得到的目標(biāo)期望值間的誤差:
|
L=1N∑i(yi?Q(si,ai|θQ))2L=1N∑i(yi?Q(si,ai|θQ))2 |
(16) |
2.2?? 算法實(shí)現(xiàn)步驟
初始化Actor-Critic網(wǎng)絡(luò)的參數(shù),將當(dāng)前網(wǎng)絡(luò)的參數(shù)賦予對(duì)應(yīng)的目標(biāo)網(wǎng)絡(luò);設(shè)置經(jīng)驗(yàn)池容量為30 000個(gè),軟更新學(xué)習(xí)率為0.01,累計(jì)折扣系數(shù)設(shè)定為0.9,初始化經(jīng)驗(yàn)池。訓(xùn)練的每回合步驟如下:
1) 初始化船舶環(huán)境;
2) 重復(fù)以下步驟直至到達(dá)設(shè)置的最大步長(zhǎng);
3) 在主網(wǎng)絡(luò)中,Actor網(wǎng)絡(luò)獲取此刻船舶的狀態(tài)信息stst,并根據(jù)當(dāng)前的策略選取動(dòng)作舵令δtδt給船舶執(zhí)行,即δt=π(st|θπ)δt=π(st|θπ);
4) 船舶執(zhí)行當(dāng)前舵令后輸出獎(jiǎng)勵(lì)rtrt和下一個(gè)狀態(tài)st+1st+1,Actor網(wǎng)絡(luò)再次獲取該狀態(tài)信息并選取下一舵令δt+1δt+1;
5) 將此過(guò)程中產(chǎn)生的數(shù)據(jù)(st,δt,rt,st+1)(st,δt,rt,st+1)存儲(chǔ)在經(jīng)驗(yàn)池中,以作為網(wǎng)絡(luò)訓(xùn)練學(xué)習(xí)的數(shù)據(jù)集。當(dāng)經(jīng)驗(yàn)池存儲(chǔ)滿后,再?gòu)牡?個(gè)位置循環(huán)存儲(chǔ);
6) 從經(jīng)驗(yàn)池中隨機(jī)采樣N個(gè)樣本(st,δt,rt,st+1)(st,δt,rt,st+1),作為當(dāng)前Actor網(wǎng)絡(luò)和Critic網(wǎng)絡(luò)的訓(xùn)練數(shù)據(jù);
7) 通過(guò)損失函數(shù)更新Critic網(wǎng)絡(luò),根據(jù)Actor網(wǎng)絡(luò)的策略梯度更新當(dāng)前Actor網(wǎng)絡(luò),然后再對(duì)目標(biāo)網(wǎng)絡(luò)進(jìn)行相應(yīng)的軟更新。
3.?? 系統(tǒng)仿真與算法對(duì)比分析
3.1?? 仿真環(huán)境構(gòu)建
為驗(yàn)證上述方法的有效性,基于Python環(huán)境進(jìn)行了船舶航跡跟蹤仿真實(shí)現(xiàn)。控制研究對(duì)象模型選用文獻(xiàn)[16-17]中的單槳單舵7 m KVLCC2船模,建模采用三自由度模型(即縱蕩、橫蕩和艏搖),具體建模過(guò)程參考文獻(xiàn)[16]。表1列出了船舶的一些主要參數(shù)。
表? 1? KVLCC2船舶參數(shù)
Table? 1.? Parameters of a KVLCC2 tanker
| 參數(shù) | 數(shù)值 | ? | 參數(shù) | 數(shù)值 |
|---|---|---|---|---|
| 船長(zhǎng)Lpp/m | 7 | ? | 方形系數(shù)CbCb | 0.809 8 |
| 船寬Bwl/m | 1.168 8 | ? | 浮心坐標(biāo)/m | 0.244 0 |
| 型深D/m | 0.656 3 | ? | 螺旋槳直徑Dp/m | 0.216 0 |
| 排水體積/m3 | 3.272 4 | ? | 舵面積/m2 | 0.053 9 |
|?顯示表格
?
在所選用的DDPG控制器中,Crtic網(wǎng)絡(luò)和Actor網(wǎng)絡(luò)的實(shí)現(xiàn)參數(shù)設(shè)置分別如表2和表3所示。
表? 2? Critic網(wǎng)絡(luò)參數(shù)
Table? 2.? Critic network parameters
| 參數(shù) | 賦值 |
|---|---|
| 輸入層 | 狀態(tài)向量S(t)S(t) |
| 第1個(gè)隱層 | 300 |
| 第1層激活函數(shù) | Relu |
| 第2個(gè)隱層 | 200 |
| 第2層激活函數(shù) | Relu |
| 輸出層 | 動(dòng)作δ(t)δ(t) |
| 輸出層激活函數(shù) | Tanh |
| 參數(shù)初始化 | Xavier初始化 |
| 學(xué)習(xí)率 | 0.000 1 |
| 優(yōu)化器 | Adam |
?
?
表? 3? Actor網(wǎng)絡(luò)參數(shù)
Table? 3.? Actor network parameters
| 參數(shù) | 賦值 |
|---|---|
| 輸入層 | 狀態(tài)向量S(t)S(t),動(dòng)作δ(t)δ(t) |
| 第1個(gè)隱層 | 300 |
| 第1層激活函數(shù) | Relu |
| 第2個(gè)隱層 | 200 |
| 第2層激活函數(shù) | Relu |
| 輸出層 |
Q(S(i),δ(i))Q(S(i),δ(i)) |
| 輸出層激活函數(shù) | Linear |
| 參數(shù)初始化 | Xavier初始化 |
| 學(xué)習(xí)率 | 0.001 |
| 優(yōu)化器 | Adam |
?
3.2?? 控制器離線學(xué)習(xí)
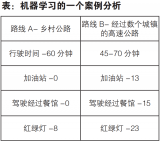
基于DDPG算法進(jìn)行的離線訓(xùn)練學(xué)習(xí)設(shè)置如下:初始化網(wǎng)絡(luò)參數(shù)以及經(jīng)驗(yàn)緩存池,設(shè)計(jì)最大的訓(xùn)練回合為2 000,每回合最大步長(zhǎng)為500,采樣時(shí)間為1 s。在規(guī)劃訓(xùn)練期間所需跟蹤的航跡時(shí),為使控制器適應(yīng)多種環(huán)境,以及考慮到LOS制導(dǎo)算法中對(duì)于航向控制的要求,依據(jù)文獻(xiàn)[18]中的設(shè)計(jì)思想,根據(jù)拐角的變換,設(shè)計(jì)了多條三航跡點(diǎn)航線,每回合訓(xùn)練時(shí)隨機(jī)選取一條進(jìn)行航跡跟蹤。
訓(xùn)練時(shí),將數(shù)據(jù)存入經(jīng)驗(yàn)池中,然后再?gòu)闹须S機(jī)采樣一組數(shù)據(jù)進(jìn)行訓(xùn)練,狀態(tài)值及動(dòng)作值均進(jìn)行歸一化處理,當(dāng)達(dá)到最大步長(zhǎng)或最終航跡點(diǎn)輸出完成時(shí),便停止這一回合,并計(jì)算當(dāng)前回合的總回報(bào)獎(jiǎng)勵(lì)。當(dāng)訓(xùn)練進(jìn)行到200,300和500回合時(shí),其航向誤差如圖5所示。由圖中可以看出,在訓(xùn)練時(shí)隨著回合的增加,航向誤差顯著減小,控制算法不斷收斂;當(dāng)訓(xùn)練達(dá)到最大回合結(jié)束后,總獎(jiǎng)勵(lì)值是不斷增加的。為使圖像顯示得更加清晰,截取了200~500回合的總回報(bào)獎(jiǎng)勵(lì)如圖6所示。從中可以看出,在約270回合時(shí)算法基本收斂,展現(xiàn)了快速學(xué)習(xí)的過(guò)程。
圖? 5? 航向誤差曲線
Figure? 5.? Course error curves
?
圖? 6? 總回報(bào)獎(jiǎng)勵(lì)曲線
Figure? 6.? Total reward curve
?
3.3?? 仿真實(shí)驗(yàn)設(shè)計(jì)及對(duì)比分析
上述訓(xùn)練完成后,DDPG控制器保存回報(bào)獎(jiǎng)勵(lì)函數(shù)最大的網(wǎng)絡(luò)參數(shù),并將其應(yīng)用于航跡跟蹤仿真。為了驗(yàn)證DDPG控制器的可行性,本文選用BP-PID控制器進(jìn)行對(duì)比分析。
用于對(duì)比的BP-PID控制器選擇使用輸入層節(jié)點(diǎn)數(shù)為4、隱含層節(jié)點(diǎn)數(shù)為5、輸出層節(jié)點(diǎn)數(shù)為3的BP神經(jīng)網(wǎng)絡(luò)對(duì)PID的3種參數(shù)進(jìn)行選擇,其中學(xué)習(xí)率為0.546,動(dòng)量因子為0.79,并參考文獻(xiàn)[19],利用附加慣性項(xiàng)對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行優(yōu)化。在相同的環(huán)境下,將DDPG控制器與BP-PID控制器進(jìn)行仿真對(duì)比分析。仿真時(shí),船舶的初始狀態(tài)為從原點(diǎn)(0,0)出發(fā),初始航向?yàn)?5°,初始航速也即縱蕩速度uu=1.179 m/s,螺旋槳初始速度rr=10.4 r/s。
仿真實(shí)驗(yàn)1:分別設(shè)計(jì)直線軌跡和鋸齒狀軌跡,用以觀察2種控制器對(duì)直線的跟蹤效果和面對(duì)劇烈轉(zhuǎn)角變化時(shí)的跟蹤效果(圖7),軌跡點(diǎn)坐標(biāo)分別為(0,50),(400,50)和(0,0),(100,250),(200,0),(300,250),(400,0),(500,250),(600,0),單位均為m。
?
圖? 7? 航跡跟蹤效果(實(shí)驗(yàn)1)
?
Figure? 7.? Tracking control result (experiment 1)
?
通過(guò)對(duì)2種類(lèi)型軌跡跟蹤的對(duì)比可以看出,對(duì)于直線軌跡,DDPG控制器能夠更加快速地進(jìn)行穩(wěn)定跟蹤,在鋸齒狀軌跡轉(zhuǎn)角跟蹤時(shí)其效果也明顯優(yōu)于BP-PID控制器。對(duì)仿真過(guò)程中航向角的均方根誤差(圖7(b))進(jìn)行計(jì)算,顯示BP-PID控制器的數(shù)值達(dá)61.017 8,而DDPG控制器的僅為10.018,后者具有更加優(yōu)秀的控制性能。
仿真實(shí)驗(yàn)2:為模擬傳統(tǒng)船舶的航行軌跡,設(shè)計(jì)軌跡點(diǎn)為(0,0),(100,50),(150,250),(400,250),(450,50),(550,0)的航跡進(jìn)行跟蹤。跟蹤效果曲線和航向均方根誤差(RMSE)的對(duì)比分別如圖8和表4所示。
圖? 8? 航跡跟蹤結(jié)果(實(shí)驗(yàn)2)
Figure? 8.? Tracking control result (experiment 2)
?
表? 4? 控制性能指標(biāo)
Table? 4.? Control performance
| 控制器 | RMSE |
|---|---|
| BP-PID控制器 | 13.585 0 |
| DDPG控制器 | 6.911 96 |
?
在此次仿真過(guò)程中,進(jìn)一步對(duì)比了2種控制器對(duì)于LOS角跟蹤的效果以及舵角的變化頻率,結(jié)果分別如圖9和圖10所示。PID經(jīng)過(guò)BP神經(jīng)網(wǎng)絡(luò)參數(shù)整定后整體巡航時(shí)間約為1 000 s,而DDPG控制器的巡航時(shí)間則在此基礎(chǔ)上縮短了4%;在轉(zhuǎn)角處的航向跟蹤中,DDPG控制器在20 s內(nèi)達(dá)到期望值,而B(niǎo)P-PID的調(diào)節(jié)時(shí)間則約為60 s,且控制效果并不穩(wěn)定,舵角振動(dòng)頻率高。由此可見(jiàn),深度強(qiáng)化學(xué)習(xí)控制器可以很快地根據(jù)航跡變化做出調(diào)整,減少了不必要的控制環(huán)節(jié),調(diào)節(jié)時(shí)間短,控制效果穩(wěn)定,舵角變化頻率小,具有良好的控制性能。
?
圖? 9? BP-PID控制器控制效果
?
Figure? 9.? Control result of BP-PID
?
?
圖? 10? DDPG控制器控制效果
Figure? 10.? Control result of DDPG
4.?? 結(jié) 語(yǔ)
本文針對(duì)船舶的航跡跟蹤問(wèn)題,提出了一種基于深度強(qiáng)化學(xué)習(xí)的航跡跟蹤控制器設(shè)計(jì)思路。首先根據(jù)LOS算法制導(dǎo),建立了航跡跟蹤控制的馬爾可夫模型,給出了基于DDPG控制器算法的程序?qū)崿F(xiàn);然后在Python環(huán)境中完成了船舶航跡跟蹤控制系統(tǒng)仿真實(shí)驗(yàn),并與BP-PID控制器進(jìn)行了性能對(duì)比分析。
將航跡跟蹤問(wèn)題進(jìn)行馬爾可夫建模設(shè)計(jì)后,將控制器投入離線學(xué)習(xí)。通過(guò)對(duì)此過(guò)程的分析發(fā)現(xiàn),DDPG控制器在訓(xùn)練中能快速收斂達(dá)到控制要求,證明了設(shè)計(jì)的狀態(tài)、動(dòng)作空間以及獎(jiǎng)勵(lì)函數(shù)的可行性。并且航跡跟蹤仿真對(duì)比結(jié)果也顯示,DDPG控制器能較快地應(yīng)對(duì)航跡變化,控制效果穩(wěn)定且舵角變化少,對(duì)于不同的軌跡要求適應(yīng)性均相對(duì)良好。整體而言,基于深度強(qiáng)化學(xué)習(xí)的控制方法可以應(yīng)用到船舶的航跡跟蹤控制之中,在具有自適應(yīng)穩(wěn)定控制能力的情況下,不僅免去了復(fù)雜的控制計(jì)算,也保證了實(shí)時(shí)性,對(duì)船舶的智能控制具有一定的參考價(jià)值。
?關(guān)注微信公眾號(hào):人工智能技術(shù)與咨詢。了解更多咨詢!
編輯:fqj
 電子發(fā)燒友App
電子發(fā)燒友App



















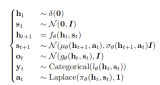
























評(píng)論