基于深度學習技術的電表大數(shù)據(jù)檢測系統(tǒng)
?來源:《?人工智能與機器人研究》?,作者方向
摘要:?隨著我國電廠不斷發(fā)展,我國智能電表裝機量不斷擴大,日臻成熟,對智能電表的監(jiān)測越來越重要。本文通過對電表數(shù)據(jù)的采集、清洗,完成數(shù)據(jù)格式化。運用皮爾森相關系數(shù)分析以及K折交叉驗證等方法,進行數(shù)據(jù)分析。通過采用深度學習時序模型進行預測研究,最終達到檢測電表運行狀態(tài)的目的。通過利用智能電表大數(shù)據(jù)對電表運行狀態(tài)的分析,可以判斷電表運行是否正常,如果異常是屬于故障還是有偷漏電發(fā)生,判斷相關位置,以便進一步采取行動。該檢測系統(tǒng)的研究與應用,可以避免智能電表的物理檢測,可以達到延長正常電表的使用壽命,節(jié)省大量的資源的目的。
1. 引言
智能電網(wǎng)的基礎是高速雙向智能通信網(wǎng)絡。通過傳感測量、控制技術等實現(xiàn)高效、安全的電網(wǎng)運行,保證電網(wǎng)的智能化建設 [1]。智能電表作為智能電網(wǎng)的重要部分,主要涉及以下部分:測量、通信、數(shù)據(jù)處理單元等 [2],是一種智能化儀表,能夠有效地測量電力參數(shù)、計量雙向電能 [3],能夠實現(xiàn)實時數(shù)據(jù)交互,對電能的質量進行監(jiān)測,實施遠程監(jiān)控。
智能電表中使用了諸多新的科學技術,突破了電子式表的發(fā)展,以智能芯片作為核心,集成數(shù)據(jù)庫、讀表器以及操作系統(tǒng)等,通過計算機通信平臺,實現(xiàn)自動化的電力計量和計費,更加快捷便利 [4]。智能電表是智能電網(wǎng)的智能終端和數(shù)據(jù)入口,為了適應智能電網(wǎng),智能電表具有雙向多種費率計量、用戶端實時控制、多種數(shù)據(jù)傳輸模式、智能交互等多種應用功能。智能電網(wǎng)建設為全球智能電表及用電信息采集、處理系統(tǒng)產品帶來了廣闊的市場需求 [5] [6]。預計到2020年全球將安裝近20億臺智能電表,智能電網(wǎng)將覆蓋全世界80%的人口,智能電表滲透率達到60% [7]。
目前國家規(guī)定的智能電表使用年限一般為8年,但實際上在智能電表使用8年后,大部分可以正常使用,而以前采用的物理檢測方式使拆下的電表基本全部更換了。如果可以只對異常電表進行更換,則可以為國家和個人節(jié)省巨大的每年高達百億以上的經濟成本。本次研究的目的是根據(jù)采集的用電小區(qū)的用電數(shù)據(jù),對其進行數(shù)據(jù)分析,以期在不對電表進行物理處置的情況下通過挖掘出用戶電表的異常信息,發(fā)現(xiàn)存在異常的電表 [8],為不拆電表進行物理檢測提供相關依據(jù)與方法。
2. 數(shù)據(jù)分析與處理
2.1. 數(shù)據(jù)整理與分析
2.1.1. 解決問題的思路
本文研究的主要目的是根據(jù)電表的數(shù)據(jù)預測分析電表是否異常,異常的情況包括故障或者偷漏電等。
目前國內也有一些相關方面的研究已經或正在進行。其中有通過分析不同用戶的電力消費類型,得出不同時間類型下的用戶消費模型差異。利用支持向量機理論,來檢測用電異常。這種方法所需訓練時間較少,無需對人工異常數(shù)據(jù)進行分類,能有效降低方案的應用成本 [9]。
還有基于受攻擊的智能電表CPU利用率和網(wǎng)絡通信流量異常上升,提出AMI中基于大數(shù)據(jù)的檢測方法。由各智能電表記錄其CPU負荷率及網(wǎng)絡通信流量,將此數(shù)據(jù)與電量功率數(shù)據(jù)一起上傳到用電管理中心數(shù)據(jù)服務器,再由異常甄別系統(tǒng)對相同型號智能電表的CPU負荷率及網(wǎng)絡通信流量進行對比,即可利用大量表計數(shù)據(jù)的統(tǒng)計特性,識別出CPU負荷率和通信流量明顯偏高的異常電表 [10]。
國外針對智能電表端的研究進行得較為深入,目前主要在竊電、惡意軟件檢測等方面。
Babu V,Nicol D M等針對惡意代碼在AMI網(wǎng)絡中的傳播問題,提出了在網(wǎng)絡層和應用層部署新的協(xié)議,通過對報文語義和語法的檢查,使得惡意代碼的檢測精度達到了99.72%至99.96% [11]。
Depuru S S R等通過對電力數(shù)據(jù)分類,利用SVM方法訓練樣本,使得對該樣本的檢測精度達到了98.4%。
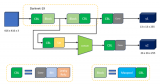
智能電網(wǎng)的信息采集和量測主要是在量測設備上進行采集和匯總,主要包括電網(wǎng)狀態(tài)量測系統(tǒng)和個人用戶量測系統(tǒng)兩類。如圖1所示 [12]。
?
?
Figure 1. Smart grid testing system classification
圖1. 智能電網(wǎng)量測系統(tǒng)分類
針對本項目小區(qū)電表的研究,在數(shù)據(jù)方面的處理應遵循:1) 通過特征工程各種方法,盡可能提取影響電表誤差的特征;2) 通過特征和誤差的關系建立回歸模型,預測測試集中一個點/一段時間的誤差,結論為誤差是否在電表正常范圍內,不在正常范圍則判斷小區(qū)電表是否有異常存在;3) 如存在異常電表,則根據(jù)單電表的用電特性行為模型,找出異常電表的存在。
2.1.2. 數(shù)據(jù)格式設置
針對獲取的小區(qū)電表數(shù)據(jù),設定相關參數(shù)如下:
每15分鐘的小區(qū)總表電壓U_super_15;
每15分鐘的小區(qū)總表電流I_super_15;
每60分鐘的用戶表電壓U_sub_60;
每60分鐘的用戶表電流I_sub_60;
每24小時用戶表電量W_sub;
每24小時小區(qū)總表電量W_super;
總表與用戶表總和之差為E。
?
UI與電量表比較得到誤差E,時間粒度為一天。
2.1.3. 數(shù)據(jù)清洗
通過誤差(總表–分表和)曲線圖2發(fā)現(xiàn),數(shù)據(jù)中存在兩類錯誤值:重復值和非法值。
觀察數(shù)據(jù),發(fā)現(xiàn)分表與總表的分時電流電壓精度不同,分表出現(xiàn)大量缺失值。采取的解決辦法為用整點電流電壓代替缺失值。最終,通過刪除錯誤值,填補缺失值完成數(shù)據(jù)清洗。
?
?
Figure 2. Huayuan community error curve
圖2. 花園小區(qū)誤差曲線
2.1.4. 數(shù)據(jù)特性分析
通過繪制電量曲線如圖3所示,選取較為理想的數(shù)據(jù)。經過分析,認定花園小區(qū)2016年數(shù)據(jù)及東輝花園全部數(shù)據(jù)較為理想。
?
?
Figure 3. Electric quantity of Huayuan community
圖3. 花園小區(qū)電量曲線
為了分析誤差與電量的關系,繪制了總表與分表和散點圖如圖4所示、絕對誤差曲線圖如圖5所示以及相對誤差曲線圖如圖6所示。
隨后對誤差的分布進行分析。下圖分別為花園小區(qū)2016.1.1~3.1誤差分布如圖7所示、2016.3.1~5.1誤差分布如圖8所示、2016.5.1~7.1誤差分布如圖9所示以及2016.1.1~2016.7.1誤差分布如圖10所示。
?
?
Figure 4. Sub total & super of Huayuan community
圖4. 花園小區(qū)總表與分表和
?
?
圖10. 2016.1.1~7.1誤差分布
經過分析發(fā)現(xiàn),誤差基本呈正態(tài)分布,但是分布并不固定,無法通過觀察分布來確定異常點。
2.2. 數(shù)據(jù)進一步處理
2.2.1. 數(shù)據(jù)格式化
為便于進行機器學習分析,數(shù)據(jù)的每個日期增加了以下特征如表1所示。
|
特征 |
解釋 |
|
總表數(shù)據(jù)(super) |
總表的電流值 |
|
誤差(error) |
總表–分表和 |
|
相對日期(com_date) |
以某日為基準0,與基準日相差的天數(shù) |
|
周(week) |
歸一化為7維向量 |
|
月(month) |
歸一化為12維向量 |
|
年(year) |
歸一化為3維向量 |
|
對數(shù)值(log) |
總表以2為底的對數(shù)值 |
|
戶數(shù)(numbers) |
當日的總戶數(shù) |
|
平均電流(A_mean) |
當日平均電流 |
|
平均電壓(V_mean) |
當日平均電壓 |
Table 1. Add data characteristics
表1. 增加數(shù)據(jù)特征
2.2.2. 皮爾森相關系數(shù)分析
為了給予機器學習更多方向性建議,對每個維度之間進行了相關系數(shù)分析 [13]。
2.2.3. K折交叉驗證
對數(shù)據(jù)采取5折交叉驗證方式,即將五分之一的數(shù)據(jù)用于測試,其余數(shù)據(jù)用于訓練,可以得到五組不同的訓練集與測試集 [14]。
3. 特征工程與擬合
3.1. 數(shù)據(jù)可靠性分析
得到的數(shù)據(jù)后需要對其可靠性進行分析。首先挑選花園小區(qū)中不同用戶分析在同一時間段內同一時間的電壓情況。經過分析發(fā)現(xiàn)在同一時刻,不同戶數(shù)的電壓情況是大致一致的,而且根據(jù)不同的日期,電壓的變化趨勢也及其相似。
接著再分析電流變化的情況。隨機選取一個用戶的電表,繪制其于不同時刻電流的折線圖如圖11所示。藍線代表著凌晨3點,橙線代表清晨6點,而綠線代表下午6點。可以看出,3點是電流數(shù)值于三者中最低,而上午6點時有所升高,在下午6點時達到最高。可以理解是因為凌晨3點時用電量極低,大多數(shù)人都在睡眠,而下午6點用電逐漸增多。
?
?
Figure 11. Electricity consumption of same user
圖11. 同一用戶的用電情況
而這三條線在八月份時候整體變高,而且差距變小,則說明可能是因為八月份是夏天最熱的時候,氣溫溫度上升,用戶開始頻繁使用空調導致用電增加,而在夜間也保持空調處于打開狀態(tài)。從而可以解釋在八月份三個時間點的電流情況相差不多的原因。
隨后以0.2 A作為標準,超過0.2 A即認為該用戶處于用電狀態(tài)。繪制0點到24點用電戶數(shù)的圖表如圖12所示。由圖可知,6點和18點的確用電人數(shù)較多,而凌晨3點較少,說明先前假設正確。
?
?
Figure 12. Number of users in different time at same day
圖12. 同一天內不同時間用電戶數(shù)
3.2. 異常點分析
數(shù)據(jù)中的異常值需要額外關注。如果不剔除異常值進行計算分析,往往會對結果帶來不利影響。可以利用箱體圖來識別數(shù)據(jù)批中的異常值,用python繪制用戶關于電壓的箱體圖 [15]。全部用戶5個月內的電壓的箱體圖如圖13所示。可以發(fā)現(xiàn)0點到6點之間異常點極少,而之后由于可能存在重疊問題,所以是否屬于異常點過多的情況較難判斷。
?
?
Figure 13. Voltage box diagram
圖13. 電壓箱體圖
電流的箱體圖如圖14所示,但是發(fā)現(xiàn)異常點都處于箱體的上方。因為大多數(shù)時間很多電器處于關閉狀態(tài),所以導致均值較低,更容易在上方產生異常點。正是利用圖14確定了用0.2 A作為判斷用戶是否用電的標準。
?
?
Figure 14. Current box diagram
圖14. 電流箱體圖
3.3. 多項式擬合
利用公式?W=U?I?tW=U?I?t?然后求和,可以得到有分戶計算出來的電量值。再用總表測得的電量值與之相減,便可得到電量測定的誤差值。利用poly0fit對先前求得的誤差值進行擬合,并繪制曲線 [16] [17]。數(shù)據(jù)選取時間間隔為連續(xù)7個月209天。通過改變多項式最高項次數(shù)可以做出不同的擬合圖,下面兩幅圖是最高次冪分別為4和8的擬合圖,如圖15、圖16所示。由4到8擬合程度提高明顯,而實驗證實最高次冪由8提高到10的效果不太明顯。
?
?
?
Figure 16. Fitting with the highest power of 8
圖16. 最高次冪為8的擬合
4. 深度學習時序模型
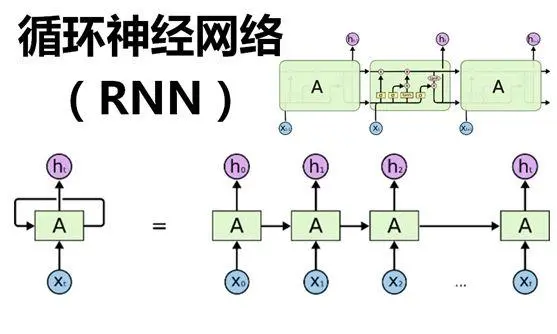
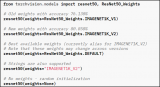
基于前面的分析,為發(fā)現(xiàn)總表測量和分表和的誤差的時序性,使用了一些模型來體現(xiàn)數(shù)據(jù)中年份和四季帶來的波動。模型主要依靠的信息源有兩類:局部特征和全局特征。長短時記憶(LSTM)循環(huán)神經網(wǎng)絡作為RNN的一個重要變體,幾乎可以無縫建模具備多個輸入變量的問題,這為時間序列預測帶來極大益處,因為經典線性方法難以適應多變量或多輸入預測問題。可以在Tensorflow和Keras深度學習庫中搭建用于多變量時間序列預測的LSTM模型。
最近研究發(fā)現(xiàn),LSTM模型在處理時序問題時有一定優(yōu)勢:因為其基于過去值和過去值的預測值來預測未來值而不是僅僅使用季節(jié)等離散不相關特征,使用過去值的預測值能使模型更加穩(wěn)定。訓練過程中每一步的錯誤都會累積,當某一步出現(xiàn)了極端錯誤,可能就會毀壞其后面所有時步的預測質量 [18] [19]。
深度學習時序模型的工作包括:1) 將原始數(shù)據(jù)集轉換成適用于時間序列預測的數(shù)據(jù)集;2) 處理數(shù)據(jù)并使其適應用于多變量時間序列預測問題的LSTM模型;3) 做出預測并分析結果。
4.1. 時序數(shù)據(jù)預處理
經過之前的特征工程和數(shù)據(jù)處理,已經提取了數(shù)據(jù)中許多與誤差相關的變量,這是因為RNN本身在特征提取上已足夠強大。本模型使用的特征和數(shù)據(jù)類型如表2所示。
|
特征 |
解釋 |
|
“sub”: “float” |
單元用戶分表和電量 |
|
“super”: “float” |
總表電量測量值,實際x只取super和sub其一以保證模型的泛化能力 |
|
“error”: “float” |
總表與分表和相減得到電表的電量測量誤差,本模型用做y值,其他特征為x值 |
|
“com_date”: “int” |
相對天數(shù),原始數(shù)據(jù)的第一天設為0,之后每天遞增 |
|
“week”: “l(fā)ist” |
時間特征向量,7維one-hot編碼; |
|
“month”: “l(fā)ist” |
時間特征向量,12維one-hot編碼; |
|
“year”: “l(fā)ist” |
時間特征向量,3維one-hot編碼; |
|
“numbers”: “int” |
用電戶數(shù),因為3年里戶數(shù)有變化(新搬入用戶和搬出等) |
Table 2. Deep learning time model characteristics and data type
表2. 深度學習時序模型特征與數(shù)據(jù)類型
所有特征(包括one-hot編碼的特征,包括x和y)都正則化成均值為零、單位方差的數(shù)據(jù),每一個特征序列都是對本列單獨正則化的。常用的正則化方法有標準化和最大值正則化。標準化Standardization是指將特征數(shù)據(jù)的分布調整成標準正太分布,也叫高斯分布,也就是使得數(shù)據(jù)的均值為0,方差為1。標準化的原因在于如果有些特征的方差過大,則會主導目標函數(shù)從而使參數(shù)估計器無法正確地去學習其他特征。最大值正則化MaxAbsScaler使得特征分布是在一個給定最小值和最大值的范圍內的。一般情況下是在[0, 1]之間。最大值正則化是專門為稀疏數(shù)據(jù)的規(guī)模化所設計的。之后的實驗中也驗證了標準化,不做正則化和最值正則化的情況。實驗發(fā)現(xiàn)標準化Standardization有時會產生負數(shù),在訓練和數(shù)據(jù)分析時需要額外注意 [20] [21]。
模型從原始時間序列上隨機抽取固定長度的樣本進行訓練。例如,如果原始時間序列的長度為600天,那么把訓練樣本的時間步長設為200天,就可以有400種不同的起始點。這種采樣方法相當于一種有效的數(shù)據(jù)增強機制。在每一步訓練中,訓練程序都會隨機選擇時序的開始點,相當于生成了無限長的、幾乎不重復的訓練數(shù)據(jù)。時間步長是本模型中重要的超參數(shù),在學習序列預測問題時,LSTM通過時間步進行反向傳播。之后可以為LSTM模型準備專用的時序數(shù)據(jù)集,這會涉及將數(shù)據(jù)集用作監(jiān)督學習問題。監(jiān)督學習問題可以設定為:1) 根據(jù)上一個時間段的總表和其他輸入,預測當前時刻(t)的電表誤差;2) 根據(jù)過去一天的電表情況以及下一個小時的預測情況,預測再下一個小時的電表誤差情況。
在所有5年數(shù)據(jù)中,僅使用第1年的數(shù)據(jù)來擬合模型,然后用其余4年的數(shù)據(jù)進行評估。1) 將數(shù)據(jù)集分成訓練集和測試集;2) 將訓練集和測試集分別分成輸入和輸出變量;3) 將輸入(X)重構為LSTM預期的3D格式,即[樣本量,時間步,特征]。
4.2. 時序問題數(shù)據(jù)訓練
時序問題中,劃分訓練集和驗證集的方法有兩種如圖17所示。
?
?
Figure 17. Classification of training set and verifying set
圖17. 訓練集和驗證集的劃分方法
4.2.1. Walk-Forward Split方法
Walk-forward split方法事實上不是真的在劃分數(shù)據(jù)。它的數(shù)據(jù)集的全集同時作為訓練集和驗證集,但驗證集用了不同的時間表。相比訓練集的時間表,驗證集的時間表被調前了一個預測間隔期。
4.2.2. Side-by-Side Split方法
Side-by-side split方法是一種主流的劃分方式,將數(shù)據(jù)集切分為獨立的不同子集,一部分完全用于訓練,另一部分完全用于驗證。
Walk-forward split方法的結果更可觀,比較符合研究的最終目標:用歷史值預測未來值。但這種切分方法有其弊端,因為它需要在時間序列末端使用完全只用作預測的數(shù)據(jù)點,這樣在時間序列上訓練的數(shù)據(jù)點和預測的數(shù)據(jù)點間隔較長,想要準確預測未來的數(shù)據(jù)就會變得困難。假如有300天的歷史數(shù)據(jù),想要預測接下來的100天。如果選擇Walk-forward split劃分方法,則會使用第前100天作為訓練數(shù)據(jù),接下來100天作為訓練過程中的預測數(shù)據(jù),接下來100天的數(shù)據(jù)用作驗證集。所以也就是實際上用了1/3的數(shù)據(jù)點在訓練,在最后一次訓練數(shù)據(jù)點和第一次預測數(shù)據(jù)點之間有200天的間隔。這個間隔較長,所以一旦離開訓練的場景,預測質量會顯著下降。如果只有100天的間隔,預測質量會有顯著提升。Side-by-side split方法在末端序列上不會單獨耗用數(shù)據(jù)點作為預測的數(shù)據(jù)集,但模型在驗證集上的性能就會和訓練集的性能有很強的關聯(lián)性,卻與未來要預測的真實數(shù)據(jù)沒有任何相關性,所以,這樣劃分數(shù)據(jù)沒有實質性作用,只是重復了在訓練集上觀察到的模型損失。
本模型中使用walk-forward split方法劃分的驗證集只是用來調優(yōu)參數(shù),最后的預測模型必然是在與訓練集和驗證集完全無相關的數(shù)據(jù)下運行的。
實際研究是將在第一個隱藏層中定義具有40個神經元的LSTM,在輸出層中定義1個用于預測誤差的神經元。輸入數(shù)據(jù)維度將是1個具有22個特征的時間步長為40天的樣本。
實際研究中使用了均方根誤差(RMSE)損失函數(shù)和高效的隨機梯度下降的Adam版本。該模型將適用于1000個epoch,大小為128的訓練。選擇epoch的數(shù)目時,因為不清楚模型訓練到哪一步是最適合用于預測未來值的(因為基于當前數(shù)據(jù)的驗證集和未來數(shù)據(jù)的關聯(lián)性很弱),所以不能過早停止訓練。經過實驗最終選用1000作為epoch的數(shù)目。
模型擬合后,可以預測整個測試數(shù)據(jù)集。將預測與測試數(shù)據(jù)集相結合,并調整測試數(shù)據(jù)集的規(guī)模。還使用了預期的誤差來調整測試數(shù)據(jù)集的規(guī)模。通過初始預測值和實際值,可以計算模型的誤差分數(shù)。在這種情況下,可以計算出與變量相同的單元誤差的均方根誤差(RMSE)。RMSE是常用的回歸問題的損失函數(shù),不同于交叉熵損失適用于分類問題,在本問題中它可以快速得到損失并且得到的結果每一處都很平滑。
4.3. 結果分析與異常檢測
實驗測試了雙層LSTM和單層LSTM的預測結果,隱層單元數(shù)量分別為20和40。結果如圖18和圖19所示。
?
?
Figure 18. Predicted value and real value of LSTM model
圖18. LSTM模型預測值與真實值
?
?
Figure 19. Scatter diagram of LSTM model
圖19. LSTM模型散點圖
時間維度上的預測值和真實值比較,可以看到最初幾步的預測較為準確,同時可以發(fā)現(xiàn)預測值有一定的滯后。散點圖中,越靠近y = x直線表示模型預測越準確。
用滑窗進行異常檢測,設置一個寬度為l的滑窗,假設閾值為t。
對于每一次滑動:如果窗口內每一個預測值與實際值之差都超過閾值,則認為從這一天開始出現(xiàn)誤差。當窗口寬度為4,閾值為0.5時,結果如圖20所示。即第65天開始,數(shù)據(jù)出現(xiàn)可以檢測的異常,通過對寬度與閾值的調整,可以得到更高精度的結果。
當數(shù)據(jù)沒有異常時,結果如圖21所示。
?
?
Figure 20. Abnormal date of calculation
圖20. 計算出的異常相對日期
?
?
Figure 21. Predicated value within range
圖21. 預測值在范圍之內
5. 結論
本文所介紹的基于深度學習模型的對預測檢測電表是否異常的方法是行之有效的。隨著我國智能電表的普及與應用,在更多大數(shù)據(jù)的支持下,對智能電表的預測檢測會更加準確,也可以在未來使我國智能電表在使用周期壽命到達后可以不拆表進行相關檢測,保證無故障電表繼續(xù)正常使用,從而使電表的實際使用壽命有所增加,從而節(jié)省大量的資源。
?審核編輯:符乾江
 電子發(fā)燒友App
電子發(fā)燒友App





















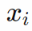












評論