特征選擇方法初識(shí)：

1、為什么要做特征選擇
在有限的樣本數(shù)目下，用大量的特征來設(shè)計(jì)分類器計(jì)算開銷太大而且分類性能差。

2、特征選擇的確切含義
將高維空間的樣本通過映射或者是變換的方式轉(zhuǎn)換到低維空間，達(dá)到降維的目的，然后通過特征選取刪選掉冗余和不相關(guān)的特征來進(jìn)一步降維。

3、特征選取的原則
獲取盡可能小的特征子集，不顯著降低分類精度、不影響類分布以及特征子集應(yīng)具有穩(wěn)定適應(yīng)性強(qiáng)等特點(diǎn)

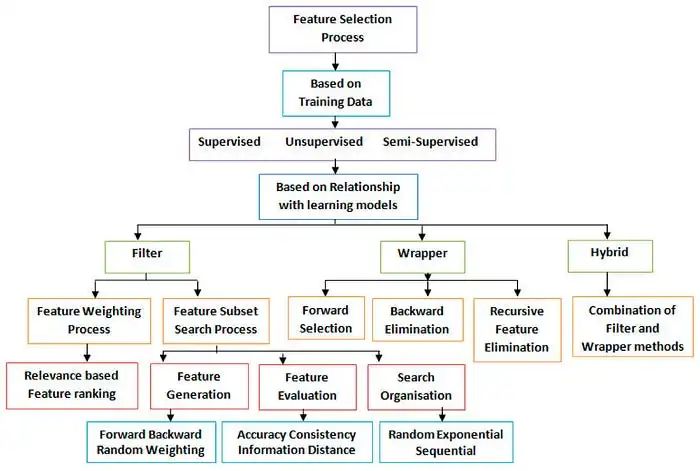
主要有三種方法：

?

1、Filter方法

其主要思想是：對(duì)每一維的特征“打分”，即給每一維的特征賦予權(quán)重，這樣的權(quán)重就代表著該維特征的重要性，然后依據(jù)權(quán)重排序。

主要的方法有：

• Chi-squared test(卡方檢驗(yàn))

• information gain(信息增益)

• correlation coefficient scores(相關(guān)系數(shù))

?

2、Wrapper方法

其主要思想是：將子集的選擇看作是一個(gè)搜索尋優(yōu)問題，生成不同的組合，對(duì)組合進(jìn)行評(píng)價(jià)，再與其他的組合進(jìn)行比較。這樣就將子集的選擇看作是一個(gè)是一個(gè)優(yōu)化問題，這里有很多的優(yōu)化算法可以解決，尤其是一些啟發(fā)式的優(yōu)化算法，如GA，PSO，DE，ABC等。

主要方法有：(遞歸特征消除算法)

3、Embedded方法

其主要思想是：在模型既定的情況下學(xué)習(xí)出對(duì)提高模型準(zhǔn)確性最好的屬性。這句話并不是很好理解，其實(shí)是講在確定模型的過程中，挑選出那些對(duì)模型的訓(xùn)練有重要意義的屬性。

簡單易學(xué)的機(jī)器學(xué)習(xí)算法——嶺回歸(Ridge Regression)”，嶺回歸就是在基本線性回歸的過程中加入了正則項(xiàng)。

總結(jié)以及注意點(diǎn)

這篇文章中最后提到了一點(diǎn)就是用特征選擇的一點(diǎn)Trap。個(gè)人的理解是這樣的，特征選擇不同于特征提取，特征和模型是分不開，選擇不同的特征訓(xùn)練出的模型是不同的。在機(jī)器學(xué)習(xí)=模型+策略+算法的框架下，特征選擇就是模型選擇的一部分，是分不開的。這樣文章最后提到的特征選擇和交叉驗(yàn)證就好理解了，是先進(jìn)行分組還是先進(jìn)行特征選擇。

答案是當(dāng)然是先進(jìn)行分組，因?yàn)榻徊骝?yàn)證的目的是做模型選擇，既然特征選擇是模型選擇的一部分，那么理所應(yīng)當(dāng)是先進(jìn)行分組。如果先進(jìn)行特征選擇，即在整個(gè)數(shù)據(jù)集中挑選擇機(jī)，這樣挑選的子集就具有隨機(jī)性。

我們可以拿正則化來舉例，正則化是對(duì)權(quán)重約束，這樣的約束參數(shù)是在模型訓(xùn)練的過程中確定的，而不是事先定好然后再進(jìn)行交叉驗(yàn)證的。

特征選擇方法具體分細(xì)節(jié)總結(jié)：

1 去掉取值變化小的特征 Removing features with low variance
該方法一般用在特征選擇前作為一個(gè)預(yù)處理的工作，即先去掉取值變化小的特征，然后再使用其他的特征選擇方法選擇特征。

2 單變量特征選擇 Univariate feature selection
單變量特征選擇能夠?qū)γ恳粋€(gè)特征進(jìn)行測試，衡量該特征和響應(yīng)變量之間的關(guān)系，根據(jù)得分扔掉不好的特征。對(duì)于回歸和分類問題可以采用卡方檢驗(yàn)等方式對(duì)特征進(jìn)行測試。

2.1 Pearson相關(guān)系數(shù) Pearson Correlation
皮爾森相關(guān)系數(shù)是一種最簡單的，能幫助理解特征和響應(yīng)變量之間關(guān)系的方法，該方法衡量的是變量之間的線性相關(guān)性，結(jié)果的取值區(qū)間為[-1，1]，-1表示完全的負(fù)相關(guān)(這個(gè)變量下降，那個(gè)就會(huì)上升)，+1表示完全的正相關(guān)，0表示沒有線性相關(guān)。

2.2 互信息和最大信息系數(shù) Mutual information and maximal information coefficient (MIC)
以上就是經(jīng)典的互信息公式了。想把互信息直接用于特征選擇其實(shí)不是太方便：1、它不屬于度量方式，也沒有辦法歸一化，在不同數(shù)據(jù)及上的結(jié)果無法做比較；2、對(duì)于連續(xù)變量的計(jì)算不是很方便（X和Y都是集合，x，y都是離散的取值），通常變量需要先離散化，而互信息的結(jié)果對(duì)離散化的方式很敏感。

2.3 距離相關(guān)系數(shù) (Distance correlation)
距離相關(guān)系數(shù)是為了克服Pearson相關(guān)系數(shù)的弱點(diǎn)而生的。Pearson相關(guān)系數(shù)是0，我們也不能斷定這兩個(gè)變量是獨(dú)立的（有可能是非線性相關(guān)）；但如果距離相關(guān)系數(shù)是0，那么我們就可以說這兩個(gè)變量是獨(dú)立的。

2.4 基于學(xué)習(xí)模型的特征排序 (Model based ranking)
這種方法的思路是直接使用你要用的機(jī)器學(xué)習(xí)算法，針對(duì)每個(gè)單獨(dú)的特征和響應(yīng)變量建立預(yù)測模型。其實(shí)Pearson相關(guān)系數(shù)等價(jià)于線性回歸里的標(biāo)準(zhǔn)化回歸系數(shù)。假如某個(gè)特征和響應(yīng)變量之間的關(guān)系是非線性的，可以用基于樹的方法（決策樹、隨機(jī)森林）、或者擴(kuò)展的線性模型等。基于樹的方法比較易于使用，因?yàn)樗麄儗?duì)非線性關(guān)系的建模比較好，并且不需要太多的調(diào)試。但要注意過擬合問題，因此樹的深度最好不要太大，再就是運(yùn)用交叉驗(yàn)證。

3 線性模型和正則化
單變量特征選擇方法獨(dú)立的衡量每個(gè)特征與響應(yīng)變量之間的關(guān)系，另一種主流的特征選擇方法是基于機(jī)器學(xué)習(xí)模型的方法。有些機(jī)器學(xué)習(xí)方法本身就具有對(duì)特征進(jìn)行打分的機(jī)制，或者很容易將其運(yùn)用到特征選擇任務(wù)中，例如回歸模型，SVM，決策樹，隨機(jī)森林等等。

3.1 正則化模型
正則化就是把額外的約束或者懲罰項(xiàng)加到已有模型（損失函數(shù)）上，以防止過擬合并提高泛化能力。損失函數(shù)由原來的E(X,Y)變?yōu)镋(X,Y)+alpha||w||，w是模型系數(shù)組成的向量（有些地方也叫參數(shù)parameter，coefficients），||·||一般是L1或者L2范數(shù)，alpha是一個(gè)可調(diào)的參數(shù)，控制著正則化的強(qiáng)度。當(dāng)用在線性模型上時(shí)，L1正則化和L2正則化也稱為Lasso和Ridge。

3.2 L1正則化/Lasso
L1正則化將系數(shù)w的l1范數(shù)作為懲罰項(xiàng)加到損失函數(shù)上，由于正則項(xiàng)非零，這就迫使那些弱的特征所對(duì)應(yīng)的系數(shù)變成0。因此L1正則化往往會(huì)使學(xué)到的模型很稀疏（系數(shù)w經(jīng)常為0），這個(gè)特性使得L1正則化成為一種很好的特征選擇方法。

3.3 L2正則化/Ridge regression
L2正則化將系數(shù)向量的L2范數(shù)添加到了損失函數(shù)中。由于L2懲罰項(xiàng)中系數(shù)是二次方的，這使得L2和L1有著諸多差異，最明顯的一點(diǎn)就是，L2正則化會(huì)讓系數(shù)的取值變得平均。對(duì)于關(guān)聯(lián)特征，這意味著他們能夠獲得更相近的對(duì)應(yīng)系數(shù)。還是以Y=X1+X2為例，假設(shè)X1和X2具有很強(qiáng)的關(guān)聯(lián)，如果用L1正則化，不論學(xué)到的模型是Y=X1+X2還是Y=2X1，懲罰都是一樣的，都是2alpha。但是對(duì)于L2來說，第一個(gè)模型的懲罰項(xiàng)是2alpha，但第二個(gè)模型的是4*alpha。可以看出，系數(shù)之和為常數(shù)時(shí)，各系數(shù)相等時(shí)懲罰是最小的，所以才有了L2會(huì)讓各個(gè)系數(shù)趨于相同的特點(diǎn)。
可以看出，L2正則化對(duì)于特征選擇來說一種穩(wěn)定的模型，不像L1正則化那樣，系數(shù)會(huì)因?yàn)榧?xì)微的數(shù)據(jù)變化而波動(dòng)。所以L2正則化和L1正則化提供的價(jià)值是不同的，L2正則化對(duì)于特征理解來說更加有用：表示能力強(qiáng)的特征對(duì)應(yīng)的系數(shù)是非零

4 隨機(jī)森林
隨機(jī)森林具有準(zhǔn)確率高、魯棒性好、易于使用等優(yōu)點(diǎn)，這使得它成為了目前最流行的機(jī)器學(xué)習(xí)算法之一。隨機(jī)森林提供了兩種特征選擇的方法：mean decrease impurity和mean decrease accuracy。

4.1 平均不純度減少 mean decrease impurity
隨機(jī)森林由多個(gè)決策樹構(gòu)成。決策樹中的每一個(gè)節(jié)點(diǎn)都是關(guān)于某個(gè)特征的條件，為的是將數(shù)據(jù)集按照不同的響應(yīng)變量一分為二。利用不純度可以確定節(jié)點(diǎn)（最優(yōu)條件），對(duì)于分類問題，通常采用基尼不純度或者信息增益，對(duì)于回歸問題，通常采用的是方差或者最小二乘擬合。當(dāng)訓(xùn)練決策樹的時(shí)候，可以計(jì)算出每個(gè)特征減少了多少樹的不純度。對(duì)于一個(gè)決策樹森林來說，可以算出每個(gè)特征平均減少了多少不純度，并把它平均減少的不純度作為特征選擇的值。

4.2 平均精確率減少 Mean decrease accuracy
另一種常用的特征選擇方法就是直接度量每個(gè)特征對(duì)模型精確率的影響。主要思路是打亂每個(gè)特征的特征值順序，并且度量順序變動(dòng)對(duì)模型的精確率的影響。很明顯，對(duì)于不重要的變量來說，打亂順序?qū)δＰ偷木_率影響不會(huì)太大，但是對(duì)于重要的變量來說，打亂順序就會(huì)降低模型的精確率。

5 兩種頂層特征選擇算法
之所以叫做頂層，是因?yàn)樗麄兌际墙⒃诨谀Ｐ偷奶卣鬟x擇方法基礎(chǔ)之上的，例如回歸和SVM，在不同的子集上建立模型，然后匯總最終確定特征得分。

5.1 穩(wěn)定性選擇 Stability selection
穩(wěn)定性選擇是一種基于二次抽樣和選擇算法相結(jié)合較新的方法，選擇算法可以是回歸、SVM或其他類似的方法。它的主要思想是在不同的數(shù)據(jù)子集和特征子集上運(yùn)行特征選擇算法，不斷的重復(fù)，最終匯總特征選擇結(jié)果，比如可以統(tǒng)計(jì)某個(gè)特征被認(rèn)為是重要特征的頻率（被選為重要特征的次數(shù)除以它所在的子集被測試的次數(shù)）。理想情況下，重要特征的得分會(huì)接近100%。稍微弱一點(diǎn)的特征得分會(huì)是非0的數(shù)，而最無用的特征得分將會(huì)接近于0。

5.2 遞歸特征消除 Recursive feature elimination (RFE)
遞歸特征消除的主要思想是反復(fù)的構(gòu)建模型（如SVM或者回歸模型）然后選出最好的（或者最差的）的特征（可以根據(jù)系數(shù)來選），把選出來的特征放到一遍，然后在剩余的特征上重復(fù)這個(gè)過程，直到所有特征都遍歷了。這個(gè)過程中特征被消除的次序就是特征的排序。因此，這是一種尋找最優(yōu)特征子集的貪心算法。

RFE的穩(wěn)定性很大程度上取決于在迭代的時(shí)候底層用哪種模型。例如，假如RFE采用的普通的回歸，沒有經(jīng)過正則化的回歸是不穩(wěn)定的，那么RFE就是不穩(wěn)定的；假如采用的是Ridge，而用Ridge正則化的回歸是穩(wěn)定的，那么RFE就是穩(wěn)定的。
7、特征獲取方法的選取原則
a、處理的數(shù)據(jù)類型
b、處理的問題規(guī)模
c、問題需要分類的數(shù)量
d、對(duì)噪聲的容忍能力
e、無噪聲環(huán)境下，產(chǎn)生穩(wěn)定性好、最優(yōu)特征子集的能力。

互信息Mutual Informantion

?yj對(duì)xi的互信息定義為后驗(yàn)概率與先驗(yàn)概率比值的對(duì)數(shù)。

互信息越大，表明yj對(duì)于確定xi的取值的貢獻(xiàn)度越大。

實(shí)際上，互信息衡量的是xi與y的獨(dú)立性，如果他倆獨(dú)立，則互信息發(fā)值為零，則xi與y不相關(guān)，則可以剔除xi，反之，如果互信息發(fā)值越大則他們的相關(guān)性越大

基于期望交叉熵的特征項(xiàng)選擇

1初始化特征集F為空

2掃描i從1到n，

　　如果第i個(gè)特征不再F中，那么將特征i和F放到一起Fi在只使用Fi中特征的情況下，利用交叉驗(yàn)證來得到Fi的錯(cuò)誤率。

3從上步中得到的n個(gè)Fi中選擇出錯(cuò)誤率最小的Fi，更新F為Fi

　　如果F中的特征數(shù)達(dá)到n或者預(yù)設(shè)定的閾值（如果有），那么輸出整個(gè)搜索過程中最好的F，沒達(dá)到轉(zhuǎn)到2

????