Abstract: This article discusses the requirements for portable electronic devices with cryptographic capabilities to perform very secure network authentication, fare collection, vending system regulation, etc. It also shows how the DS1963S or DS1961S iButtons? meet these requirements, such as secret protection, "Zero Knowledge Proof", and secure challenge-response through the secure hash algorithm (SHA-1).
Increasingly, the world is turning to portable electronic devices with cryptographic capabilities to perform very secure network authentication, virtual private networking, vending system regulation, fare collection, and employee or citizen identification. The design of such a portable device (or token) requires careful study of the methods by which cryptographers authenticate and protect sensitive data and monetary information. Of course, an e-cash or identification token must be portable, durable, and secure, but it quickly becomes obvious that there are several additional cryptographic, electrical, and physical requirements that a secure token must satisfy.
The most critical function for a truly secure token is that of authentication. A token must be able to prove that it is authorized by the issuer (the service provider), and that it is authentic. A token can prove that it is authorized simply by virtue of the fact that it contains encrypted information that only the issuing authority could have created. Secure authentication, however, is a far more difficult issue. The device must be able to prove that it is not a fake or duplicate, and this requires some very special hardware functionality. A device will not be trusted if its design cannot be freely examined, so secrets in design or function are all but impossible to keep. If we assume that the inner workings of the device are published and widely known, then we must also assume that anyone with sufficient skill could build an emulation of the device and bypass some of the special controls that the device hardware imposes. Any token design based on security by obscurity is doomed to failure.
In cryptographic circles, truly secure authentication is handled by a method called challenge-and-response. This method involves a secret that is known only to valid tokens and hosts, and methods whereby tokens can prove that they know the secret, which proves that they are authentic. Of course, the secret must never be revealed in the process, and that is where a cryptographic concept called Zero Knowledge Proof comes into play. The token must support a mechanism where it can prove that it knows a secret without revealing any information about it. At first glance, this may seem impossible, but it is a common exercise in secure cryptographic systems. Here is how the scheme works:
When a suspect token arrives, the host system creates a very big number, called a challenge, entirely at random, and sends it to the token. The token takes this challenge and, together with an internally stored secret, performs a complex mathematical operation on it. Then, it returns the result of the operation to the host (see Figure 1). The host, also knowing the same secret, performs the same special mathematical operation internally, and then compares the results. If the response from the token matches the one computed in the host, then the token has proven that it knows the secret, without revealing it (the essence of a Zero Knowledge Proof). Eavesdropping on this conversation is of no use to an attacker who does not know the secret. This is because the challenge is different each time; it is randomly generated. The next challenge can never be predicted. The secret remains safely hidden inside the token, and the host knows that the token is authentic (because only authentic tokens know the secret).
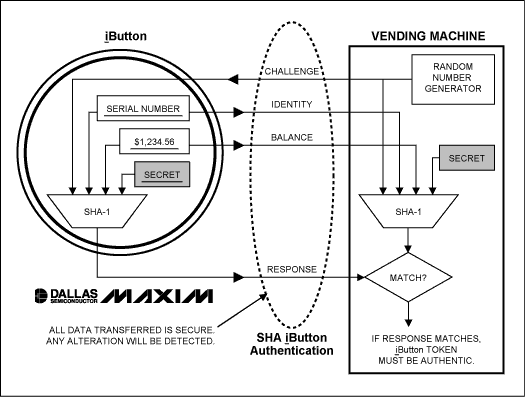
Figure 1. SHA iButton authentication.
Of course, it is critical that the complex mathematical algorithm used is not reversible, since the attacker could run the operation in reverse and derive the secret. In fact, the choice of algorithm may be the single most important factor in judging the security of a challenge and response scheme. Electronic tokens have been created in the past that use home-brewed algorithms, stream-ciphers, rolling-codes, or cryptographic algorithms that have been curtailed or reduced for this purpose, but they have not been widely accepted. The problem is that without extensive peer-review, there is no assurance that these algorithms are secure against attack. And there is no guarantee that these algorithms have no "back doors" (intentional or accidental) that may be known only to the device manufacturer.
To make a truly secure cryptographic token, the algorithm selected must be one that is well-known, trusted, time-tested, and widely peer-reviewed in the global cryptographic community. An algorithm that takes input data and irreversibly creates a digest of that data is called a one-way hash function. One of the most studied and trusted one-way hash functions is SHA-1 (Secure Hash Algorithm). This government-approved (FIPS 180-1) algorithm is the basis of modern digital signatures and document protection schemes. It has a long history in the cryptographic community, is peer-reviewed, and is widely trusted.
However, SHA-1 is a complex algorithm that involves multiple 32-bit 5-way adds, complex logical functions, data shifting, and a great deal of repetition. Implementations of the SHA-1 algorithm in silicon have generally required large die areas and so made fairly expensive tokens. A new method has been devised to perform the algorithm in a serialized fashion, reducing the die area by a factor of 10 or more and making a reasonably priced SHA-1-based token possible.
Another critical feature of a truly secure token is a globally unique and unalterable identity. Including the unique token serial number as an additional input to the authentication algorithm binds the physical token and the contents together, making duplication of monetary value or credentials among tokens impossible.
When a secure token is used in monetary applications, the data it contains (presumably the account balance) is said to be dynamic, because the critical value is read, debited, and rewritten each time the device is used. This type of usage model introduces a type of attack known by cryptographers as a replay attack. That is to say, an attacker can record the value data from the token, and then deplete the token making legitimate purchases. He can then restore (or replay) the original data, and thereby restore the monetary value of the token to be spent repeatedly. This replay can be prevented only if the token provides mechanisms that make each instance of the data that it contains unique. The truly secure monetary token therefore provides a special counter. This counter is incremented each time the device is written to and cannot be wrapped-around, reset, decremented, or reloaded. Then, by including this counter value in the input to the authentication algorithm, the monetary data, the device identity, and the monetary instance are all bound together. Should the data be taken from the device and written back later, it will be found invalid because the counter will have changed. It's the same value, but it is not the same instance of the value.
An interesting feature of the challenge-and-response authentication process is that the data is also protected while en route from the token to the host. Since the data, the token identity, and the instance counter are all included in the SHA-1 algorithm input, any attempt to alter or inject data bits into the communications path between the token and the host will also render the transaction invalid. This means that any number of untrusted intermediaries can handle this challenge-and-response data exchange and the process remains secure. A distant server on the Internet can authenticate a user's token at a home computer through a myriad of routers, bridges, hubs, and eavesdroppers, and security is not compromised in the slightest bit.
Another important requirement for a secure authentication token is that it is able to protect the secrets that it holds. Plastic cards with embedded silicon chips are difficult to protect against physical attacks, and typical memory devices have no special provisions for secure storage areas where secrets might be kept. A secure token must provide a high level of physical security to protect the secrets it contains.
Cryptography also provides methods whereby the secret in each device may be derived from another master secret, which is not stored in the device, in combination with the unique device identity. This provides a unique secret for each device and prevents a system-wide break (called a class break) should the secret in any one device be compromised. Monetary systems, generally, also use one secret (stored inside the token) for token authentication, and another secret (not stored in the token) for validation of the monetary values stored in the token. This limits the scope of a physical attack on a token to just the ability to emulate that one, and only that one, token. This severely limits the profitability of a physical attack.
An often overlooked avenue of attack occurs at the service provider's facilities where an unscrupulous employee gains access to the critical secrets by which the scheme assures authenticity. To overcome this problem, cryptographers offer a method called Secret Sharing. The actual secret does not actually exist, but instead is the result of computations that combine two or more partial secrets. The service provider maintains these partial secrets on separate systems, at separate locations, and allows no one to have access to more than one of them. Without all of the partial secrets applied in the proper sequence, the actual secret cannot be computed. A truly effective, secure token must provide a means to combine the partial secrets entirely inside the token so that the final secret never actually exists where any human can ever observe it. As the token moves through the service provider's initialization process, it is injected with each subsequent partial secret, and the actual secret is being computed entirely inside each device. As a final step, the unique device identity is also injected into the process, so the resulting device secret is unique to it, and the master secret never actually exists where it could be compromised.
A secure electronic token that can be strongly authenticated also makes for a very secure key for door locks, access control systems, and equipment control lockouts. An electronic key using challenge and response cannot be duplicated or altered; and eavesdropping attacks are useless. In this application, the data is said to be static because, unlike an e-cash application, it does not change with each use. The ability to have the token authenticate the person who presents it, adds even more to the security of the system; even in systems that have no provisions for such PIN or password protection.
Peer-to-peer authentication applications allow networked appliances to authenticate one another. This protects them from being operated by outsiders. Tokens that perform the authentication quickly, and that protect the secrets inside the token, greatly reduce the physical security required around the appliance. The token can also be used to quickly generate unique session keys for the encryption of control commands or sensitive data.
The Dallas Semiconductor DS1963S iButton is a secure, electronic token that satisfies all of these requirements. Each token has a globally unique, factory-lasered 64-bit identity, 512 bytes of lithium-backed NV RAM data storage area, and eight protected 64-bit secrets. All of this is housed in a small, rugged stainless-steel container. Two-way communication with the device is performed on a single data conductor at up to 140kbps, and SHA-1 is performed internally in under 500 microseconds. The 64-bit secret size would require about 9,223,000,000,000,000,000 attempts to break by brute-force methods, making a brute-force attack unrealistic. The iButton can be worn like jewelry, attached to an ID card or badge, or carried like a key. It can be attached to a container or bin, to a product or shipping carton. It can also be embedded in a component or circuit board.
The Dallas Semiconductor DS1961S iButton is an EEPROM version of the DS1963S. It has 128 bytes of memory and provides a write-protection scheme where the host system must satisfy a SHA authentication before the device can be altered.
The DS1963S also has the ability to serve as a coprocessor in vending and toll systems where the processing power and speed at the host side is usually limited. Used as a co-processor, the DS1963S can safely store and protect the system secrets, perform the SHA-1 algorithm very quickly, and store the collected funds safely, as well as providing a globally unique serial number that identifies the fare box or vending machine. As a co-processor, the DS1963S iButton can also hold critical configuration and pricing data used by the host. The host electronics are reduced to simply moving data between iButtons. E-cash systems have been demonstrated that use all of the security features described herein and perform entire monetary transactions in under 50 milliseconds.
The DS1961S, which is also available in chip form, can also be simply embedded in networked devices (using only a single port pin for communication). This provides strong cryptographic authentication between networked devices, opening up new possibilities for interrogating and controlling them using the Internet. Networked devices can quickly and reliably authenticate one another and generate random number-based session keys for data encryption, all in a single exchange of messages. The system secrets are safely stored in protected EEPROM, and there is almost no overhead incurred to add strong cryptographic security to networked devices.
Increasingly, the world is turning to portable electronic devices with cryptographic capabilities to perform very secure network authentication, virtual private networking, vending system regulation, fare collection, and employee or citizen identification. The design of such a portable device (or token) requires careful study of the methods by which cryptographers authenticate and protect sensitive data and monetary information. Of course, an e-cash or identification token must be portable, durable, and secure, but it quickly becomes obvious that there are several additional cryptographic, electrical, and physical requirements that a secure token must satisfy.
The most critical function for a truly secure token is that of authentication. A token must be able to prove that it is authorized by the issuer (the service provider), and that it is authentic. A token can prove that it is authorized simply by virtue of the fact that it contains encrypted information that only the issuing authority could have created. Secure authentication, however, is a far more difficult issue. The device must be able to prove that it is not a fake or duplicate, and this requires some very special hardware functionality. A device will not be trusted if its design cannot be freely examined, so secrets in design or function are all but impossible to keep. If we assume that the inner workings of the device are published and widely known, then we must also assume that anyone with sufficient skill could build an emulation of the device and bypass some of the special controls that the device hardware imposes. Any token design based on security by obscurity is doomed to failure.
In cryptographic circles, truly secure authentication is handled by a method called challenge-and-response. This method involves a secret that is known only to valid tokens and hosts, and methods whereby tokens can prove that they know the secret, which proves that they are authentic. Of course, the secret must never be revealed in the process, and that is where a cryptographic concept called Zero Knowledge Proof comes into play. The token must support a mechanism where it can prove that it knows a secret without revealing any information about it. At first glance, this may seem impossible, but it is a common exercise in secure cryptographic systems. Here is how the scheme works:
When a suspect token arrives, the host system creates a very big number, called a challenge, entirely at random, and sends it to the token. The token takes this challenge and, together with an internally stored secret, performs a complex mathematical operation on it. Then, it returns the result of the operation to the host (see Figure 1). The host, also knowing the same secret, performs the same special mathematical operation internally, and then compares the results. If the response from the token matches the one computed in the host, then the token has proven that it knows the secret, without revealing it (the essence of a Zero Knowledge Proof). Eavesdropping on this conversation is of no use to an attacker who does not know the secret. This is because the challenge is different each time; it is randomly generated. The next challenge can never be predicted. The secret remains safely hidden inside the token, and the host knows that the token is authentic (because only authentic tokens know the secret).

Figure 1. SHA iButton authentication.
Of course, it is critical that the complex mathematical algorithm used is not reversible, since the attacker could run the operation in reverse and derive the secret. In fact, the choice of algorithm may be the single most important factor in judging the security of a challenge and response scheme. Electronic tokens have been created in the past that use home-brewed algorithms, stream-ciphers, rolling-codes, or cryptographic algorithms that have been curtailed or reduced for this purpose, but they have not been widely accepted. The problem is that without extensive peer-review, there is no assurance that these algorithms are secure against attack. And there is no guarantee that these algorithms have no "back doors" (intentional or accidental) that may be known only to the device manufacturer.
To make a truly secure cryptographic token, the algorithm selected must be one that is well-known, trusted, time-tested, and widely peer-reviewed in the global cryptographic community. An algorithm that takes input data and irreversibly creates a digest of that data is called a one-way hash function. One of the most studied and trusted one-way hash functions is SHA-1 (Secure Hash Algorithm). This government-approved (FIPS 180-1) algorithm is the basis of modern digital signatures and document protection schemes. It has a long history in the cryptographic community, is peer-reviewed, and is widely trusted.
However, SHA-1 is a complex algorithm that involves multiple 32-bit 5-way adds, complex logical functions, data shifting, and a great deal of repetition. Implementations of the SHA-1 algorithm in silicon have generally required large die areas and so made fairly expensive tokens. A new method has been devised to perform the algorithm in a serialized fashion, reducing the die area by a factor of 10 or more and making a reasonably priced SHA-1-based token possible.
Another critical feature of a truly secure token is a globally unique and unalterable identity. Including the unique token serial number as an additional input to the authentication algorithm binds the physical token and the contents together, making duplication of monetary value or credentials among tokens impossible.
When a secure token is used in monetary applications, the data it contains (presumably the account balance) is said to be dynamic, because the critical value is read, debited, and rewritten each time the device is used. This type of usage model introduces a type of attack known by cryptographers as a replay attack. That is to say, an attacker can record the value data from the token, and then deplete the token making legitimate purchases. He can then restore (or replay) the original data, and thereby restore the monetary value of the token to be spent repeatedly. This replay can be prevented only if the token provides mechanisms that make each instance of the data that it contains unique. The truly secure monetary token therefore provides a special counter. This counter is incremented each time the device is written to and cannot be wrapped-around, reset, decremented, or reloaded. Then, by including this counter value in the input to the authentication algorithm, the monetary data, the device identity, and the monetary instance are all bound together. Should the data be taken from the device and written back later, it will be found invalid because the counter will have changed. It's the same value, but it is not the same instance of the value.
An interesting feature of the challenge-and-response authentication process is that the data is also protected while en route from the token to the host. Since the data, the token identity, and the instance counter are all included in the SHA-1 algorithm input, any attempt to alter or inject data bits into the communications path between the token and the host will also render the transaction invalid. This means that any number of untrusted intermediaries can handle this challenge-and-response data exchange and the process remains secure. A distant server on the Internet can authenticate a user's token at a home computer through a myriad of routers, bridges, hubs, and eavesdroppers, and security is not compromised in the slightest bit.
Another important requirement for a secure authentication token is that it is able to protect the secrets that it holds. Plastic cards with embedded silicon chips are difficult to protect against physical attacks, and typical memory devices have no special provisions for secure storage areas where secrets might be kept. A secure token must provide a high level of physical security to protect the secrets it contains.
Cryptography also provides methods whereby the secret in each device may be derived from another master secret, which is not stored in the device, in combination with the unique device identity. This provides a unique secret for each device and prevents a system-wide break (called a class break) should the secret in any one device be compromised. Monetary systems, generally, also use one secret (stored inside the token) for token authentication, and another secret (not stored in the token) for validation of the monetary values stored in the token. This limits the scope of a physical attack on a token to just the ability to emulate that one, and only that one, token. This severely limits the profitability of a physical attack.
An often overlooked avenue of attack occurs at the service provider's facilities where an unscrupulous employee gains access to the critical secrets by which the scheme assures authenticity. To overcome this problem, cryptographers offer a method called Secret Sharing. The actual secret does not actually exist, but instead is the result of computations that combine two or more partial secrets. The service provider maintains these partial secrets on separate systems, at separate locations, and allows no one to have access to more than one of them. Without all of the partial secrets applied in the proper sequence, the actual secret cannot be computed. A truly effective, secure token must provide a means to combine the partial secrets entirely inside the token so that the final secret never actually exists where any human can ever observe it. As the token moves through the service provider's initialization process, it is injected with each subsequent partial secret, and the actual secret is being computed entirely inside each device. As a final step, the unique device identity is also injected into the process, so the resulting device secret is unique to it, and the master secret never actually exists where it could be compromised.
A secure electronic token that can be strongly authenticated also makes for a very secure key for door locks, access control systems, and equipment control lockouts. An electronic key using challenge and response cannot be duplicated or altered; and eavesdropping attacks are useless. In this application, the data is said to be static because, unlike an e-cash application, it does not change with each use. The ability to have the token authenticate the person who presents it, adds even more to the security of the system; even in systems that have no provisions for such PIN or password protection.
Peer-to-peer authentication applications allow networked appliances to authenticate one another. This protects them from being operated by outsiders. Tokens that perform the authentication quickly, and that protect the secrets inside the token, greatly reduce the physical security required around the appliance. The token can also be used to quickly generate unique session keys for the encryption of control commands or sensitive data.
The Dallas Semiconductor DS1963S iButton is a secure, electronic token that satisfies all of these requirements. Each token has a globally unique, factory-lasered 64-bit identity, 512 bytes of lithium-backed NV RAM data storage area, and eight protected 64-bit secrets. All of this is housed in a small, rugged stainless-steel container. Two-way communication with the device is performed on a single data conductor at up to 140kbps, and SHA-1 is performed internally in under 500 microseconds. The 64-bit secret size would require about 9,223,000,000,000,000,000 attempts to break by brute-force methods, making a brute-force attack unrealistic. The iButton can be worn like jewelry, attached to an ID card or badge, or carried like a key. It can be attached to a container or bin, to a product or shipping carton. It can also be embedded in a component or circuit board.
The Dallas Semiconductor DS1961S iButton is an EEPROM version of the DS1963S. It has 128 bytes of memory and provides a write-protection scheme where the host system must satisfy a SHA authentication before the device can be altered.
The DS1963S also has the ability to serve as a coprocessor in vending and toll systems where the processing power and speed at the host side is usually limited. Used as a co-processor, the DS1963S can safely store and protect the system secrets, perform the SHA-1 algorithm very quickly, and store the collected funds safely, as well as providing a globally unique serial number that identifies the fare box or vending machine. As a co-processor, the DS1963S iButton can also hold critical configuration and pricing data used by the host. The host electronics are reduced to simply moving data between iButtons. E-cash systems have been demonstrated that use all of the security features described herein and perform entire monetary transactions in under 50 milliseconds.
The DS1961S, which is also available in chip form, can also be simply embedded in networked devices (using only a single port pin for communication). This provides strong cryptographic authentication between networked devices, opening up new possibilities for interrogating and controlling them using the Internet. Networked devices can quickly and reliably authenticate one another and generate random number-based session keys for data encryption, all in a single exchange of messages. The system secrets are safely stored in protected EEPROM, and there is almost no overhead incurred to add strong cryptographic security to networked devices.
 電子發燒友App
電子發燒友App

























評論