于一個開發人員,可能聽說過 FPGA,甚至在大學課程設計中,可能拿 FPGA 做過計算機體系架構相關的驗證,但是對于它的第一印象可能覺得這是硬件工程師干的事兒。
目前,隨著人工智能的興起,GPU 借助深度學習,走上了歷史的舞臺,并且正如火如荼的跑著各種各樣的業務,從 training 到 inference 都有它的身影。FPGA 也借著這股浪潮,慢慢地走向數據中心,發揮著它的優勢。所以接下來就講講 FPGA 如何能讓程序員們更好友好的開發,而不需要寫那些煩人的 RTL 代碼,不需要使用 VCS,Modelsim 這樣的仿真軟件,就能輕輕松松實現 unit test。
實現這一編程思想的轉變,是因為 FPGA 借助 OpenCL 實現了編程,程序員只需要通過 C/C++ 添加適當的 pragma 就能實現 FPGA 編程。為了讓您用 OpenCL 實現的 FPGA 應用能夠有更高的性能,您需要熟悉如下介紹的硬件。另外,將會介紹編譯優化選項,有助于將您的 OpenCL 應用更好的實現 RTL 的轉換和映射,并部署到 FPGA 上執行。
FPGA 概覽
FPGA 是高規格的集成電路,可以實現通過不斷的配置和拼接,達到無限精度的函數功能,因為它不像 CPU 或者 GPU 那樣,基本數據類型的位寬都是固定的,相反 FPGA 能夠做的非常靈活。在使用 FPGA 的過程中,特別適合一些 low-level 的操作,比如像 bit masking、shifting、addition 這樣的操作都可以非常容易的實現。
為了達到并行化計算,FPGA 內部包含了查找表(LUTs),寄存器(register),片上存儲(on-chip memory)以及算術運算硬核(比如數字信號處理器 (DSP) 塊)。這些 FPGA 內部的模塊通過網絡連接在一起,通過編程的手段,可以對連接進行配置,從而實現特定的邏輯功能。這種網絡連接可重配的特性為 FPGA 提供了高層次可編程的能力。(FPGA 的可編程性就體現在改變各個模塊和邏輯資源之間的連接方式)
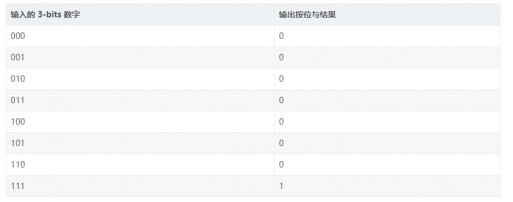
舉個例子,查找表(LUTs)體現的 FPGA 可編程能力,對于程序猿來說,可以等價理解為一個存儲器(RAM)。對于 3-bits 輸入的 LUT 可以等價理解為一個擁有 3 位地址線并且 8 個 1-bit 存儲單元的存儲器(一個 8 長度的數組,數組內每個元素是 1bit)。那么當需要實現 3-bits 數字按位與操作的時候,8 長度數組存的是 3-bits 輸入數字的按位與結果,一共是 8 種可能性。當需要實現 3-bits 按位異或的時候,8 長度數組存的是 3-bits 輸入數字的按位異或結果,一共也是 8 種可能性。這樣,在一個時鐘周期內,3-bits 的按位運算就能夠獲取到,并且實現不同功能的按位運算,完全是可編程的(等價于修改 RAM 內的數值)。
3-bits 輸入 LUT 實現按位與(bit-wise AND):
注:3-bits 輸入 LUT 查找表
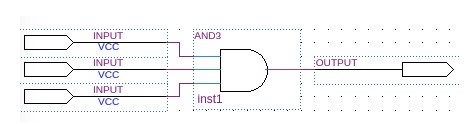
我們看到的三輸入的按位與操作,如下所示,在 FPGA 內部,可通過 LUT 實現。
如上展示了 3 輸入,1 輸出的 LUT 實現。當將 LUT 并聯,串聯等方式結合起來后就可以實現更加復雜的邏輯運算了。
傳統 FPGA 開發
▍傳統 FPGA 與軟件開發對比
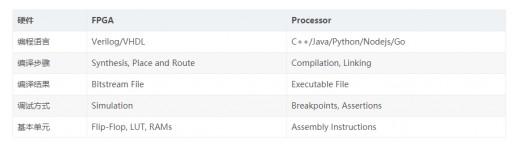
對于傳統的 FPGA 開發與軟件開發,工具鏈可以通過下表簡單對比:
注:傳統 FPGA 與軟件開發對比表
重點介紹一下,編譯階段的 Synthesis (綜合),這部分與軟件開發的編譯有較大的不同。一般的處理器 CPU、GPU 等,都是已經生產出來的 ASIC,有各自的指令集可以使用。但是對于 FPGA,一切都是空白,有的只是零部件,什么都沒有,但是可以自己創造任何結構形式的電路,自由度非常的高。這種自由度是 FPGA 的優勢,也是開發過程中的劣勢。
寫到這里,讓我想起了最近 《神秘的程序員們》中的一個梗:
傳統的 FPGA 開發就像 10 歲時候的 Linux,想吃一個蛋糕,需要自己從原材料開始加工。FPGA 正是這種狀態,想要實現一個算法,需要寫 RTL,需要設計狀態機,需要仿真正確性。
▍傳統 FPGA 開發方式
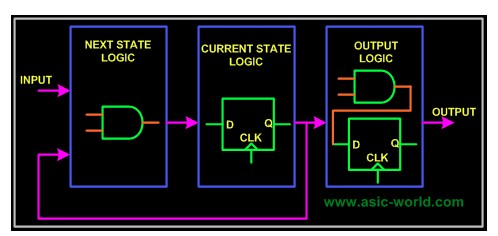
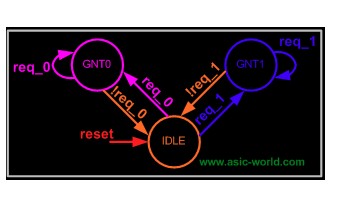
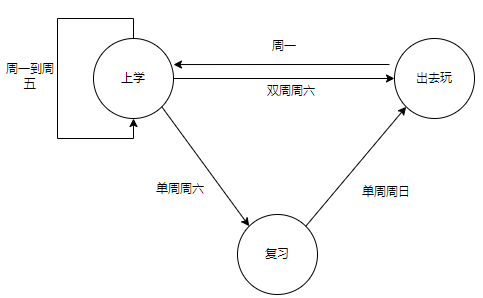
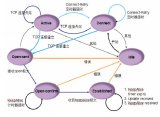
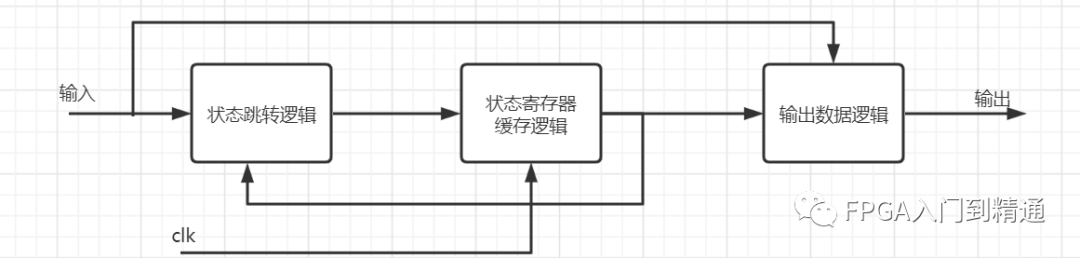
復雜系統,需要使用有限狀態機(FSM),一般就需要設計下圖包含的三部分邏輯:組合電路,時序電路,輸出邏輯。通過組合邏輯獲取下一個狀態是什么,時序邏輯用于存儲當前狀態,輸出邏輯混合組合、時序電路,得到最終輸出結果。
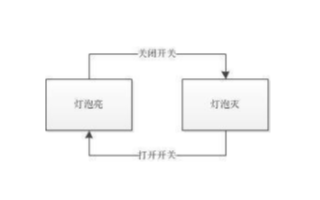
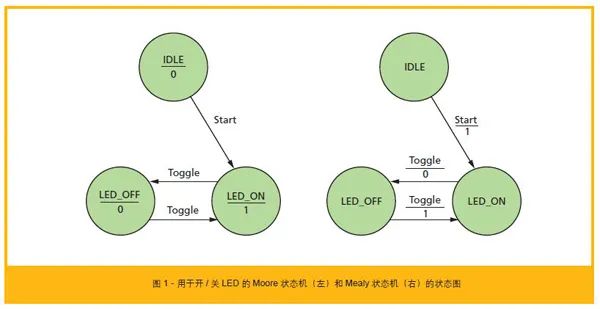
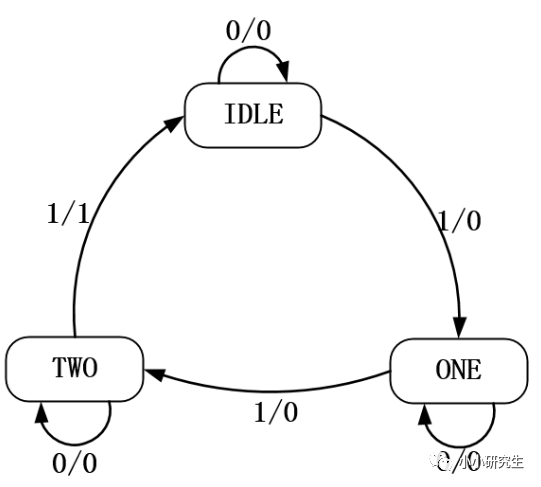
然后,針對具體算法,設計邏輯在狀態機中的流轉過程:
實現的 RTL 是這樣的:
module fsm_using_single_always (
clock , // clockreset , // Active high, syn resetreq_0 , // Request 0req_1 , // Request 1gnt_0 , // Grant 0gnt_1
);//=============Input Ports=============================input clock,reset,req_0,req_1; //=============Output Ports===========================output gnt_0,gnt_1;//=============Input ports Data Type===================wire clock,reset,req_0,req_1;//=============Output Ports Data Type==================reg gnt_0,gnt_1;//=============Internal Constants======================parameter SIZE = 3 ;
parameter IDLE = 3‘b001,GNT0 = 3’b010,GNT1 = 3‘b100 ;//=============Internal Variables======================reg [SIZE-1:0] state ;// Seq part of the FSMreg [SIZE-1:0] next_state ;// combo part of FSM//==========Code startes Here==========================always @ (posedge clock)begin : FSMif (reset == 1’b1) begin
state 《= #1 IDLE;
gnt_0 《= 0;
gnt_1 《= 0;end else
case(state)
IDLE : if (req_0 == 1‘b1) begin
state 《= #1 GNT0;
gnt_0 《= 1; end else if (req_1 == 1’b1) begin
gnt_1 《= 1;
state 《= #1 GNT1; end else begin
state 《= #1 IDLE; end
GNT0 : if (req_0 == 1‘b1) begin
state 《= #1 GNT0; end else begin
gnt_0 《= 0;
state 《= #1 IDLE; end
GNT1 : if (req_1 == 1’b1) begin
state 《= #1 GNT1; end else begin
gnt_1 《= 0;
state 《= #1 IDLE; end
default : state 《= #1 IDLE;
endcaseendendmodule // End of Module arbiter
傳統的 RTL 設計,對于程序員簡直就是噩夢啊,夢啊,啊~~~工具鏈完全不同,開發思路完全不同,還要分析時序,一個 Clock 節拍不對,就要推翻重來,重新驗證,一切都顯得太底層,不是很方便。那么,這些就交給專業的 FPGAer 吧,下面介紹的 OpenCL 開發 FPGA,有點像 25 歲的 Linux 了。有了高層次的抽象。用起來自然也會更加方便。
▍基于 OpenCL 的 FPGA 開發
OpenCL 對于 FPGA 開發,注入了新鮮的血液,一種面向異構系統的編程語言,將 FPGA 最為異構實現的一種可選設備。由 CPU Host 端控制整個程序的執行流程,FPGA Device 端則作為異構加速的一種方式。異構架構,有助于解放 CPU,將 CPU 不擅長的處理方式,下發到 Device 端處理。目前典型的異構 Device 有:GPU、Intel Phi、FPGA。
OpenCL 是一個用于異構平臺編程的框架,主要的異構設備有 CPU、GPU、DSP、FPGA 以及一些其它的硬件加速器。OpenCL 基于 C99 來開發設備端代碼,并且提供了相應的 API 可以調用。OpenCL 提供了標準的并行計算的接口,以支持任務并行和數據并行的計算方式。
OpenCL 案例分析
這里采用 Altera 官網的矩陣乘法案例進行分析。可以通過如下鏈接下載案例:Altera OpenCL Matrix Multiplication
代碼結構如下:
。|-- common| |-- inc| | `-- AOCLUtils| | |-- aocl_utils.h| | |-- opencl.h| | |-- options.h| | `-- scoped_ptrs.h| |-- readme.css| `-- src| `-- AOCLUtils| |-- opencl.cpp| `-- options.cpp`-- matrix_mult
|-- Makefile
|-- README.html
|-- device
| `-- matrix_mult.cl
`-- host
|-- inc
| `-- matrixMult.h
`-- src
`-- main.cpp
其中,和 FPGA 相關的代碼是 matrix_mult.cl ,該部分代碼描述了 kernel 函數,這部分函數會通過編譯器生成 RTL 代碼,然后 map 到 FPGA 電路中。
kernel 函數的定義如下:
__kernel
__attribute((reqd_work_group_size(BLOCK_SIZE,BLOCK_SIZE,1)))
__attribute((num_simd_work_items(SIMD_WORK_ITEMS)))void matrixMult( __global float *restrict C,
__global float *A,
__global float *B,
int A_width,
int B_width)
模式比較固定,需要注意的是 __global 指明從 CPU 傳過來的數據,存放到全局內存中,可以是 FPGA 片上存儲資源,DDR,QDR 等,這個視 FPGA 的 OpenCL BSP 驅動,會有所區別。num_simd_work_items 用于指明 SIMD 的寬度。reqd_work_group_size 指明了工作組的大小。這些概念,可以參考 OpenCL 的使用手冊。
函數實現如下:
// 聲明本地存儲,暫存數組的某一個 BLOCK__local float A_local[BLOCK_SIZE][BLOCK_SIZE];
__local float B_local[BLOCK_SIZE][BLOCK_SIZE];// Block indexint block_x = get_group_id(0);int block_y = get_group_id(1);// Local ID index (offset within a block)int local_x = get_local_id(0);int local_y = get_local_id(1);// Compute loop boundsint a_start = A_width * BLOCK_SIZE * block_y;int a_end = a_start + A_width - 1;int b_start = BLOCK_SIZE * block_x;float running_sum = 0.0f;for (int a = a_start, b = b_start; a 《= a_end; a += BLOCK_SIZE, b += (BLOCK_SIZE * B_width))
{ // 從 global memory 讀取相應 BLOCK 數據到 local memory
A_local[local_y][local_x] = A[a + A_width * local_y + local_x];
B_local[local_x][local_y] = B[b + B_width * local_y + local_x]; // Wait for the entire block to be loaded.
barrier(CLK_LOCAL_MEM_FENCE); // 計算部分,將計算單元并行展開,形成乘法加法樹
#pragma unroll
for (int k = 0; k 《 BLOCK_SIZE; ++k)
{
running_sum += A_local[local_y][k] * B_local[local_x][k];
} // Wait for the block to be fully consumed before loading the next block.
barrier(CLK_LOCAL_MEM_FENCE);
}// Store result in matrix CC[get_global_id(1) * get_global_size(0) + get_global_id(0)] = running_sum;
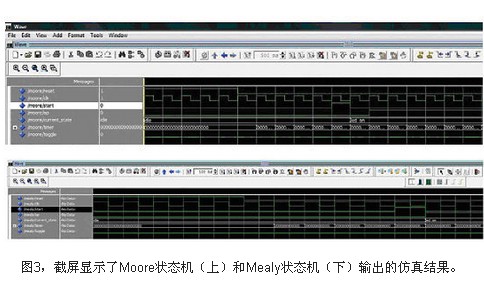
采用 CPU 模擬仿真 FPGA
對其進行仿真,不需要 programer 關心具體的時序是怎么走的,只需要驗證邏輯功能就可以,Altera OpenCL SDK 提供了 CPU 仿真 Device 設備的功能,采用如下方式進行:
# To generate a .aocx file for debugging that targets a specific accelerator board$ aoc -march=emulator device/matrix_mult.cl -o bin/matrix_mult.aocx --fp-relaxed --fpc --no-interleaving default --board 《your-board》# Generate Host exe.$ make# To run the application$ env CL_CONTEXT_EMULATOR_DEVICE_ALTERA=8 。/bin/host -ah=512 -aw=512 -bw=512
上述腳本中,通過 -march=emulator 設置創建一個可用于 CPU debug 的設備可執行文件。-g 添加調試 flag。—board 用于創建適配該設備的 debugging 文件。CL_CONTEXT_EMULATOR_DEVICE_ALTERA 為用于 CPU 仿真的設備數量。
當執行上述腳本后,輸出如下:
$ env CL_CONTEXT_EMULATOR_DEVICE_ALTERA=8 。/bin/host -ah=512 -aw=512 -bw=512Matrix sizes:
A: 512 x 512
B: 512 x 512
C: 512 x 512Initializing OpenCL
Platform: Altera SDK for OpenCL
Using 8 device(s)
EmulatorDevice : Emulated Device
。..
EmulatorDevice : Emulated Device
Using AOCX: matrix_mult.aocx
Generating input matrices
Launching for device 0 (global size: 512, 64)
。..
Launching for device 7 (global size: 512, 64)
Time: 5596.620 ms
Kernel time (device 0): 5500.896 ms
。..
Kernel time (device 7): 5137.931 ms
Throughput: 0.05 GFLOPS
Computing reference output
Verifying
Verification: PASS
通過仿真時候設置 Device = 8,模擬 8 個設備運行 (512, 512) * (512, 512) 規模的矩陣,最終驗證正確。接下來就可以將其真正編譯到 FPGA 設備上后運行。
FPGA 設備上運行矩陣乘
這個時候,真正要將代碼下載到 FPGA 上執行了,這時候,只需要做一件事,那就是用 OpenCL SDK 提供的編譯器,將 *.cl 代碼適配到 FPGA 上,執行編譯命令如下:
$ aoc device/matrix_mult.cl -o bin/matrix_mult.aocx --fp-relaxed --fpc --no-interleaving default --board 《your-board》
這個過程比較慢,一般需要幾個小時到 10 幾個小時,視 FPGA 上資源大小而定。(目前這部分時間太長暫時無法解決,因為這里的編譯,其實是在行程一個能夠正常工作的電路,軟件會進行布局布線等工作)
等待編譯完成后,將生成的 matrix_mult.aocx 文件燒寫到 FPGA 上就 ok 啦。
燒寫的命令如下:
$ aocl program 《your-board》 matrix_mult.aocx
這時候,大功告成,可以運行 host 端程序了:
$ 。/host -ah=512 -aw=512 -bw=512Matrix sizes:
A: 512 x 512
B: 512 x 512
C: 512 x 512Initializing OpenCL
Platform: Altera SDK for OpenCL
Using 1 device(s)
《your-board》 : Altera OpenCL QPI FPGA
Using AOCX: matrix_mult.aocx
Generating input matrices
Launching for device 0 (global size: 512, 512)
Time: 2.253 ms
Kernel time (device 0): 2.191 ms
Throughput: 119.13 GFLOPS
Computing reference output
Verifying
Verification: PASS
可以看到,矩陣乘法能夠在 FPGA 上正常運行,吞吐大概在 119GFlops 左右。
小結
從上述的開發流程,OpenCL 大大的解放了 FPGAer 的開發周期,并且對于軟件開發者,也比較容易上手。這是他的優勢,但是目前開發過程中,還是存在一些問題,如:編譯器優化不足,相比 RTL 寫的性能存在差距;編譯到 Device 端時間太長。不過這些隨著行業的發展,一定會慢慢的進步。
? ? ? ?責任編輯:pj
 電子發燒友App
電子發燒友App

























評論