Particle Filter - Kidnapped vehicle project

1. Definition of Particle Filter

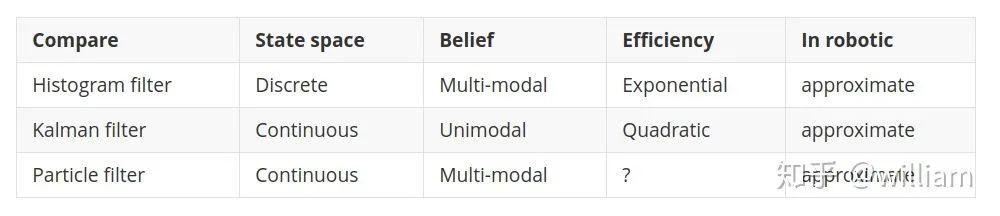
粒子濾波器是貝葉斯濾波器或馬爾可夫定位濾波器的實現。粒子過濾器基于“適者生存的原理”主要用于解決定位問題。粒子濾波的優勢在于易于編程并且靈活。 三種濾波器的性能對比:

?

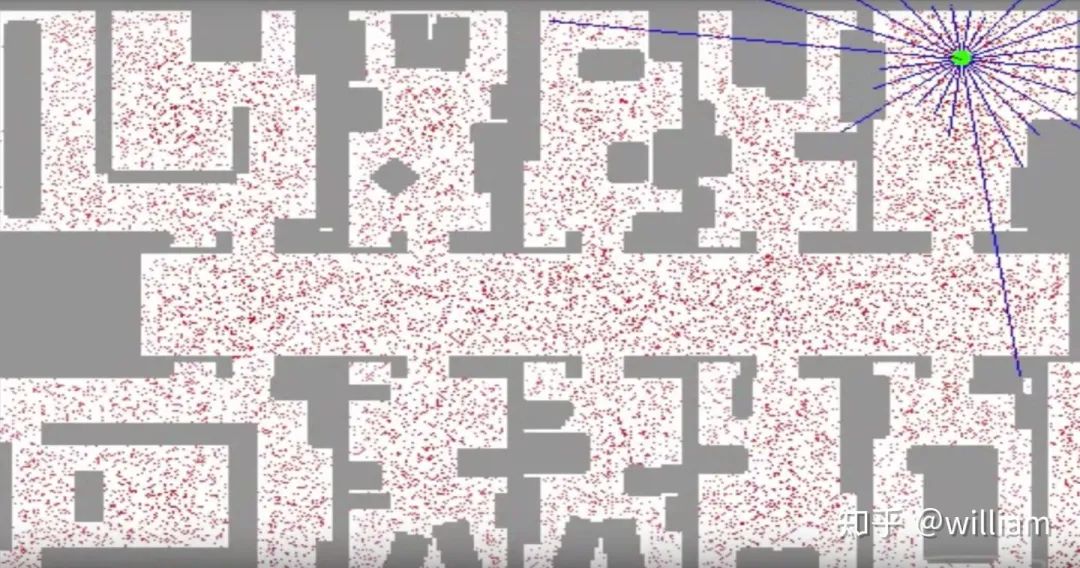
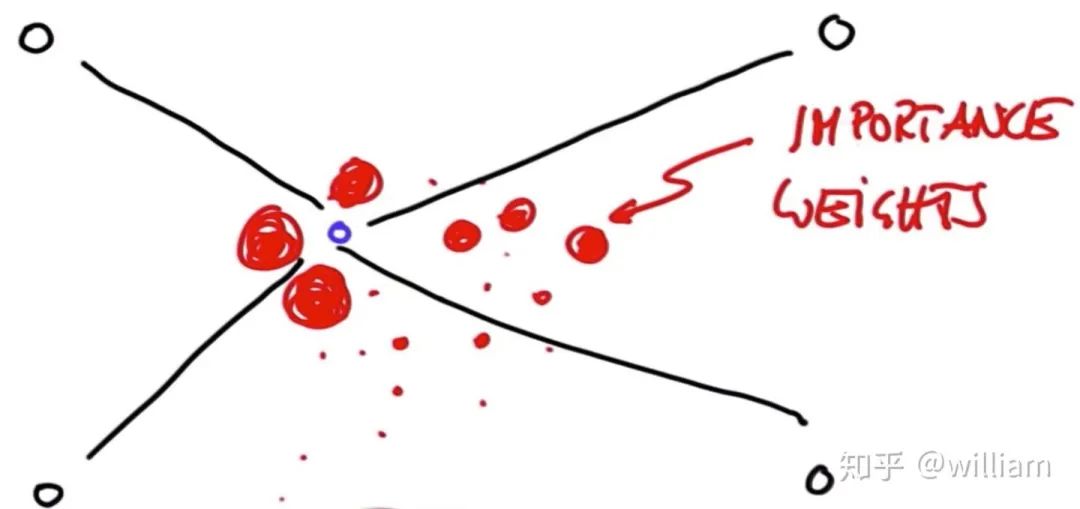
? 正如你在上面的圖片中看到的，紅點是對機器人可能位置的離散猜測。每個紅點都有 x 坐標、 y 坐標和方向。粒子濾波器是由幾千個這樣的猜測組成的機器人后驗信度表示。一開始，粒子是均勻分布的，但過濾器使他們生存的比例正比于粒子與傳感器測量的一致性。

權重(Weights)：

粒子濾波器通常攜帶離散數量的粒子。每個粒子都是一個包含 x 坐標、 y 坐標和方向的矢量。顆粒的存活取決于它們與傳感器測量結果的一致性。一致性是基于實際測量和預測測量之間的匹配度來衡量的，這種匹配度稱為權重。 ?

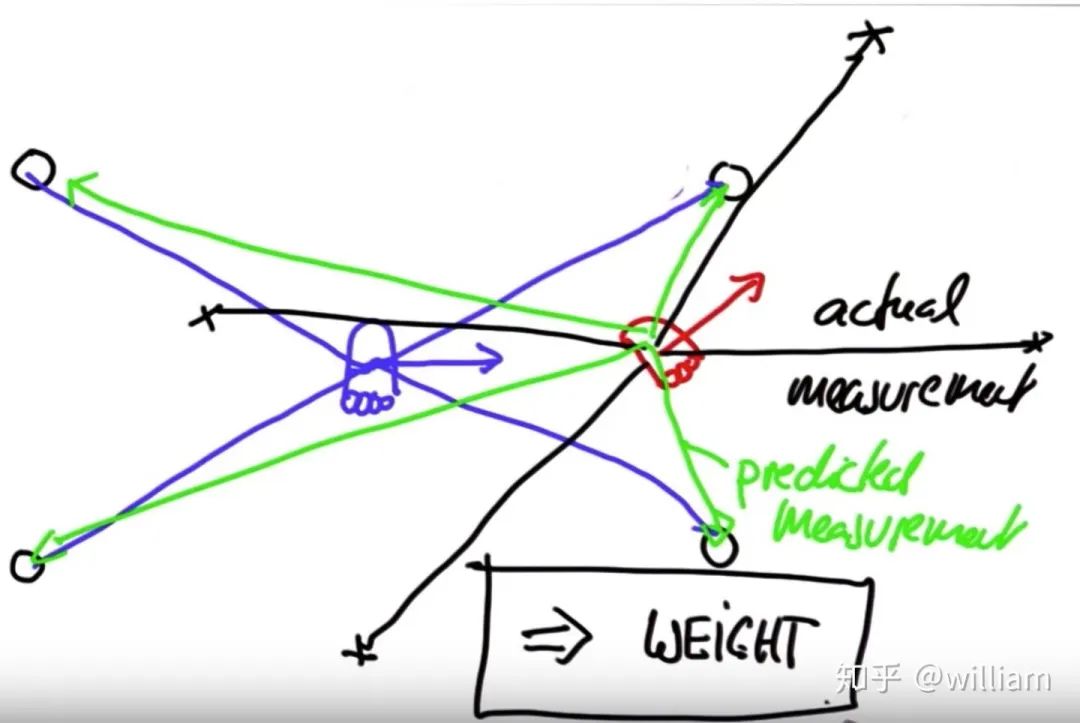
? 權重意味著粒子的實際測量與預測測量的接近程度。在粒子濾波器中，粒子權重越大，生存概率越高。換句話說，每個粒子的生存概率與權重成正比。 ?

重采樣(Resampling)

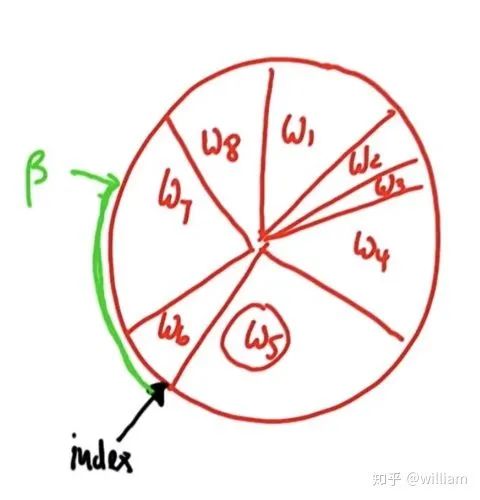
重采樣技術是用于從舊粒子中隨機抽取N個新粒子，并根據重要權重按比例進行置換。重采樣后，權重較大的粒子可能會停留下來，其他粒子可能會消失。粒子聚集在后驗概率比較高的區域。 為了進行重采樣，采用了重采樣輪技術. ?

?

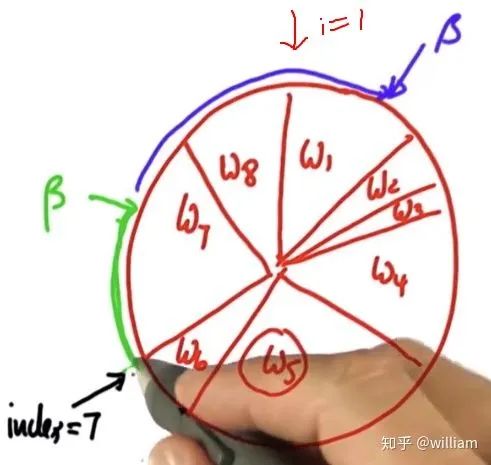
? 原理：每個粒子被選中的概率都和這個粒子輪所占的周長成正比，權重大的粒子有更多的機會被選中。 初始index為6，假設隨機的beta= 0 + 隨機權重> w6, 則index +1，beta=beta-w6. 此時beta < w7, 7號粒子被選中添加到倉庫中。之后進行下一輪循環，此時beta 和 index 仍然保留前一輪循環的值, beta= beta + 隨機權重 > w7 + w8, 因此index遞增兩次，到達index=1，此時w1 > beta, w1被選中放入倉庫中, 隨后進行下一輪循環。 重采樣的代碼：

p3 = []
index= int(random.random()*N)
beta=0.0
mw=max(w)
for i in range(N):
    beta +=random.random()*2.0*mw
    while beta>w[index]:
        beta-=w[index]
        index=(index+1)%N
    p3.append(p[index])
p=p3

?2. Particle Filters implementation

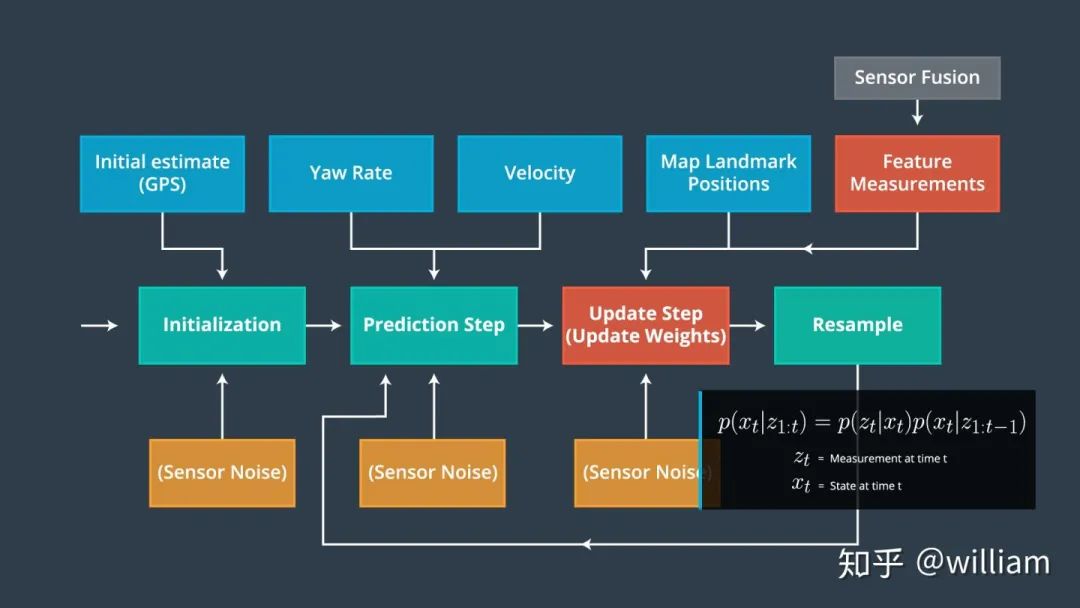
? 粒子過濾器有四個主要步驟:

初始化步驟: 我們從 GPS 輸入估計我們的位置。在這個過程中的后續步驟將完善這個估計，以定位我們的車輛

預測步驟: 在預測步驟中，我們添加了所有粒子的控制輸入(偏航速度和速度)

粒子權重更新步驟: 在更新步驟中，我們使用地圖地標位置和特征的測量更新粒子權重

重采樣步驟: 在重采樣期間，我們將重采樣 m 次(m 是0到 length_of_particleArray的范圍)繪制粒子 i (i 是粒子index)與其權重成正比。這一步使用了重采樣輪技術。

新的粒子代表了貝葉斯濾波后驗概率。我們現在有一個基于輸入證明的車輛位置的精確估計。

偽代碼：

1. 初始化步驟:

粒子過濾器的第一件事就是初始化所有的粒子。在這一步，我們必須決定要使用多少粒子。一般來說，我們必須拿出一個好的數字，因為如果不會太小，將容易出錯，如果太多會拖慢貝葉斯濾波器的速度。傳統的粒子初始化方式是把狀態空間劃分成一個網格，并在每個單元格中放置一個粒子，但這種方式只能適合小狀態空間，如果狀態空間是地球，這是不合適的。因此用 GPS位置輸入來初始估計我們的粒子分布是最實用的。值得注意的是，所有傳感器的測量結果必然伴隨著噪聲，為了模擬真實的噪聲不可控情況，應考慮給本項目的初始 GPS 位置和航向添加高斯噪聲。 項目的最終初始化步驟代碼：
void ParticleFilter::init(double x, double y, double theta, double std[]) {

    /**
     * TODO: Set the number of particles. Initialize all particles to
     *   first position (based on estimates of x, y, theta and their uncertainties
     *   from GPS) and all weights to 1.
     * TODO: Add random Gaussian noise to each particle.
     * NOTE: Consult particle_filter.h for more information about this method
     *   (and others in this file).
     */

    if (is_initialized) {
        return;
    }
    num_particles = 100;  // TODO: Set the number of particle

    double std_x = std[0];
    double std_y = std[1];
    double std_theta = std[2];

    // Normal distributions
    normal_distribution dist_x(x, std_x);
    normal_distribution dist_y(y, std_y);
    normal_distribution dist_theta(theta, std_theta);

    // Generate particles with normal distribution with mean on GPS values.
    for (int i = 0; i < num_particles; ++i) {
        Particle pe;
        pe.id = i;
        pe.x = dist_x(gen);
        pe.y = dist_y(gen);
        pe.theta = dist_theta(gen);
        pe.weight = 1.0;
        particles.push_back(pe);
        
    }
    is_initialized = true;
}

? 2. 預測步驟： 現在我們已經初始化了粒子，是時候預測車輛的位置了。在這里，我們將使用下面的公式來預測車輛將在下一個時間步驟，通過基于偏航速度和速度的更新，同時考慮高斯傳感器噪聲。 ?

? 項目的最終預測步驟代碼:

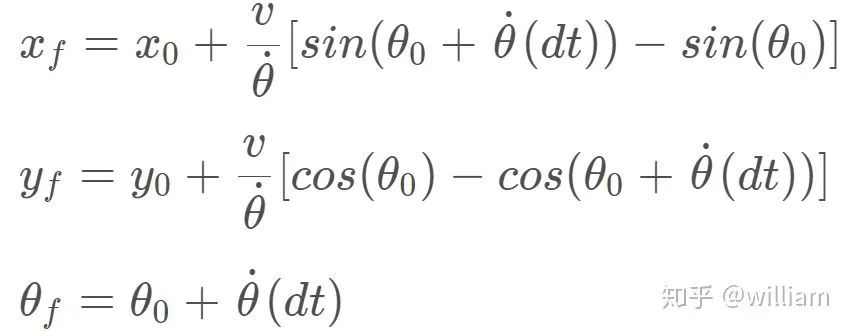
for (int i = 0; i < num_particles; i++) { if (fabs(yaw_rate) >= 0.00001) { particles[i].x += (velocity / yaw_rate) * (sin(particles[i].theta + yaw_rate * delta_t) - sin(particles[i].theta)); particles[i].y += (velocity / yaw_rate) * (cos(particles[i].theta) - cos(particles[i].theta + yaw_rate * delta_t)); particles[i].theta += yaw_rate * delta_t; } else { particles[i].x += velocity * delta_t * cos(particles[i].theta); particles[i].y += velocity * delta_t * sin(particles[i].theta); } // Add noise particles[i].x += disX(gen); particles[i].y += disY(gen); particles[i].theta += angle_theta(gen); }

3. 更新步驟:

現在，我們已經將速度和偏航率測量輸入納入到我們的過濾器中，我們必須更新基于激光雷達和雷達地標讀數的粒子權重。 更新步驟有三個主要步驟:

Transformation

Association

Update Weights

轉換 (Transformation) 我們首先需要將汽車的測量數據從當地的汽車坐標系轉換為地圖上的坐標系。

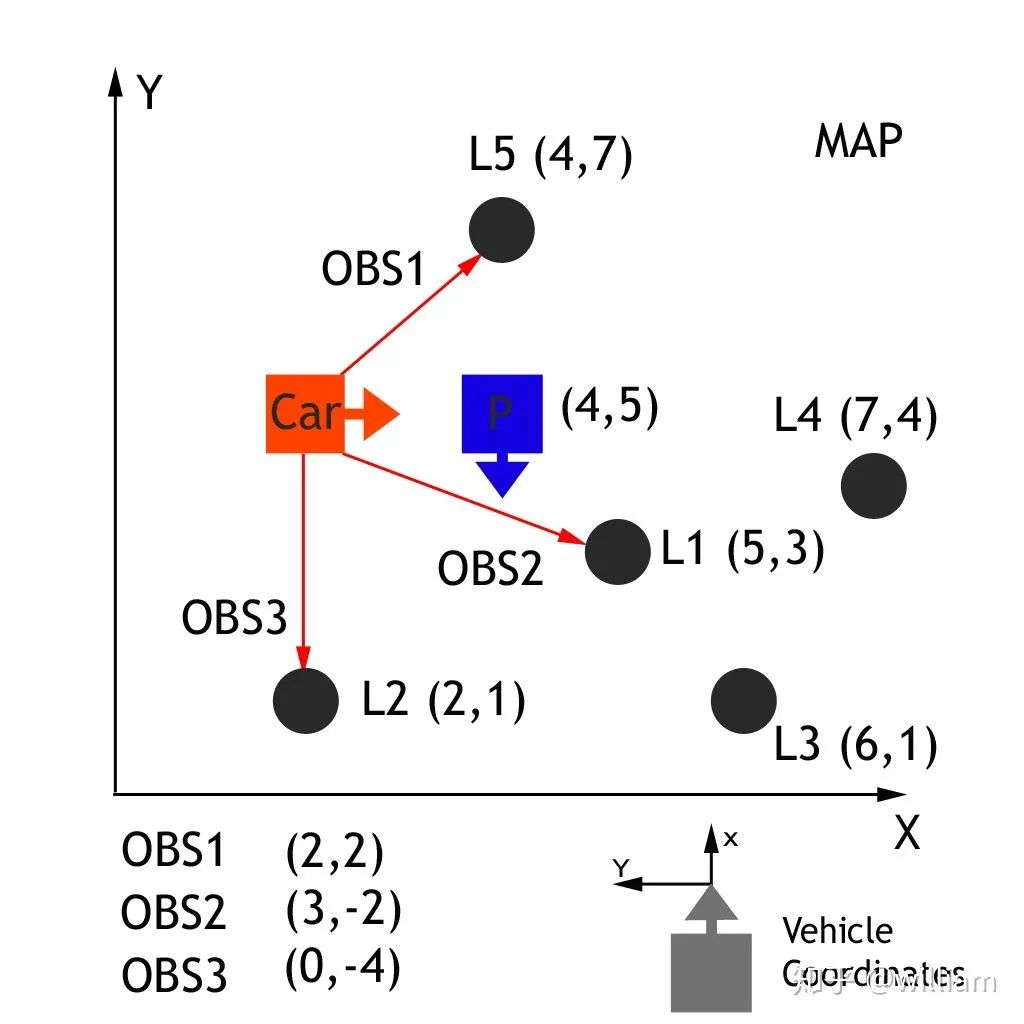
通過傳遞車輛觀測坐標(xc 和 yc)、地圖粒子坐標(xp 和 yp)和我們的旋轉角度(- 90度) ，通過齊次變換矩陣，車輛坐標系中的觀測值可以轉換為地圖坐標(xm 和 ym) 。這個齊次的變換矩陣，如下所示，執行旋轉和平移。

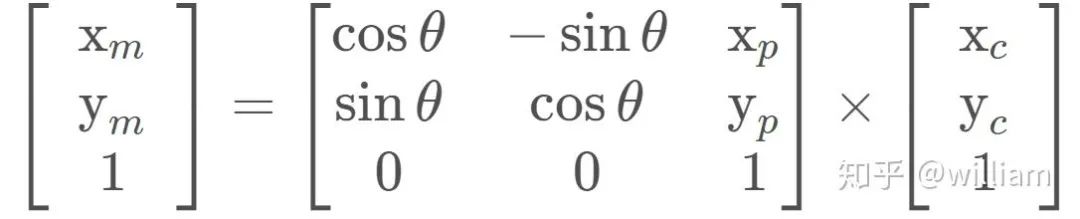
矩陣乘法的結果是:

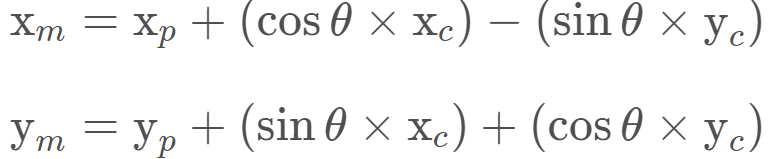
代碼

 double x_part, y_part, x_obs, y_obs, theta;
  double x_map;
 x_map = x_part + (cos(theta) * x_obs) - (sin(theta) * y_obs);
  double y_map;
 y_map = y_part + (sin(theta) * x_obs) + (cos(theta) * y_obs);

備注: 黑色方框是一個粒子，我們需要更新他的權重，(4,5) 是它在地圖坐標中的位置，它的航向是(-90度)，由于傳感器對路標的測量結果是基于車輛本身坐標，因此我們要把車輛的觀察數據轉換為地圖坐標。如L1路標的真實地圖坐標是(5,3)，車輛傳感器測得的OBS2的車輛坐標為(2,2), 經過齊次矩陣轉換后的地圖坐標是(6,3), 現在我們就可以將測量結果與真實結果聯系起來，匹配現實世界中的地標, 從而更新黑色方框粒子的權重。
?聯系 (Association )

聯系問題是在現實世界中地標測量與物體匹配的問題，如地圖地標. 我們的最終目標是為每個粒子找到一個權重參數，這個權重參數代表這個粒子與實際汽車在同一位置的匹配程度。

現在已經將觀測值轉換為地圖的坐標空間，下一步是將每個轉換后的觀測值與一個地標識符關聯起來。在上面的地圖練習中，我們總共有5個地標，每個都被確定為 L1，L2，L3，L4，L5，每個都有一個已知的地圖位置。我們需要將每個轉換觀察 TOBS1，TOBS2，TOBS3與這5個識別符之一聯系起來。為了做到這一點，我們必須將最接近的地標與每一個轉化的觀察聯系起來。
TOBS1?= (6,3),?TOBS2?= (2,2) and?TOBS3?= (0,5). OBS1匹配L1，OBS2匹配L2，OBS3匹配L2或者L5(距離相同)。
下面的例子來解釋關于數據關聯的問題。

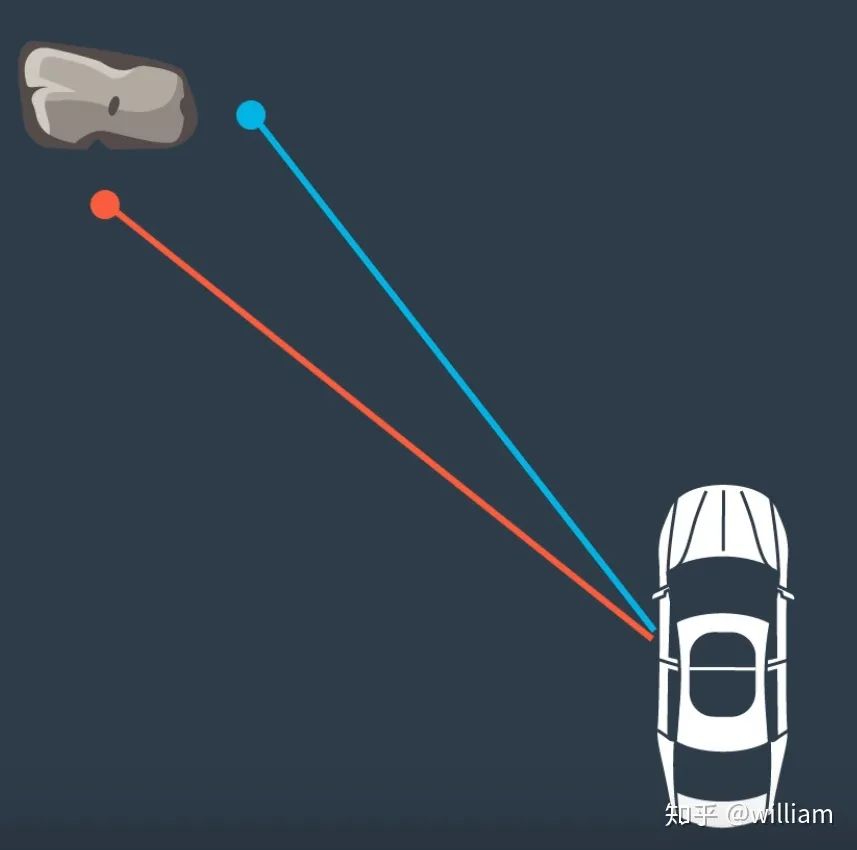
在這種情況下，我們有兩個激光雷達測量巖石。我們需要找出這兩個測量值中，哪一個與巖石相對應。如果我們估計，任何測量是真實的，汽車的位置將根據我們選擇的測量是不同的。也就是說，根據路標選擇的不同, 最終確定的車輛位置也會不同。
由于我們有多個測量的地標，我們可以使用最近鄰技術找到正確的一個。

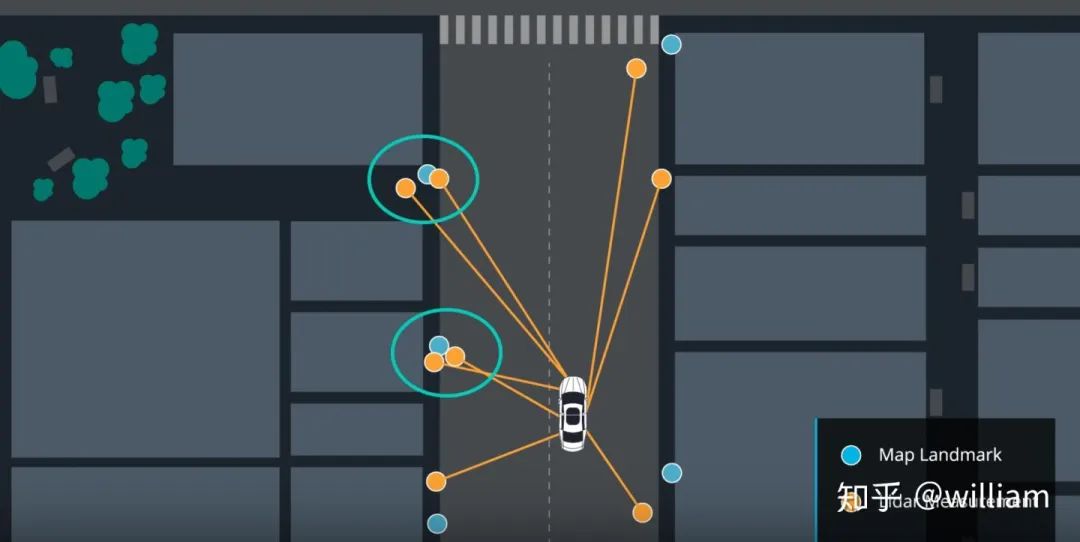
在這種方法中，我們將最接近的測量作為正確的測量。

最緊鄰法的優缺點:

更新權重 (update weights)
現在我們已經完成了測量轉換和關聯，我們有了計算粒子最終權重所需的所有部分。粒子的最終權重將計算為每個測量的多元-高斯概率密度的乘積。
多元-高斯概率密度有兩個維度，x 和 y。多元高斯分布的均值是測量的相關地標位置，多元高斯分布的標準差是由我們在 x 和 y 范圍內的初始不確定度來描述的。多元-高斯的評估基于轉換后的測量位置。多元高斯分布的公式如下。

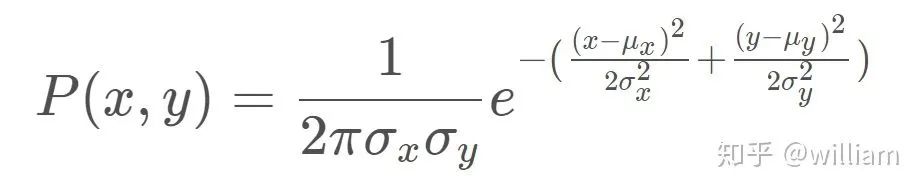
備注：x, y 是地圖坐標系的觀測值，μx,?μy是最近的路標的地圖坐標。如對于OBS2 (x,y) =(2,2), (μx,?μy)= (2,1)
誤差計算公式：

?

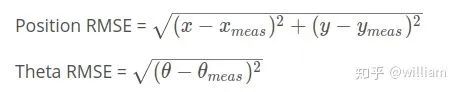
其中x, y, theta代表最好的粒子位置，xmeas, ymeas, thetameas代表真實值

?

?

?

3. Project Demo

編輯：黃飛

?