需要了解哪一些神經網絡架構

為什么需要機器學習？

有些任務直接編碼較為復雜，我們不能處理所有的細微之處和簡單編碼，因此，機器學習很有必要。相反，我們向機器學習算法提供大量數據，讓算法不斷探索數據并構建模型來解決問題。比如：在新的雜亂照明場景內，從新的角度識別三維物體；編寫一個計算信用卡交易詐騙概率的程序。

機器學習方法如下：它沒有為每個特定的任務編寫相應的程序，而是收集大量事例，為給定輸入指定正確輸出。算法利用這些事例產生程序。該程序與手寫程序不同，可能包含數百萬的數據量，也適用于新事例以及訓練過的數據。若數據改變，程序在新數據上訓練且被更新。大量的計算比支付手寫程序要便宜的多。

機器學習的應用如下：

模式識別：識別實際場景的面部或表情、語言識別。

識別異常：信用卡交易順序異常，核電廠傳感器讀數模式異常。

預測：未來股價或貨幣匯率，個人觀影喜好。

什么是神經網絡？神經網絡

神經網絡是一種通用機器學習模型，是一套特定的算法集，在機器學習領域掀起了一場變革，本身就是普通函數的逼近，可以應用到任何機器學習輸入到輸出的復雜映射問題。一般來說，神經網絡架構可分為3類：

前饋神經網絡：是最常見的類型，第一層為輸入，最后一層為輸出。如果有多個隱藏層，則稱為“深度”神經網絡。它能夠計算出一系列事件間相似轉變的變化，每層神經元的活動是下一層的非線性函數。

循環神經網絡：各節點之間構成循環圖，可以按照箭頭的方向回到初始點。循環神經網絡具有復雜的動態，難以訓練，它模擬連續數據，相當于每個時間片段具有一個隱藏層的深度網絡，除了在每個時間片段上使用相同的權重，也有輸入。網絡可以記住隱藏狀態的信息，但是很難用這點來訓練網絡。

對稱連接網絡：和循環神經網絡一樣，但單元間的連接是對稱的（即在兩個方向的連接權重相同），它比循環神經網絡更容易分析，但是功能受限。沒有隱藏單元的對稱連接的網絡被稱為“Hopfiels網絡”，有隱藏單元的對稱連接的網絡則被稱為“波茲曼機器”。

一、感知機（Perceptron）

作為第一代神經網絡，感知機是只有一個神經元的計算模型。首先將原始輸入矢量轉化為特征矢量，再用手寫程序定義特征，然后學習如何對每個特征加權得到一個標量，如果標量值高于某一閾值，則認為輸入矢量是目標類的一個積極樣例。標準的感知機結構是前饋模型，即輸入傳送到節點，處理后產生輸出結果：從底部輸入，頂部輸出，如下圖所示。但也有其局限性：一旦確定了手寫編碼特征，在學習上就受到了較大限制。這對感知器來說是毀滅性的，盡管轉換類似于翻譯，但是模式識別的重點是識別模式。如果這些轉換形成了一個組，學習的感知器部分不能學會識別，所以需要使用多個特征單元識別子模式的轉換。

沒有隱藏單元的網絡在輸入輸出映射建模上也有很大局限性。增加線性單元層也解決不了，因為線性疊加依然是線性的，固定的非線性輸出也不能建立這種映射。因此需要建立多層自適應的非線性隱藏單元。

二、卷積神經網絡（Convolutional Neural Network）

一直以來，機器學習研究廣泛集中在對象檢測上，但仍有諸多因素使其難以識別

識別對象：

對象分割、遮擋問題；

照明影響像素強度；

物體以各種不同的形式展現；

相同功能的對象具有不同的物理形狀；

視覺不同帶來的變化；

維度跳躍問題。

復制特征方法是當前CNN用于目標檢測的主要方法，大規模的復制不同位置上相同的特征檢測圖，大大減少了要學習的自由參數數量。它使用不同的特征類型，每種類型都有自己的復制檢測圖，也允許以各種方式表示每個圖像塊。

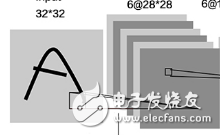
CNN可用于手寫數字識別到3D對象識別等，但從彩色圖像中識別對象比手寫數字識別要復雜，它的類別、像素是數字的100倍（1000 vs 100，256*256彩色vs28*28灰度）。

2012年的ILSVRC-2012競賽中的ImageNet提供一個包含120萬張高分辨率訓練圖像的數據集。測試圖像沒有標注，參賽者需要識別圖像中對象的類型。獲勝者 Alex Krizhevsky開發了一個深度卷積神經網絡，除了一些最大池化層，架構還有7個隱藏層，前面都是卷積層，最后2層是全局連接。激活函數在每個隱藏層都是線性單元，比邏輯單元速度更快，還使用競爭性規范標準抑制隱藏活動，有助于強度變化。硬件上，在兩個Nvidia GTX 580 GPU（超過1000個快速內核）上使用一個高效卷積網絡實現，非常適合矩陣乘法，具有很高的內存帶寬。

三、循環神經網絡（ Recurrent Neural Network）

循環神經網絡（RNN）有兩個強大的屬性可以計算任何計算機計算出來的東西：（1）允許存儲大量有效信息的分布式隱藏狀態（2）用復雜的方式允許更新隱藏狀態的非線性動態。RNN強大的計算能力和梯度消失（或爆炸）使其很難訓練。通過多層反向傳播時，若權重很小，則梯度呈指數縮小；若權重很大，則梯度呈指數增長。典型的前饋神經網絡的一些隱藏層可以應對指數效應，另一方面，在長序列RNN中，梯度容易消失（或爆照），即使有好的初始權重，也很難檢測出當前依賴于多個時間輸入的目標輸出因此很難處理遠程依賴性。

學習RNN的方法如下：

長短期記憶：用具有長期記憶值的小模塊制作RNN。

Hessian Free Optimization：使用優化器處理梯度消失問題。

回聲狀態網絡：初始化輸入→隱藏和隱藏→隱藏和輸出→隱藏鏈接，使隱藏狀態有一個巨大的弱耦合振蕩器儲備，可以選擇性的由輸入驅動。

用動量初始化：和回聲狀態網絡一樣，再用動量學習所有連接。

四、長短期記憶網絡（Long/Short Term Memory Network）

Hochreiter & Schmidhuber（1997年）構建了長短期記憶網絡，解決了獲取RNN長時間記憶問題，使用乘法邏輯線性單元設計存儲單元，只要保持“寫入”門打開，信息就會寫入并保持在單元中，也可以打開“讀取”門從中獲取數據。

RNN可以閱讀行書，筆尖的輸入坐標為（x，y，p），p代表筆是向上還是向下，輸出則為一個字符序列，使用一系列小圖像作為輸入而不是筆坐標。Graves & Schmidhuber（2009年）稱帶有LSTM的RNN是閱讀行書的最佳系統。

五、霍普菲爾德網絡（Hopfield Networks）

非線性循環網絡有很多種表現方式，較難分析：能達到穩定、震蕩或餛飩狀態這三種表現形式。Hopfield網絡是由有循環連接的二進制閾值單元組成。1982年，約翰·霍普菲爾德發現，如果連接對稱，則存在一個全局能量函數，整個網絡的每個二進制“結構”都有能量，而二進制閾值決策規則使網絡為能量函數設置一個最小值。使用這種計算類型最簡單的方法是將記憶作為神經網絡的能量最小值。使用能量最小值表示記憶給出了一個內容可尋內存，可通過了解局部內容來訪問整個項目。

每記憶一次配置，都希望能產生一個能量最小值。但若有兩個最小值就會限制Hopfield網絡容量。伊麗莎白·加德納發現有一個更好的存儲規則，它使用了所有的權重。而不是試圖一次存儲多個矢量，她通過訓練集進行多次循環，并用感知器收斂程序訓練每個單元，使該矢量的所有其它單元具有正確的狀態。

六、玻爾茲曼機（Boltzmann Machine Network）

玻爾茲曼機是一種隨機循環神經網絡，可以被看作是Hopfield網絡的隨機生成產物，是最先學習內部representations的神經網絡之一。該算法旨在最大限度地提高機器在訓練集中分配給二進制矢量的概率的乘積，相當于最大化其分配給訓練矢量的對數概率之和，方法如下：

（1）網絡沒有外部輸入時，使網絡在不同時間分布穩定；

（2）每次對可見矢量采樣。

2012年，Salakhutdinov和Hinton為玻爾茲曼機寫了有效的小批量學習程序。2014年將模型更新，稱之為受限玻爾茲曼機。

七、深度信念網絡（Deep Belief Network）

反向傳播，是人工神經網絡計算處理一批數據后每個神經元的誤差分布的標準方法，但是也存在一些問題。首先要標注訓練數據，但幾乎所有數據都沒有標注；其次，學習時間不足，這意味著隱藏層數較多的網絡較慢；第三，可能會使局部陷入最不利局面。因此，對于深度網絡來說這遠遠不夠。

無監督學習方法克服了反向傳播的限制，使用梯度方法調整權重有助于保持架構的效率和簡單性，還可以將它用于對感官輸入結構建模。特別的是，它調整權重，將產生感官輸入的生成模型概率最大化。信念網絡是由隨機變量組成的有向非循環圖，可推斷未觀測變量的狀態，還可以調整變量間的交互，使網絡更可能產生訓練數據。

早期圖形模型是專家定義圖像結構和條件概率，這些圖形是稀疏連接的，他們專注于做正確的推論，而不是學習。但對于神經網絡來說，學習是重點，其目的不在于可解釋性或稀疏連接性使推斷變得更容易。

八、深度自動編碼器（Deep Auto-encoders）

該架構提供了兩種映射方式，好像是一個做非線性降維非常好的方法，它在訓練事例的數量上是線性的（或更好的），而最終編碼模型相當緊湊和快速。然而，使用反向傳播優化深度自動編碼器很困難，若初始權重較小，反向傳播梯度會消失。我們使用無監督逐層預訓練或像回聲狀態網絡一樣認真的初始化權重。