最優(yōu)化問題是機(jī)器學(xué)習(xí)算法中非常重要的一部分,幾乎每一個(gè)機(jī)器學(xué)習(xí)算法的核心都是在處理最優(yōu)化問題。
本文中我講介紹一些機(jī)器學(xué)習(xí)領(lǐng)域中常用的且非常掌握的最優(yōu)化算法,看完本篇文章后你將會(huì)明白:
* 什么是梯度下降法?
* 如何將梯度下降法運(yùn)用到線性回歸模型中?
* 如何利用梯度下降法處理大規(guī)模的數(shù)據(jù)?
* 梯度下降法的一些技巧
梯度下降法
梯度下降法是一個(gè)用于尋找最小化成本函數(shù)的參數(shù)值的最優(yōu)化算法。當(dāng)我們無(wú)法通過分析計(jì)算(比如線性代數(shù)運(yùn)算)求得函數(shù)的最優(yōu)解時(shí),我們可以利用梯度下降法來(lái)求解該問題。
梯度下降法的直覺體驗(yàn)
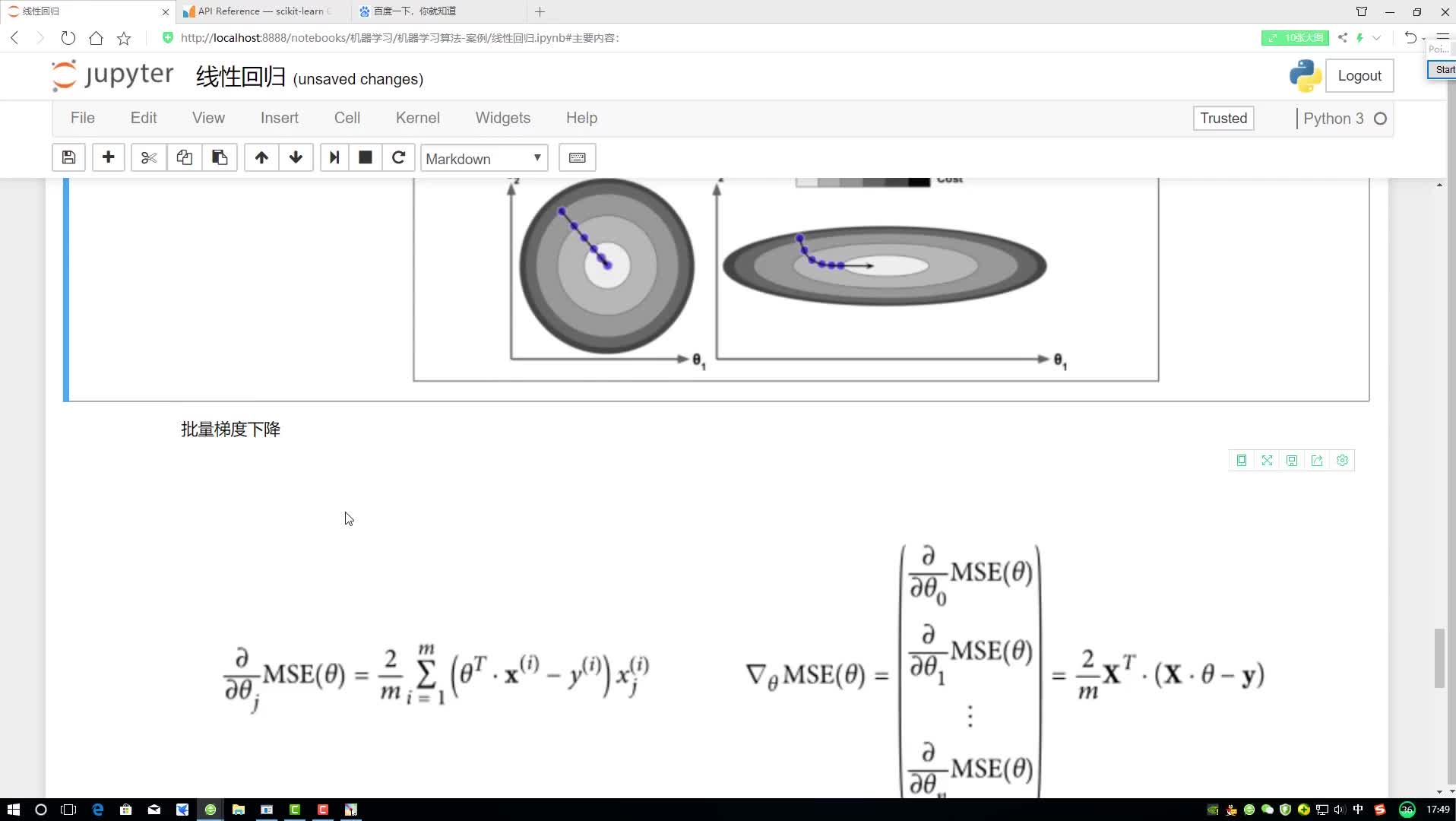
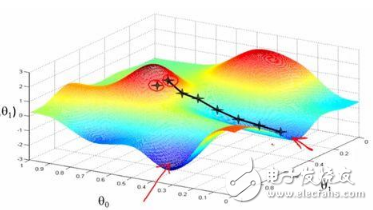
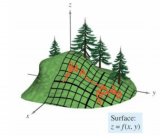
想象一個(gè)你經(jīng)常用來(lái)吃谷物或儲(chǔ)存受過的大碗,成本函數(shù)的形狀類似于這個(gè)碗的造型。
碗表面上的任一隨機(jī)位置表示當(dāng)前系數(shù)對(duì)應(yīng)的成本值,碗的底部則表示最優(yōu)解集對(duì)應(yīng)的成本函數(shù)值。梯度下降法的目標(biāo)就是不斷地嘗試不同的系數(shù)值,然后評(píng)估成本函數(shù)并選擇能夠降低成本函數(shù)的參數(shù)值。重復(fù)迭代計(jì)算上述步驟直到收斂,我們就能獲得最小成本函數(shù)值對(duì)應(yīng)的最優(yōu)解
梯度下降法的過程
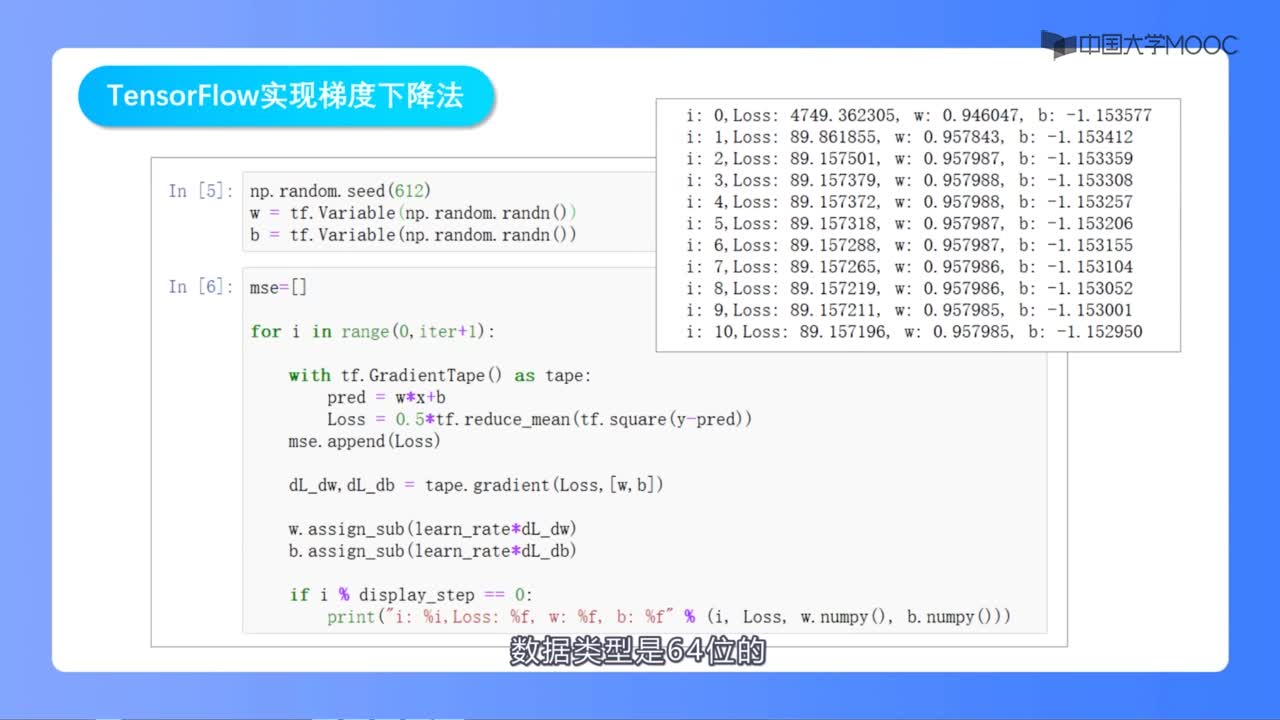
梯度下降法首先需要設(shè)定一個(gè)初始參數(shù)值,通常情況下我們將初值設(shè)為零(coefficient=0coefficient=0),接下來(lái)需要計(jì)算成本函數(shù) cost=f(coefficient)cost=f(coefficient) 或者cost=evaluate(f(coefficient))cost=evaluate(f(coefficient))。然后我們需要計(jì)算函數(shù)的導(dǎo)數(shù)(導(dǎo)數(shù)是微積分的一個(gè)概念,它是指函數(shù)中某個(gè)點(diǎn)處的斜率值),并設(shè)定學(xué)習(xí)效率參數(shù)(alpha)的值。
coefficient=coefficient?(alpha?delta) coefficient=coefficient?(alpha?delta) 重復(fù)執(zhí)行上述過程,直到參數(shù)值收斂,這樣我們就能獲得函數(shù)的最優(yōu)解。
你可以看出梯度下降法的思路多么簡(jiǎn)單,你只需知道成本函數(shù)的梯度值或者需要優(yōu)化的函數(shù)情況即可。接下來(lái)我將介紹如何將梯度下降法運(yùn)用到機(jī)器學(xué)習(xí)領(lǐng)域中。
批量梯度下降法
所有的有監(jiān)督機(jī)器學(xué)習(xí)算法的目標(biāo)都是利用已知的自變量(X)數(shù)據(jù)來(lái)預(yù)測(cè)因變量(Y)的值。所有的分類和回歸模型都是在處理這個(gè)問題。
機(jī)器學(xué)習(xí)算法會(huì)利用某個(gè)統(tǒng)計(jì)量來(lái)刻畫目標(biāo)函數(shù)的擬合情況。雖然不同的算法擁有不同的目標(biāo)函數(shù)表示方法和不同的系數(shù)值,但是它們擁有一個(gè)共同的目標(biāo)——即通過最優(yōu)化目標(biāo)函數(shù)來(lái)獲取最佳參數(shù)值。
線性回歸模型和邏輯斯蒂回歸模型是利用梯度下降法來(lái)尋找最佳參數(shù)值的經(jīng)典案例。
我們可以利用多種衡量方法來(lái)評(píng)估機(jī)器學(xué)習(xí)模型對(duì)目標(biāo)函數(shù)的擬合情況。成本函數(shù)法是通過計(jì)算每個(gè)訓(xùn)練集的預(yù)測(cè)值和真實(shí)值之間的差異程度(比如殘差平方和)來(lái)度量模型的擬合情況。
我們可以計(jì)算成本函數(shù)中每個(gè)參數(shù)所對(duì)應(yīng)的導(dǎo)數(shù)值,然后通過上述的更新方程進(jìn)行迭代計(jì)算。
在梯度下降法的每一步迭代計(jì)算后,我們都需要計(jì)算成本函數(shù)及其導(dǎo)數(shù)的情況。每一次的迭代計(jì)算過程就被稱為一批次,因此這個(gè)形式的梯度下降法也被稱為批量梯度下降法。
批量梯度下降法是機(jī)器學(xué)習(xí)領(lǐng)域中常見的一種梯度下降方法。
隨機(jī)梯度下降法
處理大規(guī)模的數(shù)據(jù)時(shí),梯度下降法的運(yùn)算效率非常低。
因?yàn)樘荻认陆捣ㄔ诿看蔚^程中都需要計(jì)算訓(xùn)練集的預(yù)測(cè)情況,所以當(dāng)數(shù)據(jù)量非常大時(shí)需要耗費(fèi)較長(zhǎng)的時(shí)間。
當(dāng)你處理大規(guī)模的數(shù)據(jù)時(shí),你可以利用隨機(jī)梯度下降法來(lái)提高計(jì)算效率。
該算法與上述梯度下降法的不同之處在于它對(duì)每個(gè)隨機(jī)訓(xùn)練樣本都執(zhí)行系數(shù)更新過程,而不是在每批樣本運(yùn)算完后才執(zhí)行系數(shù)更新過程。
隨機(jī)梯度下降法的第一個(gè)步驟要求訓(xùn)練集的樣本是隨機(jī)排序的,這是為了打亂系數(shù)的更新過程。因?yàn)槲覀儗⒃诿看斡?xùn)練實(shí)例結(jié)束后更新系數(shù)值,所以系數(shù)值和成本函數(shù)值將會(huì)出現(xiàn)隨機(jī)跳躍的情況。通過打亂系數(shù)更新過程的順序,我們可以利用這個(gè)隨機(jī)游走的性質(zhì)來(lái)避免模型不收斂的問題。
除了成本函數(shù)的計(jì)算方式不一致外,隨機(jī)梯度下降法的系數(shù)更新過程和上述的梯度下降法一模一樣。
對(duì)于大規(guī)模數(shù)據(jù)來(lái)說(shuō),隨機(jī)梯度下降法的收斂速度明顯高于其他算法,通常情況下你只需要一個(gè)小的迭代次數(shù)就能得到一個(gè)相對(duì)較優(yōu)的擬合參數(shù)。
梯度下降法的一些建議
本節(jié)列出了幾個(gè)可以幫助你更好地掌握機(jī)器學(xué)習(xí)中梯度下降算法的技巧:
繪制成本函數(shù)隨時(shí)間變化的曲線:收集并繪制每次迭代過程中所得到的成本函數(shù)值。對(duì)于梯度下降法來(lái)說(shuō),每次迭代計(jì)算都能降低成本函數(shù)值。如果無(wú)法降低成本函數(shù)值,那么可以嘗試減少學(xué)習(xí)效率值。
學(xué)習(xí)效率:梯度下降算法中的學(xué)習(xí)效率值通常為0.1,0.001或者0.0001。你可以嘗試不同的值然后選出最佳學(xué)習(xí)效率值。
標(biāo)準(zhǔn)化處理:如果成本函數(shù)不是偏態(tài)形式的話,那么梯度下降法很快就能收斂。隱蔽你可以事先對(duì)輸入變量進(jìn)行標(biāo)準(zhǔn)化處理。
繪制成本均值趨勢(shì)圖:隨機(jī)梯度下降法的更新過程通常會(huì)帶來(lái)一些隨機(jī)噪聲,所以我們可以考慮觀察10次、100次或1000次更新過程誤差均值變化情況來(lái)度量算法的收斂趨勢(shì)。
總結(jié)
本文主要介紹了機(jī)器學(xué)習(xí)中的梯度下降法,通過閱讀本文,你了解到:
最優(yōu)化理論是機(jī)器學(xué)習(xí)中非常重要的一部分。
梯度下降法是一個(gè)簡(jiǎn)單的最優(yōu)化算法,你可以將它運(yùn)用到許多機(jī)器學(xué)習(xí)算法中。
批量梯度下降法先計(jì)算所有參數(shù)的導(dǎo)數(shù)值,然后再執(zhí)行參數(shù)更新過程。
隨機(jī)梯度下降法是指從每個(gè)訓(xùn)練實(shí)例中計(jì)算出導(dǎo)數(shù)并執(zhí)行參數(shù)更新過程。
責(zé)任編輯:ct
 電子發(fā)燒友App
電子發(fā)燒友App






































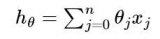
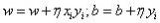

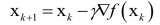










評(píng)論