徐丸絮,沈吟東
(華中科技大學 人工智能與自動化學院,湖北 武漢 430074)
摘??要:傳統的公交行程時間預測模型由于忽略了歷史時刻中的信息,導致預測精度不理想。針對公交行程時間的時序性,提出一種基于 LSTM 神經網絡的預測模型,并引入注意力(Attention)機制對其進行優化。首先,綜合考慮多種影響因素,設計了多變量 LSTM 模塊,將當前時刻的行程時間與歷史時刻數據相關聯,對其中的多維度特征進行信息提取;隨后針對單一 LSTM 網絡無法自動識別不同信息重要性的局限性,引入 Attention 機制,使模型聚焦重點信息、忽略冗雜信息;最后,采用實際公交 GPS數據驗證了該方法的有效性。實驗結果表明,與五種常見方法相比,該模型具有更高的精度。
中圖分類號:TN99?34??文獻標識碼:A
文章編號:1004?373X(2022)03?0083?05
0 引 言
公交行程時間是智能交通系統的重要組成部分,準確的行程時間信息為公交智能優化排班、實時調度、公交交叉口優先控制等提供重要依據,對公交資源動態配置、城市交通結構規劃等有深遠意義。
近年來,國內外學者對這一問題展開了廣泛研究,提出的預測模型主要包括4類:
1)卡爾曼濾波器模型[1?2]。如文獻[1]分析了異構交通條件下時間的離散化模式,以此構建了基于卡爾曼濾波器的預測模型。但是該模型考慮因素較單一,且適用于線性系統,對于高度非線性的公交行程時間預測問題并不是很合適。
2)支持向量機(SVM)模型[3?4]。如文獻[3]選取時段、天氣等7維特性構建了改進的 SVM 預測模型,并在廈門BRT?1路的數據上驗證了模型精度。但該類模型計算復雜度高,不能很好地處理大規模數據。
3)決策樹模型。如文獻[5]構建了一種基于梯度提升回歸樹(GBRT)的預測模型,測試結果比SVM和自回歸平均法的預測精度有所提高。該模型可解釋性強,但是存在模型速率低、易過擬合等問題。
4)神經網絡模型。該模型在行程時間預測問題中使用最為廣泛,如文獻[6]將螢火蟲算法與BP神經網絡結合,構建了預測模型;文獻[7]構建了面向動態站點的BP 神經網絡預測模型,實現了跨越多個站點的預測;文獻[8]通過采集到的歷史和實時數據構建了神經網絡。神經網絡能夠較好地擬合非線性問題,在行程時間預測問題上很有意義,然而公交行程時間具有時序性,即當前時刻行程時間與歷史時刻密切相關,上述模型的不足之處在于僅考慮了當前時刻的信息,沒有充分利用歷史時刻的數據,導致模型精度受限。
深度學習與傳統的學習方法相比,它具備更強大的數據學習和抽象能力。LSTM(Long Short?Term Memory)作為目前最熱門的深度學習技術之一,能夠保存歷史信息,既繼承了傳統神經網絡的優勢,又能挖掘歷史時刻數據,在處理時序問題上很有優勢[9],近幾年得到了廣泛應用。文獻[10]使用英國66個路段的數據構建了改進的LSTM模型;文獻[11]采用LSTM網絡進行預測,并與BP神經網絡進行了對比,結果證明LSTM精度更優。然而傳統的LSTM將輸入序列轉換為定長向量而保存所有的信息,使得模型記憶受限,在處理長序列問題時易丟失信息。
Attention機制的提出可以彌補這一缺陷,它能為不同信息賦予權重,加強對重要信息的記憶,忽略無關信息。近年來,結合注意力機制的神經網絡成為研究的熱點,被廣泛應用于機器翻譯、圖像分類等領域,在公交行程時間預測問題上的研究相對較少。因此,本文提出一種基于Attention機制的LSTM預測模型,利用LSTM模塊,對歷史數據中多種因素同步分析,針對LSTM的局限性,融入Attention機制,自動抽取關鍵信息,優化模型。最后與五種常見方法進行對比發現,該模型有更高的預測精度。
1 問題定義
本文旨在基于公交企業積累的大量行程時間樣本,設計一個行程時間預測方法。公交行程時間在不同日期、時段是隨機變化的,與路況、事故等動態因素密切相關[12]。由于班次之間時間間隔較短,相鄰班次之間的路段狀況具有相似性,因此歷史時刻的數據中蘊含著影響未來的信息,即當前時刻的行程時間與歷史時刻有關,由此可見,公交行程時間具有時序性,是一個前后關聯的時間序列。
根據行程時間的時序性,該問題可描述如下,由前s 個時刻的歷史行程時間序列 [yt-s,?, yt-2 , yt-1](s代表時間步長度,即歷史時刻個數)和歷史特征[xt-s,?,xt-2, xt-1]預測t時刻的公交行程時間yt,即:
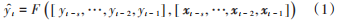
式中:xi=(xi,1,xi,2,?,xi,n)T代表第i時刻影響行程時間的多種因素的取值向量,n代表影響因素的個數;F為函數,代表預測值與輸入值之間的某種映射關系。本文的目的就是找到合適的模型用于擬合這種復雜的非線性映射。
2 公交行程時間影響因素分析
常見的LSTM模型僅考慮“歷史行程時間”這一種歷史數據[10?11],然而行程時間受多種因素影響,如果模型僅對單變量進行處理,并不能充分考慮多種影響因素的變化。因此本節對行程時間影響因素進行分析,以期得到更全面的輸入特征。
影響公交行程時間的不確定因素主要包括道路因素、交通因素、天氣情況等[13]。道路和交通因素如路段狀況、行人數量、乘客數量等信息,動態影響著行程時間;天氣情況如降雨、降雪、大霧等會影響公交速度和司機反應時間,從而影響行程時間。
根據上述行程時間影響因素分析,本文選取了行駛特征集以描述道路和交通因素,選取了天氣特征集以描述天氣因素,以此作為模型輸入。具體獲取和處理如下:
1)行駛特征集
由于路況、人流等實時信息無法直接獲取,為反映車輛行駛路段狀況、人流量等信息,選取當天是否是周末、是否是高峰期等靜態特征,同時提取車輛平均速度、車輛行駛方向等作為動態特征,用以反映實時交通狀況。
2)天氣特征集
采用網絡爬蟲獲取結構化的天氣數據,主要包含如下屬性:時間、溫度、氣壓、天氣狀況等。選取其中與行程時間密切相關的溫度和天氣狀況作為天氣特征集。
綜上所述,選取的輸入特征一共有6個,分別為當天是否是周末、是否是高峰期、車輛平均速度、車輛行駛方向、溫度、天氣狀況,即影響因素的個數n=6。
3 基于 Attention?LSTM 的公交行程時間預測模型
公交行程時間是一個典型的時間序列,LSTM網絡能自動保存歷史序列信息,更好地利用其時序性。然而不同信息對于預測時刻的影響程度是隨時間動態變化的,例如,對早晚高峰期來說,人流量對行程時間的影響要大于對平峰期的影響;單一的LSTM模型將輸入序列轉換為定長向量而保存所有的信息,并不能檢測哪些是影響當前行程時間的重要部分,降低了信息的利用率;Attention機制的加入能解決這一問題,它為模型分配不同的注意力,使模型能自動處理不同信息的重要程度。本文嘗試將LSTM與Attention機制結合,用于公交行程時間預測,本文提出的Attention?LSTM預測模型整體結構如圖1所示。
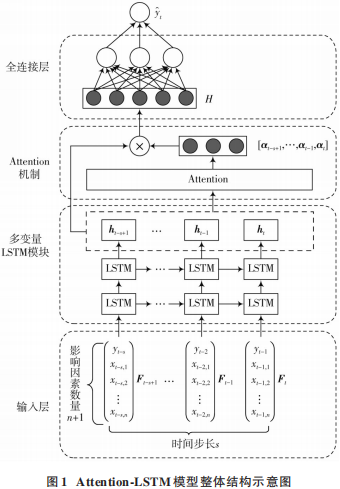
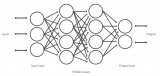
由圖1可見,該模型由4個部分組成:輸入層負責將預處理后的數據轉換成模型可讀的形式;多變量LSTM模塊負責對包含多種影響因素的輸入數據進行處理,獲取特征信息;Attention 機制負責學習一組注意力系數,對特征信息進行篩選;全連接層接收篩選后的特征信息,處理得到最終的行程時間預測結果。輸入層和全連接層是模型完成預測任務必需的組件,其結構由數據本身的維度決定,整個模型的重點部分在于多變量 LSTM模塊與Attention機制。
3.1 多變量 LSTM 模塊
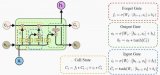
基本的LSTM網絡是由多個記憶神經元按時間次序連接而成的[14]。經典的記憶神經元內部結構如圖2所示。
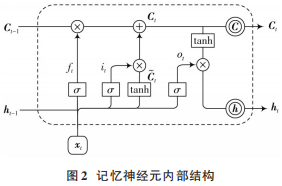
由圖2可見,記憶神經元內部由輸入門it、遺忘門ft、輸出門ot三種門結構組成,它們共同控制著信息的更新與遺忘,計算公式見式(2)~式(7):????
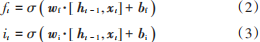
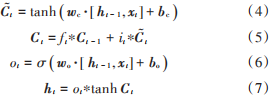
式中:σ代表sigmoid函數;Ct和Ct-1分別代表LSTM單元在t 時刻和t-1時刻的狀態;Ct 代表當前單元狀態更新值;ht和ht-1分別為當前單元和上一單元的中間狀態;wf,wi,wo,bf,bi和bo為模型訓練得到的權重矩陣和偏移量。
由此可見,LSTM網絡通過門結構對信息進行繼承,能夠實現更長期的記憶。本文利用這一特性,在基本LSTM的基礎上設計了多變量LSTM模 塊 ,該模塊由兩層LSTM網絡 堆疊而成 ,在t時刻的輸入為Ft=[yt-1, xt-1,1,xt-1,2,?,xt-1,n ]T,其不僅接收上一時刻的歷史行程時間真實值yt-1,且對代表多種影響因素的序列[xt-1,1,xt-1,2,?,xt-1,n ]T進行處理,多變量的引入使模型從更多方面接收反映行程時間的信息,可以更充分地挖掘歷史數據;最終獲得整個模塊在t時刻的輸出向量[ht-s+1,?,ht-1,ht],其中蘊含著用于行程時間預測的多維度信息。
3.2?結合 LSTM 的Attention機制
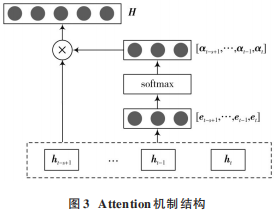
本文引入的Attention機制結構如圖3所示,其對LSTM模塊的輸出向量[ht-s+1 ,?,ht-1 ,ht]進行學習,得到一系列注意力系數[αt-s+1,?,αt-1,αt],用以表示每一中間狀態的重要程度。最后對各中間狀態加權求和得到輸出序列H,計算公式見式(8)~式(10)
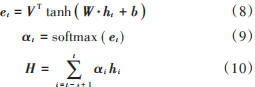
式中:V,W代表權重矩陣;b為相應的偏置值;et為計算t時刻注意力系數 αt的中間值。
由此可見,融合Attention機制后,模型可以自主學習各狀態的重要程度,從復雜的數據中提取出重要的部分。
4 實驗與分析
為了測試所提出模型的性能,基于真實數據進行實驗,并與多種常見預測模型進行對比,以驗證該模型的有效性。
4.1 數據預處理
本文采用某市290路公交車2017年1月1日—2月28日不同班次產生的GPS數據作為研究對象,該數據的每一行代表一條公交行程記錄,每一列代表不同的屬性;為了避免數據缺失對模型預測造成影響,采用缺失值的前 1天以及后 1天相同時刻的數據均值補全缺失數據。另外,為了使輸入數據數量級保持一致,采用最大最小值歸一化法,使數據都被限定在[0,1]范圍內。
4.2 模型參數設置及評價
通過多次實驗發現,當時間步長s為 9、LSTM隱含層節點數為8時模型表現最好。為了提高訓練速率,采用批量訓練的方式,每批含72組樣本數據,為了避免過擬合,在每層 LSTM 網絡后增加隨機失活(dropout)層,參數設置為0.2,選擇平均絕對誤差(MAE)作為訓練的損失函數,采用 Adam 算法對網絡進行訓練,迭代次數設置為 100次。
為評估模型的可靠性,本文同時采用平均絕對誤差(MAE)與平均絕對相對誤差(MAPE)評估模型的預測能力。具體見式(11)和式(12),其中yi表示預測值,yi表示真實值,m表示實驗所用數據總量。
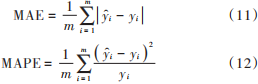
當MAE越小時,表示誤差越小;當MAPE越小時,表示預測精確度越高。
4.3 結果分析
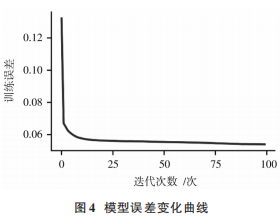
本文采用的數據集一共12157條,選擇前9000條數據作為訓練集,后3157條數據作為測試集,模型訓練過程中誤差變化趨勢如圖4所示。由圖4可知 ,Attention?LSTM模型誤差不斷下降,較快達到收斂,最終誤差降為0.544,說明訓練結果良好。
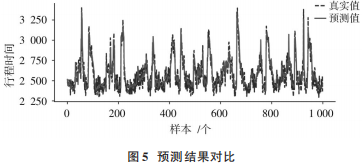
為了以更直觀的方式驗證模型預測效果,利用該模型對測試集中隨機選取的1000個樣本進行預測,結果如圖5所示。由圖5可見,所提出的模型能夠較好地擬合行程時間的劇烈變化。
為分析Attention機制的加入對模型的影響及有效性,對模型預測過程中不同時間步的注意力系數結果進行展示,如圖6所示。
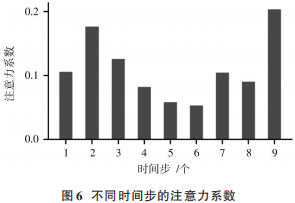
由圖6可以看出:不同時間步對行程時間的影響程度不同,注意力系數使得模型重點關注第2,3,9個時間步,而對第5,6個時間步的關注較低,由此可見,Attention機制可以使模型自動關注重要的歷史時刻,從而提高了模型對關鍵信息的篩選與利用。同時也說明,公交行程時間是一個明顯的時序性數據,模型的注意力并非集中在距離預測點較近的時間步上,而是對長時間步中的信息都有關注。
為了進一步比較提出的Attention ?LSTM模型和其他模型的預測性能,本文構造了 BPNN、RNN、LSTM、GBRT、XGBoost等五種常見預測方法,在相同的測試集上進行預測,得到的預測結果如表 1所示。
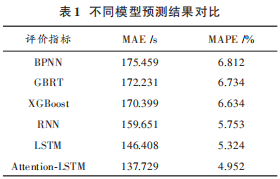
根據表1可以得到如下結論:
1)與其他幾種常見的預測模型相比,本文構建的Attention?LSTM 模型在各項指標中均為最優,在測試集中MAE=137.729,MAPE=4.952%。另外,與RNN 相比,預測精度提高了21.9s左右,精度提高了1.8%左右,證明了LSTM在處理公交行程時間這類長序列問題上的優勢;與未融入Attention機制的LSTM 模型相比,預測結果提高了8.7s左右,精度提高了0.4% 左右,再次證明了Attention機制加入的有效性。
2)基于深度循環神經網絡的這類模型(Attention?LSTM、LSTM 和 RNN)的預測性能明顯優于傳統的淺層學習方法(BPNN)和決策樹類方法(GBRT、XGBoost),其原因在于模型深度和結構的提升能夠更全面地捕捉數據中的信息,而循環神經網絡類的模型能夠很好地利用行程時間的時序性,充分利用歷史數據,使得預測精度提高,說明了深度學習在預測問題上的有效性。
5 結 語
本文針對公交行程時間的時序性,提出了融入Attention機制的LSTM預測模型。該模型利用LSTM模塊對多維度特征進行捕捉,并通過Attention機制克服了LSTM的局限性,利用模型對復雜信息進行篩選。實驗結果表明,LSTM在行程時間預測問題上很有優勢,Attention機制的引入,使模型能夠自動關注重要的歷史時刻,提高了模型的預測精度。同時,與五種常見預測方法相比,證明了該模型具有更高的預測可靠度,說明此方法具有較高的實用價值。
注:本文通訊作者為沈吟東。
參 考 文 獻
[1] KUMAR B A,VANAJAKSHI L,SUBRAMANIAN S C. Pattern?based time ? discretized method for bus travel time prediction[J]. Journal of transportation engineering, part A:systems,2017,143(6):04017012.
[2] DEESHMA M,VERMA A. Travel time modeling for bus trans?port system in Bangalore city [J]. Transportation research,2015,7(1):47?56.[3] 張洋,程恩 .基于 ε?支持向量機回歸的快速公交到站時間預測[J].廈門大學學報(自然科學版),2017,56(3):442?448.
[4] BAI C,PENG Z R,LU Q C,et al. Dynamic bus travel timeprediction models on road with multiple bus routes [J]. Compu?tational intelligence and neuroscience,2015(3):432389.
[5] 龔越,羅小芹,王殿海,等 .基于梯度提升回歸樹的城市道路行程時間預測[J].浙江大學學報(工學版),2018,52(3):453?460.
[6] 彭新建,翁小雄. 基于螢火蟲算法優化BP神經網絡的公交行程時間預測[J]. 廣西師范大學學報(自然科學版),2017,35(1):28?36.
[7] 韓勇,周林,高鵬,等 . 基于 BP 神經網絡的公交動態行程時間預測方法研究[J].中國海洋大學學報(自然科學版),2020,50(2):142?154.
[8] XIE J M,CHOI Y K. Hybrid traffic prediction scheme for intel?ligent transportation systems based on historical and real ? timedata [J]. International journal of distributed sensor networks,2017,13(11):74500.
[9] AGAFONOV A A,YUMAGANOV A S. Bus arrival time pre?diction using recurrent neural network with LSTM architecture[J]. Optical memory and neural networks,2019,28(3):222?230.
[10] DUAN Y J,YISHENG L V,WANG F Y. Travel time predic?tion with LSTM neural network [C]// 2016 IEEE 19th Interna?tional Conference on Intelligent Transportation Systems(ITSC). Rio de Janeiro,Brazil:IEEE,2016:1053?1058.
[11] 張威威,李瑞敏,謝中教 .基于深度學習的城市道路旅行時間預測[J].系統仿真學報,2017,29(10):2309?2315.
[12] 王殿海,湯月華,陳茜,等 . 基于 GPS 數據的公交站點區間行程時間可靠性影響因素[J]. 東南大學學報(自然科學版),2015,45(2):404?412.
[13] 王芳杰,王福建,王雨晨,等 .基于 LightGBM 算法的公交行程時間預測[J]. 交通運輸系統工程與信息,2018,19(2):116?121.
[14] 王志建,李達標,崔夏 .基于 LSTM 神經網絡的降雨天旅行時間預測研究[J].交通運輸系統工程與信息,2020,20(1):137?144.
作者簡介:
徐丸絮(1997—),女,江西鷹潭人,碩士研究生,研究方向為深度學習、公交行程時間預測。
沈吟東(1965—),女,安徽合肥人,博士,教授,博士生導師,研究方向為運籌與優化、公共交通規劃與調度、智能公交系統。
編輯:黃飛
?
 電子發燒友App
電子發燒友App




















評論