在機(jī)器學(xué)習(xí)和相關(guān)領(lǐng)域，人工神經(jīng)網(wǎng)絡(luò)的計算模型靈感正是來自生物神經(jīng)網(wǎng)絡(luò)：每個神經(jīng)元與其他神經(jīng)元相連，當(dāng)它興奮時，就會像相鄰的神經(jīng)元發(fā)送化學(xué)物質(zhì)，從而改變這些神經(jīng)元內(nèi)的電位；如果某神經(jīng)元的電位超過了一個閾值，那么它就會被激活（興奮），向其他神經(jīng)元發(fā)送化學(xué)物質(zhì)。人工神經(jīng)網(wǎng)絡(luò)通常呈現(xiàn)為按照一定的層次結(jié)構(gòu)連接起來的“神經(jīng)元”，它可以從輸入的計算值，進(jìn)行分布式并行信息處理的算法數(shù)學(xué)模型。這種網(wǎng)絡(luò)依靠系統(tǒng)的復(fù)雜程度，通過調(diào)整內(nèi)部大量節(jié)點(diǎn)之間相互連接的關(guān)系，從而達(dá)到處理信息的目的。并且它也被用于估計或可以依賴于大量的輸入和一般的未知近似函數(shù)，來最大化的擬合現(xiàn)實(shí)中的實(shí)際數(shù)據(jù)，提高機(jī)器學(xué)習(xí)預(yù)測的精度。

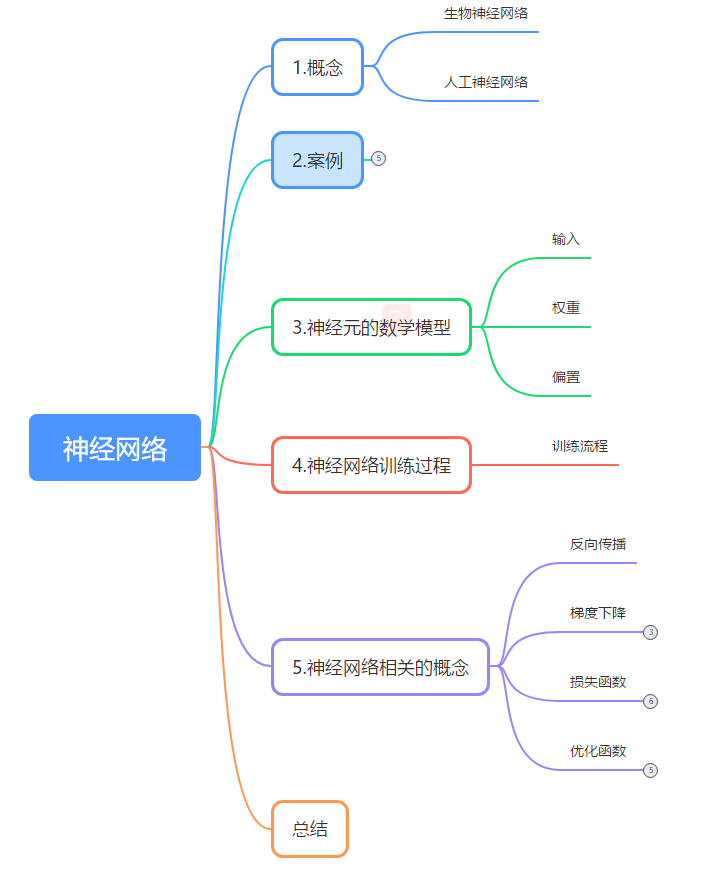
概要

單純的講神經(jīng)網(wǎng)絡(luò)的概念有些抽象，先通過一個實(shí)例展示一下機(jī)器學(xué)習(xí)中的神經(jīng)網(wǎng)絡(luò)進(jìn)行數(shù)據(jù)處理的完整過程。

01神經(jīng)網(wǎng)絡(luò)的實(shí)例

1.1 案例介紹

實(shí)例：訓(xùn)練一個神經(jīng)網(wǎng)絡(luò)模型擬合 廣告投入（TV,radio,newspaper 3種方式）和銷售產(chǎn)出的關(guān)系，實(shí)現(xiàn)根據(jù)廣告投放來預(yù)測銷售情況。

樣本數(shù)據(jù)：參考下圖

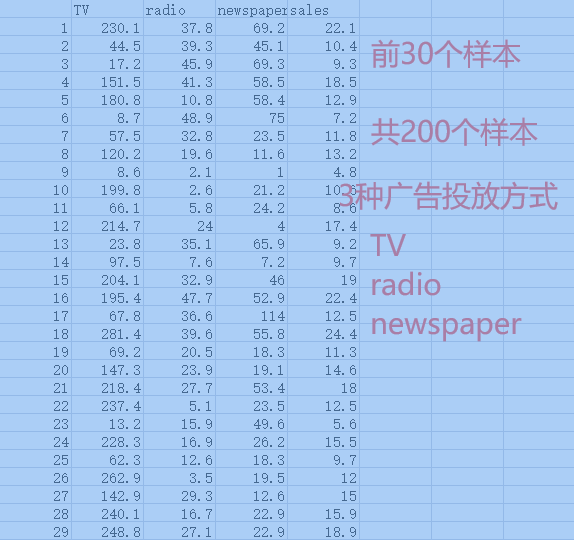
樣本數(shù)據(jù)

TV，radio和newspaper是樣本數(shù)據(jù)的3個特征，sales是樣本標(biāo)簽。

1.2 準(zhǔn)備數(shù)據(jù)

?

#添加引用
import tensorflow as tf
import pandas as pd
import numpy as np
#加載數(shù)據(jù)
data = pd.read_csv('../dataset/Advertising.csv')#pd 是數(shù)據(jù)分析庫pandas
# 建立模型 根據(jù)tv，廣播，報紙投放額 預(yù)測銷量
print(type(data),data.shape)### (200, 5)
#取特征 x取值除去第一列和最后一列的值取出所有投放廣告的值
x = data.iloc[:,1:-1]#200*3
#y取值最后一列銷量的值 標(biāo)簽
y = data.iloc[:,-1] #200*1

?

1.3 構(gòu)建一個神經(jīng)網(wǎng)絡(luò)

建立順序模型：Sequential

隱藏層：一個多層感知器(隱含層10層Dense(10),形狀input_shape=(3,)，對應(yīng)樣本的3個特征列,激活函數(shù)activation="relu")，

輸出層：標(biāo)簽是一個預(yù)測值，緯度是1

?

model = tf.keras.Sequential([tf.keras.layers.Dense(10,input_shape=(3,),activation="relu"),
tf.keras.layers.Dense(1)])

?

模型結(jié)構(gòu) print(model.summary())

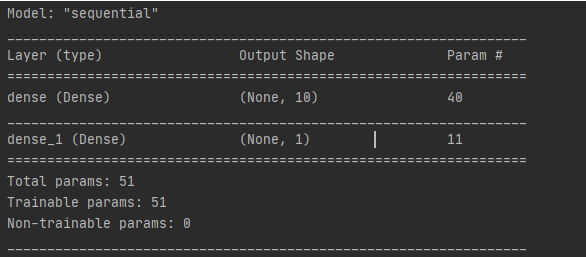
模型結(jié)構(gòu)

說明：

1）keras的模型，Sequential表示順序模型，因?yàn)槭侨B接的，選擇順序模型

2）tf.keras.layers.Dense 是添加網(wǎng)絡(luò)層數(shù)的API

3）隱藏層參數(shù) 40個，10個感知器（神經(jīng)元），每個感知器有4個參數(shù)（w1,w2,w3,b），總共10*4 = 40

4）輸出層參數(shù)11個，1個感知器（神經(jīng)元），參數(shù)(w1,w2,w3,w4,w5,w6,w7,w8,w9,w10,b)共11個

5）模型參數(shù)個數(shù)總計40+11 = 51個

1.4 給創(chuàng)建的模型加入優(yōu)化器和損失函數(shù)

# 優(yōu)化器adam，線性回歸模型損失函數(shù)為均方差（mse）

model.compile(optimizer="adam",loss="mse")

1.5啟動訓(xùn)練

# 訓(xùn)練模型

model.fit(x,y,epochs=100)

x 是樣本的特征；y 是樣本的標(biāo)簽

epochs?是梯度下降中的概念，當(dāng)一個完整的數(shù)據(jù)集通過了神經(jīng)網(wǎng)絡(luò)一次并且返回了一次，這個過程稱為一個?epoch；當(dāng)一個 epoch 對于計算機(jī)而言太龐大的時候，就需要把它分成多個小塊，需要設(shè)置batch_size,這部分內(nèi)容在后面的梯度下降章節(jié)再詳細(xì)介紹。

1.6使用模型預(yù)測

# 使用該模型在現(xiàn)有數(shù)據(jù)上預(yù)測前10個樣本的銷量

test = data.iloc[:10,1:-1]

print('測試值',model.predict(test))

以上步驟展示一個神經(jīng)網(wǎng)絡(luò)模型的構(gòu)建，訓(xùn)練和預(yù)測的全部過程，下面再介紹一下原理。

02神經(jīng)元的數(shù)學(xué)模型

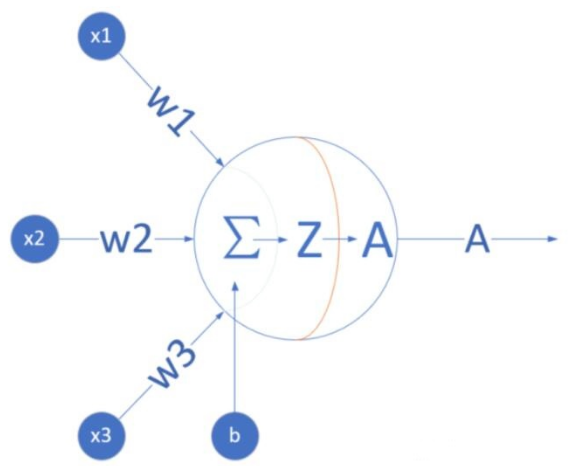
神經(jīng)元的數(shù)學(xué)模型

輸入 input

(x1, x2, x3) 是外界輸入信號，一般是一個訓(xùn)練數(shù)據(jù)樣本的多個屬性/特征，可以理解為實(shí)例中的3種廣告投放方式。

權(quán)重 weights

(w1,w2,w3) 是每個輸入信號的權(quán)重值，以上面的 (x1,x2,x3)的例子來說，x1的權(quán)重可能是 0.92，x2的權(quán)重可能是 0.2，x3的權(quán)重可能是 0.03。當(dāng)然權(quán)重值相加之后可以不是 1。

偏移bias

還有個 b 是怎么來的？一般的書或者博客上會告訴你那是因?yàn)?y=wx+by，b 是偏移值，使得直線能夠沿 Y軸上下移動。從生物學(xué)上解釋，在腦神經(jīng)細(xì)胞中，一定是輸入信號的電平/電流大于某個臨界值時，神經(jīng)元細(xì)胞才會處于興奮狀態(tài)，這個 b 實(shí)際就是那個臨界值。亦即當(dāng)：w1*x1+w2*x2+w3*x3>=t?時,該神經(jīng)元細(xì)胞才會興奮。我們把t挪到等式左側(cè)來，變成(?t)，然后把它寫成 b，變成了：w1*x1+w2*x2+w3*x3+b>=0

03神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程

還是以前面的廣告投放為例，神經(jīng)網(wǎng)絡(luò)訓(xùn)練之前需要先搭建一個網(wǎng)絡(luò)，然后填充數(shù)據(jù)（加入含特征和標(biāo)簽的樣本數(shù)據(jù)）訓(xùn)練，訓(xùn)練的過程就是不斷更新權(quán)重w和偏置b的過程。輸入有10層，每一層的特征個數(shù)由樣本確定（實(shí)例中的3種廣告投放方式即3個特征列），每一層參數(shù)就有4個（w1,w2,w3,b），全連接時10層相當(dāng)于10*4=40 個參數(shù)。如下是一個單層神經(jīng)網(wǎng)絡(luò)模型，但是有2個神經(jīng)元。

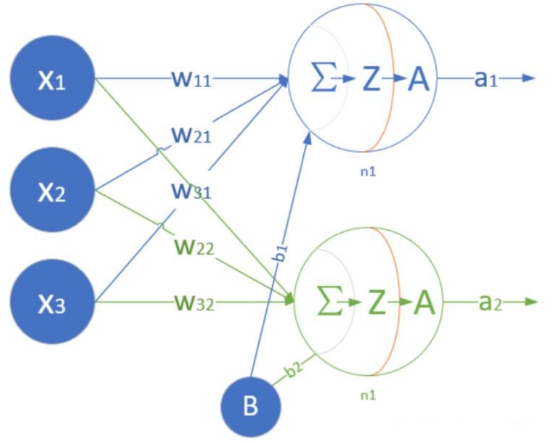
2個神經(jīng)元的模型

訓(xùn)練流程

訓(xùn)練的過程就是不斷更新權(quán)重w和偏置b的過程，直到找到穩(wěn)定的w和b 使得模型的整體誤差最小。具體的流程如下，

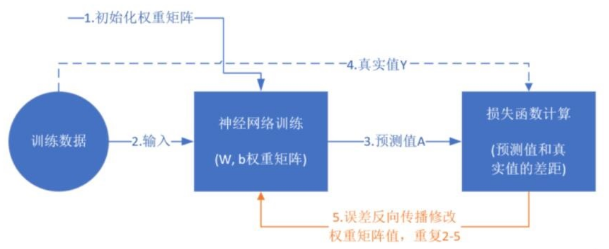
訓(xùn)練過程示意圖

04神經(jīng)網(wǎng)絡(luò)相關(guān)的概念

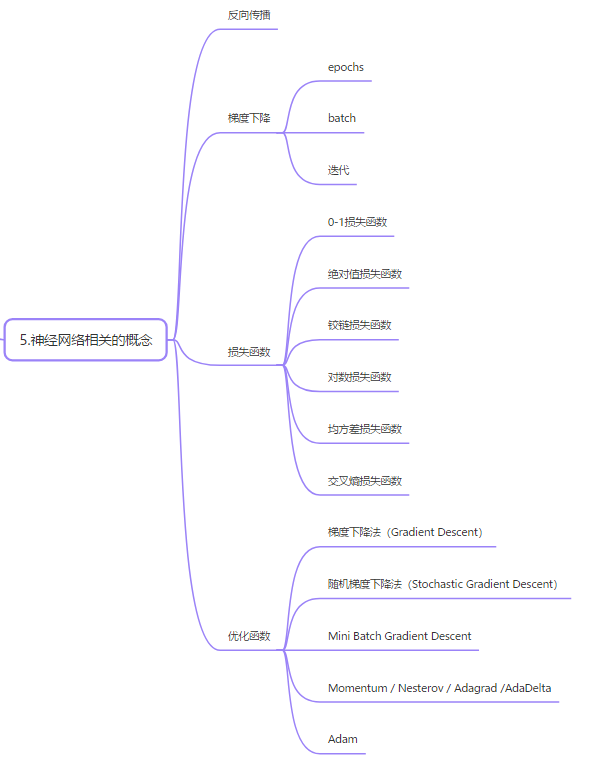
4.1反向傳播

反向傳播算法是一種高效計算數(shù)據(jù)流圖中梯度的技術(shù)，每一層的導(dǎo)數(shù)都是后一層的導(dǎo)數(shù)與前一層輸出之積，這正是鏈?zhǔn)椒▌t的奇妙之處，誤差反向傳播算法利用的正是這一特點(diǎn)。

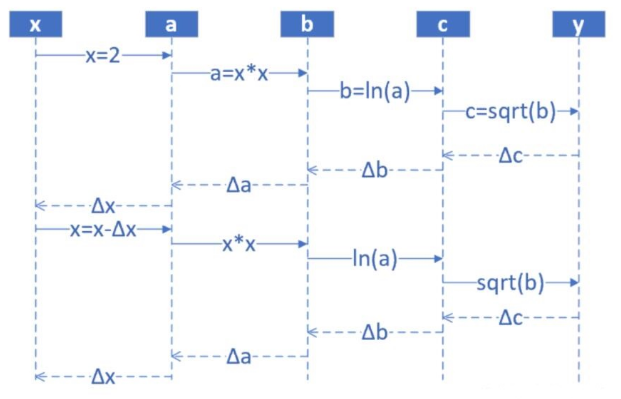
反向傳播算法示意圖

前饋時，從輸入開始，逐一計算每個隱含層的輸出，直到輸出層。

正向過程

step1，輸入層，隨機(jī)輸入第一個 x值，x 的取值范圍 (1,10]，假設(shè)x是 2；

step2，第一層網(wǎng)絡(luò)計算，接收step1傳入 x 的值，計算：a=x^2；

step3，第二層網(wǎng)絡(luò)計算，接收step2傳入 a 的值，計算：b=ln (a)；

step4，第三層網(wǎng)絡(luò)計算，接收step3傳入 b 的值，計算：c=sqrt{b}；

step5，輸出層，接收step4傳入 c 的值

然后開始計算導(dǎo)數(shù)，并從輸出層經(jīng)各隱含層逐一反向傳播。為了減少計算量，還需對所有已完成計算的元素進(jìn)行復(fù)用。

反向過程

反向傳播 --- 每一層的導(dǎo)數(shù)都是后一層的導(dǎo)數(shù)與前一層輸出之積

step6，計算y與c的差值：Δc = c-y,傳回step4

step7，step4 接收step5傳回的Δc，計算Δb = Δc*2sqrt(b)

step8，step3 接收step4傳回的Δb，計算Δa = Δb*a

step9，step2 接收step3傳回的Δa，計算Δx = Δ/(2*x)

step10，step1 接收step2傳回的Δx，更新x(x-Δx),回到step1,從輸入層開始下一輪循環(huán)

4.2.梯度下降

梯度下降是一個在機(jī)器學(xué)習(xí)中用于尋找最佳結(jié)果（曲線的最小值）的迭代優(yōu)化算法，它包含了如下2層含義：

梯度：函數(shù)當(dāng)前位置的最快上升點(diǎn)；

下降：與倒數(shù)相反的方向，用數(shù)學(xué)語言描述的就是那個減號，亦即與上升相反的方向運(yùn)動，就是下降，代價函數(shù)減小。

梯度下降數(shù)學(xué)公式

其中：

θ(n+1)：下一個值

θ(n):當(dāng)前值

-：減號，梯度的反向，

η：學(xué)習(xí)率或步長，控制每一步走的距離，不要太快，避免錯過了極值點(diǎn)；也不要太慢，以免收斂時間過長

▽：梯度 ，函數(shù)當(dāng)前位置的最快上升點(diǎn)

J(θ):函數(shù)

梯度下降算法是迭代的，意思是需要多次使用算法獲取結(jié)果，以得到最優(yōu)化結(jié)果。梯度下降的迭代性質(zhì)能使欠擬合的圖示演化以獲得對數(shù)據(jù)的最佳擬合。

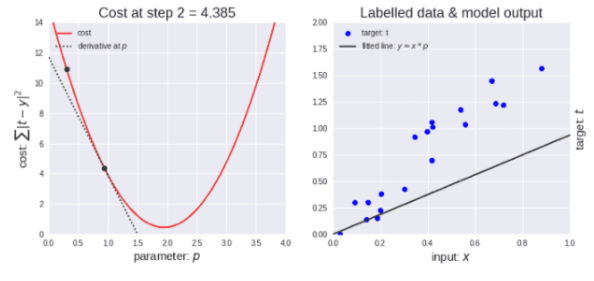
梯度下降算法示意圖

如上圖左所示，剛開始學(xué)習(xí)率很大，因此下降步長更大。隨著點(diǎn)下降，學(xué)習(xí)率變得越來越小，從而下降步長也變小。同時，代價函數(shù)也在減小，或者說代價在減小，有時候也稱為損失函數(shù)或者損失，兩者都是一樣的。

在一般情況下，一次性將數(shù)據(jù)輸入計算機(jī)是不可能的。因此，為了解決這個問題，我們需要把數(shù)據(jù)分成小塊，一塊一塊地傳遞給計算機(jī)，在每一步的末端更新神經(jīng)網(wǎng)絡(luò)的權(quán)重，擬合給定的數(shù)據(jù)。這樣就需要了解?epochs，batch size?這些概念。

epochs

當(dāng)一個完整的數(shù)據(jù)集通過了神經(jīng)網(wǎng)絡(luò)一次并且返回了一次，這個過程稱為一個?epoch。然而，當(dāng)一個?epoch?對于計算機(jī)而言太龐大的時候，就需要把它分成多個小塊。

設(shè)置epoch 的個數(shù)

完整的數(shù)據(jù)集在同樣的神經(jīng)網(wǎng)絡(luò)中傳遞多次。但是請記住，我們使用的是有限的數(shù)據(jù)集，并且我們使用一個迭代過程即梯度下降，優(yōu)化學(xué)習(xí)過程和圖示。因此僅僅更新權(quán)重一次或者說使用一個 epoch 是不夠的。

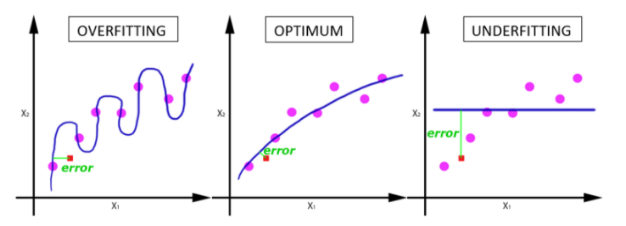
在神經(jīng)網(wǎng)絡(luò)中傳遞完整的數(shù)據(jù)集一次是不夠的，而且我們需要將隨著 epoch 數(shù)量增加，神經(jīng)網(wǎng)絡(luò)中的權(quán)重的更新次數(shù)也增加，曲線從欠擬合變得過擬合。那么，幾個 epoch 才是合適的呢？呵呵，這個問題并沒有確定的標(biāo)準(zhǔn)答案，需要開發(fā)者根據(jù)數(shù)據(jù)集的特性和個人經(jīng)驗(yàn)來設(shè)置。

batch

在不能將數(shù)據(jù)一次性通過神經(jīng)網(wǎng)絡(luò)的時候，就需要將數(shù)據(jù)集分成幾個?batch。

迭代

迭代是?batch?需要完成一個 epoch 的次數(shù)。記住：在一個 epoch 中，batch 數(shù)和迭代數(shù)是相等的。

比如對于一個有 2000 個訓(xùn)練樣本的數(shù)據(jù)集。將 2000 個樣本分成大小為 400 的 batch（5個batch），那么完成一個 epoch 需要 5次迭代。

4.3 損失函數(shù)

“損失”就是所有樣本的“誤差”的總和，亦即（mm 為樣本數(shù)）：

損失函數(shù)表達(dá)式

（1）0-1損失函數(shù)

（2）絕對值損失函數(shù)

（3）鉸鏈損失函數(shù)

（4）對數(shù)損失函數(shù)

（5）均方差損失函數(shù)

（6）交叉熵?fù)p失函數(shù)

均方差和交叉熵表達(dá)式

4.優(yōu)化函數(shù)

實(shí)例中的第1.4節(jié)，給創(chuàng)建的模型加入優(yōu)化器和損失函數(shù)

?

# 優(yōu)化器adam，線性回歸模型損失函數(shù)為均方差（mse）
model.compile(optimizer="adam",loss="mse")

?

這里使用的是adam優(yōu)化器，在神經(jīng)網(wǎng)絡(luò)中，優(yōu)化方法還有很多，這里選擇幾種做個簡單介紹，詳細(xì)信息還需要單獨(dú)去查找資料。

1)梯度下降法（Gradient Descent）

梯度下降法是最重要的一種方法，也是很多其他優(yōu)化算法的基礎(chǔ)。

2)隨機(jī)梯度下降法（Stochastic Gradient Descent）

每次只用一個樣本進(jìn)行更新，計算量小，更新頻率高；容易導(dǎo)致模型超調(diào)不穩(wěn)定，收斂也不穩(wěn)定

3)Mini Batch Gradient Descent

mini batch 梯度下降法是梯度下降法和隨機(jī)梯度下降法的折衷，即在計算loss的時候，既不是直接計算整個數(shù)據(jù)集的loss，也不是只計算一個樣本的loss，而是計算一個batch的loss，batch的大小自己設(shè)定。

4)Momentum

帶momentum(動量)的梯度下降法也是一種很常用的的優(yōu)化算法。這種方法因?yàn)橐肓薽omentum量，所以能夠?qū)μ荻认陆捣ㄆ鸬郊铀俚淖饔谩?/p>

5)Nesterov

NAG算法簡而言之，就是在進(jìn)行Momentum梯度下降法之前，先做一個預(yù)演，看看沿著以前的方向進(jìn)行更新是否合適，不合適就立馬調(diào)整方向。也就是說參數(shù)更新的方向不再是當(dāng)前的梯度方向，而是參數(shù)未來所要去的真正方向。

6)Adagrad

在訓(xùn)練過程中，每個不參數(shù)都有自己的學(xué)習(xí)率，并且這個學(xué)習(xí)率會根據(jù)自己以前的梯度平方和而進(jìn)行衰減。

優(yōu)點(diǎn)：在訓(xùn)練的過程中不用人為地調(diào)整學(xué)習(xí)率，一般設(shè)置好默認(rèn)的初始學(xué)習(xí)率就行了

缺點(diǎn)：隨著迭代的進(jìn)行，公式（6）中的學(xué)習(xí)率部分會因?yàn)榉帜钢饾u變大而變得越來越小，在訓(xùn)練后期模型幾乎不再更新參數(shù)。

7)AdaDelta

AdaDelta是Adagrad的改進(jìn)版，目的就是解決Adagrad在訓(xùn)練的后期，學(xué)習(xí)率變得非常小，降低模型收斂速度。

8)Adam

這里重點(diǎn)介紹一下Adam

前面我們從最經(jīng)典的梯度下降法開始，介紹了幾個改進(jìn)版的梯度下降法。

Momentum方法通過添加動量，提高收斂速度；

Nesterov方法在進(jìn)行當(dāng)前更新前，先進(jìn)行一次預(yù)演，從而找到一個更加適合當(dāng)前情況的梯度方向和幅度；

Adagrad讓不同的參數(shù)擁有不同的學(xué)習(xí)率，并且通過引入梯度的平方和作為衰減項(xiàng)，而在訓(xùn)練過程中自動降低學(xué)習(xí)率；

AdaDelta則對Adagrad進(jìn)行改進(jìn)，讓模型在訓(xùn)練后期也能夠有較為適合的學(xué)習(xí)率。

既然不同的參數(shù)可以有不同的學(xué)習(xí)率，那么不同的參數(shù)是不是也可以有不同的Momentum呢？

Adam方法就是根據(jù)上述思想而提出的，對于每個參數(shù)，其不僅僅有自己的學(xué)習(xí)率，還有自己的Momentum量，這樣在訓(xùn)練的過程中，每個參數(shù)的更新都更加具有獨(dú)立性，提升了模型訓(xùn)練速度和訓(xùn)練的穩(wěn)定性。

Adam（Adaptive Moment Estimation）：

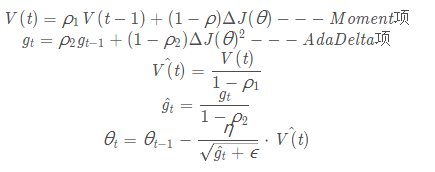
一般的，ρ 1 設(shè)置為0.9， ρ 2 設(shè)置為0.999

套用別人說過的一句話：

Adam works well in practice and outperforms other Adaptive techniques.

事實(shí)上，如果你的數(shù)據(jù)比較稀疏，那么像SGD，NAG以及Momentum的方法往往會表現(xiàn)得比較差，這是因?yàn)閷τ谀Ｐ椭械牟煌瑓?shù)，他們均使用相同的學(xué)習(xí)率，這會導(dǎo)致那些應(yīng)該更新快的參數(shù)更新的慢，而應(yīng)該更新慢的有時候又會因?yàn)閿?shù)據(jù)的原因的變得快。因此，對于稀疏的數(shù)據(jù)更應(yīng)該使用Adaptive方法（Adagrad、AdaDelta、Adam）。同樣，對于一些深度神經(jīng)網(wǎng)絡(luò)或者非常復(fù)雜的神經(jīng)網(wǎng)絡(luò)，使用Adam或者其他的自適應(yīng)（Adaptive）的方法也能夠更快的收斂。

05總結(jié)

回顧一下本文的主要內(nèi)容：

1）理解概念：人工神經(jīng)網(wǎng)絡(luò)靈感來自于生物神經(jīng)網(wǎng)絡(luò)，它可以通過增加隱層神經(jīng)元的數(shù)量，按照任意給定的精度近似任何連續(xù)函數(shù)來提升模型近似的精度。

2）實(shí)例介紹了構(gòu)建人工神經(jīng)網(wǎng)絡(luò)模型的機(jī)器學(xué)習(xí)實(shí)現(xiàn)過程

3）人工神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程

4）詳細(xì)介紹了神經(jīng)網(wǎng)絡(luò)相關(guān)的一些基本概念：反向傳播，梯度下降，損失函數(shù)，優(yōu)化函數(shù)，epoch,batch size ,優(yōu)化器，學(xué)習(xí)率等

審核編輯：湯梓紅