在人工智能蓬勃發展的今天，想了解它的原理似乎不是一件容易的事兒。其實它的核心問題仍然是數學，而且并不復雜，會比你想象的簡單得多。如果你登過山（在山間迷路更佳），那么你就能理解它的底層策略。

如何解釋人工智能的定義及其工作原理呢？我們只需要記住一點，它的基本原理就是數學，沒什么可怕的！? 現在，讓我們解釋一下機器學習的數學原理吧，因為這個“偉大的創意”比你想象的要簡單。

機器學習如登山

假設你不是一臺機器，而是一名登山者，正在努力地往山頂爬。但你沒帶地圖，四周又都是樹木和灌木叢，也沒有什么有利位置能讓你看到更廣闊的風景。那么，你該如何登頂呢？ 有一種策略是，評估你腳下的地面坡度。當你往北走的時候，地面坡度可能會略微上升，當你往南走的時候，地面坡度可能會略微下降。當你轉向東北方時，你發現那里有一個更陡峭的上坡。你在一個小圈里走來走去，勘察了你可能前往的所有方向，并發現其中一個方向的上坡是最陡峭的，于是你朝那個方向走了幾步。然后，你再畫一個圈，并從你可能前往的所有方向中選出最陡峭的上坡，以此類推。 現在，你知道機器學習的工作原理了吧！ 好吧，也許還不止這些，但這個叫作“梯度下降法”（Gradient descent）的概念是機器學習的核心。它其實是一種試錯法：你嘗試一堆可能的行動方案，然后從中選出最有助于你擺脫困境的那個。

與某個方向相關的“梯度”是一個數學概念，它是指“當你朝那個方向走一小步時，高度會發生多大的變化”，也就是你走的那條路的地面坡度。梯度下降法是一種算法，它利用數學語言制定了“一條明確的規則，告訴你在你可能遇到的各種情況下應該怎么做”。 這條規則是：考慮你可以朝哪些方向走，找出其中梯度最大的那個，并朝那個方向走幾步；重復上述步驟。 把你前往山頂的路線繪制到地形圖上，大致的樣子如圖1所示。

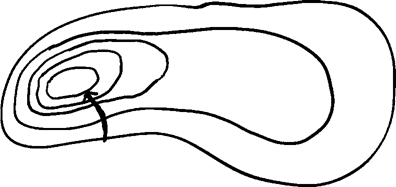
圖1 這又是一個很棒的幾何圖形。當你利用梯度下降法來指引方向時，你在地形圖上的路線必定與等高線垂直。

但它與機器學習又有什么關系呢？ 假設我不是一名登山者，而是一臺嘗試學些東西的計算機，例如阿爾法圍棋或GPT-3（能生成一長串看似合理且令人不安的英語文本的人工智能語言模型）。但一開始，先假設我是一臺嘗試學習貓是什么的計算機。 我該怎么做？答案是：采取類似于嬰兒的學習方法。在嬰兒生活的世界里，經常有大人指著他們視野中的某個東西說“貓”。你也可以對計算機進行這樣的訓練：給它提供1000幅貓的圖片，這些貓的姿態、亮度和情緒各不相同。

你告訴計算機：“所有這些都是貓。”事實上，如果你真想讓這種方法行之有效，就要另外輸入1000幅非貓的圖片，并告訴計算機哪些是貓而哪些不是。 機器的任務是制定一個策略，使它能夠自行區分哪些是貓而哪些不是。它在所有可能的策略之間徘徊，試圖找到最好的那個，即識別貓的準確度達到最高。它是個準登山者，所以它可以利用梯度下降法確定行進路線。你選擇了某個策略，將自己置于對應的環境中，然后在梯度下降規則的指引下前行。想一想你對當前策略可以做出哪些小改變，找出能為你提供最大梯度的那個，并付諸行動；重復上述步驟。

貪婪是相當好的東西

這句話聽起來頗有道理，但隨后你會發現自己并不明白它的意思。例如，什么是策略？它必須是計算機可以執行的東西，而這意味著它必須用數學語言來表達。對計算機而言，一幅圖片就是一長串數字。如果這幅圖片是600×600像素的網格，那么每個像素都有一個亮度，它們的值在 0（純黑）到 1（純白）之間。只要知道這 36 萬（600×600）個數字，就能知道這幅圖片是什么內容了。（或者，至少知道它的黑白圖像是什么樣子。） 策略是一種將輸入計算機的 36 萬個數字轉變成“貓”或“非貓”（用計算機語言來說就是“1”或“0”）的方法。用數學術語來表達的話，策略就是一個函數。事實上，為了更貼近心理現實，策略的輸出可能是一個介于 0 和 1 之間的數，它代表了當輸入是一幅模糊的猞猁或加菲貓枕頭圖片時，機器可能想表達的不確定性。當輸出是 0.8 時，我們應該將其解讀為“我幾乎可以肯定這是一只貓，但仍心存疑慮”。 例如，你的策略可能是這樣一個函數：“輸出你輸入的 36 萬個數字的平均值”。如果圖片是全白的，函數給出的結果就是 1 ；如果圖片是全黑的，函數給出的結果就是 0。

總的來說，這個函數可以測量計算機屏幕上圖片的總體平均亮度。這跟圖片是不是貓有什么關系？毫無關系，我可沒說它是一個好策略。 我們如何衡量一個策略是否成功呢？最簡單的方法是，看看那臺已學習過2000幅貓和非貓圖片的計算機接下來的表現。對于每幅圖片，我們都可以給策略打一個“錯誤分數”【現實世界中的計算機科學家通常稱之為“損失”（error or loss）】。如果圖片是貓且策略的輸出是 1，那么錯誤分數為0，也就是說答案正確。如果圖片是貓而策略的輸出是0，那么錯誤分數為 1，這是最壞的一種可能。如果圖片是貓而策略的輸出是0.8，那么答案近似正確但帶有些許不確定性，錯誤分數為0.2。（衡量錯誤程度的方法有很多種，這里說的并不是實踐中最常用的那種，但它更易于描述。） 把用于訓練的所有2000幅圖片的錯誤分數加總，就會得到總錯誤分數，它可以衡量你的策略是否成功。你的目標是找到一個總錯誤分數盡可能低的策略，怎樣才能讓策略不出錯呢？這就要用到梯度下降法了，因為現在你已經知道策略隨著你的調整而變得更好或更差意味著什么。

梯度測量的是，當你對策略稍做改變時錯誤分數的變化幅度；在你能對策略做出的所有小改變中，選出可使錯誤分數下降幅度最大的那個。梯度下降法不僅適用于貓，只要你想讓機器從經驗中習得策略，它就通通適用。 在這里，我不想低估計算方面的挑戰。那臺學習識別貓的計算機更有可能用數百萬幅圖片來訓練自己，而不只是2000幅。這樣一來，計算總錯誤分數時可能就需要加總100萬個錯誤分數。即使你擁有一臺強大的處理器，也需要花不少時間！所以在實踐中，我們經常使用梯度下降法的變體之一——隨機梯度下降法（Stochastic gradient descent）。這種方法涉及數不清的微小變化和錯誤分數，但它的基本理念是：第一步，你從大量的訓練圖片中隨機選擇一幅（比如，一只安哥拉貓或一個魚缸的圖片），然后采取可使這幅圖片的錯誤分數降至最低的那個步驟，而不是把所有的錯誤分數加在一起。

第二步，再隨機選擇一幅圖片，重復上述做法。隨著時間的推移（因為這個過程要進行很多步），最終所有圖片可能都會被考慮到。 我喜歡隨機梯度下降法的原因在于，它聽上去很瘋狂。例如，想象一下，美國總統正在制定全球戰略，一群下屬圍在他身邊大喊大叫，建議總統以符合他們自身特殊利益的方式調整政策。總統每天隨機選擇一個人，聽取他的建議，并對政策做出相應的改變。用這種方法管理一個大國是極其荒謬的，但它在機器學習方面卻行之有效！ 到目前為止，我們的描述缺失了一個重要因素：你如何知道何時該停止呢？你也許會說，很簡單啊，當我們做出任何小改變都不能使錯誤分數降低時，就可以停止了。但有一個大問題：你可能并未真正“登頂”！ 如果你是圖2中那個快樂的登山者，向左走一步或向右走一步，你會看到這兩個方向都不是上坡。這就是你快樂的原因：你自認為已經登頂了！

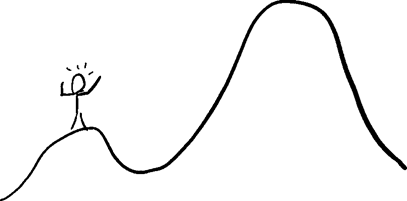
圖2 但事實并非如此。真正的峰頂還很遙遠，而梯度下降法不能幫你到達那里。你掉進了數學家所說的“局部最優值”（local optimum，局部極大值或局部極小值，它取決于你的目標是沖頂還是觸底。）陷阱，在這個位置上，任何小變化都不能產生改善效果，但它遠非真正的最佳站位。 我喜歡把局部最優值看作拖延癥的數學模型。假設你必須面對一項令人厭煩的任務，例如，整理一大摞資料，其中大部分與你多年來一直想達成的目標有關，扔掉它們則代表你最終選擇妥協，不打算繼續堅持下去了。每一天，梯度下降法都會建議你采取某個小行動，從而最大程度地提升你當天的幸福感。整理那一大摞資料會讓你感到快樂嗎？不，恰恰相反，它讓你感覺很糟糕。

推遲一天完成這項任務是梯度下降法對你的要求，第二天、第三天、第四天……算法每天都會給你同樣的建議。就這樣，你掉進了局部最優值——低谷——的陷阱，要想登上更高的山峰，你必須咬牙穿過山谷，那也許是很長的一段路，而且你得先往下走再往上爬。梯度下降法也被稱為“貪婪的算法”，因為它每時每刻都會選擇能使短期利益最大化的步驟。貪婪是罪惡之樹上的主要果實之一，但有一個關于資本主義的流行說法稱“貪婪是好東西”（greed is good）。在機器學習領域，更準確的說法是：“貪婪是相當好的東西。”梯度下降法可能會導致你陷入局部最優值陷阱，但相較于理論層面，這種情況在實踐中發生的次數并不多。 想繞過局部最優值，你需要做的就是暫時收起你的貪婪。所有好的規則都有例外。例如，在你登頂后，你可以不停下腳步，而是隨機選擇另一個地點，重啟梯度下降法。

如果每次的終點都是同一個地方，你就會更加確信它是最佳地點。在圖2 中，如果登山者從一個隨機地點開始使用梯度下降法，他就更有可能登上那座大山峰，而不是困在那座小山峰上。 在現實生活中，你很難將自己重置于一個完全隨機的人生位置上。更加切實可行的做法是，從你當前的位置隨機邁出一大步，而不是貪婪地選擇一小步。這種做法通常足以把你推到一個全新的位置上，向著人生巔峰邁進。 我是對還是錯？

還有一個大問題。我們愉快地決定考慮所有可能的小改變，看看其中哪一個能帶來最優梯度。如果你是一名登山者，擺在你面前的就是一個明確的問題：你在一個二維空間中選擇下一步的行動方向，這相當于在指南針上的一圈方向中擇其一，而你的目標是找出具有最優梯度的那個點。 但事實上，給貓圖片評分的所有可能策略構成了一個十分巨大的無限維空間。沒有任何方法能將你的所有選擇考慮在內，如果你站在人的角度而不是機器的角度，就會發現這一點顯而易見。假設我正在寫一本關于梯度下降法的自助類書籍，并且告訴你：“想要改變你的人生，做法很簡單。仔細考慮有可能改變你人生的所有方法，然后從中選擇效果最好的那個，這樣就可以了。”你看完這句話肯定會呆若木雞，因為所有可能改變你人生的方法構成的空間太大了，根本無法窮盡搜索。

如果通過某種非凡的內省法，你可以搜遍這個無限維空間呢？那樣的話，你還會碰到另一個問題，因為下面這個策略絕對可以使你的過往人生經歷的錯誤分數降至最低。 策略：如果你將要做的決策和你以前做的某個決策完全相同，就把你現在考慮的這個決策視為正確的決定。否則的話，拋硬幣決定吧。 如果換成學習識別貓的那臺計算機，上述策略就會變成： 策略：對于在訓練中被識別為貓的圖片，輸出“貓”。對于被識別為非貓的圖片，輸出“非貓”。對于其他圖片，拋硬幣決定吧。 這個策略的錯誤分數為0！對于訓練中使用的所有圖片，這臺計算機都會給出正確的答案。但如果我展示一幅它從未見過的貓圖片，它就會拋硬幣決定。如果有一幅圖片我展示過并告訴它那是貓，但在我把這幅圖片旋轉 0.01 度后，它也會拋硬幣決定。如果我向它展示一幅電冰箱的圖片，它還是會拋硬幣決定。它所能做的只是精確地辨識出我展示過的有限的貓和非貓圖片，這不是學習，而是記憶。 我們已經看到了策略失效的兩種方式，從某種意義上說它們是兩個極端。

1. 在你遇到過的許多情況下，這種策略都是錯的。

2. 這種策略只適用于你遇到過的情況，但對于新情況它一無是處。 前一個問題叫作“欠擬合”（Underfitting），是指你在制定策略時沒有充分利用你的經驗。后一個問題叫作“過擬合”（Overfitting），是指你太過依賴自己的經驗。我們如何在這兩個無用的極端策略之間找到一個折中的策略呢？答案是：讓這個問題變得更像登山。登山者搜索的是一個非常有限的選擇空間，我們也可以這樣，前提條件是我們要對自己的選擇加以限制。 我們本能地知道這一點。

在思考如何評估自己的人生策略時，我們通常使用的比喻是在地球表面選擇方向，而不是在無限維空間中隨機游走。美國詩人羅伯特·弗羅斯特將其比作“兩條分岔路”。傳聲頭樂隊（Talking Heads）的歌曲《一生一次》（Once in a Lifetime）猶如弗羅斯特的詩《未選擇的路》（The Road Not Taken）的續作，你仔細品讀就會發現，這首歌描繪的正是梯度下降法： 你可能會問自己那條公路通向哪里？你可能會問自己我是對還是錯？你可能會對自己說天啊！我到底做了什么？ 你不必把自己的選擇局限于一個旋鈕。 而線性回歸是選擇旋鈕的最常用方法之一。當統計學家尋找可根據一個已知變量的值預測另一個變量的策略時，線性回歸也是他們的首選工具。例如，一個吝嗇的棒球隊老板可能想知道，球隊的勝率對比賽門票的銷量會產生多大的影響。他不想在球場上投入太多的人力物力，除非它們能有效地轉化成上座率。

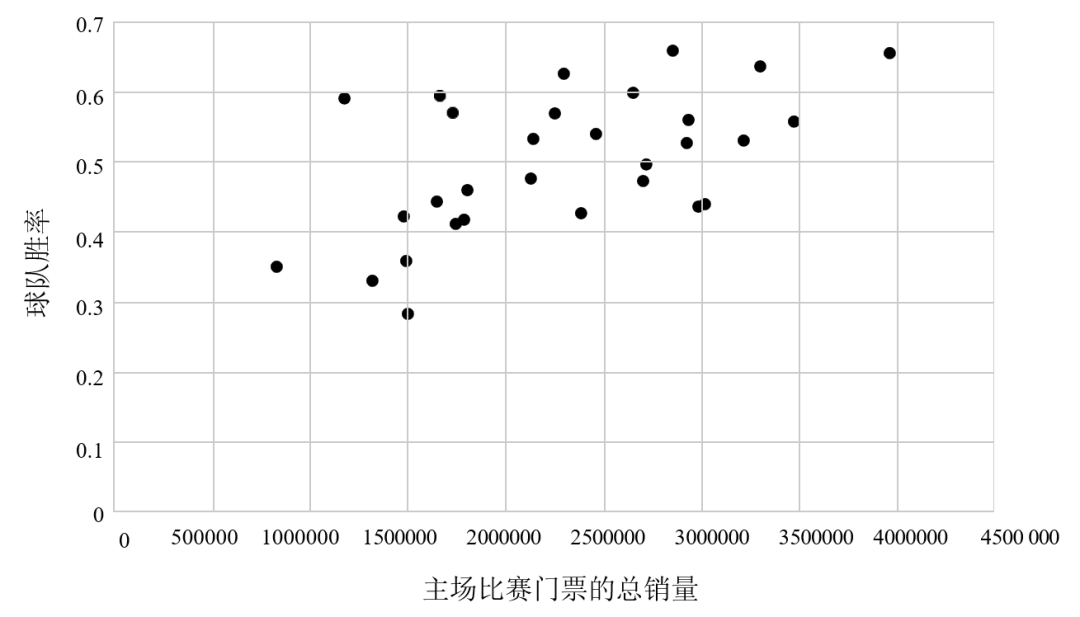
圖3 美國職業棒球大聯盟2019賽季的主場上座人數 vs 球隊勝率 圖3上的每個點分別代表一支球隊，縱坐標表示這些球隊在 2019 賽季的勝率，橫坐標表示這些球隊的主場上座人數。你的目標是找到一個能根據球隊勝率預測主場上座人數的策略，你允許自己考慮的選擇空間很小，而且其中的策略都是線性的。 主場上座人數 = 神秘數字 1 × 球隊勝率 + 神秘數字 2 任意一個類似的策略都對應著圖中的一條直線，你希望這條線能盡可能地匹配你的數據點。兩個神秘數字就是兩個旋鈕，你可以通過上下轉動旋鈕實現梯度下降，直到你無法通過任何微調降低策略的總體錯誤分數。（在這里，效果最佳的錯誤分數是所有球隊的線性策略預測值與真實值之差的平方和，所以這個方法通常被稱為“最小二乘法”。最小二乘法歷史悠久，發展至今已十分完善，用它來尋找最優直線的速度比梯度下降法快得多，但梯度下降法仍行之有效。） 最終，你會得到一條如圖4所示的直線。

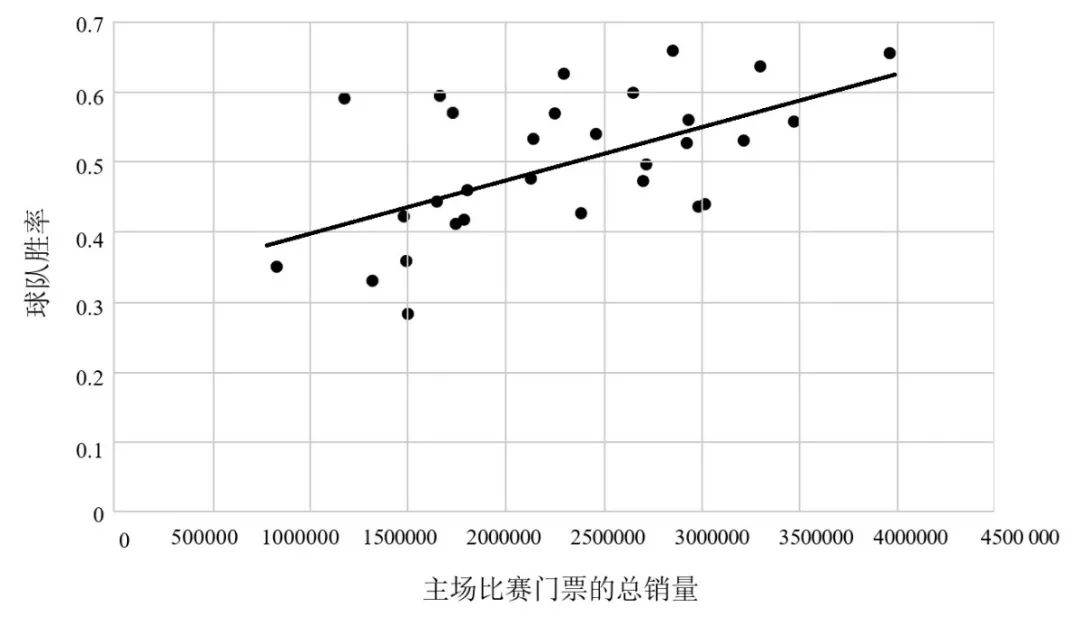
圖4 你可能會注意到，即使是錯誤分數最低的直線，其誤差也不小。這是因為，現實世界中的大多數關系都不是嚴格意義上的線性關系。我們可以試著納入更多的變量（比如，球隊體育場的大小應該是一個相關變量）作為輸入來解決這個問題，但線性策略的最終效果仍然有限。例如，這個策略不能告訴你哪些圖片是貓。在這種情況下，你不得不冒險進入非線性的狂野世界。 深度學習和神經網絡

在機器學習領域，正在研發的一種最重要的技術叫作“深度學習”。它有時以一種先知的姿態出現在人類面前，自動地、大規模地提供非凡的洞見。這種技術還有一個名稱——“神經網絡”，就好像這種方法能以某種方式自行捕獲人類大腦的運行方式一樣。 但事實并非如此。正如開頭所說，它的原理只是數學，甚至不是最新的數學。這一基本概念早在20世紀50年代末就出現了。而早在 1985 年使用一臺合成器就可以彈奏出鋼琴、小號和小提琴的音色，還可以用它制作你想要的音色，前提是你能掌握那本 70 頁說明書的晦澀內容，其中包含了很多如圖5所示的圖片。

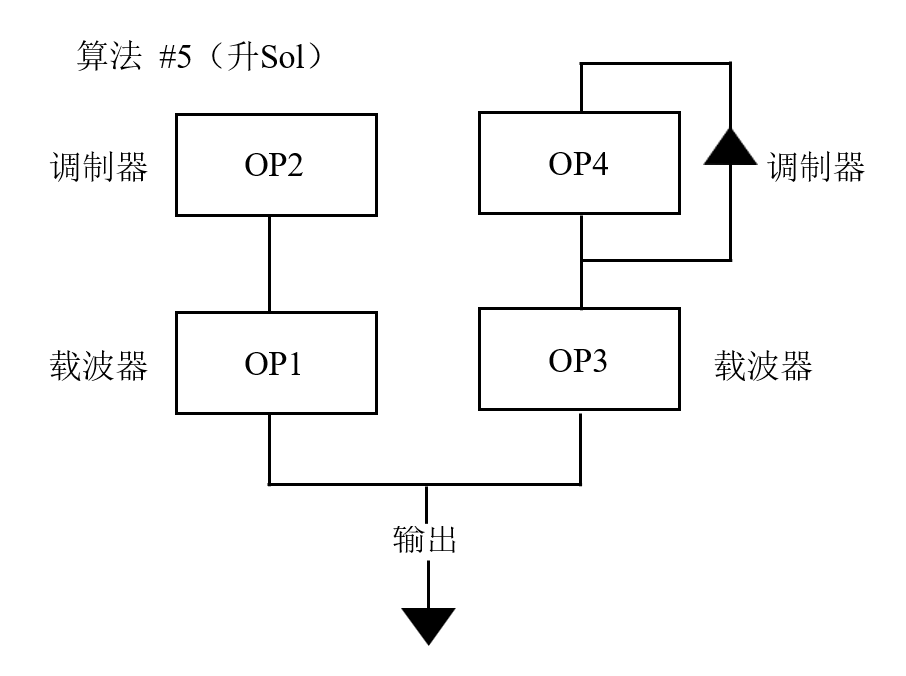
圖5 每個“OP”盒子代表一個合成器波，你可以通過轉動盒子上的旋鈕，讓聲音變得更響亮、更柔和、隨時間淡出或淡入，等等。這些都稀松平常，而DX21 真正神奇的地方在于它和操作者之間的連接。圖 5 展示了一個魯布·戈德堡機械式的過程，從OP1 發出的合成器波不僅取決于這個盒子上你可以轉動的那些旋鈕，還取決于OP2 的輸出。合成器波甚至可以自行調節，附屬于OP4 的“反饋”箭頭代表的就是這種功能。通過轉動每個盒子上的幾個旋鈕，你可以獲得范圍極其廣泛的輸出。這給了我嘗試的機會，自己動手制作新的音色。 神經網絡跟合成器很像，它是由幾個小盒子構成的網絡，如圖6所示。

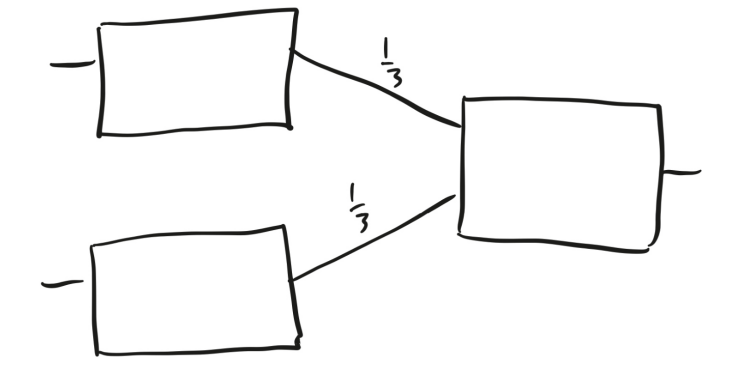
圖6 所有盒子的功能都相同：如果輸入一個大于或等于 0.5 的數字，它們就會輸出1；否則，它們就會輸出 0。用這種盒子作為機器學習基本元素的想法，是在1957—1958 年由心理學家弗蘭克·羅森布拉特（Frank Rosenblatt）提出來的，他視其為神經元工作原理的一個簡單模型。盒子靜靜地待在那里，一旦接收到的刺激超過某個閾值，它就會發射一個信號。羅森布拉特把這類機器稱作“感知機”（Perceptrons）。為了紀念這段歷史，我們仍然稱這些假神經元網絡為“神經網絡”，盡管大多數人不再認為它們是在模擬人類的大腦硬件。 數字一旦從盒子中輸出，就會沿著盒子右側的任意箭頭運動。每個箭頭上都有一個叫作“權重”的數字，當輸出沿箭頭呼嘯而過時，就會乘以相應的權重。每個盒子把從其左側進入的所有數字加總，并以此作為輸入。 每一列被稱為一層，圖6中的網絡有兩層，第一層有兩個盒子，第二層有一個盒子。你先向這個神經網絡輸入兩個數字，分別對應第一層的兩個盒子。以下是有可能發生的情況：

1. 兩個輸入都不小于 0.5。第一層的兩個盒子都輸出 1，當這兩個數字沿著箭頭移動時，都變為 1/3，所以第二層的盒子接收到 2/3 作為輸入，并輸出 1。

2. 一個輸入不小于 0.5，另一個輸入小于 0.5。那么，兩個輸出分別是 1 和 0，所以第二層的盒子接收到 1/3 作為輸入，并輸出 0。

3. 兩個輸入都小于 0.5。那么，第一層的兩個盒子都輸出 0，第二層的盒子也輸出 0。 換句話說，這個神經網絡是一臺機器，它接收到兩個數字作為輸入，并告訴你它們是否都大于0.5。 圖7是一個略顯復雜的神經網絡。

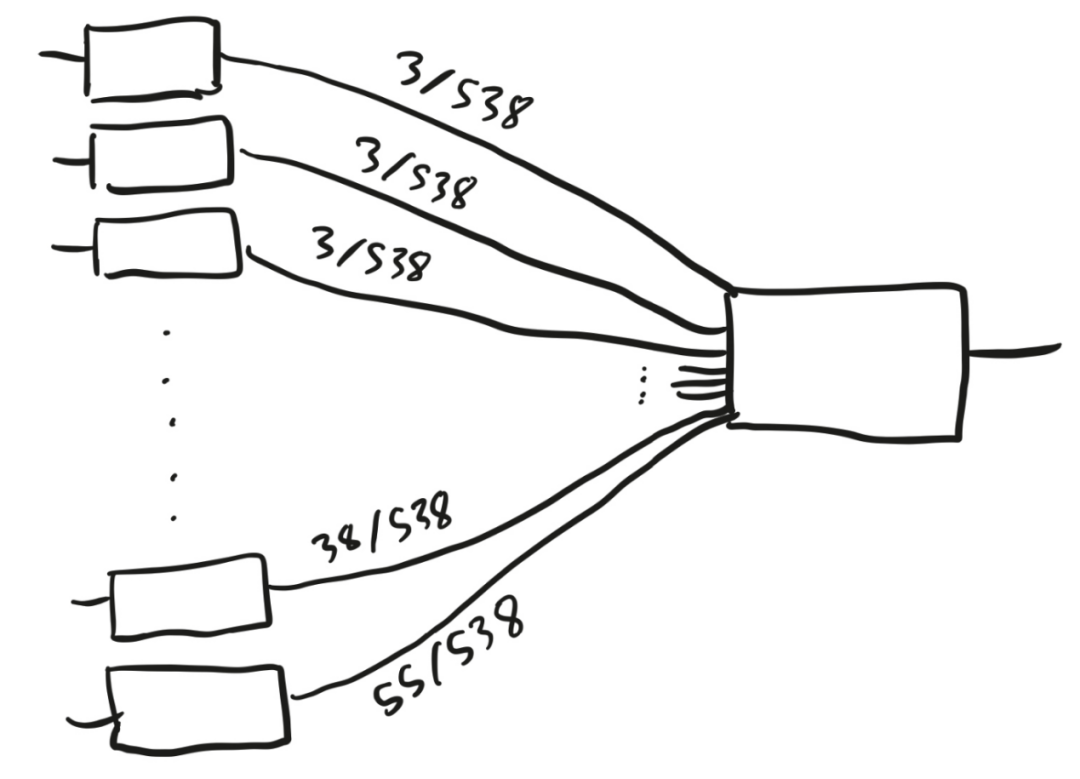
圖7 該神經網絡的第一層有51個盒子，它們都向第二層的那個盒子輸入數字。但箭頭上的權重不同，最小的權重為 3/538，最大的權重為55/538。這臺機器在做什么？它將51個不同的數字作為輸入，并激活每個輸入大于0.5的盒子。然后，它對這些盒子進行加權計算，檢驗它們的和是否大于0.5。如果是，就輸出1；如果不是，則輸出 0。 我們可以把它稱作“兩層羅森布拉特感知機”，但它還有一個更常用的名稱——“選舉人團制度”。51個盒子代表美國的50 個州和華盛頓特區，如果共和黨候選人在某個州獲勝，代表該州的盒子就會被激活。把所有這些州的選舉人票數加總后除以538，如果結果大于0.5，共和黨候選人就是贏家。 圖8是一個更現代的例子，它不像選舉人團制度那樣易于用語言來描述，但它與驅動機器學習不斷進步的神經網絡更加接近。

圖8 圖8中的盒子比羅森布拉特感知機的盒子更精致。盒子接收到一個數字作為輸入，并輸出該數字和0中較大的那個。換句話說，如果輸入是一個正數，盒子就會原封不動地輸出這個數字；但如果輸入是一個負數，盒子就會輸出 0。 我們來試試這個裝置（見圖9）。假設我先向最左邊一層的兩個盒子分別輸入1和1。這兩個數字都是正數，所以第一層的兩個盒子都會輸出 1。再來看第二層，第一個盒子接收到的數字是 1×1 = 1，第二個盒子接收到的數字是-1×1 = -1。同理，第二層的第三個盒子和第四個盒子接收到的數字分別是 1 和-1。1是正數，所以第一個盒子輸出1。但第二個盒子接收到的輸入是一個負數，未能被觸發，所以它輸出 0。同樣地，第三個盒子輸出1，第四個盒子輸出 0。

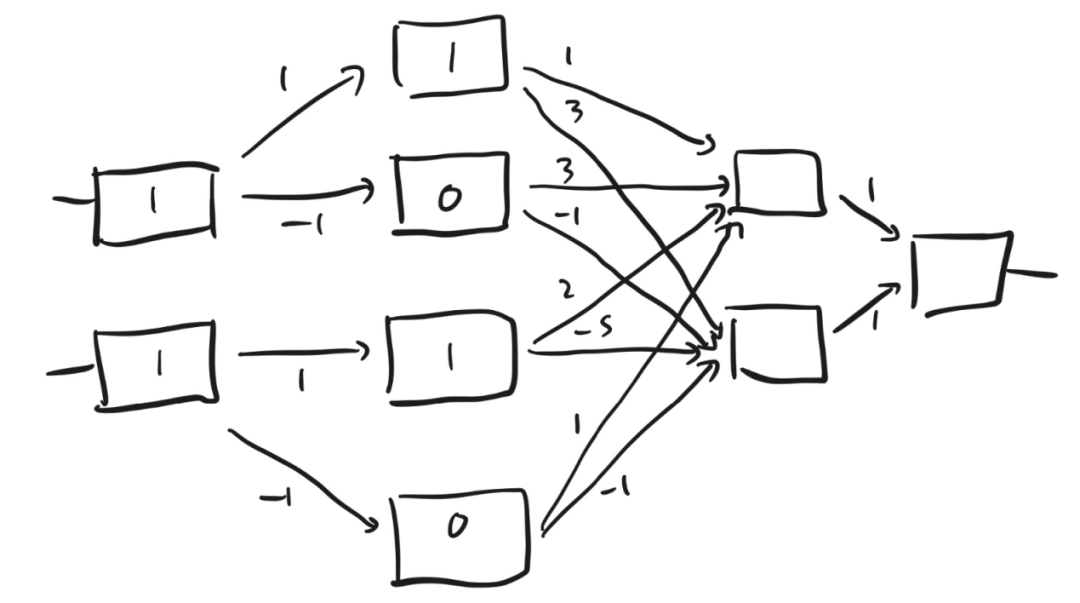
圖9 接著看第三層，上面的盒子接收到的數字是1×1+3×0+2×1+1×0=3，下面的盒子接收到的數字是3×1?1×0?5×1?1×0=?2。所以，上面的盒子輸出3，下面的盒子未能被觸發，輸出0。最后，第四層的那個盒子接收到的兩個輸入之和為1×3+1×0=3。 即使你未關注到這些細節，也沒有關系。重要的是，神經網絡是一個策略，它接收到兩個數字作為輸入，并返回一個數字作為輸出。如果你改變箭頭上的權重，也就是說，如果你轉動14個旋鈕，就會改變這個策略。圖9為你提供了一個十四維空間，讓你根據既有的數據從中找出最適合的策略。如果你覺得很難想象出十四維空間的樣子，我建議你聽從現代神經網絡理論的創始人之一杰弗里·辛頓（Geoffrey Hinton）的建議：“想象一個三維空間，并大聲對自己說‘這是十四維空間’。所有人應該都能做到這一點。”辛頓來自一個高維空間愛好者家族，他的曾祖父查爾斯在1904年寫了一本關于如何想象四維立方體的書，并發明了“超立方體”（tesseract）一詞來描述它們。不知道你有沒有看過西班牙畫家薩爾瓦多·達利的油畫作品《受難》，其中就有一個辛頓的超立方體。 圖10中這個神經網絡的權重已知，如果平面上的點（x， y）位于灰色形狀內部，就賦予它一個等于或小于3的值。注意，當點（1， 1）位于灰色形狀的邊界上時，策略賦予它的值是3。

圖10 不同的權重會產生不同的形狀，雖然不是任意形狀。感知機的本質意味著這個形狀永遠是多邊形，即邊界由多條線段構成的形狀。（前文中不是說這應該是非線性的嗎？沒錯，但感知器是分段線性（piecewise linear）結構，這意味著它在空間的不同區域內滿足不同的線性關系。更通用的神經網絡可以產生更彎曲的結果。） 如圖11所示，假設我用X 標記了平面上的一些點，用O 標記了其他一些點。我給機器設定的目標是讓它習得一個策略：根據我標記的那些點，用X 或O為平面上其他未標記的點賦值。也許（希望如此）我可以通過正確設置那 14 個旋鈕得到某個策略，將較大的值賦予所有標記為X 的點，而將較小的值賦予所有標記為O 的點，以便我對平面上尚未標記的點做出有根據的猜測。

如果真有這樣的策略，我希望可以通過梯度下降法來習得它：微微轉動每個旋鈕，看看這個策略在給定例子中的錯誤分數會降低多少，從中找出效果最佳的那個操作，并付諸實施；重復上述步驟。深度學習中的“深度”僅指神經網絡有很多層。每層的盒子個數被稱為“寬度”（width），在實踐中，這個量可能也很大。但相比“深度學習”，“寬度學習”少了一些專業術語的味道。 可以肯定的是，今天的深度學習網絡比上文中的那些示意圖要復雜得多，盒子里的函數也比我們討論過的簡單函數要復雜得多。

遞歸神經網絡中還包含反饋盒子，就像 合成器上的“OP4”一樣，把自身的輸出作為輸入。而且，它們的速度明顯更快。正如我們所見，神經網絡的概念已經存在很長時間了，我記得就在不久前，人們還認為這條路根本走不通。但事實證明，這是一個很好的想法，只不過硬件必須跟上概念的步伐。為快速渲染游戲畫面而設計的GPU芯片，后來被證明是快速訓練大型神經網絡的理想工具，有助于實驗人員提升神經網絡的深度和寬度。

有了現代處理器，你就不必再受限于 14 個旋鈕，而可以操控幾千、幾百萬乃至更多的旋鈕。GPT-3 生成的英語文本能以假亂真，它使用的神經網絡有1750億個旋鈕。 有1750億個維度的空間聽起來的確很大，但和無窮大相比，這個數量又顯得微不足道。同樣地，與所有可能的策略構成的空間相比，我們正在探索的只是其中很小的一部分。但在實踐中，這似乎足以生成看起來像人類創作的文本，就好比合成器的小型網絡足以模擬出小號、大提琴和太空霹靂的音色。 這已經非常令人驚訝了，但還有一個更深層次的謎。記住，梯度下降法的理念就是不斷轉動旋鈕，直到神經網絡能在訓練過的數據點上取得盡可能好的效果。今天的神經網絡有許許多多旋鈕，所以它們常能做到在訓練集上表現完美，把 1000 幅貓圖片中的每一幅都識別為“貓”，而把1000 幅其他圖片全部識別為“非貓”。 事實上，有這么多的旋鈕可以轉動，讓訓練數據百分之百正確的所有可能策略就會構成一個巨大的空間。事實證明，當神經網絡面對它從未見過的圖片時，這些策略中的大多數都表現得很糟糕。但是，蠢笨又貪婪的梯度下降過程出現在某些策略中的頻率通常高于其他策略，而在實踐中，梯度下降法偏愛的那些策略似乎更容易推廣到新的例子中。

為什么呢？是什么使得這種特殊形式的神經網絡擅長應對各種各樣的學習問題？我們在策略空間中搜索的這塊微不足道的區域，為什么恰恰就包含了一個好的策略呢？ 據我所知，它是一個謎。坦白地說，關于它是不是一個謎的問題，還存在很多爭議。我向很多聲名顯赫的人工智能研究者提問過這個問題，他們回答起來個個口若懸河。其中一些人非常自信地解釋了其中的原因，但每個人的說法都不一樣。

撰文 | 喬丹·艾倫伯格（Jordan Ellenberg）翻譯 | 胡小銳、鐘毅

編輯：黃飛