來源:混沌巡洋艦
作者:人工智能學家
為什么說人臉識別是一種明知識?
促使人們意識到暗知識和人工智能的關系的,首先是有學習能力的神經網絡在擴大科學經驗方面的運用,它明確無誤地把暗知識和某一種裝置對應起來。也許,人臉識別是最簡單的例子。自古以來,人臉識別是(科學)經驗知識,而且是一種明晰的經驗知識。為什么說人臉識別是一種(科學)經驗的明知識?所謂人臉識別實為主體看到某一圖像,即可根據該圖像把某人從人群(或記憶)中找出來。這里,看到圖像為獲得可靠信息,它是一個普遍可重復的受控觀察。把某人從人群(或記憶)中找出為完成某種選擇(控制),其為主體對可控制變量的控制。人臉識別作為科學的經驗知識,實為獲得信息和實現某種控制之間的確定聯系。通常,主體是知曉識別過程的(這種聯系如何建立),即它屬于科學經驗知識中的明知識。當人臉識別可用其他方式做到,即用一個有學習能力的人造神經網絡來識別人臉時,主體并不知道神經網絡是如何做到的,人臉識別也就成為暗知識。
今天,人臉識別裝置已在社會生活中得到廣泛運用。人臉識別是主體基于經驗的一種能力,當這種能力用某種機器實現時,該機器就是有智能的。我們已經看到,當某一種暗知識是用某一種人造裝置獲得時,該裝置一定對應著一種獲得相應知識的智能。在很多人心目中,和人臉識別這種近于本能的簡單能力相比,下棋才真正體現出主體擁有的高級智能。然而,只要我們去分析下棋過程,就會發現它同樣是主體獲得(科學)經驗知識,只是獲得經驗知識的過程較為復雜而已!因為和人臉識別一樣,下棋同樣是主體根據獲得的信息(棋局)來實現某種控制(下一步選擇)。如果說人臉識別是信息和控制之間的一次性對應,下棋經驗就是主體獲得信息和實行控制之間對應關系構成的序列。每一次,主體根據棋局的信息做一次選擇,改變了棋局,然后根據對手改變的棋局再次選擇。這由一次次選擇構成的序列有自己的明確目標,那就是下棋每一步的結果規定的最后結果。
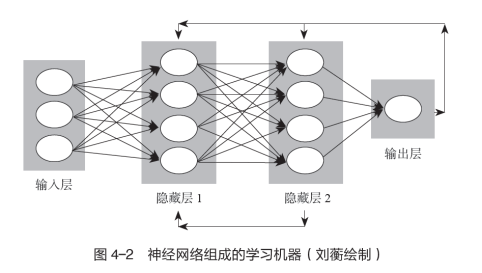
既然下棋的知識實為每一次獲得信息后如何進行選擇,那么每一次獲得信息規定選擇什么,是一種(科學)經驗知識,它和人臉識別一樣,是可以通過一個人造神經網絡的學習訓練實現的。由于選擇序列冗長,兩次選擇互相依賴,下棋的輸贏取決于該序列最后的結果,這一切使人造神經網絡的結構和學習訓練方式比人臉識別復雜得多。但無論人造神經網絡的結構和學習訓練多么復雜,其整體上仍是圖4-2所示的學習機器。因此,在神經網絡組成的學習機器學會下棋后,主體如何下棋亦成為暗知識。和這種暗知識直接對應的是下棋的能力,由此我們可以理解為什么神經網絡組成的學習機器戰勝世界圍棋冠軍那么重要了,因為這是人工智能登上歷史舞臺的象征。
2016年3月9日舉行了神經網絡學習機器AlphaGo(阿爾法圍棋)和世界圍棋冠軍、職業九段棋手李世石的公開比賽。只要有過下圍棋的經驗,就知道這種經驗知識有多復雜,掌握它無疑需要相當高的智能。AlphaGo具有應付千變萬化的圍棋棋局的智能嗎?人們是持懷疑態度的。但這場比賽的結果是AlphaGo以4∶1取勝,這是有史以來第一次世界圍棋冠軍輸給了神經網絡學習機器。這場比賽不僅意味著神經網絡學習機器戰勝人,而且意味著人無法理解AlphaGo如何下棋。機器的下棋方式是名副其實的暗知識。暗知識和智能的關系終于被世人意識到了。事實不正是如此嗎?暗知識這個觀念正是王維嘉為了說明神經網絡機器是如何用一種和人類獲得經驗知識完全不同的方式時提出的。從此以后,科學界普遍認識到,只要主體明確要獲得的經驗知識是什么,都可以用神經網絡學習機器來取代人,即神經網絡學習機器可以運用到獲得科學經驗知識的任何一個領域。
地圖四色定理證明中的爭議
早在20世紀40年代神經網絡學習機器的數學模型剛提出時,它已經被證明是有限自動機,并和圖靈機等價,即它既可以用來表達電脈沖輸入與輸出互動中的學習,亦可用來計算和邏輯推理。因此,對科學知識的另一種類型——數學知識,只要用公理推出定理必須通過某種計算機裝置,就證明其中也存在暗知識。圖靈機就是通用電子計算器,通用電子計算器(馮·諾依曼機)的發明比神經網絡學習機器早,故在科學經驗知識中發現暗知識之前,人類已經知道數學中存在著暗知識。地圖四色定理的證明是典型的例子。
地圖四色定理由一個英國業余數學家弗朗西斯·格斯里在1852年提出,它是指任何一張地圖只用四種顏色就能使具有共同邊界的國家著上不同的顏色。地圖即平面圖,它由圖論的一組公理給出。這樣,證明地圖四色定理就是將其用平面圖的公理推出。證明這一猜想極為困難。1878年英國數學家阿爾弗雷德·肯普發現,如果地圖至少需要五色,則一定存在一種正規五色地圖。接著他證明:如果有一張正規的五色地圖,就會存在一張國數最少的極小正規五色地圖;如果極小正規五色地圖中有一個國家的鄰國數少于六個,就會存在一張國數比其還要少的正規五色地圖,這樣就不會有國數極小的五色地圖,也就不存在正規五色地圖了。通過歸謬法,肯普認為他已經證明了地圖四色定理。但若干年后,英國數學家約翰·赫伍德發現了肯普的證明存在漏洞。
肯普的證明雖被否定,但他提出的兩個概念對解決四色問題提供了方法。第一個概念是構形。肯普證明在每一張正規地圖中至少有一國具有兩個、三個、四個或五個鄰國,不存在每個國家都有六個或更多個鄰國的正規地圖。另一個概念是可約性,即只要五色地圖中有一國具有四個或五個鄰國,就會有國數減少的五色地圖。自從引入構形和可約的概念后,數學家逐步發展出一套檢查構形是否可約的標準方法。研究者發現,解決四色問題要證明構形可約,需要檢查大量的細節。1950年德國數學家海因里希·黑施通過不斷試驗指出,用構形化約證明四色定理,涉及的構形有一萬多種。要對如此多的構形逐一證明,工作量極為巨大,這非人力所能完成。正因如此,人們一度認為地圖四色定理是無法證明的。
1975年愚人節,美國數學家、數學科普作家馬丁·加德納在《科學美國人》上發布了一張地圖,聲稱四色猜想被否定,因為這張地圖需要至少五種顏色才能完成上色。當然,這只是一個玩笑。然而,人們萬萬沒有想到,就在幾個月以后,美國伊利諾伊大學的數學家沃夫岡·黑肯對黑施的方法做了改進,他與美國數學家肯尼斯·阿佩爾合作設計了一個計算機程序,在計算機專家科克的參與下,終于在1976年1月6日證明了四色猜想。他們是利用窮舉檢驗法檢查了1482種構形,一個又一個地證明它們都是可約的,即沒有一張需要五色。該工作是在兩臺IBM360計算器上各做了100億個判斷實現,計算機運行達1200多個小時,兩臺計算機得到一樣的結果。用計算機證明四色定理引起了轟動,但也帶來了巨大的爭議。
黑肯等人設計的構形化約程序當然是正確的,但化約和相應判斷是運用兩臺計算機分別做出的,鑒別其可靠與否的方法是看兩臺計算機得到的結果是否一致。這種做法有點像工程技術和物理學鑒定。這里,證明計算機工作是否可靠,就和判別用電子顯微鏡觀察對象所獲得的信息是否可靠一模一樣。美國數學家威廉·瑟斯頓曾評論說:“一個可以運作的計算機程序,其正確性和完備性標準比起數學界關于可靠的證明的標準,要高出幾個數量級。”但是,沒有人全面驗證過四色猜想證明的每一步,原因是人力不可能做到。正因如此,很多數學家不認可上述證明,蘇格蘭數學家弗蘭克·波塞爾指出,這種證明根本不屬于數學。
我認為,可以從兩個方面來梳理地圖四色定理證明中的爭議。一是有些人不知道數學知識中也有暗知識。地圖四色問題的證明,屬于抽象代數中純圖論的領域。圖論定理由相應的基本公理規定。規定這些公理時,已給出相應符號系統的所有可靠信息,證明定理只是把公理注入的信息找出來。主體獲得公理注入的可靠信息和主體經歷每一步信息的獲得過程,原則上亦可分離。數學知識中存在暗知識是沒有疑義的。然而,在人類所具有的數學知識中,暗知識占的比例很小,數學家還不習慣數學知識中的暗知識。然而,我要問:為什么一定存在著一個不同于現在已給出四色問題證明的非窮舉式證明呢?數學家遲早會意識到必須接受數學知識中亦存在暗知識。
此外,數學家不承認地圖四色問題被證明還有一個原因,那就是拒絕這種證明體現了人的數學能力。愛因斯坦做過一個比喻:純數學是邏輯思想的詩歌,但四色定理的確證依靠的是計算機對人不能處理的個案之窮舉,它猶如一本電話簿。數學家很難想象如查電話簿般的、用計算機的快速窮舉是一種數學智能。正因如此,至今這個領域的研究被稱為機器證明,而非人工智能。但是,任何一種暗知識都對應著一種智能,我們能否定這種幫助數學家獲得暗知識的裝置是人工智能嗎?答案是沒有疑義的。純數學是普遍可重復的受控實驗無限擴張的符號表達,主體在研究純符號系統的結構時,任何一種處理符號系統的能力當然也是智能。因此,在數學領域,由于計算機的運用,用人工智能獲得暗知識比在經驗領域要早,只是因為其稀少,沒有被意識到罷了。
人工智能的歷史
其實,只要去追溯人工智能的歷史,就知道人工智能正是在利用電子計算機處理符號結構時提出的。早在1956年,數十名來自數學、心理學、神經科學、計算機科學與電氣工程學領域的學者聚集在一起,討論如何用計算機來處理符號結構,會上美國計算機科學家約翰·麥卡錫將這種研究命名為人工智能;同樣作為計算機科學家的艾倫·紐厄爾和司馬賀把一種被稱為“邏輯理論家”的程序帶到會議上,他們被會議發起人稱為“人工智能之父”。縱觀這些被稱為人工智能的研究,無一不是發明一種處理信息(符號系統或數字)的裝置,用其來整理和提取解決問題的知識。無論是邏輯理論家,還是1959年司馬賀、紐厄爾和軟件工程師約翰·肖公布的通用問題求解系統,都是如此。這種裝置和前文講過的兩類裝置(具有學習能力的神經網絡和進行數學定理證明的計算機)的不同之處在于,前者處理的不是純科學經驗知識,亦不是純數學知識,而是科學理論知識。正因為人工智能一開始就被界定為如何用一種裝置實現運用科學理論知識解決實際問題,或通過經驗提出科學理論,其被廣泛地稱為專家系統。
舉個例子。1964年美國人工智能學家愛德華·費根鮑姆、分子生物學家喬舒亞·萊德伯格和化學家卡爾·杰拉西用某種裝置處理火星上采集來的數據,看火星上有無可能存在生命。三人合作的結果就是第一個專家系統DENDRAL的誕生。DENDRAL輸入的是質譜儀的數據,輸出的是給定物質的化學結構。另一個例子是1978—1983年司馬賀和計算機科學家帕特·蘭利、蓋里·布拉茨霍夫陸續發布了6個版本的BACON系統發現程序,該裝置重新發現了一系列著名的物理、化學定律。縱觀各式各樣的專家系統,它們都是在創造一種裝置,以獲得科學理論知識的信息。專家系統有時是用科學理論推出經驗知識,解決碰到的實際問題;有時是根據受控實驗信息提出科學理論,或修改現有的科學理論知識。這些工作本來都是由人完成的,而專家系統是一種人造裝置,用它來取代人做的事情。
我要問一個問題:這些專家系統獲得的可靠信息中有暗知識嗎?根據暗知識的定義,我們知道最后得到的可靠信息是什么,但不知道該信息是如何獲得的。今日所有已知的專家系統都沒有這樣的智能。專家系統之所以做不到這一點,是因為它們不能如人工神經網絡那樣自行學習,也不能如機器證明那樣完全不需要人的干預自行進行邏輯判斷。如前所述,科學理論知識的進步依靠的是科學理論信息和經驗信息的互動,它包括當從科學理論推出之受控實驗信息不包含相應科學經驗的受控實驗信息時,規定兩者哪一個必須修改,即兩者如何互動。只有互動過程形成完全的閉環(沒有主體參與),其才能完全通過人工裝置來實現。這時,主體通過該裝置得到科學理論的信息,但不知道該信息是如何得到的。這才是科學理論中的暗知識。
目前,這種裝置正在孕育之中,美國人工智能研究實驗室OpenAI推出的一款大型預訓練人工智能語言模型ChatGPT也許是一個例子。為什么?科學理論作為橫跨受控實驗和數學世界的拱橋,由拱圈和上蓋組成。上蓋是用邏輯語言表達的受控實驗和受控觀察,即目前文獻中記錄的科學知識。拱圈是建立在測量之上用數量表達的受控實驗(觀察)結果之間的關系,它是作為各門科學基礎的定律。ChatGPT利用自然語言的語法研究把自然語言陳述轉化為邏輯語言陳述,然后自動把這些邏輯語言陳述中所蘊含的信息提取出來。當人通過ChatGPT得到了新的科學理論知識,但不知道該新知識是如何得到的時,科學理論知識滿足暗知識的定義。對于拱圈,亦可以建立電腦控制的受控實驗和受控觀察,獲得測量數據和實現控制都不需要主體直接參與。這時,研究者也不知道得到的新定律是如何得到的。這也是科學理論的暗知識。
更重要的是,上蓋是建立在拱圈之上的。只要將從陳述中得到新信息和電腦自行做實驗結合,我們將發現,在科學理論中,暗知識的增長將超過明知識。在今日迅速發展的合成生物學中,正在醞釀著兩者結合的可能性。這意味著人工智能第三種形態(獲得科學理論知識中的暗知識的裝置)也許最先在生命科學中被使用,其背后是物理、化學、數學、信息理論與生命科學理論深度交叉,形成基因合成、基因編輯、蛋白質設計、細胞設計、實驗自動化的使能技術。其中,生命鑄造廠(biofoundry)或許是典型的例子。然而,在被稱為大設施的生命鑄造廠的建造和調試中,有中國研究者卻以“造物致知”作為口號。該口號沿用了中國傳統的“格物致知”,大設施的建造者或許沒有想到,只要合成生物學中有關設施實現了科學理論知識修改的閉環,科學理論知識中的暗知識就會產生。這種“致知”和我們熟悉的獲得知識不盡相同。通過造物大設施的運作,合成生物會源源不斷地被制造出來,但這一切不一定導致今日所知的那種生命科學理論知識的增長,因為它們中的相當一部分可能都是暗知識。
人類發現科學理論中存在大量暗知識,標志著自然現象因果解釋的一場革命。我們知道自然現象服從因果律,但能體驗因果律認識過程的只是知曉因果律的極小一部分。即便如此,也并不妨礙人類用因果性改造世界,因為就算大多數因果律是暗知識,我們仍可以通過人工智能來駕馭它們。
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App



















評論