作者：zjyspeed ?|?

A*算法

學習知識，有一個由淺入深的過程．研究圖搜索算法，離不開深度優先搜索 (Depth First Search, DFS) 和廣度優先搜索 (Breadth First Search, BFS),?大部分算法都是由最基礎的算法演變而來的．A* 算法的基石，就是廣度優先搜索 (BFS)。

本部分將從 BFS 開始介紹，看看算法是如何一步步進化到 A* 的。

廣度優先搜索(BFS)

廣度優先搜索，是算法里老生長談的話題了．無論是在數據結構面試題還是科研中，都具有舉足輕重的地位。

所謂廣度優先，也就是優先搜索距源點距離較近的點，如上圖所示，廣度優先的視覺效果為以源點為中心的擴散搜索．代碼如下：

?frontier表示當前的搜索邊界，也可以理解為用于下一步搜索的備用節點集合(如 gif 中的藍色方格)，在編程中通常用優先級隊列來表示

?came_from記載了從起點到當前點的途徑信息，回溯 came_from, 可以得到從起點到當前點的路徑

?while循環非常重要，這個循環框架是整個 A* 部分圖搜索算法的核心部分，大致分為如下幾步

按照既定規則，在當前的搜索邊界frontier中選取一個方格current作為下一步的搜索點(這個既定規則，就是區分 BFS, Dijkstra, A* …等等算法的關鍵所在)，在 BFS 中的規則是廣度優先，而frontier邊界中的點本來就是按遍歷順序排列的，直接選取隊列首元素

為了擴展方便，我們把這個既定規則，數學化表示成代價函數 f(n)，算法每次都會選取隊列中f(n) 最小的進行下一步擴展，廣度優先搜索的代價函數f(n) 其實就是節點加入隊列的順序，那么就不需要進行優先級比較了，隊列本來就是先入先出的。

擴展current，得到current的相鄰節點集合?neighbors, 放入備用節點集合frontier

Dijkstra

算法的研究，最終是要為應用服務的．在廣度優先算法中，我們以當前點距起點的距離作為遍歷的優先級．這樣的遍歷順序在普通場景下尚可，但在某些復雜場景下卻顯得力不從心，例如過橋和過河，對我們來說同樣的距離，過橋顯然輕松的多．為此，算法將引入代價?cost 作為新的代價函數f(n)=cost：

定義?cost: 從當前點?current?到起點的路徑所需要的代價 (根據 cost 定義的不同，又可以誕生其他的算法，比如下文將要介紹到的?Greedy Best First Search?和 A*)

每次選取代價最小的節點優先遍歷

代碼如下：

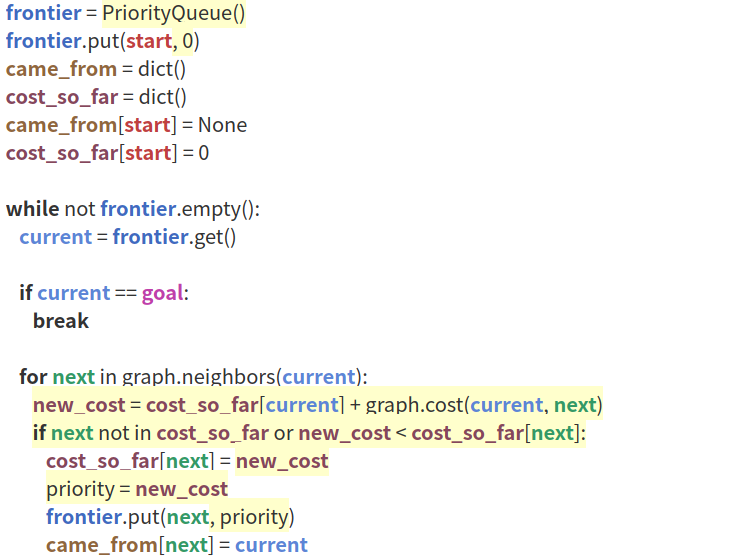
相比于 BFS，Dijkstra 算法新增了cost_so_far用于記錄從當前點current到起點的路徑所需要的代價，并將搜索規則改為優先搜索cost最小的點．如下圖所示，，Dijkstra 算法會繞過中央難走的草地．

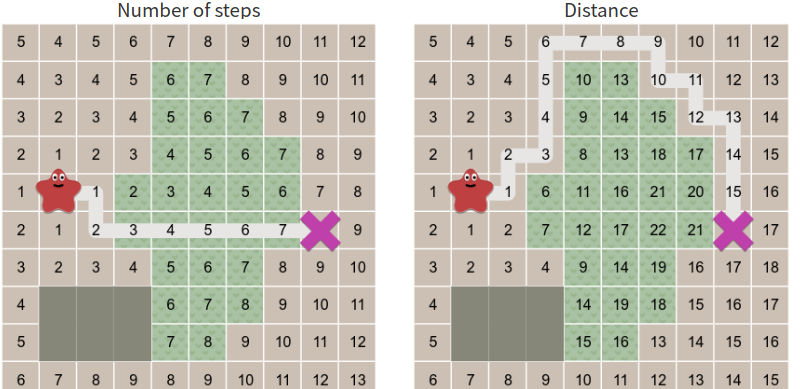
最佳優先搜索 Greedy Best First Search

在 BFS 和 Dijkstra 算法中，算法從起點開始向所有方向擴散遍歷，直到最外層的擴散圈覆蓋目標點. 這樣的搜索會同時計算出從起點到包括目標點在內的的大量點的最優路徑. 我們不禁思考這樣的搜索有沒有必要.

舉個例子，我們想去直線距離10km外的商場，需要找到最近的道路，我們難道會繞著起點一圈一圈擴大搜索直到找到商場嗎？這種搜索方法顯然是有悖常理的，正常人的做法是沿著朝向商場的方向搜索，如果路走不通，才有可能往反方向走來繞過障礙.

這樣沿著目標點方向的搜索，叫做啟發式搜索 (Heuristic search)，事實上，一切利用到目標點信息的搜索，都叫啟發式搜索. 啟發式搜索算法中，都有一個啟發式函數?(Heuristic function)，最簡單的啟發式函數就是當前搜索點current到目標點的距離：

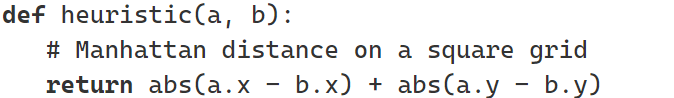
前文提到，while循環框架貫穿 A* 類搜索算法的始終，不一樣的只是確定下一個搜索點的既定規則， 也叫代價函數，也就是優先級隊列的比較規則，回顧一下：

?BFS 的規則:?順序優先f(n)= 加入隊列的順序(廣度優先)

?Dijkstra 的規則:?到起點的距離優先:f(n)=cost_so_far

可以看到，相比于啟發式搜索，BFS和Dijkstra沒有方向性，相應的，這類搜索通常也稱為盲目搜索.

在最佳優先搜索 (Greedy Best First Search) 中，?while循環框架中確定下一個搜索點的代價函數修改為啟發函數:f(n)=heuristic(n,goal)

如果使用當前搜索點current到目標點的距離(這里的距離是曼哈頓距離)為啟發函數，則最佳優先搜索的優先級隊列比較規則為到目標點的距離優先，代碼如下：

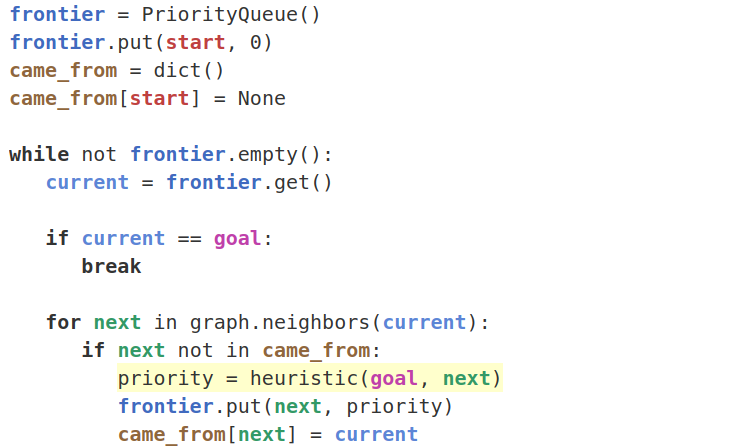
相比于 Dijkstra，最佳優先搜索直接朝著目標點方向行進：

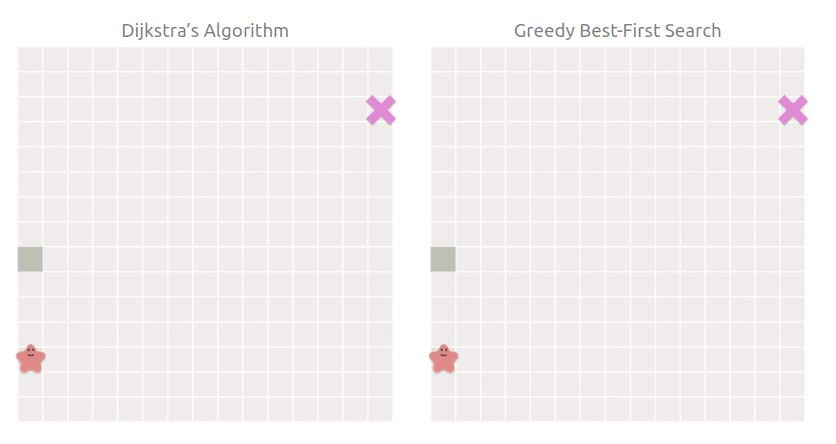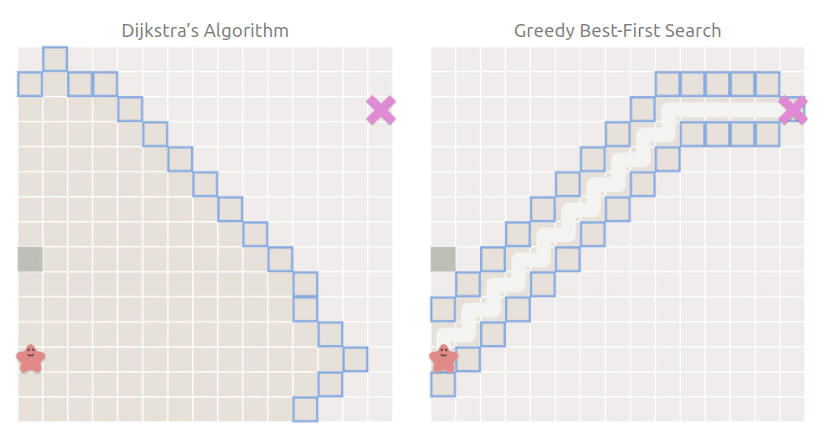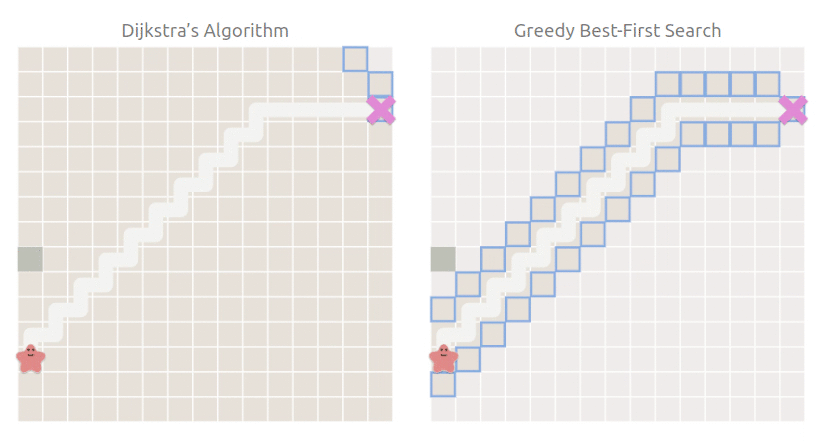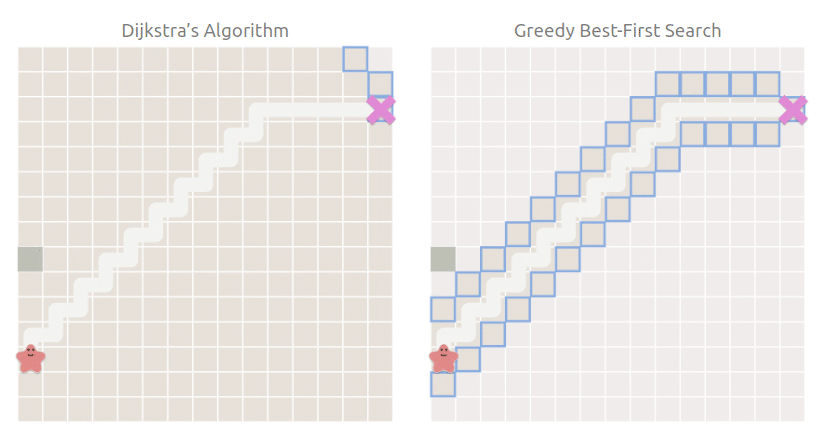
當然，現實的情況沒有這么理想，每一條路不可能都是坦途，如果有障礙物怎么辦呢：

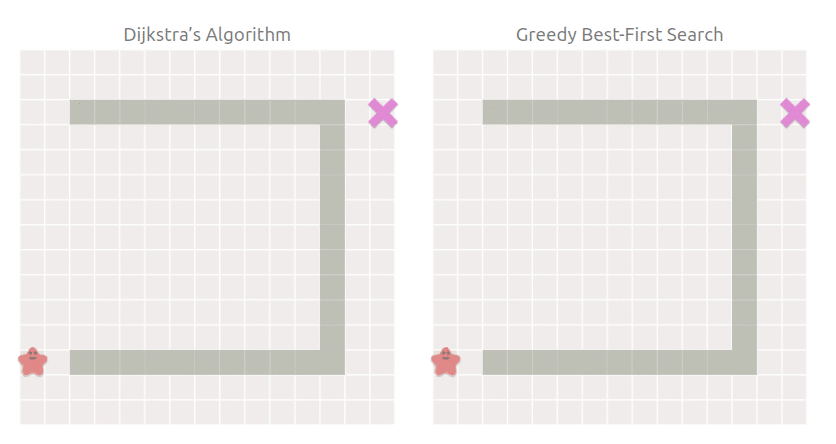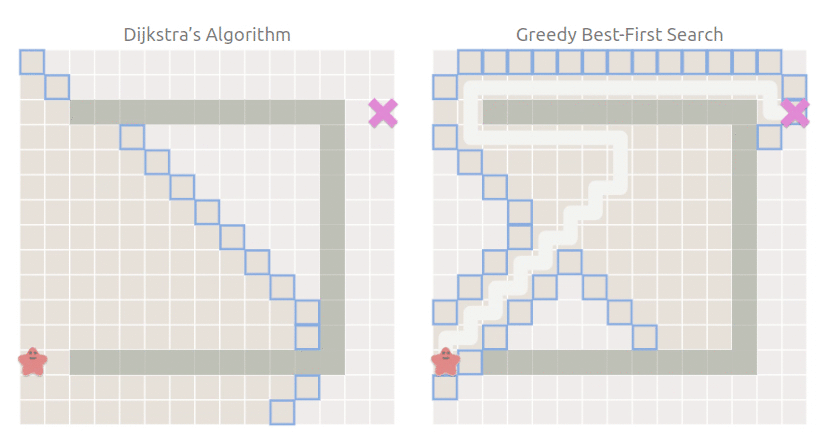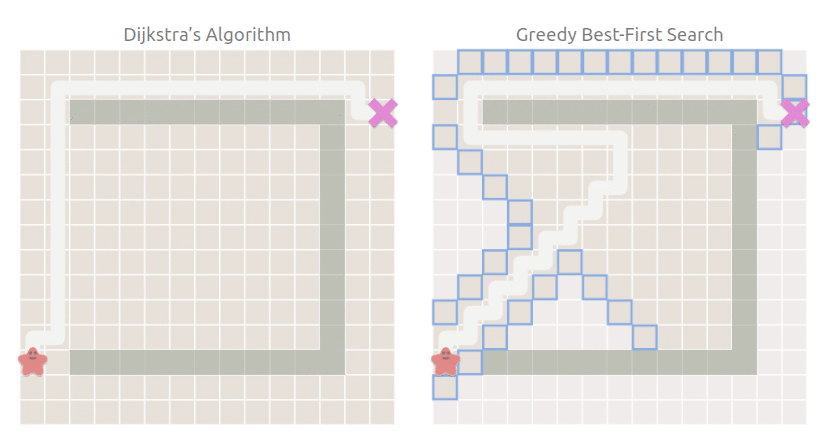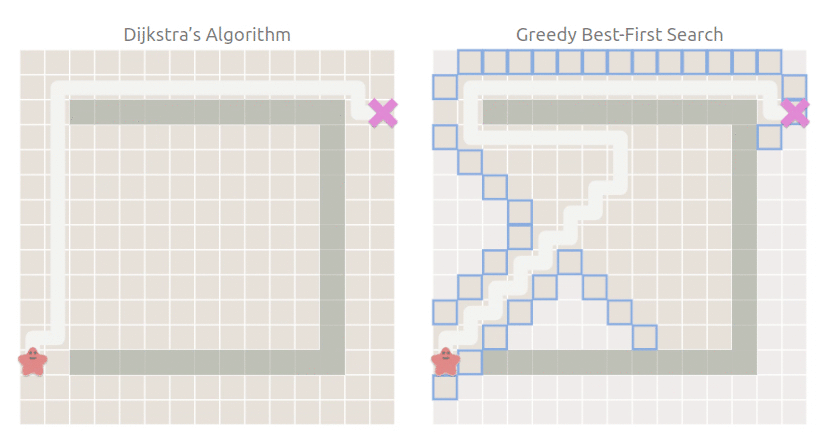
可以看到，最佳優先搜索仍然朝著目標點方向搜索，搜索空間雖然比 Dijkstra 小，但是走了彎路，也就是雖然搜索快，但是找到的路徑不是最短路徑.

那有沒有方法，幫助我們找到又快又短的路徑呢？

A*

受 Dijkstra 和 GBFS(Greedy Best First Search) 的啟發，A* 決定博采眾長.

?Dijkstra:?到起點的距離優先 ：f(n)=cost_so_far

?Greedy Best First Search：到目標點的距離優先?:f(n)=heuristic(n,goal)

?A*:到起點和目標點的距離之和優先：f(n)=cost_so_far+heuristic(n,goal)

代碼如下：

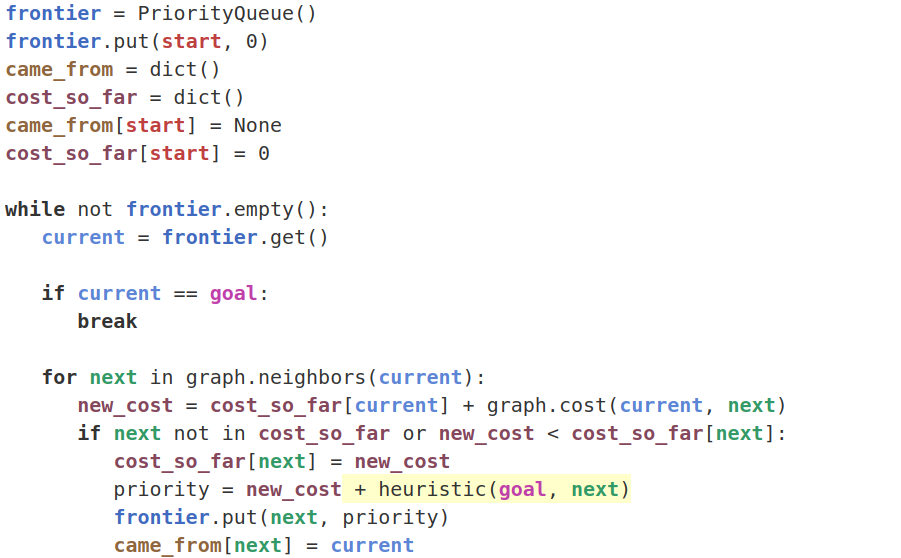
可以看到，博采眾長之后，在上述地圖，與 Dijkstra 相比， A* 算法能找到最短路徑，且搜索空間更小；與 GBFS 相比，A* 算法能找到最短路徑，但搜索空間更大.

到這里，就不得不提到算法最優性、完備性和效率之間的折衷了.

最優性：指規劃得到的路徑在某個評價指標上是最優的，例如經常使用的路徑長度指標，最短路徑即是最優路徑. 在上述算法中，Dijkstra 是最優的， 對A* 算法來說，只要啟發函數沒有低估到目標點的距離(稱為啟發函數的一致性(admissible))，A* 算法也是最優的.

完備性：如果在起點和目標點之間有解存在，算法一定能找到解. 在上述算法中，BFS、Dijkstra、A* 都是完備的，在有限狀態空間圖搜索中，最佳優先搜索 GBFS 也是完備的.

算法的效率取決于算法的平均搜索空間，用算法術語來說叫時間復雜度. 這里就不展開介紹了，上面的幾個 gif 展示的搜索過程，可以直觀的看到各個算法的搜索空間. 完備性、最優性與算法效率往往是矛盾的. 完備、最優注定了精益求精，更快的算法通常是次優的.?沒有最好的算法，只有最適合的算法.

以下介紹的 A* 變種算法的提出，大都由于最優性、完備性和效率之間的折衷。限于篇幅和博主能力，A* 變種算法只簡要的概括思想，具體內容可以閱讀每個算法給出的參考文獻。

為了便于下文介紹，我們需要對 A* 算法的術語描述進行一些修改：

上文提到，A* 算法的代價函數為:f(n)=cost_so_far+heuristic(n,goal) .

在這里需要簡化一下A* 算法的代價函數的表示方法，這也是大部分文獻中所采用的:f(n)=g(n)+h(n)

其中，g(n) 代表著當前點n到起點的距離，也就是上文的cost_so_far，h(n) 代表著啟發函數heuristic. 這里插一句題外話，規定h是因為h是heuristic的首字母，那么g代表著什么？答案是沒有什么，因為 A* 算法提出者在文章里就是這么規定的…

上文提到，frontier?表示當前的搜索邊界，也即為用于下一步搜索的備用節點集合，在一般的編程框架里，frontier通常被稱為open list，一般翻譯過來叫Open 表. 相應于open list，還有一個closed list，每次從open list 中取出的優先級最高的節點current 都會被放入closed list 中，表示該節點已經被探索過.

這里推薦一個非常好的網站，里面包括了很多圖搜索算法和采樣搜索算法的可視化搜索過程和編程實現:?https://github.com/zhm-real/PathPlanning，下文的 gif 示例大部分取自該網站.

Bidirectional A*（雙向A*）

雙向 A* 算法維護兩套 A* ，最精髓的思想在于從起點和終點分別、同時向對方搜索，但是雙向搜索過程中的處理邏輯有很多需要考慮的地方：例如是輪流搜索還是優先搜索起點開始的 A*？

一種可能的搜索過程如下:

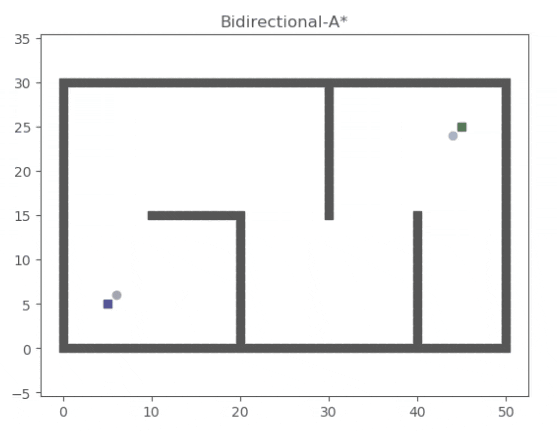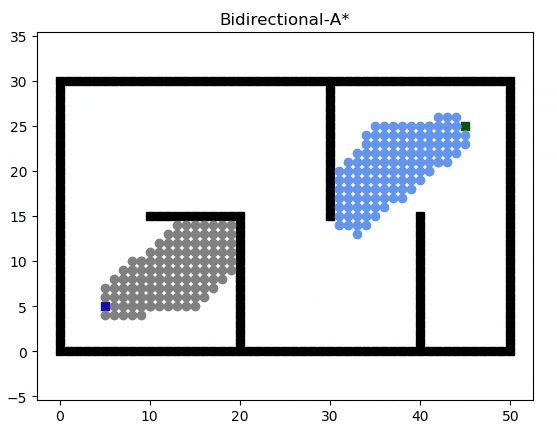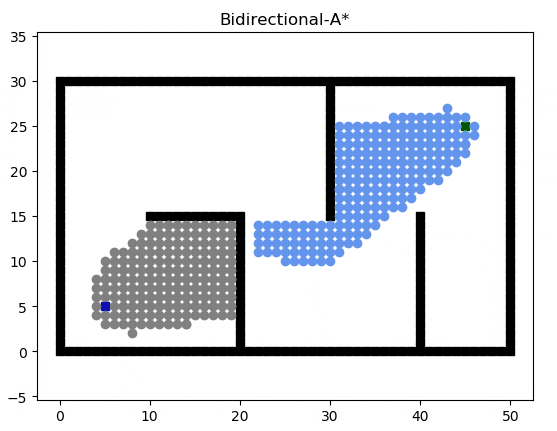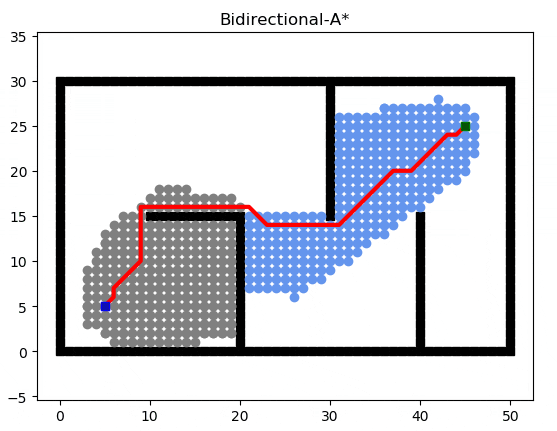
次優算法

Weighted A* （WA*）

回顧一下經典算法的代價函數：

A*:f(n)=g(n)+h(n)

Dijkstra:f(n)=g(n)

GBFS:f(n)=h(n)

Weighted A* 集思廣益，為了滿足用戶各種情景的需求，設計了一個權重因子 ω

f(n)=g(n)+ω×h(n)

觀察上述代價函數，發現：

?ω=0 時，Weighted A* 退化為 Dijkstra

?ω=1 時，Weighted A* 退化為 A*

?ω=∞ 時，Weighted A* 退化為 GBFS

在有限狀態空間圖搜索中，上述算法都是完備的，調整參數ω便是算法最優性與求解速度之間的折衷。

Anytime Repairing A* （ARA*）

參考文獻: ARA*: Anytime A* with Provable Bounds on Sub-Optimality（https://proceedings.neurips.cc/paper_files/paper/2003/file/ee8fe9093fbbb687bef15a38facc44d2-Paper.pdf）

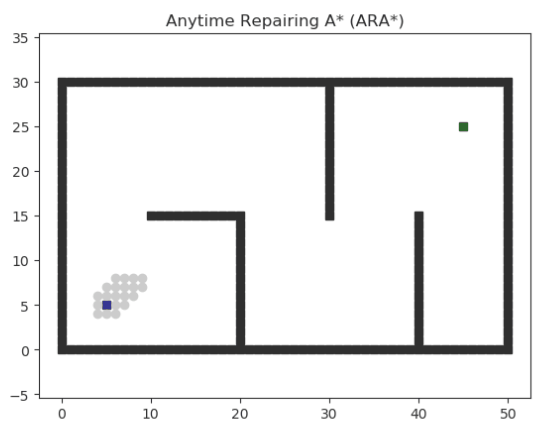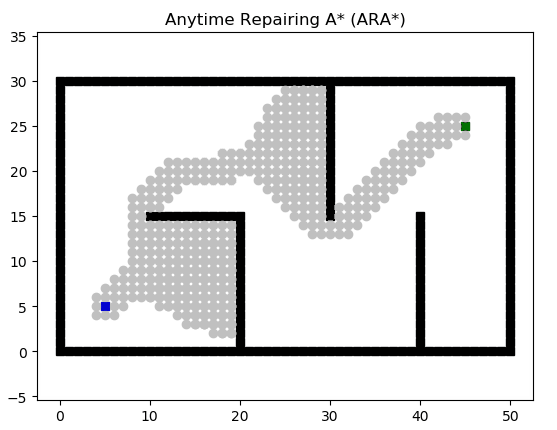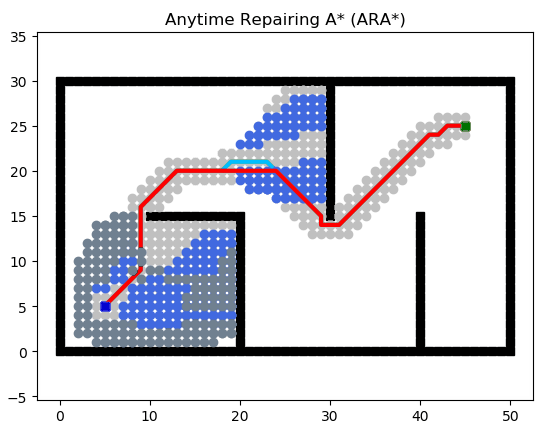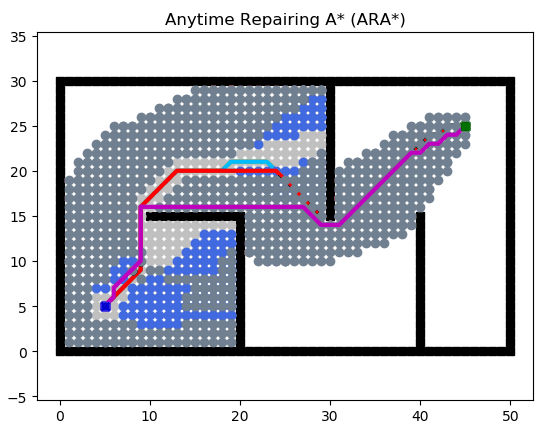
ARA* 做了兩件事情:

?快速找到一條可用的路徑

?用剩余時間對這條路徑進行優化

當然，這個邏輯的提出已經不是什么新鮮事情了，ARA* 的精髓在于 用剩余時間對這條路徑進行優化 這件事情是如何復用優化前的搜索路徑結果、大大降低計算量的。具體可以參考論文。

Focal Search （A ??）

參考文獻：Studies in Semi-Admissible Heuristics（https://ieeexplore.ieee.org/document/4767270）

這篇論文介紹了三種次優算法，這里簡要介紹其中最著名的 FOCAL Search，也叫A ??，這是一種有界次優算法。

?

動態搜索

動態搜索(Dynamic search)，也叫增量搜索(Incremental search)和長期規劃(Lifelong search)，可以在環境地圖改變時，基于先前路徑快速搜索出新的規劃路徑，而無需從頭開始搜索。

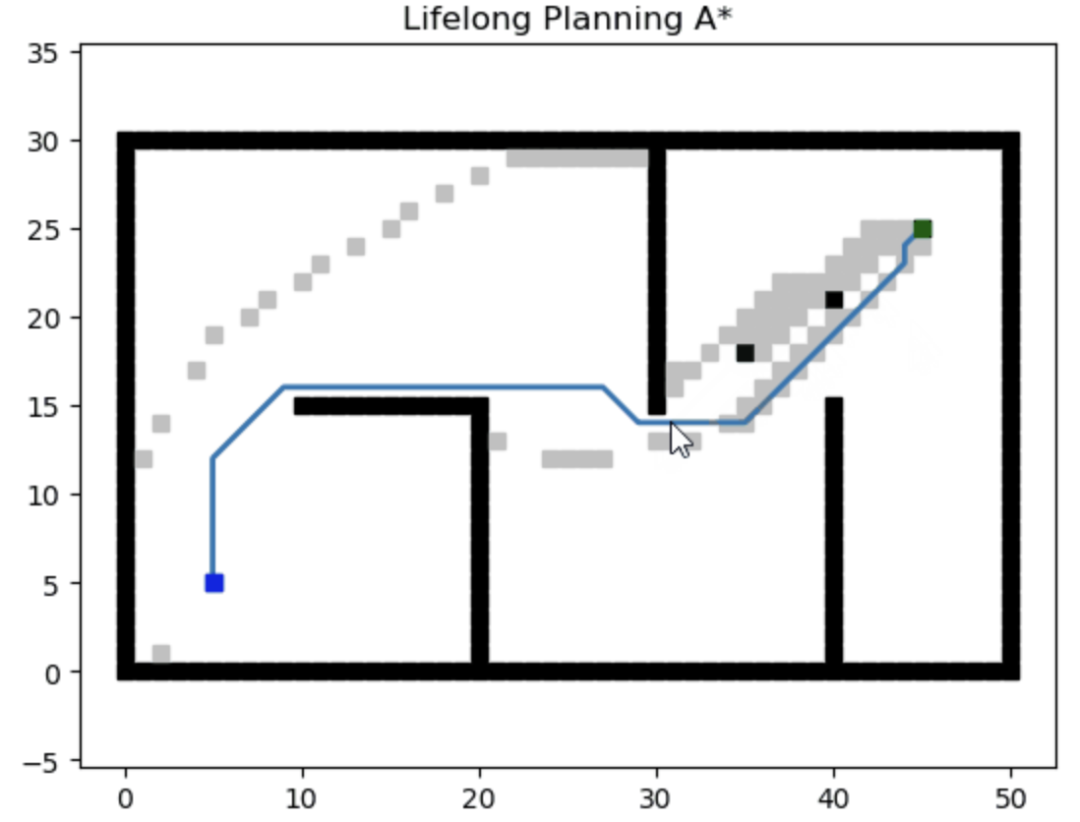
Lifelong Planning A* (LPA*)

參考文獻: Lifelong Planning A*（https://www.cs.cmu.edu/~maxim/files/aij04.pdf）

論文講解: 終身規劃A* 算法（LPA*）：Lifelong Planning A*（https://blog.csdn.net/lqzdreamer/article/details/85175372）

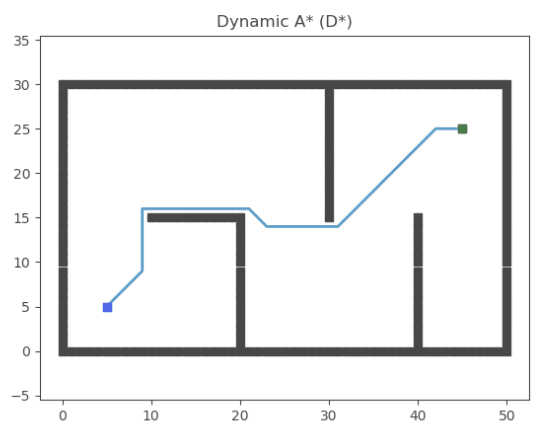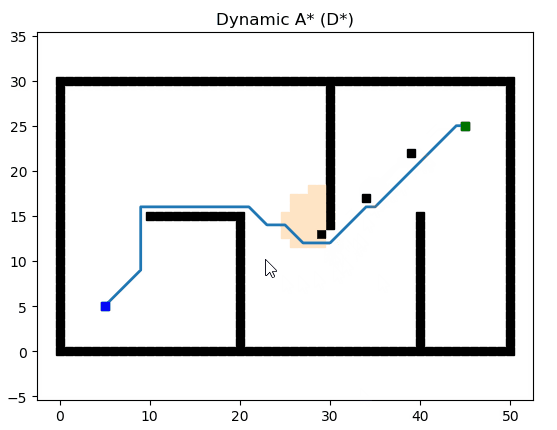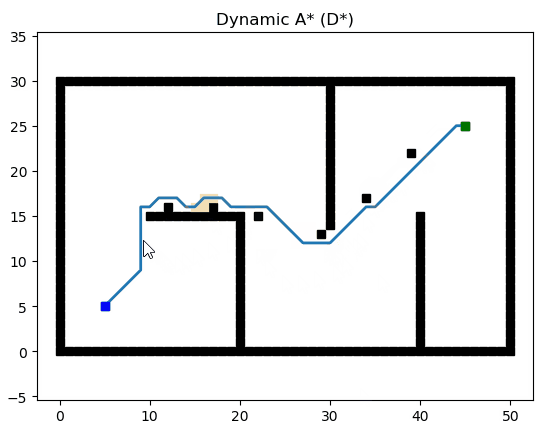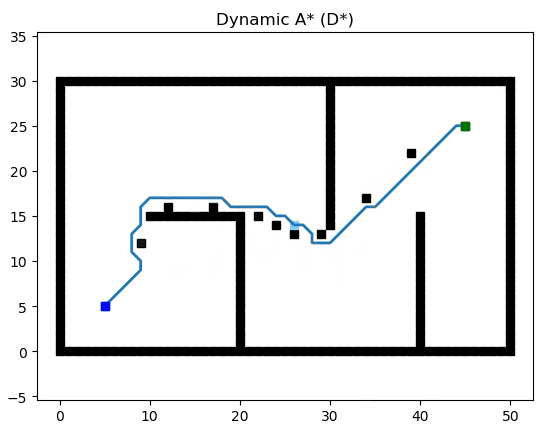
Dynamic A* (D*)

參考文獻：Optimal and Efficient Path Planning for Partially-Known Environments（http://web.mit.edu/16.412j/www/html/papers/original_dstar_icra94.pdf）

論文講解：D*路徑搜索算法原理解析及Python實現（https://blog.csdn.net/lqzdreamer/article/details/85055569）

D* Lite

D* Lite 基于 Lifelong Planning A*.

參考文獻：D* Lite（http://idm-lab.org/bib/abstracts/papers/aaai02b.pdf）

論文講解：D* Lite路徑規劃算法（https://blog.csdn.net/lqzdreamer/article/details/85108310?spm=1001.2101.3001.6650.17&utm_medium=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~Rate-17.pc_relevant_default&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~Rate-17.pc_relevant_default&utm_relevant_index=21）

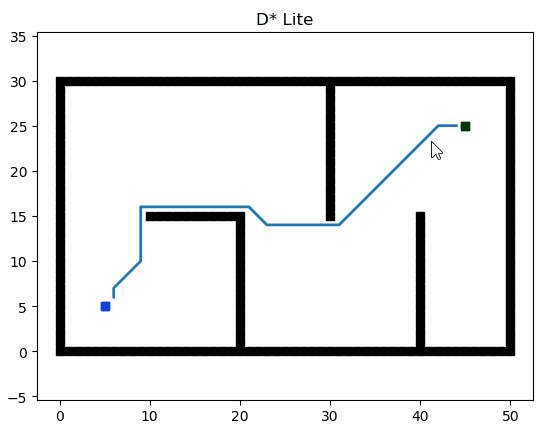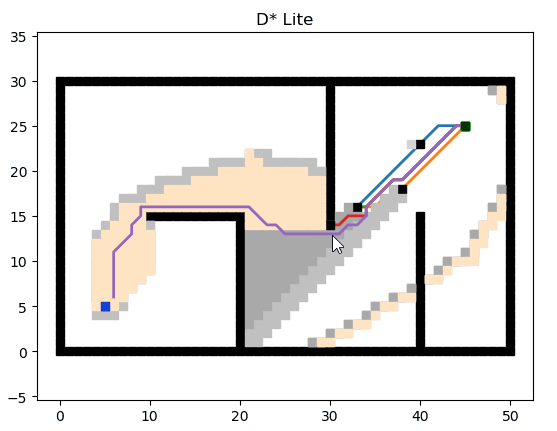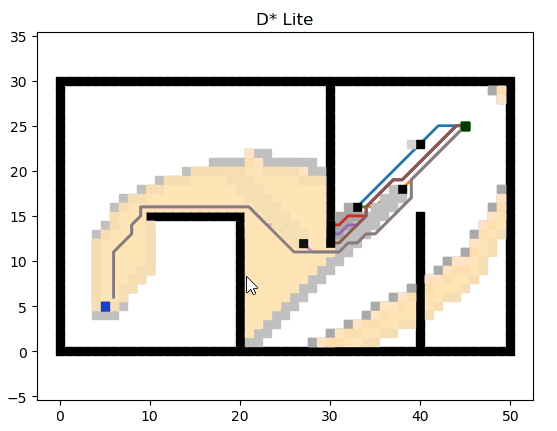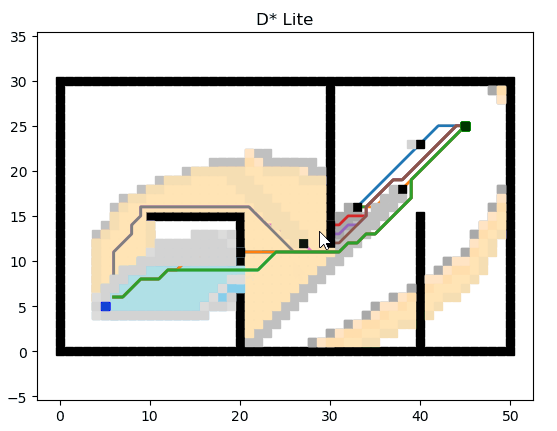
結語

限于筆者精力和能力，后半部分沒有講述的算法導向了一些熱門講解文章，大家可以參考。如果英語能力足夠，還是建議大家直接看原網站和論文，翻譯和表達總會有一些不盡如人意的地方。

編輯：黃飛

?