現在,眾多大型模型已開始支持長文本的推理,如最新的 GPT4 Turbo 能處理超過 128k 的內容,而 Baichuan2 也可應對最長為 192K 的文本。但受顯存資源約束,這些模型在訓練時并不一定會處理如此長的文本,其預訓練階段通常僅涉及約 4k 的內容。 ? 因此,如何在推理階段確保模型能處理遠超預訓練時的文本長度,已成為當前大型模型面臨的核心問題之一,我們將此問題視為大模型的外推性挑戰。 ? 而為了應對這個挑戰,最關鍵的地方就是如何優化大模型的位置編碼。在之前的文章十分鐘讀懂旋轉編碼(RoPE)中,我們已經介紹了目前應用最廣的旋轉位置編碼 RoPE。 ?
然而,那篇文章并未涉及 RoPE 在外推性方面的表現以及如何優化其外推性。恰好最近,我們組的同事在論文分享中進一步探討了大模型位置編碼的相關內容,其中包含一些我之前未曾接觸的新觀點。因此,本文旨在更全面地介紹位置編碼及其與外推性的關系。 ? 我們主要圍繞以下兩個問題展開: ? 1. RoPE 是如何實現相對位置編碼的?(如何想到的?) ? 2.?如何通過調整旋轉角(旋轉角 ),提升外推效果。
? 本文主要有以下幾個結論: ? 1. 雖然 RoPE 理論上可以編碼任意長度的絕對位置信息,但是實驗發現 RoPE 仍然存在外推問題,即測試長度超過訓練長度之后,模型的效果會有顯著的崩壞,具體表現為困惑度(Perplexity,PPL)等指標顯著上升。 ? 2. RoPE 做了線性內插(縮放位置索引,將位置 m 修改為 m/k)修改后,通常都需要微調訓練。 ? 3. 雖然外推方案也可以微調,但是內插方案微調所需要的步數要少得多。 ? 4. NTK-Aware Scaled RoPE 非線性內插,是對 base 進行修改(base 變成 )。 ?
5. NTK-Aware Scaled RoPE 在不微調的情況下,就能取得不錯的外推效果。(訓練 2048 長度的文本,就能在較低 PPL 情況下,外推 8k 左右的長文本) ? 6. RoPE 的構造可以視為一種 進制編碼,在這個視角之下,NTK-aware Scaled RoPE 可以理解為對進制編碼的不同擴增方式(擴大 k 倍表示范圍 L->k*L,那么原本 RoPE 的 β 進制至少要擴大成 進制)。
絕對位置編碼
我們先來回顧一下絕對位置編碼的問題。絕對位置編碼通過可學習的 Positional Embedding 來編碼位置信息,這種方案直接對不同的位置隨機初始化一個 postion embedding,然后與 word embedding 相加后輸入模型。postion embedding 作為模型參數的一部分,在訓練過程中進行更新。比如下面是絕對位置編碼的實現:
#?初始化
self.position_embeddings?=?nn.Embedding(config.max_position_embeddings,?config.hidden_size)
#?計算
position_embeddings?=?self.position_embeddings(position_ids)
embeddings?+=?position_embeddings
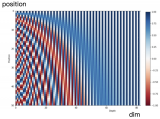
對絕對位置編碼進行可視化,如下圖所示:

▲ 圖1-1 絕對位置編碼可視化 ? 可以看到每個位置都會被區分開,并且相鄰的位置比較接近。這個方案的問題也非常明顯,不具備外推的性質。長度在預設定好之后就被固定了。 ? ? ?
正弦編碼(Sinusoidal)
基于 Sinusoidal 的位置編碼最初是由谷歌在論文 Attention is All You Need 中提出的方案,用于 Transformer 的位置編碼。具體計算方式如下所示: 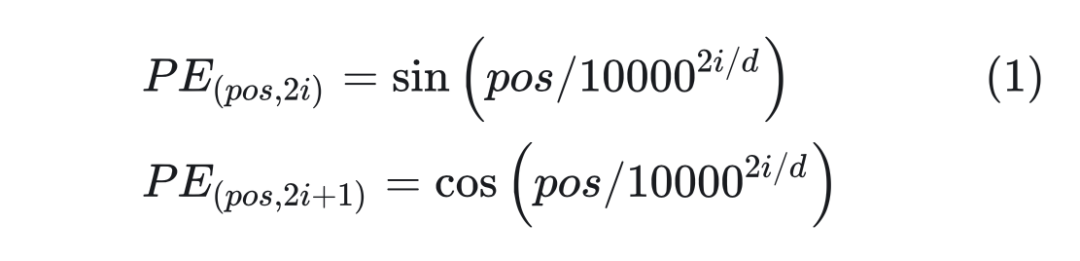 其中 pos 是位置,i 表示維度。 ? 看起來是通過 sin 和cos函數將位置編碼的取值固定在了 [-1, 1] 之前,但是為什么不用線性函數?而且這里面的10000是怎么想到的? ? 谷歌在論文里面給出了解釋: ?
其中 pos 是位置,i 表示維度。 ? 看起來是通過 sin 和cos函數將位置編碼的取值固定在了 [-1, 1] 之前,但是為什么不用線性函數?而且這里面的10000是怎么想到的? ? 谷歌在論文里面給出了解釋: ?
具有相對位置表達能力:Sinusoidal 可以學習到相對位置,對于固定位置距離的 k,PE(i+k) 可以表示成 PE(i) 的線性函數。
兩個位置向量的內積只和相對位置 k 有關。
Sinusoidal 編碼具有對稱性。
隨著 k 的增加,內積的結果會直接減少,即會存在遠程衰減。
下面我們來分析一下為什么會有上面四點結論。
2.1 相對位置表達能力
Sinusoidal 可以學習到相對位置,對于固定位置距離的 k,PE(i+k) 可以表示成 PE(i) 的線性函數。證明如下:
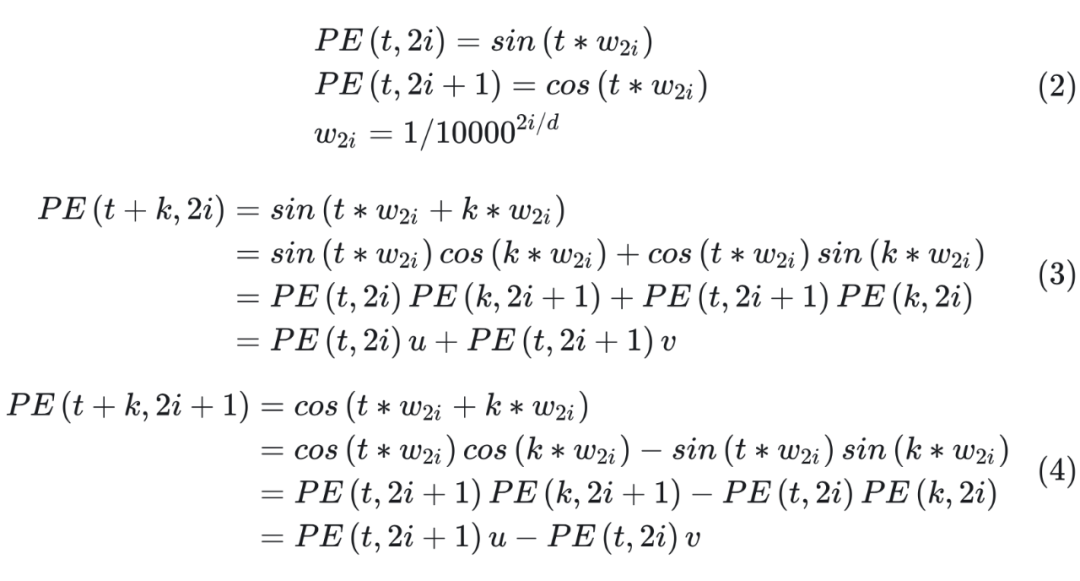
其中 u, v 為關于 k 的常數,所以可以證明 PE(i+k) 可以由 PE(i) 線性表示。?
2.2 內積只和相對位置k有關
Attention 中的重要操作就是內積。計算兩個位置的內積 PE(t+k)PE(t) 如下所示:
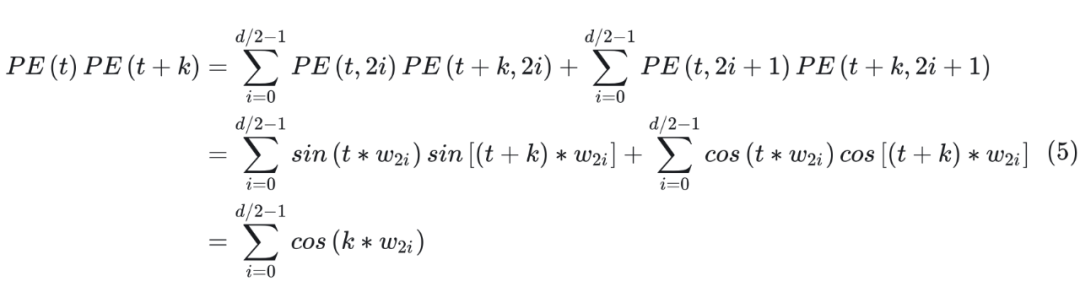
可以看到,最終的結果是關于 k 的一個常數。這表明兩個位置向量的內積只和相對位置 k 有關。 ? 通過計算,很容易得到 PE(t+k)PE(t) = PE(t)PE(t-k),這表明 Sinusoidal 編碼具有對稱性。
2.3 遠程衰減
可以發現,隨著 k 的增加,位置向量的內積結果會逐漸降低,即會存在遠程衰減。如下圖所示:
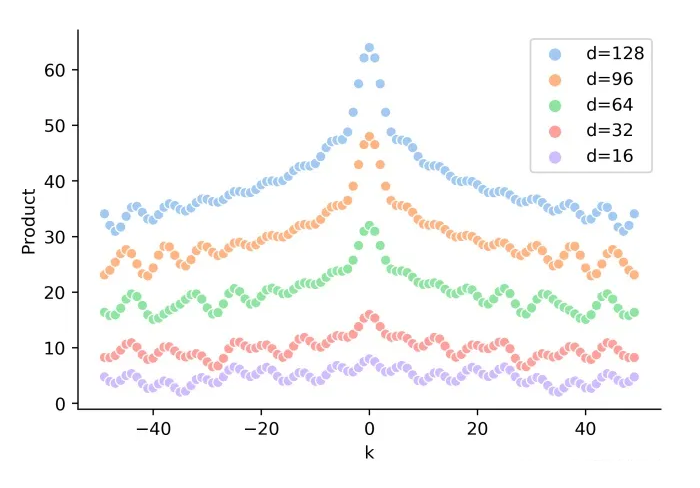
▲ 圖2-1 隨著相對距離 k 的增加,位置向量內積 PE(t)PE(t+k) 逐漸降低
2.4 為什么選擇參數base=10000
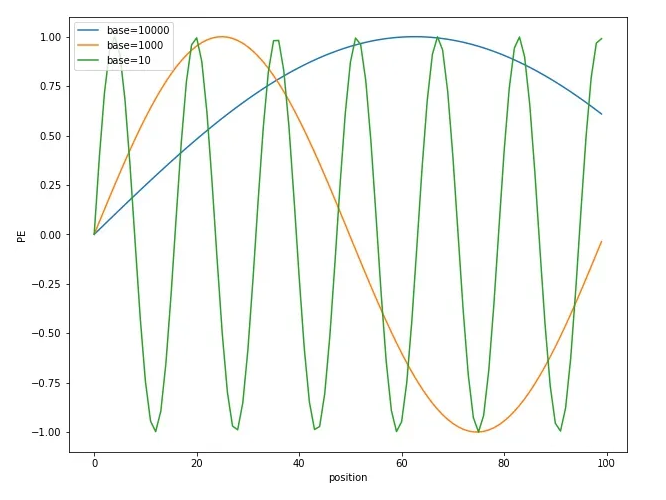
選擇 sin,cos 是因為可以表達相對位置,以及具備遠程衰減。但是 sin/cos 里面的參數 10000 是如何來的? ? 這里可以從 sin/cos 的周期性角度進行分析。分析周期可以發現,維度i的周期為 ,其中 0<=i
▲ 圖2-2 不同 base 下的 position embedding 取值 ? 可以看到隨著 base 的變大,周期會明顯變長。Transformer 選擇比較大的 base=10000,可能是為了能更好的區分開每個位置。 ? 備注:解釋下為什么周期大能更好區分位置 ? 從圖 2-2 可以看出,base 越大,周期越大。而周期越大,在 position 從 0~100 范圍內,只覆蓋了不到半個周期,這使得重復值少;而周期小的,覆蓋了多個周期,就導致不同位置有大量重復的值。
2.5 正弦編碼是否真的具備外推性?
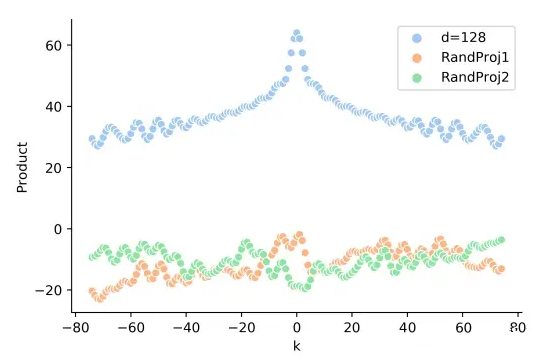
在前面的圖 2-1 中,似乎 Sinusoidal 只和相對位置有關。但是實際的 Attention 計算中還需要與 attention 的權重 W 相乘,即 ,這時候內積的結果就不能反映相對距離,如下圖所示:
▲ 圖2-3 真實的 q,k 向量內積和相對距離之間,沒有遠程衰減性
旋轉位置編碼(RoPE)
3.1 什么是好的位置編碼
既然前面的絕對位置編碼和 Sinusoidal 編碼都不是好的位置編碼,那么什么才是好的位置編碼? ? 理想情況下,一個好的位置編碼應該滿足以下條件: ?
每個位置輸出一個唯一的編碼
具備良好的外推性
任何位置之間的相對距離在不同長度的句子中應該是一致的
這兩條比較好理解,最后一條是指如果兩個 token 在句子 1 中的相對距離為 k,在句子 2 中的相對距離也是 k,那么這兩個句子中,兩個 token 之間的相關性應該是一致的,也就是 attention_sample1 (token1, token2) = attention_sample2 (token1, token2)。
▲ 圖3-1 平移性 ? 而 RoPE 正是為了解決上面三個問題而提出的。
3.2 RoPE如何解決內積只和相對位置有關
RoPE 旋轉位置編碼是蘇神在論文 RoFormer 中提出的,也是目前大模型廣泛采用的一種位置編碼方式。這種編碼不是作用在 embedding 的輸入層,而是作用在與 Attention 的計算中。 ? 假設位置 m 的位置編碼為 ,位置 n 的位置編碼為 ,如果使用之前的絕對位置編碼方式,那么兩個位置之間的 attention 可以表示為:
其中 表示位置 m 的旋轉矩陣。 ? 將 d=2 擴展到多維,旋轉矩陣表示如下:
▲ 圖3-2 為什么 RoPE?選擇 方式進行位置編碼
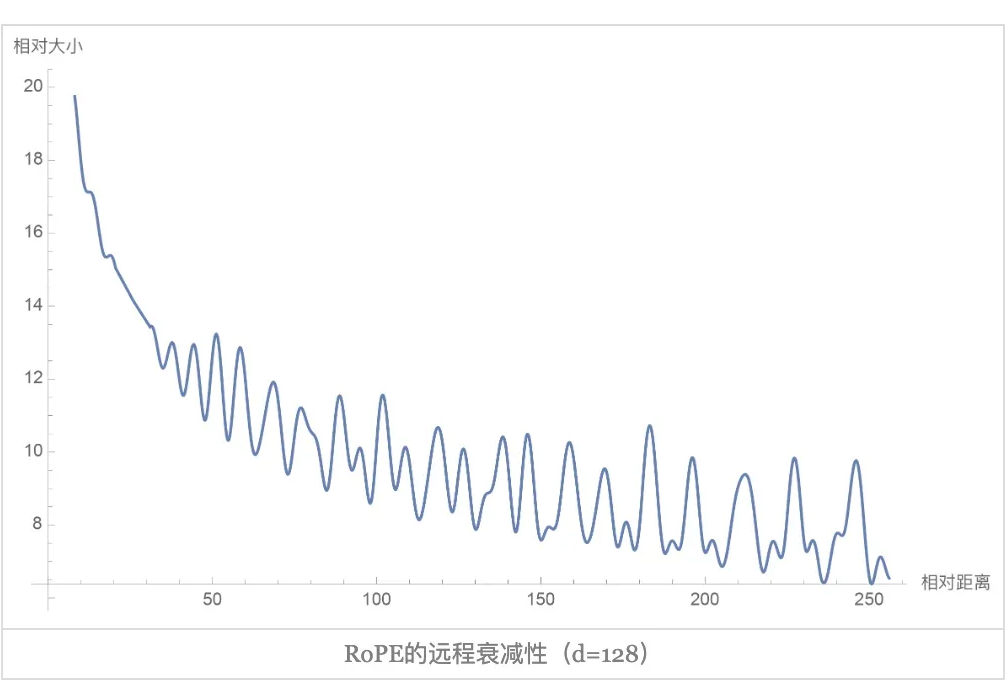
3.3 RoPE的遠程衰減
▲ 圖3-3 RoPE 的遠程衰減 ? 從圖中我們可以看到隨著相對距離的變大,內積結果有衰減趨勢的出現。因此,選擇 ,確實能帶來一定的遠程衰減性。論文中還試過以 為初始化,將 視為可訓練參數,然后訓練一段時間后發現 并沒有顯著更新,因此干脆就直接固定 了。 ? ? ?
調整旋轉角提升外推效果
雖然 RoPE 理論上可以編碼任意長度的絕對位置信息,并且 sin/cos 計算就能將任意長度的相對位置信息表達出來,但是實驗發現 RoPE 仍然存在外推問題,即測試長度超過訓練長度之后,模型的效果會有顯著的崩壞,具體表現為困惑度(Perplexity,PPL)等指標顯著上升。 ? 對此,就有很多人提出了如何擴展 LLM 的 Context 長度,比如有人實驗了“位置線性內插”的方案,顯示通過非常少的長文本微調,就可以讓已有的 LLM 處理長文本。 ? 幾乎同時,Meta 也提出了同樣的思路,在論文 Extending Context Window of Large Language Models via Positional Interpolation 中提出了位置線性內插(Position Interpolation,PI)。 ? 隨后,又有人提出了 NTK-aware Scaled RoPE,實現了不用微調就可以擴展 Context 長度的效果。 ? 從 Sinusoidal 編碼到旋轉位置編碼 RoPE, 的取值一直都是 ,也就是base = 10000。而最新的位置線性內插和 NTK 都打破了這一傳統。
4.1 位置線性內插(Position Interpolation,PI)
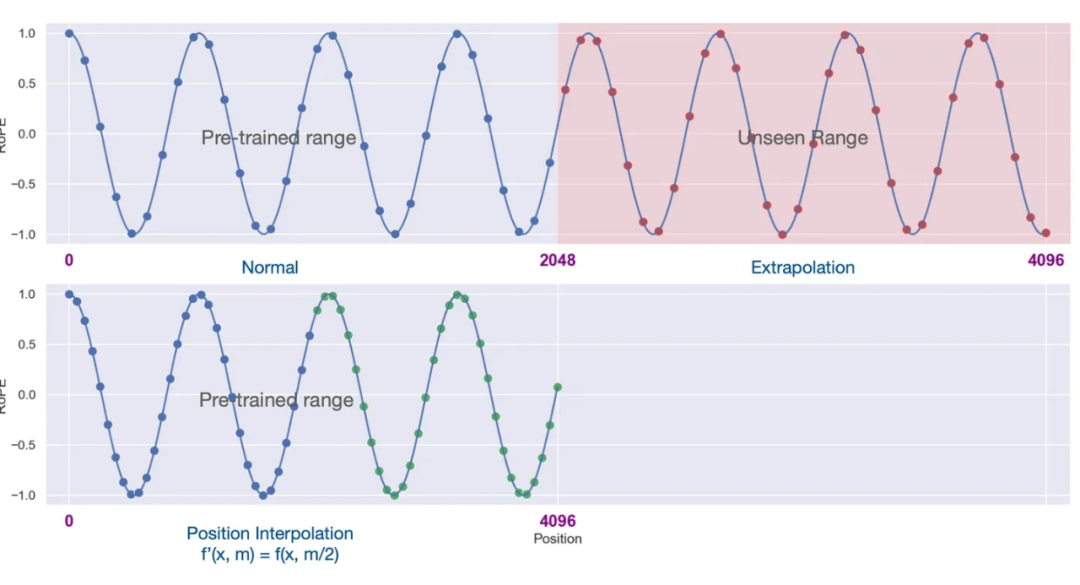
傳統的 RoPE 算法在超出最大距離后,PPL 就會爆炸,因此直接推廣的效果一定是很差的,因此 Position Interpolation 繞過了推廣的限制,通過內插的方法,如下圖所示。
▲ 圖4-1 RoPE 位置線性內插(base 和位置線性內插的效果對比)
圖 4-1 是關于“位置線性內插(Position Interpolation)”方法的圖示說明。對于預訓練 2048 長度,外推 4096 長度: ? 左上角圖示:
這部分是 LLM 預訓練的長度。
藍色點代表輸入的位置索引,它們都在 0 到 2048 的范圍內,即預訓練范圍內。
這意味著給模型提供的輸入序列長度沒有超過它預訓練時的最大長度。
右上角圖示:
這部分展示了所謂的“長度外推”(Extrapolation)情況。
在這種情況下,模型被要求處理位置索引超出 2048 的情況,直到 4096(由紅色點表示)。
這些位置對于模型來說是“未見過的”,因為在預訓練時它們并沒有涉及。
當模型遇到這種更長的輸入序列時,其性能可能會受到影響,因為它沒有被優化來處理這種情況。
左下角圖示:
這部分展示了“位置線性內插”方法的應用。
為了解決模型處理更長序列時的問題,研究者們提出了一個策略:將位置索引本身進行下采樣或縮放。
具體來說,他們將原本在 [0, 4096] 范圍內索引(由藍色和綠色點表示)縮放到 [0, 2048] 的范圍內。
通過這種方式,所有的位置索引都被映射回了模型預訓練時的范圍內,從而幫助模型更好地處理這些原本超出其處理能力的輸入序列。
我們再舉一個例子,base=10000,d=2048,對于 token embedding 第 2000 維,RoPE 為:
base?=?10000
由于 ,因此相當于是擴大了 base,縮小了 。 從小到大對應低頻到高頻的不同特征(周期 ,頻率 )。 ? 下面是實驗結果:
▲ 圖4-3 微調少量長文本,位置線性內插就能推理長文本 ? 從圖 4-2 可以看出,使用 10000 條樣本,直接進行微調長度為 8192 的文本,外推長度只能到 2560;而只用 1000 條樣本,在微調中使用位置線性內插,外推長度就可以達到 8192。
4.2 NTK-Aware Scaled RoPE
位置線性內插雖然效果不錯,但是插值方法是線性的,這種方法在處理相近的 token 時可能無法準確區分它們的順序和位置。因此,研究者提出了一種非線性的插值方案,它改變 RoPE 的 base 而不是比例,從而改變每個 RoPE 維度向量與下一個向量的“旋轉”速度。 ? 由于它不直接縮放傅里葉特征,因此即使在極端情況下(例如拉伸 100 萬倍,相當于 20 億的上下文大小),所有位置都可以完美區分。 ? 新的方法被稱為 “NTK-Aware Scaled RoPE”,它允許 LLaMA 模型在無需任何微調且困惑度降低到最小的情況下擴展上下文長度。這種方法基于 Neural Tangent Kernel(NTK)理論和 RoPE 插值進行改進。 ? NTK-Aware Scaled RoPE 在 LLaMA 7B(Context 大小為 2048)模型上進行了實驗驗證,結果表明在不需要對 4096 Context 進行微調的情況下,困惑度可以降低到非常小。 ? NTK-Aware Scaled RoPE 的計算非常簡單,如下所示:
可以看到,公式(15)只是對 base 進行了放大,但是實驗效果卻非常好。為什么會取得這樣的效果? ? 為了解開這個謎底,我們需要理解 RoPE 的構造可以視為一種 進制編碼,在這個視角之下,NTK-aware Scaled RoPE 可以理解為對進制編碼的不同擴增方式。
4.2.1 進制表示 假設我們有一個 1000 以內(不包含 1000)的整數 n 要作為條件輸入到模型中,那么要以哪種方式比較好呢? ? 最樸素的想法是直接作為一維浮點向量輸入,然而 0~999 這涉及到近千的跨度,對基于梯度的優化器來說并不容易優化得動。那縮放到 0~1 之間呢?也不大好,因為此時相鄰的差距從 1 變成了 0.001,模型和優化器都不容易分辨相鄰的數字。總的來說,基于梯度的優化器只能處理好不大不小的輸入,太大太小都容易出問題。 ? 所以,為了避免這個問題,我們還需要繼續構思新的輸入方式。在不知道如何讓機器來處理時,我們不妨想想人是怎么處理呢。對于一個整數,比如 759,這是一個 10 進制的三位數,每位數字是 0~9。 ? 既然我們自己都是用 10 進制來表示數字的,為什么不直接將 10 進制表示直接輸入模型呢?也就是說,我們將整數n以一個三維向量 [a,b,c] 來輸入,a,b,c 分別是n的百位、十位、個位。這樣,我們既縮小了數字的跨度,又沒有縮小相鄰數字的差距,代價是增加了輸入的維度——剛好,神經網絡擅長處理高維數據。 ? 如果想要進一步縮小數字的跨度,我們還可以進一步縮小進制的基數,如使用 8 進制、6 進制甚至 2 進制,代價是進一步增加輸入的維度。
4.2.2 直接外推 假設我們還是用三維 10 進制表示訓練了模型,模型效果還不錯。然后突然來了個新需求,將 n 上限增加到 2000 以內,那么該如何處理呢? ? 如果還是用 10 進制表示的向量輸入到模型,那么此時的輸入就是一個四維向量了。然而,原本的模型是針對三維向量設計和訓練的,所以新增一個維度后,模型就無法處理了。有一種方法是提前預留好足夠多的維度,訓練階段設為 0,推理階段直接改為其他數字,這就是外推(Extrapolation)。
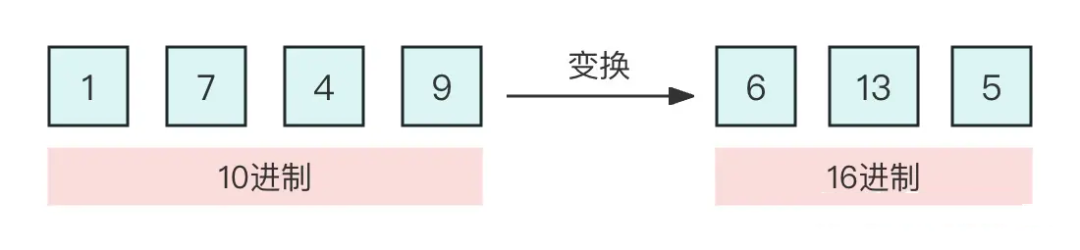
▲ 位置線性內插 ? 當然,外推方案也可以微調,但是內插方案微調所需要的步數要少得多,因為很多場景(比如位置編碼)下,相對大小(或許說序信息)更加重要,換句話說模型只需要知道 874.5 比 874 大就行了,不需要知道它實際代表什么多大的數字。而原本模型已經學會了 875 比 874 大,加之模型本身有一定的泛化能力,所以再多學一個 874.5 比 874 大不會太難。 ? 不過,內插方案也不盡完美,當處理范圍進一步增大時,相鄰差異則更小,并且這個相鄰差異變小集中在個位數,剩下的百位、十位,還是保留了相鄰差異為 1。換句話說,內插方法使得不同維度的分布情況不一樣,每個維度變得不對等起來,模型進一步學習難度也更大。 4.2.4 進制轉換 有沒有不用新增維度,又能保持相鄰差距的方案呢? ? 有,就是進制轉換。三個數字的 10 進制編碼可以表示 0~999,如果是 16 進制呢?它最大可以表示 。所以,只需要轉到 16 進制,如 1749 變為 [6,13,5],那么三維向量就可以覆蓋目標范圍,代價是每個維度的數字從 0~9 變為 0~15。
▲ 圖4-5 進制轉換 ? ? 剛才說到,我們關心的場景主要利用序信息,原來訓練好的模型已經學會了 875 > 874,而在 16 進制下同樣有 875 > 874,比較規則是一模一樣的(模型根本不知道你輸入的是多少進制)。 ? 唯一擔心的是每個維度超過 9 之后(10~15)模型還能不能正常比較,但事實上一般模型也有一定的泛化能力,所以每個維度稍微往外推一些是沒問題的。所以,這個轉換進制的思路,甚至可能不微調原來模型也有效!另外,為了進一步縮窄外推范圍,我們還可以換用更小的 進制而不是 16 進制。 ? 接下來我們將會看到,這個進制轉換的思想,實際上就對應著前面的 NTK-aware scaled RoPE。 4.2.5 位置編碼 為了建立起它們的聯系,我們先要建立如下結果: ? ?
位置 n 的旋轉位置編碼(RoPE),本質上就是數字 n 的 β 進制編碼
看上去可能讓人意外,因為兩者表面上迥然不同。但事實上,兩者的運算有著相同的關鍵性質。為了理解這一點,我們首先回憶一個 10 進制的數字 n,我們想要求它的 β 進制表示的(從右往左數)第 m 位數字,方法是:
對比公式(16)和(17),兩者都有相同的 ,并且 mod,cos,sin 都是周期函數。所以,除掉取整函數這個無關緊要的差異外,RoPE/Sinusoidal 位置編碼類比為位置 n 的 進制編碼。 ? 建立起這個聯系后,直接外推方案就是啥也不改,位置線性內插就是將 n 換成 n/k,其中 k 是要擴大的倍數,這就是 Meta 的論文所實驗的 Positional Interpolation,里邊的實驗結果也證明了外推比內插確實需要更多的微調步數。 ? 至于進制轉換,就是要擴大 k 倍表示范圍,那么原本的 β 進制至少要擴大成 進制(公式(17)雖然是 d 維向量,但 cos,sin 是成對出現的,所以相當于 d/2 位 進制表示,因此要開 d/2 次方而不是 d 次方),或者等價地原來的底數 10000 換成 10000k,這基本上就是 NTK-aware Scaled RoPE。 ? 跟前面討論的一樣,由于位置編碼更依賴于序信息,而進制轉換基本不改變序的比較規則,所以 NTK-aware Scaled RoPE 在不微調的情況下,也能在更長 Context 上取得不錯的效果。 4.2.6 NTK-Aware Scaled RoPE和RoPE β進制的關系 所以,這跟 NTK 有什么關系呢?NTK 全稱是 “Neural Tangent Kernel”,具體原理可以參考《從動力學角度看優化算法:SGD ≈ SVM?》。 ? 要說上述結果跟 NTK 的關系,更多的是提出者的學術背景緣故,提出者對《Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains》等結果比較熟悉,里邊利用 NTK 相關結果證明了神經網絡無法直接學習高頻信號,解決辦法是要將它轉化為 Fourier 特征——其形式就跟公式(17)的 Sinusoidal 位置編碼差不多。 ? 所以,提出者基于 NTK 相關結果的直覺,推導了 NTK-aware Scaled RoPE。假設要擴大 k 倍范圍表示,根據 NTK-Aware Scaled RoPE,高頻外推、低頻內插。具體來說,公式(17)最低頻是 ,引入參數 變為 ,讓他與內插一致,即:
▲ 圖4-6 不同插值方法的效果(這里的 scale 是指位置插值中擴大的倍數 k,alpha 是指 NTK 中的 lambda 參數或者是公式(15)中的 alpha 參數)
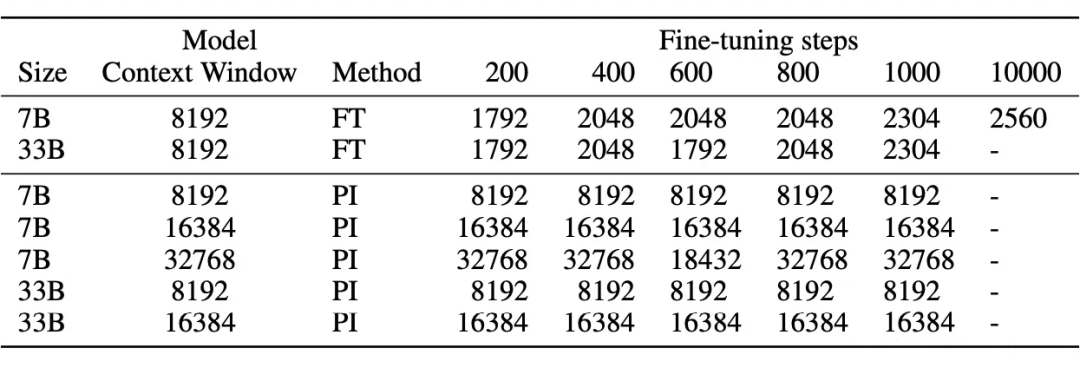
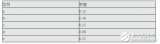
從圖中可以看出在 時,NTK 可以在比較小的 PPL 情況下,外推 8k 左右的長文本。 ? 再看一下蘇神的實驗結論(表中的數據表示準確率),當 k=8 時,結論如下:
上面的結論是沒有經過長文本微調的結果,其中 Baseline 就是外推,PI(Positional Interpolation)就是 Baseline 基礎上改內插,NTK-RoPE 就是 Baseline 基礎上改 NTK-aware Scaled RoPE。 ? 從表中我們得出以下結論: ?
1、直接外推的效果不大行
2、內插如果不微調,效果也很差
3、NTK-RoPE 不微調就取得了不錯的外推結果 ? ? ?
總結
目前大模型處理長文本的能力成為研究的熱點,由于收集長文本的語料非常的困難,因此如何不用微調或者少量微調,就能外推 k 倍的長文本,成為大家的關注的焦點。 ? 本文詳細介紹了 Meta 的位置線性內插和 NTK 兩種優化外推的方法,結合蘇神對 RoPE 解釋為一種 進制編碼,那么位置線性內插和 NTK 都可以理解為對進制編碼的不同擴增方式。 ?
審核編輯:黃飛
?

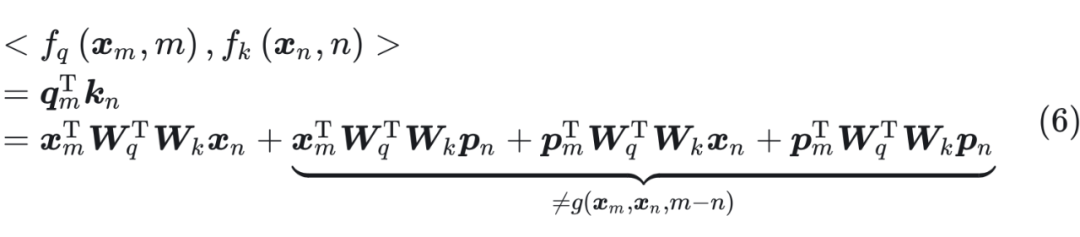 后面的三項都是和絕對位置位置 m,n 有關,無法表示成 m-n 的形式。 ? 因此,我們需要找到一種位置編碼,使得公式(6)表示為如下的形式:
后面的三項都是和絕對位置位置 m,n 有關,無法表示成 m-n 的形式。 ? 因此,我們需要找到一種位置編碼,使得公式(6)表示為如下的形式: 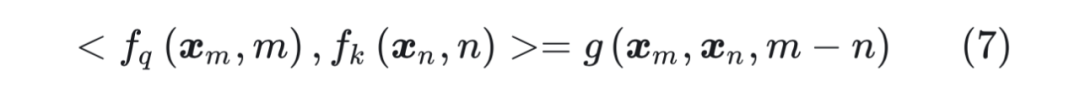 接下來的目標就是找到一個等價的位置編碼方式,從而使得上述關系成立。 ? 假定現在詞嵌入向量的維度是兩維 d=2,這樣就可以利用上 2 維度平面上的向量的幾何性質,然后論文中提出了一個滿足上述關系的 f 和 g 的形式如下:
接下來的目標就是找到一個等價的位置編碼方式,從而使得上述關系成立。 ? 假定現在詞嵌入向量的維度是兩維 d=2,這樣就可以利用上 2 維度平面上的向量的幾何性質,然后論文中提出了一個滿足上述關系的 f 和 g 的形式如下: 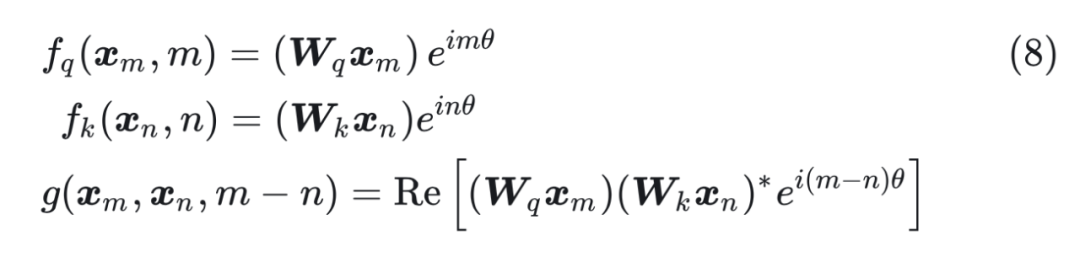 這里面 Re 表示復數的實部。 ? 進一步地, 可以表示成下面的式子:
這里面 Re 表示復數的實部。 ? 進一步地, 可以表示成下面的式子:
 總結來說,RoPE 的 self-attention 操作的流程是:對于 token 序列中的每個詞嵌入向量,首先計算其對應的 query 和 key 向量,然后對每個 token 位置都計算對應的旋轉位置編碼,接著對每個 token 位置的 query 和 key 向量的元素按照兩兩一組應用旋轉變換,最后再計算 query 和 key 之間的內積得到 self-attention 的計算結果。 ? RoPE 為什么會想到用 進行位置編碼?來看一下蘇神現身說法(相乘后可以表達成差的形式,所以可能可以實現相對位置編碼):
總結來說,RoPE 的 self-attention 操作的流程是:對于 token 序列中的每個詞嵌入向量,首先計算其對應的 query 和 key 向量,然后對每個 token 位置都計算對應的旋轉位置編碼,接著對每個 token 位置的 query 和 key 向量的元素按照兩兩一組應用旋轉變換,最后再計算 query 和 key 之間的內積得到 self-attention 的計算結果。 ? RoPE 為什么會想到用 進行位置編碼?來看一下蘇神現身說法(相乘后可以表達成差的形式,所以可能可以實現相對位置編碼):
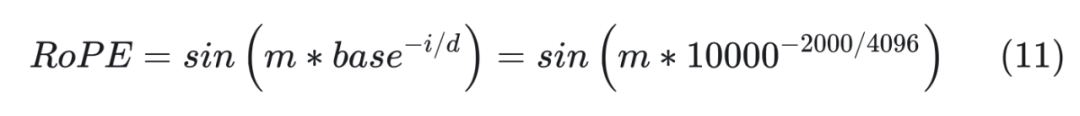
i?=?2000
d?=?4096
pos?=?list(range(1,?2049))
w?=?math.pow(base,?-i/d)
v?=?np.array([math.cos(p?*?w)?for?p?in?pos])
index?=?sorted(random.sample(pos,?15))
#?繪制曲線??
plt.figure(figsize=(10,?4))??#?創建一個新的圖形??
plt.scatter([pos[-1]],?[v[-1]])
index_to_highlight?=?-1????
#?添加注釋顯示坐標值??
plt.annotate(f'({pos[index_to_highlight]},?{v[index_to_highlight]:.2f})',??
?????????????xy=(pos[index_to_highlight],?v[index_to_highlight]),???
?????????????xytext=(10,?-10),??#?文本位置相對于注釋點的偏移量??
?????????????textcoords="offset?points",??#?文本坐標的參照系(基于點的偏移)??
#??????????????arrowprops=dict(arrowstyle="-|>",?connectionstyle="arc3,rad=0.2")
????????????)??#?箭頭樣式和連接樣式??
plt.plot(pos,?v,?'-')??#?繪制第一條曲線?
plt.scatter(index,?v[index],?color='blue',?s=20,?label='pre-trained?RoPE')??#?繪制第一條曲線?
pos?=?list(range(2048,?4097))
w?=?math.pow(base,?-i/d)
v?=?np.array([math.cos(p?*?w)?for?p?in?pos])
index?=?sorted(random.sample(pos,?15))
v_?=?np.array([math.cos(p?*?w)?for?p?in?index])
plt.plot(pos,?v,?'green')??#?繪制第一條曲線?
plt.scatter(index,?v_,?color='r',?s=20,?label='Extrapolation?RoPE')??#?繪制第一條曲線?
plt.annotate(f'({pos[index_to_highlight]},?{v[index_to_highlight]:.2f})',????
?????????????xy=(pos[index_to_highlight],?v[index_to_highlight]),???
?????????????xytext=(10,?-10),??#?文本位置相對于注釋點的偏移量??
?????????????textcoords="offset?points",??#?文本坐標的參照系(基于點的偏移)??
#??????????????arrowprops=dict(arrowstyle="-|>",?connectionstyle="arc3,rad=0.2")
????????????)??#?箭頭樣式和連接樣式?
plt.grid(axis='y')
#?添加圖例??
plt.legend()??
#?顯示圖形??
plt.show()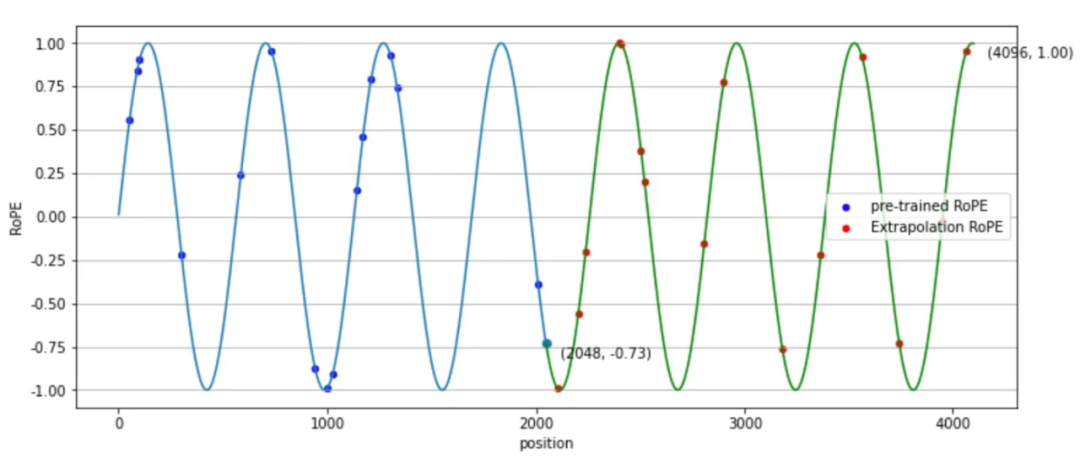 ▲ 圖4-2 RoPE位置編碼 ? 從圖 4-2 可以看出,在外推(Extrapolation)時,紅色點超出了預訓練時的位置編碼。 ? 為了解決這個問題,位置線性內插的核心思想是通過縮放位置索引,使得模型能夠處理比預訓練時更長的序列,而不損失太多性能。
▲ 圖4-2 RoPE位置編碼 ? 從圖 4-2 可以看出,在外推(Extrapolation)時,紅色點超出了預訓練時的位置編碼。 ? 為了解決這個問題,位置線性內插的核心思想是通過縮放位置索引,使得模型能夠處理比預訓練時更長的序列,而不損失太多性能。 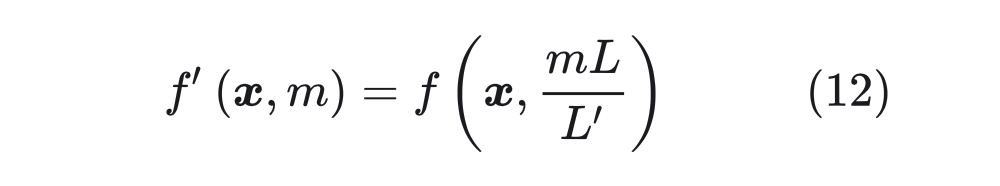 其中 x 是 token embedding,m 是位置。對于一個超過之前最大長度 L 的樣本(長度為 L’),通過縮放將所有位置映射回 L 區間,每個位置都不再是整數。通過這種方式在長樣本區間訓練 1000 步,就能很好的應用到長樣本上。 ? 我們看一下新的位置編碼后,設?,內積可以表示為:
其中 x 是 token embedding,m 是位置。對于一個超過之前最大長度 L 的樣本(長度為 L’),通過縮放將所有位置映射回 L 區間,每個位置都不再是整數。通過這種方式在長樣本區間訓練 1000 步,就能很好的應用到長樣本上。 ? 我們看一下新的位置編碼后,設?,內積可以表示為: 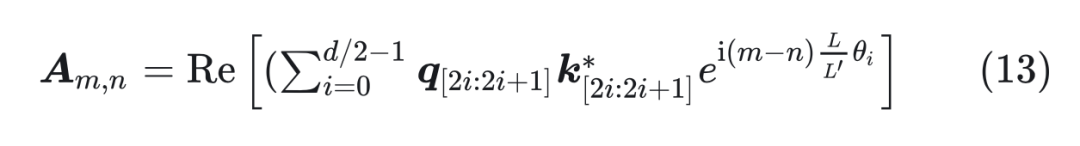 其中 可以表示為 , 中的“*”表示共軛,可以表示為 。這里面 可以改寫為:
其中 可以表示為 , 中的“*”表示共軛,可以表示為 。這里面 可以改寫為: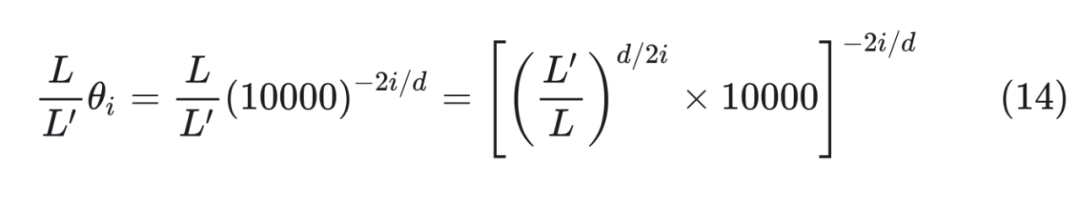
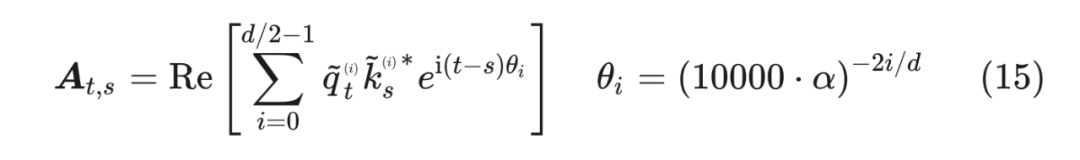
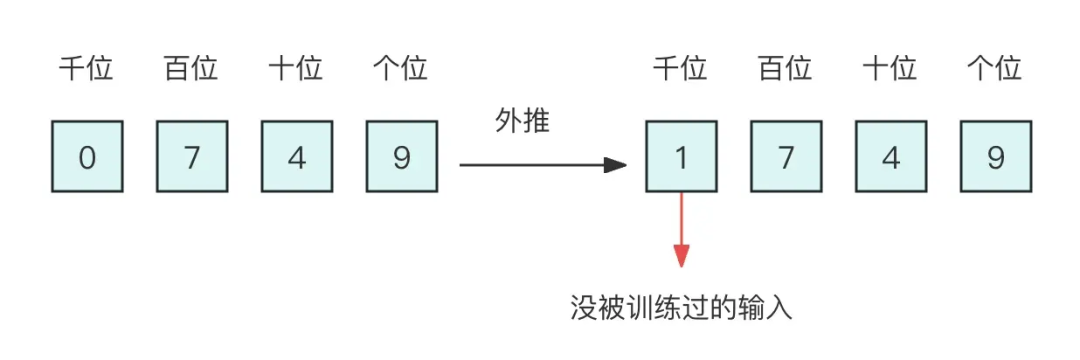 ▲ 圖4-4 直接外推 ? 然而,訓練階段預留的維度一直是 0,如果推理階段改為其他數字,效果不見得會好,因為模型對沒被訓練過的情況不一定具有適應能力。也就是說,由于某些維度的訓練數據不充分,所以直接進行外推通常會導致模型的性能嚴重下降。 4.2.3 線性內插 于是,有人想到了將外推改為內插(Interpolation),簡單來說就是將 2000 以內壓縮到 1000 以內,比如通過除以 2,1749 就變成了 874.5,然后轉為三維向量 [8,7,4.5] 輸入到原來的模型中。從絕對數值來看,新的 [7,4,9] 實際上對應的是1498,是原本對應的 2 倍,映射方式不一致;從相對數值來看,原本相鄰數字的差距為 1,現在是 0.5,最后一個維度更加“擁擠”。 ? 所以,做了內插修改后,通常都需要微調訓練,以便模型重新適應擁擠的映射關系。
▲ 圖4-4 直接外推 ? 然而,訓練階段預留的維度一直是 0,如果推理階段改為其他數字,效果不見得會好,因為模型對沒被訓練過的情況不一定具有適應能力。也就是說,由于某些維度的訓練數據不充分,所以直接進行外推通常會導致模型的性能嚴重下降。 4.2.3 線性內插 于是,有人想到了將外推改為內插(Interpolation),簡單來說就是將 2000 以內壓縮到 1000 以內,比如通過除以 2,1749 就變成了 874.5,然后轉為三維向量 [8,7,4.5] 輸入到原來的模型中。從絕對數值來看,新的 [7,4,9] 實際上對應的是1498,是原本對應的 2 倍,映射方式不一致;從相對數值來看,原本相鄰數字的差距為 1,現在是 0.5,最后一個維度更加“擁擠”。 ? 所以,做了內插修改后,通常都需要微調訓練,以便模型重新適應擁擠的映射關系。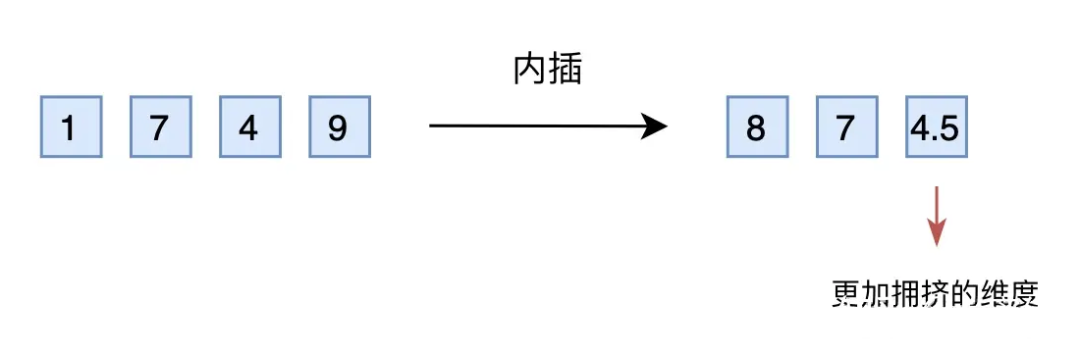
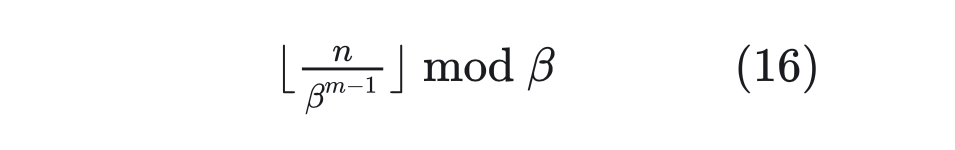 也就是先除以 次方,然后求模(余數)。然后再來回憶 RoPE,它的構造基礎是 Sinusoidal 位置編碼,可以改寫為:
也就是先除以 次方,然后求模(余數)。然后再來回憶 RoPE,它的構造基礎是 Sinusoidal 位置編碼,可以改寫為: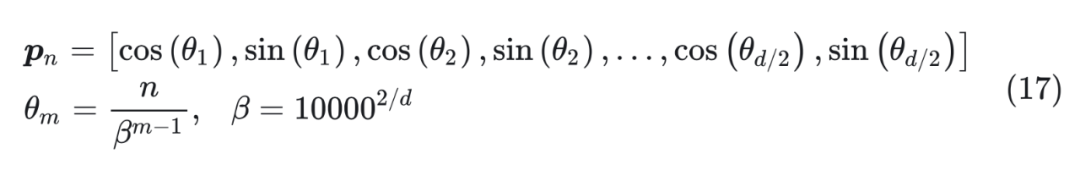
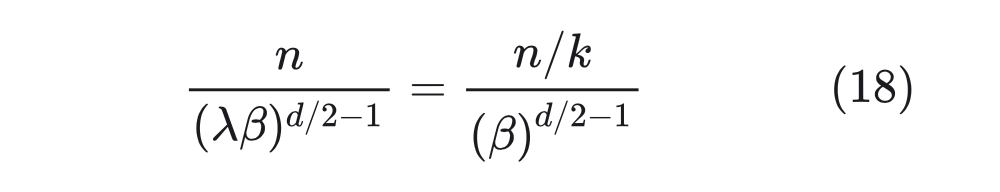 那么得到 。至于最高頻是 項,引入 變為 ,由于 d 很大,,所以它還是接近于初始值 ,等價于外推。 ? 所以這樣的方案簡單巧妙地將外推和內插結合了起來。另外,由于 d 比較大,因此 跟 差別不大,所以它跟前面基于進制思想提出的解 是基本一致的。還有,從提出者這個思想來看,任意能實現“高頻外推、低頻內插”的方案都是可以的,并非只有上述引入 的方案。 ? 如果從前面的進制轉換的角度分析,直接外推會將外推壓力集中在“高位(m 較大)”上,而位置內插則會將“低位(m 較小)”的表示變得更加稠密,不利于區分相對距離。而 NTK-aware Scaled RoPE 其實就是進制轉換,它將外推壓力平攤到每一位上,并且保持相鄰間隔不變,這些特性對明顯更傾向于依賴相對位置的 LLM 來說是非常友好和關鍵的,所以它可以不微調也能實現一定的效果。 ? 從公式(17)可以看出,cos,sin 事實上是一個整體,所以它實際只有 d/2 位,也就是說它相當于位置 n 的 d/2 位 進制。如果我們要擴展到 k 倍 Context,就需要將 進制轉換為 進制,那么 應該滿足:
那么得到 。至于最高頻是 項,引入 變為 ,由于 d 很大,,所以它還是接近于初始值 ,等價于外推。 ? 所以這樣的方案簡單巧妙地將外推和內插結合了起來。另外,由于 d 比較大,因此 跟 差別不大,所以它跟前面基于進制思想提出的解 是基本一致的。還有,從提出者這個思想來看,任意能實現“高頻外推、低頻內插”的方案都是可以的,并非只有上述引入 的方案。 ? 如果從前面的進制轉換的角度分析,直接外推會將外推壓力集中在“高位(m 較大)”上,而位置內插則會將“低位(m 較小)”的表示變得更加稠密,不利于區分相對距離。而 NTK-aware Scaled RoPE 其實就是進制轉換,它將外推壓力平攤到每一位上,并且保持相鄰間隔不變,這些特性對明顯更傾向于依賴相對位置的 LLM 來說是非常友好和關鍵的,所以它可以不微調也能實現一定的效果。 ? 從公式(17)可以看出,cos,sin 事實上是一個整體,所以它實際只有 d/2 位,也就是說它相當于位置 n 的 d/2 位 進制。如果我們要擴展到 k 倍 Context,就需要將 進制轉換為 進制,那么 應該滿足: 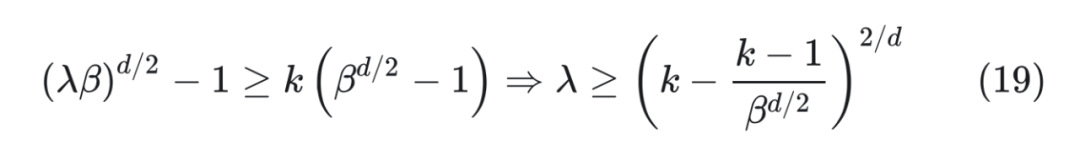 所以可以取 。 ? 于是新的 RoPE 變為:
所以可以取 。 ? 于是新的 RoPE 變為: 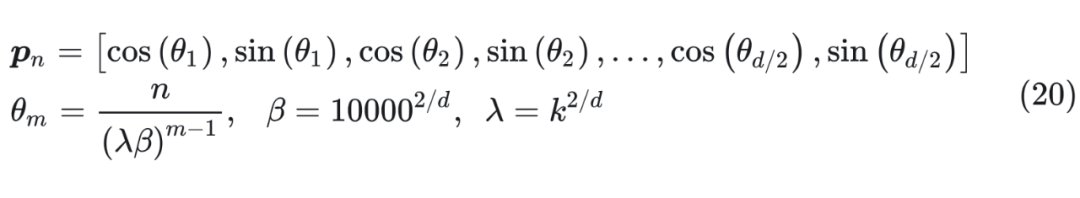 這樣就從 進制的思路解釋了 NTK-RoPE 的原理。 ? 下面我們看一下位置插值和 NTK-Aware Scaled RoPE 的實驗效果:
這樣就從 進制的思路解釋了 NTK-RoPE 的原理。 ? 下面我們看一下位置插值和 NTK-Aware Scaled RoPE 的實驗效果: 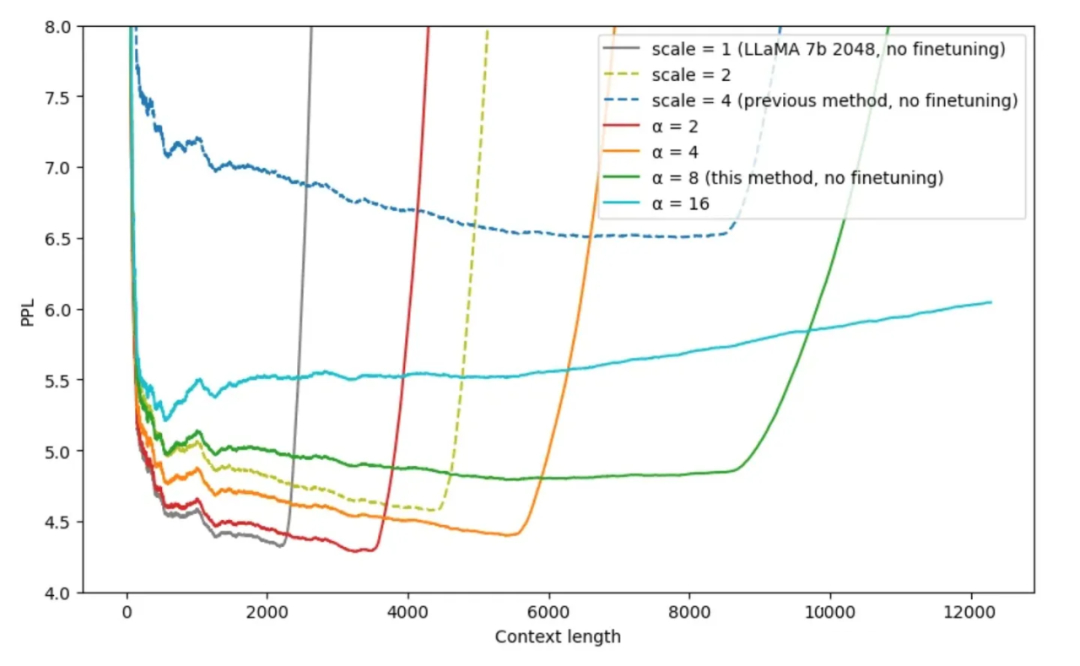
 電子發燒友App
電子發燒友App










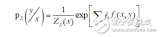


















評論