量化（Quantization）在加速神經網絡方面發揮了巨大作用——從 32 位到 16 位再到 8 位，甚至更快。它是如此重要，以至于谷歌目前因涉嫌侵犯 BF16 的創建者而被起訴，索賠 16 億至 52 億美元。所有的目光都集中在數字格式上，因為它們在過去十年中對人工智能硬件效率的提升起到了很大的作用。較低精度的數字格式有助于推倒數十億參數模型的內存墻。

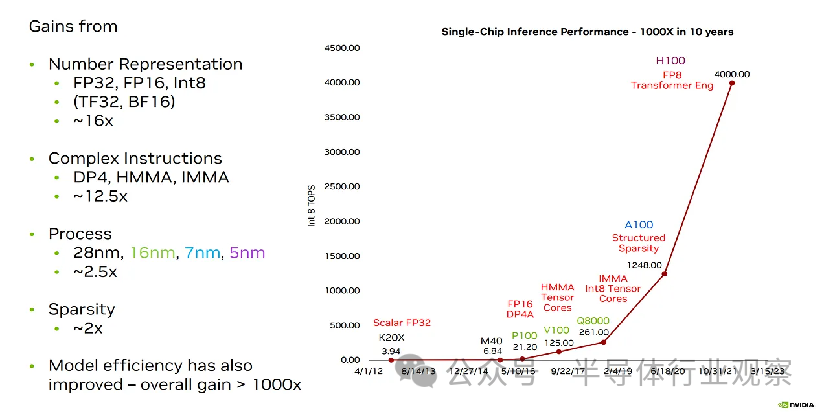
在本文中，我們將從基本原理的基礎上，從數字格式的基本原理到神經網絡量化的當前技術水平進行技術探討。我們將介紹浮點與整數、電路設計注意事項、塊浮點、MSFP、微縮放格式、對數系統等。我們還將介紹推理的量化和數字格式的差異以及高精度與低精度訓練方法。此外，我們將討論面臨量化和準確性損失相關挑戰的模型的下一步發展。

上述都是設計一顆AI芯片需要考量的因素。

01.?矩陣乘法

任何現代機器學習模型的大部分都是矩陣乘法。在GPT-3中，每一層都使用大量矩陣乘法：例如，其中一個具體運算是（2048 x 12288）矩陣乘以（12288 x 49152）矩陣，輸出（2048 x 49152）矩陣。

重要的是如何計算輸出矩陣中的每個單獨元素，這可以歸結為兩個非常大的向量的點積 - 在上面的示例中，大小為 12288。這由 12288 次乘法和 12277 次加法組成，它們累積成一個數字– 輸出矩陣的單個元素。

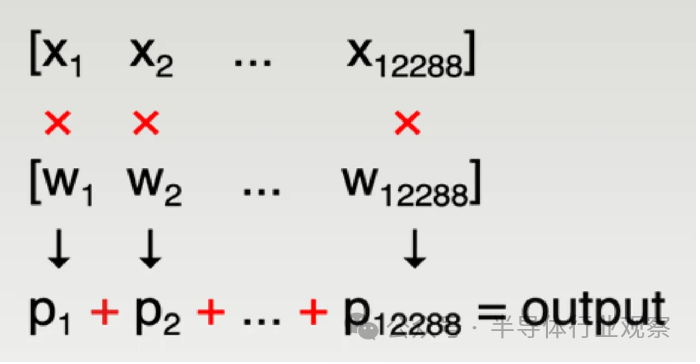
通常，這是通過將累加器寄存器初始化為零，然后重復地在硬件中完成的

乘以 x_i * w_i；

將其添加到累加器中；

每個周期的吞吐量均為 1。經過大約 12288 個循環后，輸出矩陣的單個元素的累加完成。這種“融合乘加”運算 (FMA：fused multiply-add) 是機器學習的基本計算單元：芯片上有數千個 FMA 單元戰略性地排列以有效地重用數據，因此可以并行計算輸出矩陣的許多元素，以減少所需的周期數。

上圖中的所有數字都需要在芯片內部的某個位以某種方式以位表示：

x_i，輸入激活；

w_i，權重；

p_i，成對乘積；

整個輸出完成累加之前的所有中間部分累加和；

最終輸出總和；

在這個巨大的設計空間中，當今大多數機器學習量化研究都可以歸結為兩個目標：

足夠準確地存儲數千億個權重，同時使用盡可能少的位，從容量和帶寬的角度減少內存占用。這取決于用于存儲權重的數字格式。

實現良好的能源和面積效率。這主要取決于用于權重和激活的數字格式；

這些目標有時是一致的，有時是不一致的——我們將深入研究這兩個目標。

02.?數字格式設計目標 1：芯片效率

許多機器學習芯片計算性能的根本限制是功耗。雖然 H100 理論上可以實現 2,000 TFLOPS 的計算能力，但在此之前它會遇到功率限制 - 因此每焦耳能量的 FLOPs 是一個非常需要跟蹤的指標。鑒于現代訓練運行現在經常超過 1e25 次flops，我們需要極其高效的芯片，在數月內吸收(sucking)兆瓦功率，才能擊敗?SOTA。 ?

03.?基本數字格式

首先，讓我們深入了解計算中最基本的數字格式：整數。 ? 一、以 2 為底的正整數 ? 正整數具有明顯的以 2 為底的表示形式。這些稱為 UINT，即無符號整數。以下是 8 位無符號整數（也稱為 UINT8，范圍從 0 到 255）的一些示例。 ?

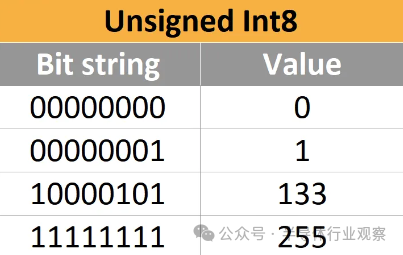
? 這些整數可以有任意位數，但通常僅支持以下四種格式：UINT8、UINT16、UINT32 和 UINT64。 ?

二、負整數（Negative integers）

負整數需要一個符號來區分正負。我們可以將一個指示符放在最高有效位中：例如0011 表示+3，1011 表示–3。這稱為符號-數值（sign-magnitude）表示。以下是 INT8 的一些示例，其范圍從 –128 到 127。請注意，由于第一位是符號，因此最大值實際上已從 255 減半到 127。 ? 符號-數值很直觀，但效率很低——您的電路必須實現截然不同的加法和減法算法，而這些算法又不同于沒有符號位的無符號整數的電路。有趣的是，硬件設計人員可以通過使用二進制補碼表示來解決這個問題，這使得可以對正數、負數和無符號數使用完全相同的進位加法器電路。所有現代 CPU 都使用二進制補碼。 ? 在 unsigned int8 中，最大數字 255 是 11111111。如果添加數字 1，255 會溢出到 00000000，即 0。在signed int8 中，最小數字是 -128，最大數字是 127。作為讓 INT8 和 UINT8 共享硬件的技巧資源，-1可以用11111111表示。現在當數字加1時，它溢出到00000000，按預期表示0。同樣，11111110 可以表示為-2。 ?

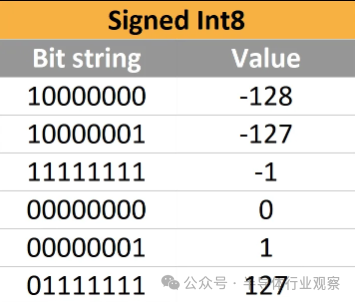
? 溢出被用作一個功能！實際上，0 到 127 被映射為正常值，128 到 255 被直接映射到 -128 到 -1。

04.?固定點（Fixed Point）

為了更進一步，我們可以在現有硬件上輕松創建新的數字格式，而無需進行修改。雖然這些都是整數，但您可以簡單地想象它們是其他東西的倍數！例如，0.025 只是千分之 25，它可以存儲為整數 25。現在我們只需要記住其他地方使用的所有數字都是千分之幾。 ? 新的“數字格式”可以表示從 –0.128 到 0.127 的千分之一的數字，而沒有實際的邏輯變化。完整的數字仍被視為整數，然后小數點固定在右起第三位。這種策略稱為定點（ fixed point）。 ? 更一般地說，這是一個有用的策略，我們將在本文中多次回顧它 - 如果您想更改可以表示的數字范圍，請在某處添加比例因子。（顯然，您可以用二進制來執行此操作，但十進制更容易討論）。

05.?浮點（Floating Point）

但定點有一些缺點，特別是對于乘法。假設您需要計算一萬億乘以一萬億分——尺寸上的巨大差異就是高*動態范圍*的一個例子。那么 1012和 10-12都必須用我們的數字格式來表示，所以很容易計算出你需要多少位：從 0 到 1 萬億以萬億分之一的增量計數，你需要 10^24 增量，log2(10^ 24) ~= 80 位來表示具有我們想要的精度級別的動態范圍。 ? 每個數字 80 位顯然是相當浪費的。您不一定關心絕對精度，您關心相對精度。因此，盡管上述格式能夠準確區分 1 萬億和 999,999,999,999.999999999999，但您通常不需要這樣做。大多數時候，您關心的是相對于數字大小的誤差量。 ? 這正是科學記數法所解決的問題：在前面的示例中，我們可以將一萬億寫為 1.00 * 10^12，將一萬億寫為 1.00 * 10^-12，這樣的存儲空間要少得多。這更復雜，但可以讓您在相同的上下文中表示極大和極小的數字，而無需擔心。 ? 因此，除了符號和值之外，我們現在還有一個指數。IEEE 754-1985 標準化了行業范圍內以二進制存儲該數據的方式，而當時使用的格式略有不同。主要有趣的格式，32 位浮點數（“float32”或“FP32”）可描述為 (1,8,23)：1 個符號位、8 個指數位和 23 個尾數位。 ?

符號位為0表示正，1表示負；

指數位被解釋為無符號整數 e，并表示比例因子 2 e-127，其值可以介于 2-126-和2127之間。更多指數位意味著更大的動態范圍；

尾數位表示值 1.。更多尾數位意味著更高的相對精度；

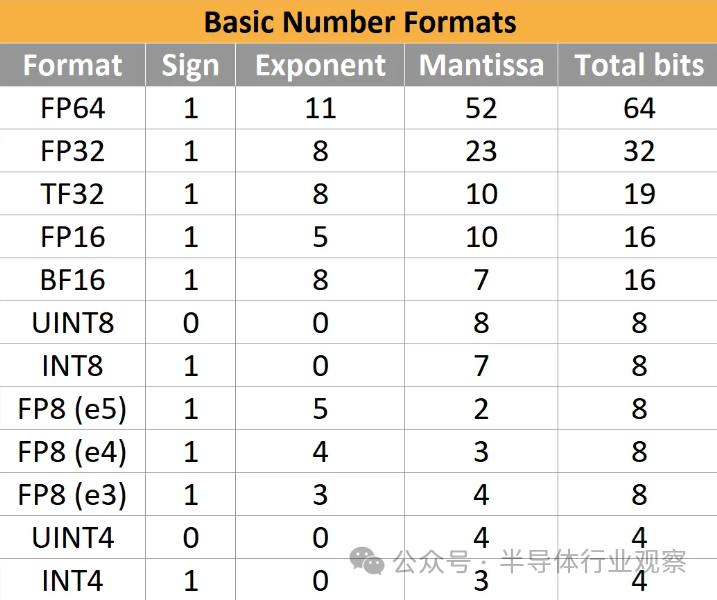
? 其他位寬已標準化或事實上已采用，例如 FP16 (1,5,10) 和 BF16 (1,8,7)。爭論的焦點是范圍與精度。 ?

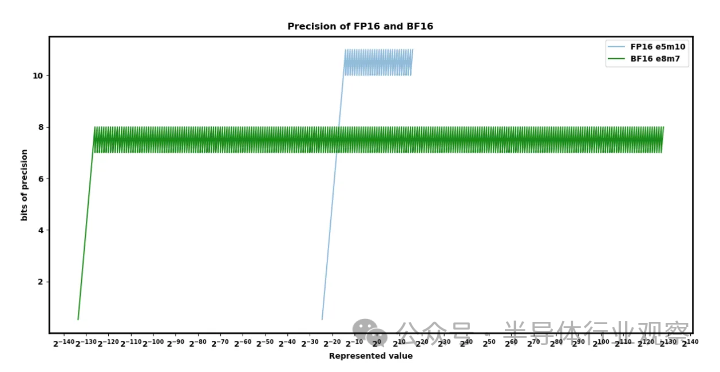
? FP8（1,5,2 或 1,4,3）最近在 OCP 標準中標準化了一些額外的怪癖，但目前還沒有定論。許多人工智能硬件公司已經實現了具有稍微優越的變體的芯片，這些變體與標準不兼容。

06.?硅效率（Silicon Efficiency）

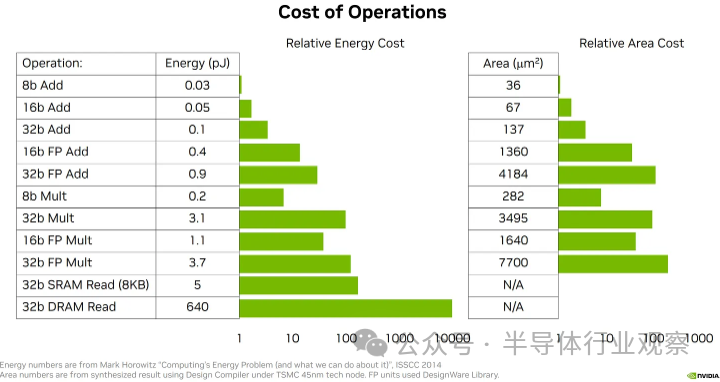
回到硬件效率，所使用的數字格式對硅面積和所需功率有巨大影響。 ?

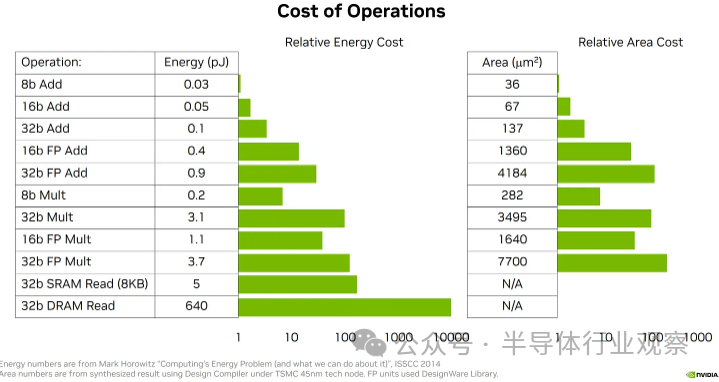
? 一、整數硅設計電路（Integer Silicon Design Circuit）

整數加法器是有史以來研究最深入的硅設計問題之一。雖然實際的實現要復雜得多，但考慮加法器的一種方法是將它們想象為根據需要將 1 一直相加并一直加到總和上，因此在某種意義上，n 位加法器正在做一定量的工作到 n ? 對于乘法，請回想一下小學的長乘法。我們進行 n 位乘以 1 位的乘積，然后最后將所有結果相加。在二進制中，乘以 1 位數字很簡單（0 或 1）。這意味著 n 位乘法器本質上由 n 位加法器的 n 次重復組成，因此工作量與 n^2 成正比。 ? 雖然實際實現因面積、功率和頻率限制而有很大不同，但通常 1) 乘法器比加法器昂貴得多，但 2) 在低位數（8 位及以下）時，FMA 的功耗和面積成本更高以及來自加法器的更多相對貢獻((n 與 n^2 縮放).

? 二、浮點電路(Floating Point Circuits)

浮點單位有很大不同。相反，乘積/乘法相對簡單。 ? 如果恰好有一個輸入符號為負，則符號為負，否則為正。 指數是傳入指數的整數和。 尾數是傳入尾數的整數積。 ? 相比之下，總和相當復雜。 ? 首先，計算指數差。（假設 exp1 至少與 exp2 一樣大 - 如果沒有，請在說明中交換它們）； 將尾數 2 向下移動 (exp1 - exp2)，使其與尾數 1 對齊； 向每個尾數添加隱式前導 1。如果一個符號為負，則對尾數之一執行二進制補碼； 將尾數加在一起形成輸出尾數； 如果發生溢出，則結果指數加1，尾數下移； 如果結果為負，則將其轉換回無符號尾數并將輸出符號設置為負； 對尾數進行歸一化，使其具有前導 1，然后刪除隱式前導 1； 適當舍入尾數（通常舍入到最接近的偶數）； ? 值得注意的是，浮點乘法的成本甚至比整數乘法“更少”，因為尾數乘積中的位數更少，而指數的加法器比乘法器小得多，幾乎無關緊要。 ? 顯然，這也是極其簡化的，特別是我們沒有討論的非正規和 nan 處理占用了大量的空間。但要點是，在低位數浮點中，乘積很便宜，而累加則很昂貴。 ?

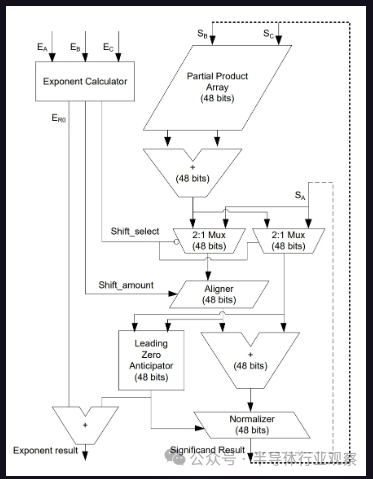
? 我們提到的所有部分在這里都非常明顯 - 將指數相加，尾數的大型乘法器數組，根據需要移動和對齊事物，然后標準化。（從技術上講，真正的“融合”（“fused”）乘加有點不同，但我們在這里省略了。） ?

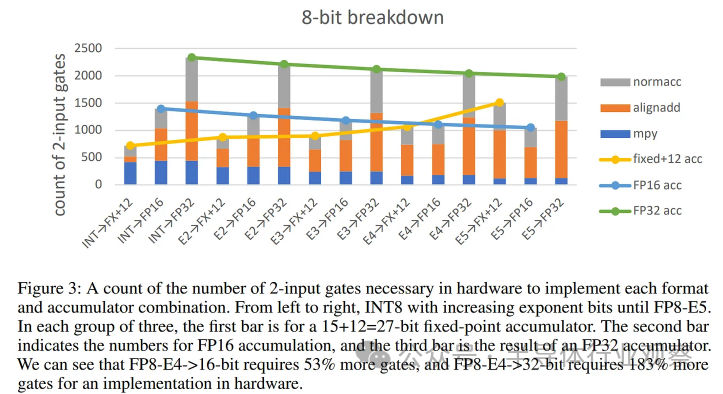
? 該圖表說明了上述所有要點。有很多東西需要消化，但要點是 INT8 x INT8 的累加和累加到定點 (FX) 的成本是最便宜的，并且由乘法 (“mpy”) 主導，而使用浮點作為操作數或累加格式（通常在很大程度上）由累積成本（“alignadd”+“normacc”）主導。例如，通過使用帶有“定點”累加器的 FP8 操作數而不是通常的 FP32，可以節省大量成本。 ? 總而言之，本文和其他論文聲稱 FP8 FMA 將比 INT8 FMA 多占用 40-50% 的硅面積，并且能源消耗同樣更高或更差的說法一直。這是大多數專用 ML 推理芯片使用 INT8 的主要原因。

07.?數字格式設計目標 2：準確性

既然整數總是更便宜，為什么我們不到處使用 INT8 和 INT16 而不是 FP8 和 FP16呢？這取決于這些格式能夠如何準確地表示神經網絡中實際顯示的數字。 ? 我們可以將每種數字格式視為一個查找表。例如，一個非常愚蠢的 2 位數字格式可能如下所示： ?

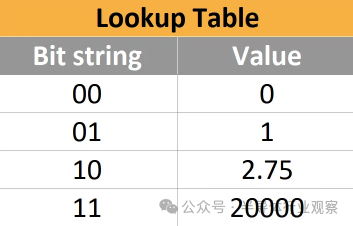
? 顯然，這組四個數字對任何事情都沒有多大用處，因為它缺少太多數字 - 事實上，根本沒有負數。如果表中不存在神經網絡中的數字，那么您所能做的就是將其四舍五入到最近的條目，這會給神經網絡帶來一點誤差。 ? 那么表中理想的值集是多少？表的大小可以有多小？ ? 例如，如果神經網絡中的大多數值都接近于零（實際上也是如此），我們希望能夠有很多這些數字接近于零，這樣我們就可以通過犧牲準確性來獲得更高的準確性。哪里沒有。 ? 在實踐中，神經網絡通常是正態分布或拉普拉斯分布，有時根據模型架構的確切數值，存在大量異常值。特別是，對于非常大的語言模型， 往往會出現極端異常值，這些異常值很少見，但對模型的功能很重要。

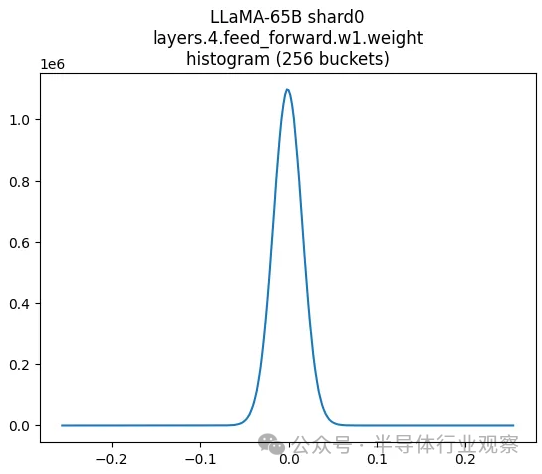
? 上圖顯示了 LLAMA 65B 部分權重。這看起來很像正態分布。如果將此與 FP8 和 INT8 中的數字分布進行比較，很明顯浮點集中在重要的地方 - 接近零。這就是我們使用它的原因！ ?

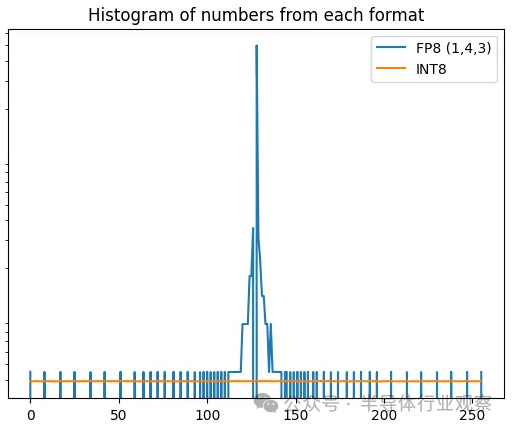
? 不過，它仍然與真實分布不太匹配——每次指數遞增時，它仍然有點太尖了，但比 int8 好得多。 ? 我們可以做得更好嗎？從頭開始設計格式的一種方法是最小化平均絕對誤差——舍入造成的平均損失量。

08.?對數系統（Log Number Systems）

例如， Nvidia在HotChips?上宣稱 Log Number System 是繼續擴展過去 8 位數字格式的可能途徑。使用對數系統時，舍入誤差通常較小，但存在許多問題，包括極其昂貴的加法器。 ?

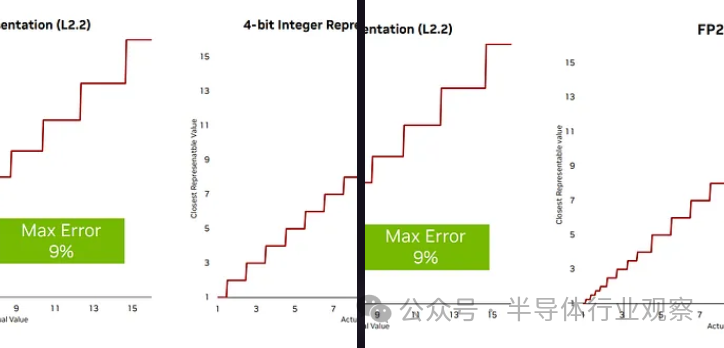
? NF4 和變體 (AF4) 是 4 位格式，假設權重遵循完全正態分布，則使用精確的查找表來最大限度地減少誤差。但這種方法在面積和功耗方面非常昂貴——現在每個操作都需要查找巨大的條目表，這比任何 INT/FP 操作都要糟糕得多。 ? 存在多種替代格式：posits、ELMA、PAL 等。這些技術聲稱在計算效率或表示準確性方面具有多種優勢，但尚未達到商業相關規模。也許其中之一，或者尚未發表/發現的一個，將具有 INT 的成本和 FP 的表征準確性——一些人已經做出了這樣的聲明，或者更好。 ? 我們個人對 Lemurian Labs PAL 最有希望，但關于其數字格式，還有很多信息尚未披露。他們聲稱其 16 位精度和范圍比 FP16 和 BF16 更好，同時硬件也更便宜。 ?

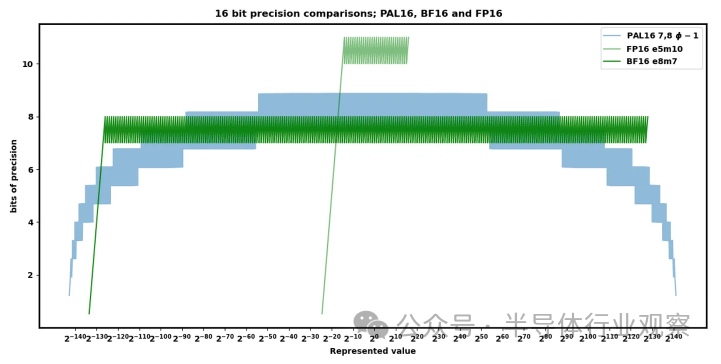
? 隨著我們繼續擴展到過去的 8 位格式，PAL4 還聲稱比 HotChips 上的 Nvidia 等對數系統有更好的分布。他們的紙面聲明令人驚嘆，但目前還沒有硬件實現該格式。 ?

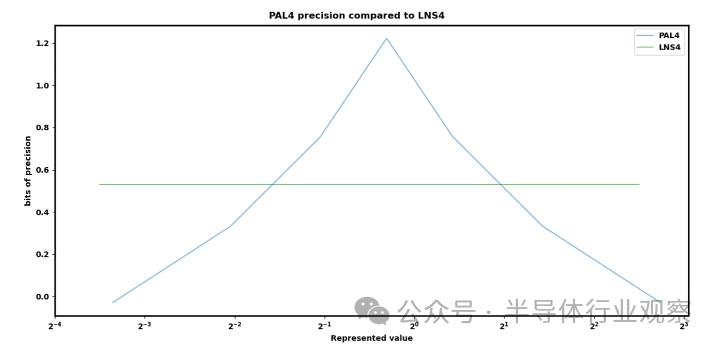
09.?塊號格式（Block Number Formats)

一個有趣的觀察是，元素的大小幾乎總是與張量中附近的元素相似。當張量的元素比平常大得多時，附近的元素本質上并不重要——它們相對太小，無法在點積中看到。 ? 我們可以利用這一點 - 我們可以在多個元素之間共享一個指數，而不是對每個數字都使用浮點指數。這節省了很多大部分冗余的指數。 ? 這種方法已經存在了一段時間 - Nervana Flexpoint、Microsoft MSFP12、Nvidia VSQ - 直到 2023 年 OCP 的 Microscaling 才出現。 ? 此時，存在一整套可能的格式，具有不同的權衡。微軟試圖量化硬件的設計空間： ?

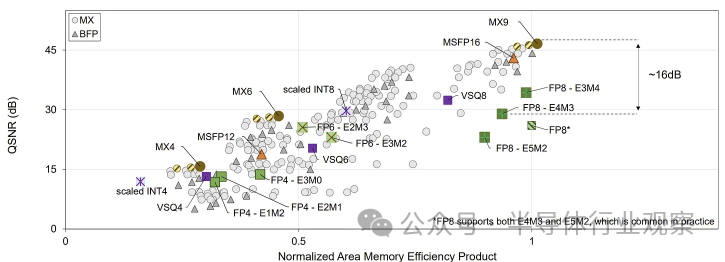
? 硬件供應商面臨著一個棘手的問題，即嘗試設計高度專業化的高效格式，同時又不關閉可能具有截然不同的數值分布的未來模型架構的大門。

10.?推理(Inference)

上述大部分內容都適用于推理和訓練，但每種都有一些特定的復雜性。 ? 推理對成本/功耗特別敏感，因為模型通常只訓練一次，但部署到數百萬客戶。訓練也更加復雜，有許多數值上有問題的操作（見下文）。這意味著推理芯片在采用更小、更便宜的數字格式方面通常遠遠領先于訓練芯片，因此模型訓練的格式和模型推理的格式之間可能會出現很大的差距。 ? 有許多工具可以從一種格式適應另一種格式，這些工具屬于一個范圍： ? 一方面，訓練后量化（PTQ:post-training quantization）不需要執行任何實際的訓練步驟，只需根據一些簡單的算法更新權重： ? 最簡單的方法是將每個權重四舍五入到最接近的值。

The easiest is to simply round each weight to the nearest value. ? LLM.int8() 將除一小部分以外的所有異常值權重轉換為 INT8; GPTQ 使用有關權重矩陣的二階信息來更好地量化; Smoothquant 進行數學上等效的變換，嘗試平滑激活異常值; AWQ 使用有關激活的信息來更準確地量化最顯著的權重; QuIP 對模型權重進行預處理，使其對量化不太敏感; AdaRound 將每一層的舍入分別優化為二次二元優化; ? 存在許多其他方法并且正在不斷發布。許多“訓練后”量化方法通過使用某種修改后的訓練步驟或代理目標迭代優化量化模型，從而模糊了與訓練的界限。這里的關鍵方面是，這些極大地降低了成本，但現實世界的性能損失通常比人們經常吹捧的簡單基準要大。 ?

另一方面，量化感知訓練 (QAT:quantization-aware training) 會改變精度并繼續訓練一段時間以使模型適應新的精度。所有量化方法都應至少部分使用此機制，以在現實世界性能中實現最小的精度損失。這直接使用常規訓練過程來使模型適應量化機制，通常被認為更有效，但計算成本更高。

11.?訓練(Training)

由于向后傳遞，訓練稍微復雜一些。有 3 個 matmul——一個在前向傳遞中，兩個在后向傳遞中。 ?

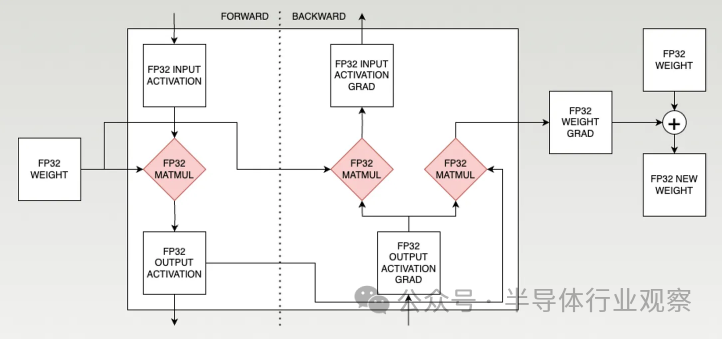
? 每個訓練步驟最終都會接收權重，對各種數據進行一系列矩陣乘法，并產生新的權重。 ? FP8 訓練更加復雜。下面是 Nvidia FP8 訓練方法的稍微簡化版本。 ?

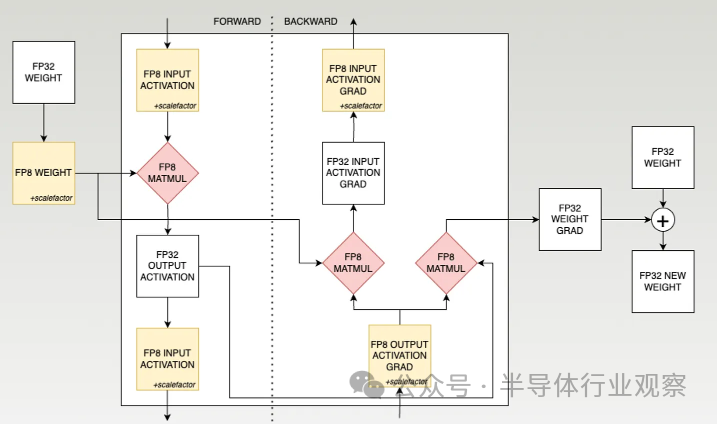
? 這個清單的一些顯著特點： ? 每個 matmul 都是 FP8 x FP8 并累加為 FP32 （實際上精度較低，但 Nvidia 告訴大家它是 FP32），然后量化為 FP8 以用于下一層。累加必須比 FP8 具有更高的精度，因為它涉及對同一大型累加器進行數萬次連續的小更新，因此每個小更新需要很高的精度才能不向下舍入為零； ? 每個 FP8 權重張量都帶有一個比例因子。由于每一層的范圍可能顯著不同，因此縮放每個張量以適應該層的范圍至關重要； ? 權重更新（在主框之外）對精度非常敏感，并且通常保持較高的精度（通常為 FP32）。這又歸結為幅度不匹配——權重更新與權重相比很小，因此再次需要精度才能使更新不向下舍入為零； ? 最后，訓練與推理的一大區別是梯度有更多的極端異常值，這一點非常重要。可以將激活梯度（例如 SwitchBack、AQT）量化為 INT8，但權重梯度迄今為止抵制了這種努力，必須保留在 FP16 或 FP8 (1,5,2) 中。

審核編輯：黃飛

?