作者：「報(bào)告，今天也有好好學(xué)習(xí)」

導(dǎo)讀

本篇文章，用一種通俗易懂的方式來(lái)介紹機(jī)器學(xué)習(xí)的理論基礎(chǔ)，是入門(mén)機(jī)器學(xué)習(xí)不可錯(cuò)過(guò)的文章。

在這里，我要先引用一下一個(gè)非常經(jīng)典的小故事，幫助大家更清楚地理解機(jī)器學(xué)習(xí)。

在一個(gè)酒吧里，吧臺(tái)上擺著十杯幾乎一樣的紅酒，老板跟你打趣說(shuō)想不想來(lái)玩?zhèn)€游戲，贏(yíng)了免費(fèi)喝酒，輸了付3倍酒錢(qián)，那么贏(yíng)的概率是多少？

你是個(gè)愛(ài)冒險(xiǎn)的人，果斷說(shuō)玩！

老板接著道：你眼前的這十杯紅酒，每杯略不相同，前五杯屬于「赤霞珠」后五杯屬于「黑皮諾」。現(xiàn)在，我重新倒一杯酒，你只需要正確地告訴我它屬于哪一類(lèi)。

聽(tīng)完你有點(diǎn)心虛：根本不懂酒啊，光靠看和嘗根本區(qū)分辨不出來(lái)，不過(guò)想起自己是搞機(jī)器學(xué)習(xí)的，不由多了幾分底氣爽快地答應(yīng)了老板！

你沒(méi)有急著品酒而是問(wèn)了老板每杯酒的一些具體信息：酒精濃度、顏色深度，以及一份紙筆， 老板一邊倒一杯新酒，你邊瘋狂打草稿。

很快，你告訴老板這杯新酒應(yīng)該是「赤霞珠」。

老板瞪大了眼下巴也差點(diǎn)驚掉，從來(lái)沒(méi)有人一口酒都不嘗就能答對(duì)，無(wú)數(shù)人都是反復(fù)嘗來(lái)嘗去，最后以猶豫不定猜錯(cuò)而結(jié)束。

你神秘地笑了笑，老板信守承諾讓你開(kāi)懷暢飲。微醺之時(shí)，老板終于忍不住湊向你打探是怎么做到的。

你炫耀道:無(wú)他，但機(jī)器學(xué)習(xí)熟爾。

老板：…

怎么辨別出來(lái)的呢？

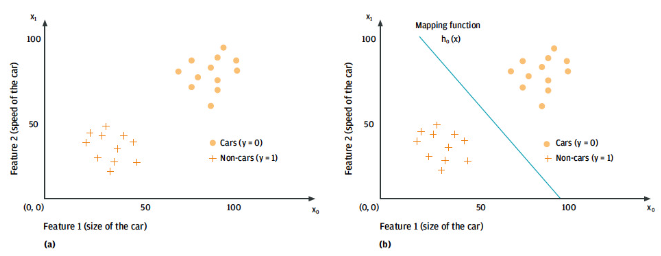
如下圖，故事中的你畫(huà)了類(lèi)似這樣子的圖，就區(qū)分出來(lái)了

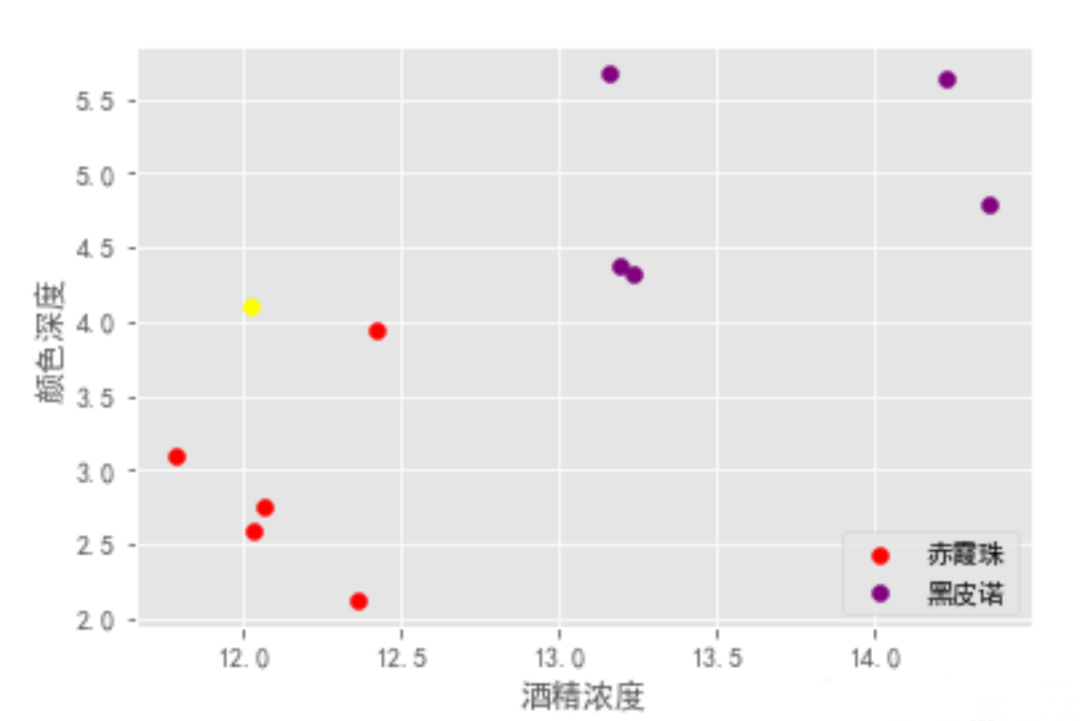
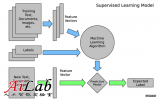
有監(jiān)督學(xué)習(xí)

指對(duì)數(shù)據(jù)的若干特征與若干標(biāo)簽(類(lèi)型)之間的關(guān)聯(lián)性進(jìn)行建模的過(guò)程。只要模型被確定，就可以應(yīng)用到新的未知數(shù)據(jù)上。

這類(lèi)學(xué)習(xí)過(guò)程可以進(jìn)一步分為「分類(lèi)」(classification)任務(wù)和「回歸」(regression)任務(wù)。

在分類(lèi)任務(wù)中，標(biāo)簽都是離散值。

而在回歸任務(wù)中，標(biāo)簽都是連續(xù)值。

無(wú)監(jiān)督學(xué)習(xí)?

指對(duì)不帶任何標(biāo)簽的數(shù)據(jù)特征進(jìn)行建模，通常被看成是一種“讓數(shù)據(jù)自己介紹自己” 的過(guò)程。

這類(lèi)模型包括「聚類(lèi)」(clustering)任務(wù)和「降維」(dimensionality reduction)任務(wù)。

聚類(lèi)算法可以將數(shù)據(jù)分成不同的組別，而降維算法追求用更簡(jiǎn)潔的方式表現(xiàn)數(shù)據(jù)。

半監(jiān)督學(xué)習(xí)?

另外，還有一種半監(jiān)督學(xué)習(xí)(semi-supervised learning)方法，介于有監(jiān)督學(xué)習(xí)和無(wú)監(jiān)督學(xué)習(xí)之間。通常可以在數(shù)據(jù)不完整時(shí)使用。

強(qiáng)化學(xué)習(xí)?

強(qiáng)化學(xué)習(xí)不同于監(jiān)督學(xué)習(xí)，它將學(xué)習(xí)看作是試探評(píng)價(jià)過(guò)程，以"試錯(cuò)" 的方式進(jìn)行學(xué)習(xí)，并與環(huán)境進(jìn)行交互已獲得獎(jiǎng)懲指導(dǎo)行為，以其作為評(píng)價(jià)。

此時(shí)系統(tǒng)靠自身的狀態(tài)和動(dòng)作進(jìn)行學(xué)習(xí)，從而改進(jìn)行動(dòng)方案以適應(yīng)環(huán)境。

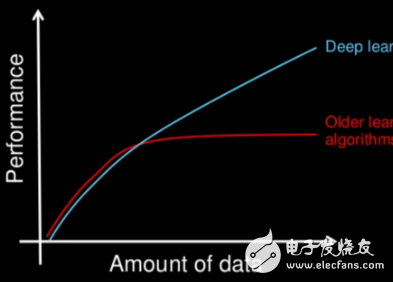
（提示：半監(jiān)督學(xué)習(xí)和強(qiáng)化學(xué)習(xí)比較偏向于深度學(xué)習(xí)）

輸入/輸出空間、特征空間?

在上面的場(chǎng)景中，每一杯酒稱(chēng)作一個(gè)「樣本」，十杯酒組成一個(gè)樣本集。

酒精濃度、顏色深度等信息稱(chēng)作「特征」。這十杯酒分布在一個(gè)「多維特征空間」中。

進(jìn)入當(dāng)前程序的“學(xué)習(xí)系統(tǒng)”的所有樣本稱(chēng)作「輸入」，并組成「輸入空間」。

在學(xué)習(xí)過(guò)程中，所產(chǎn)生的隨機(jī)變量的取值，稱(chēng)作「輸出」，并組成「輸出空間」。

在有監(jiān)督學(xué)習(xí)過(guò)程中，當(dāng)輸出變量均為連續(xù)變量時(shí)，預(yù)測(cè)問(wèn)題稱(chēng)為回歸問(wèn)題；當(dāng)輸出變量為有限個(gè)離散變量時(shí)，預(yù)測(cè)問(wèn)題稱(chēng)為分類(lèi)問(wèn)題。

過(guò)擬合與欠擬合?

先來(lái)一句易懂的話(huà)：

過(guò)擬合簡(jiǎn)單來(lái)說(shuō)就是模型把訓(xùn)練集的東西學(xué)得太精了，對(duì)未知的數(shù)據(jù)效果卻很差（打個(gè)比方就是考前你練得很不錯(cuò)，給啥做過(guò)的題都說(shuō)得出答案，但是考試的時(shí)候碰到新題了就做得很差）

欠擬合就是模型學(xué)得很差，打個(gè)比方就是考前有題給你練，你也練了，但就是練不會(huì)，學(xué)不懂。

下面是具體介紹：

當(dāng)假設(shè)空間中含有不同復(fù)雜度的模型時(shí)，就要面臨模型選擇(model selection)的問(wèn)題。

我們希望獲得的是在新樣本上能表現(xiàn)得很好的學(xué)習(xí)器。為了達(dá)到這個(gè)目的，我們應(yīng)該從訓(xùn)練樣本中盡可能學(xué)到適用于所有潛在樣本的"普遍規(guī)律"

我們認(rèn)為假設(shè)空間存在這種"真"模型，那么所選擇的模型應(yīng)該逼近真模型。

擬合度可簡(jiǎn)單理解為模型對(duì)于數(shù)據(jù)集背后客觀(guān)規(guī)律的掌握程度，模型對(duì)于給定數(shù)據(jù)集如果擬合度較差，則對(duì)規(guī)律的捕捉不完全，用作分類(lèi)和預(yù)測(cè)時(shí)可能準(zhǔn)確率不高。

換句話(huà)說(shuō)，當(dāng)模型把訓(xùn)練樣本學(xué)得太好了的時(shí)候，很可能已經(jīng)把訓(xùn)練樣本自身的一些特點(diǎn)當(dāng)作了所有潛在樣本的普遍性質(zhì)，這時(shí)候所選的模型的復(fù)雜度往往會(huì)比真模型更高，這樣就會(huì)導(dǎo)致泛化性能下降。這種現(xiàn)象稱(chēng)為過(guò)擬合(overfitting)。可以說(shuō)，模型選擇旨在避免過(guò)擬合并提高模型的預(yù)測(cè)能力。

與過(guò)擬合相對(duì)的是欠擬合(underfitting)，是指模型學(xué)習(xí)能力低下，導(dǎo)致對(duì)訓(xùn)練樣本的一般性質(zhì)尚未學(xué)好。

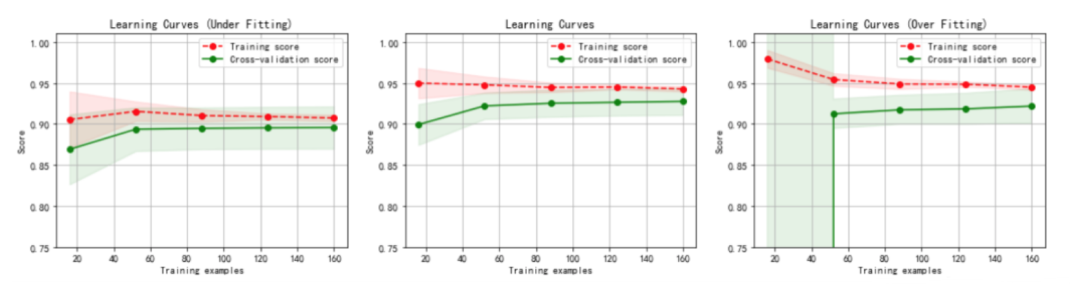
虛線(xiàn)：針對(duì)訓(xùn)練數(shù)據(jù)集計(jì)算出來(lái)的分?jǐn)?shù)，即針對(duì)訓(xùn)練數(shù)據(jù)集擬合的準(zhǔn)確性。

實(shí)線(xiàn)：針對(duì)交叉驗(yàn)證數(shù)據(jù)集計(jì)算出來(lái)的分?jǐn)?shù)，即針對(duì)交叉驗(yàn)證數(shù)據(jù)集預(yù)測(cè)的準(zhǔn)確性。

1.左圖：一階多項(xiàng)式，欠擬合.

訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性（虛線(xiàn)）和交叉驗(yàn)證數(shù)據(jù)集的準(zhǔn)確性（實(shí)線(xiàn)）靠得很近，總體水平比較高。

隨著訓(xùn)練數(shù)據(jù)集的增加，交叉驗(yàn)證數(shù)據(jù)集的準(zhǔn)確性(實(shí)線(xiàn))逐漸增大，逐漸和訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性(虛線(xiàn))靠近，但其總體水平比較低，收斂在 0.88 左右。

訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性也比較低，收斂在 0.90 左右。

當(dāng)發(fā)生高偏差時(shí)，增加訓(xùn)練樣本數(shù)量不會(huì)對(duì)算法準(zhǔn)確性有較大的改善。

2.中圖：三階多項(xiàng)式，較好地?cái)M合了數(shù)據(jù)集.

訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性（虛線(xiàn)）和交叉驗(yàn)證數(shù)據(jù)集的準(zhǔn)確性（實(shí)線(xiàn)）靠得很近，總體水平比較高。

3.右圖：十階多項(xiàng)式，過(guò)擬合。

隨著訓(xùn)練數(shù)據(jù)集的增加，交叉驗(yàn)證數(shù)據(jù)集的準(zhǔn)確性(實(shí)線(xiàn))也在增加，逐漸和訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性 (虛線(xiàn))靠近，但兩者之間的間隙比較大。

訓(xùn)練數(shù)據(jù)集的準(zhǔn)確性很高，收斂在 0.95 左右。

交叉驗(yàn)證數(shù)據(jù)集的準(zhǔn)確性值卻較低，最終收斂在 0.91 左右。

從圖中我們可以看出，對(duì)于復(fù)雜數(shù)據(jù)，低階多項(xiàng)式往往是欠擬合的狀態(tài)，而高階多項(xiàng)式則過(guò)分捕捉噪聲數(shù)據(jù)的分布規(guī)律，而噪聲之所以稱(chēng)為噪聲，是因?yàn)槠浞植己翢o(wú)規(guī)律可言，或者其分布毫無(wú)價(jià)值，因此就算高階多項(xiàng)式在當(dāng)前訓(xùn)練集上擬合度很高，但其捕捉到的無(wú)用規(guī)律無(wú)法推廣到新的數(shù)據(jù)集上。因此該模型在測(cè)試數(shù)據(jù)集上執(zhí)行過(guò)程將會(huì)有很大誤差，即模型訓(xùn)練誤差很小，但泛化誤差很大。

審核編輯：黃飛