論文名稱(chēng)：Towards Generalizable and Faithful Logic Reasoning over Natural Language via Resolution Refutation

論文作者：孫洲浩，丁效*，杜理，蔡碧波，高靖龍，劉挺，秦兵 ?

1 引言

基于自然語(yǔ)言的邏輯推理任務(wù)需要模型理解自然語(yǔ)言聲明（statements）之間的抽象邏輯關(guān)系并推理出假設(shè)的真值（標(biāo)簽）。這類(lèi)任務(wù)正在越來(lái)越受到關(guān)注，因?yàn)樗鼘⒆匀徽Z(yǔ)言與抽象邏輯思維聯(lián)系起來(lái)，抽象邏輯思維在解決復(fù)雜問(wèn)題和認(rèn)知推理中發(fā)揮著關(guān)鍵作用。然而，這類(lèi)任務(wù)對(duì)于LLM來(lái)說(shuō)仍然較為困難，這是因?yàn)長(zhǎng)LM存在幻覺(jué)問(wèn)題，其在推理過(guò)程中可能會(huì)產(chǎn)生不正確的中間推理步驟，從而最終導(dǎo)致錯(cuò)誤的推理結(jié)果，因此是不可靠的。同時(shí)，如果將LLM看作一個(gè)推理系統(tǒng)，那么幻覺(jué)會(huì)影響這個(gè)系統(tǒng)的完備性。如果一個(gè)推理系統(tǒng)是完備的，那么我們可以通過(guò)應(yīng)用推理系統(tǒng)中包含的合法推理規(guī)則來(lái)推理出具有確定標(biāo)簽（True和False）的所有假設(shè)。然而，幻覺(jué)會(huì)阻止LLM通過(guò)運(yùn)用合法的推理規(guī)則得出結(jié)論，從而導(dǎo)致推理系統(tǒng)不完備。

為了減少幻覺(jué)從而提升忠實(shí)性，前人提出了分步推理方法，這些分步推理方法是基于前向鏈或后向鏈進(jìn)行設(shè)計(jì)的。基于前向鏈的方法從已知規(guī)則開(kāi)始，檢查是否存在某一個(gè)規(guī)則其所有的前提條件都被給定的事實(shí)所滿足，如果存在，則應(yīng)用前向鏈的推理規(guī)則來(lái)推導(dǎo)出新的結(jié)論，這個(gè)過(guò)程一直持續(xù)直到不能得出新的結(jié)論或假設(shè)已經(jīng)被證明。基于后向鏈的方法從假設(shè)開(kāi)始以相反的方向進(jìn)行推理，從而得出一組需要滿足的事實(shí)，然后檢查這些事實(shí)是否已經(jīng)被已知事實(shí)所滿足。通過(guò)引入了中間推理步驟，基于LLM的推理系統(tǒng)的忠實(shí)性得到了提升。

然而這些基于前向鏈或后向鏈的分步推理方法在復(fù)雜的邏輯推理場(chǎng)景下依然不盡如人意。在某些場(chǎng)景下，這些方法的性能可能會(huì)低于單獨(dú)使用LLMs，甚至低于隨機(jī)猜測(cè)（random guess）。這是因?yàn)榛谇跋蜴溁蚝笙蜴湹姆植酵评矸椒ㄊ遣煌陚涞摹＿@意味著一些具有確定標(biāo)簽的假設(shè)被模型會(huì)被認(rèn)為是Unknown。因此，它只能適應(yīng)于相對(duì)簡(jiǎn)單的推理場(chǎng)景。以前向鏈為例，前向鏈?zhǔn)遣煌陚涞囊驗(yàn)樗?dāng)且僅當(dāng)“某個(gè)規(guī)則的所有條件都可以被已知事實(shí)證明是真的”（條件1）時(shí)才能夠推理。然而，在推理過(guò)程中也存在一些特殊情況，前向鏈無(wú)法推理。對(duì)于圖1中的假設(shè)1，前向鏈無(wú)法推理出假設(shè)是正確的（True），因?yàn)橐?guī)則中包含的“kind people”這一條件無(wú)法被已知事實(shí)證明是真的。因此，我們無(wú)法得出任何推論，假設(shè)1將被視為Unknown。類(lèi)似地，對(duì)于后向鏈，假設(shè)1“not kind”沒(méi)有出現(xiàn)在規(guī)則的右側(cè)因此也無(wú)法進(jìn)行推理，該假設(shè)也將被視為Unknown。

圖1：基于自然語(yǔ)言的邏輯推理問(wèn)題樣例

受邏輯符號(hào)領(lǐng)域的邏輯推理方法的啟發(fā)，我們引入了一個(gè)在一階邏輯下完備的邏輯推理范式歸結(jié)反演（其推理過(guò)程不會(huì)受到條件1的約束）來(lái)提高完備性，并提出一個(gè)新的推理框架GFaiR。圖2展示了歸結(jié)反演的推理過(guò)程。對(duì)于圖1中的問(wèn)題，通過(guò)利用歸結(jié)的推理規(guī)則，GFaiR可以在自然語(yǔ)言水平上進(jìn)行歸結(jié)，從已知信息中逐步推導(dǎo)出“Everyone is not kind”。然后通過(guò)反演，“Bob is kind”出現(xiàn)在了已知信息中，進(jìn)而我們能夠推導(dǎo)出一個(gè)矛盾（Everyone is?not kind 與?Bob is kind兩者互相矛盾），從而證明假設(shè)1是真的。因此，歸結(jié)反演的結(jié)合使LLM能夠處理更復(fù)雜的邏輯推理場(chǎng)景，從而增強(qiáng)了泛化能力。

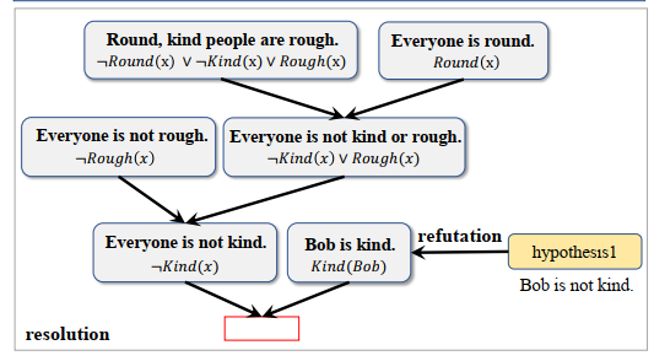
圖2：圖1問(wèn)題樣例的歸結(jié)反演推理過(guò)程

實(shí)驗(yàn)結(jié)果表明，我們的方法在復(fù)雜的邏輯推理場(chǎng)景下取得了最優(yōu)性能，同時(shí)保持了在簡(jiǎn)單推理場(chǎng)景下的性能。此外，我們觀察到GFaiR產(chǎn)生的推理過(guò)程更加忠實(shí)。

2 背景

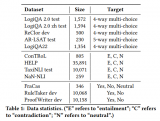
一階邏輯下的自然語(yǔ)言推理: 給定一個(gè)假設(shè)H以及一個(gè)包含一系列事實(shí)和規(guī)則的自然語(yǔ)言理論，目標(biāo)是在不利用外部知識(shí)和常識(shí)知識(shí)的條件下僅僅利用給定的自然語(yǔ)言理論來(lái)判斷假設(shè)H是正確的（True），錯(cuò)誤的（False），還是無(wú)法確定的（Unknown）。每條事實(shí)，規(guī)則和假設(shè)都對(duì)應(yīng)唯一的一階邏輯表示。H的標(biāo)簽是根據(jù)對(duì)事實(shí)和規(guī)則的一階邏輯表示進(jìn)行推理得到的。一個(gè)簡(jiǎn)單的例子如下圖所示：

歸結(jié)反演：在基于邏輯符號(hào)的推理場(chǎng)景下，歸結(jié)反演是一種在一階邏輯下完備的推理方法，也就是說(shuō)，對(duì)于任何一個(gè)在一階邏輯語(yǔ)義下真值為T(mén)rue或者False的假設(shè)，應(yīng)用歸結(jié)反演的推理方法我們都能夠推理出假設(shè)的真值。假設(shè)F為給定前提集對(duì)應(yīng)的一階邏輯公式集合（在基于邏輯符號(hào)的推理場(chǎng)景下每一個(gè)前提都是一個(gè)一階邏輯公式），Q為一個(gè)以一階邏輯公式表示的假設(shè)且在假設(shè)F下Q的真值為T(mén)rue，則證明Q為T(mén)rue的過(guò)程如下所示：

將Q進(jìn)行否定得到?Q，并且將其合并到F中得到{F,?Q}

將{F,?Q}中的每一條進(jìn)行Skolem標(biāo)準(zhǔn)化，從而將其轉(zhuǎn)換為一個(gè)子句集

應(yīng)用歸結(jié)原理對(duì)子句集進(jìn)行歸結(jié)，其中每一步都是根據(jù)子句集中的兩條子句歸結(jié)出一個(gè)新的子句（中間結(jié)論），這個(gè)子句會(huì)被合并到子句集中。這個(gè)歸結(jié)的過(guò)程是迭代式的，直到歸結(jié)出一個(gè)空子句時(shí)停止并說(shuō)明這個(gè)理論集合中存在矛盾，從而進(jìn)一步說(shuō)明Q是正確的。

因此，我們可以首先通過(guò)對(duì)Q和?Q進(jìn)行反演從而得到{F,?Q}以及{F,Q}，然后分別對(duì){F,?Q}以及{F,Q}進(jìn)行歸結(jié)推理并判斷其中是否存在矛盾來(lái)確定Q的真值。如果{F,?Q}不存在矛盾而{F,Q}存在矛盾，則Q為False，反之Q為T(mén)rue，如果都不存在矛盾，則Q為Unknown。

3 方法

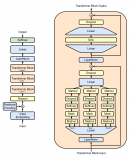
如圖2所示，GFaiR包括5個(gè)模塊：轉(zhuǎn)換器，前選擇器，后選擇器，知識(shí)組裝器，驗(yàn)證器。

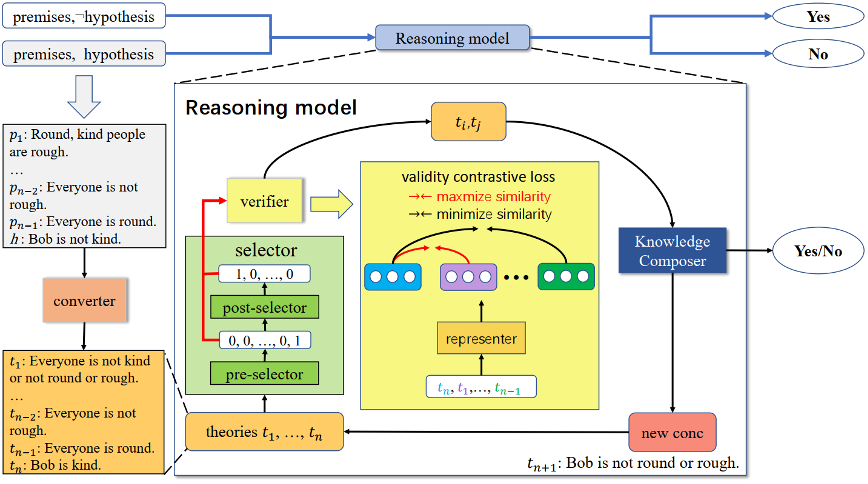
圖2：GFaiR框架圖

3.1 轉(zhuǎn)換器

在執(zhí)行推理之前，基于T5的轉(zhuǎn)換器首先會(huì)將假設(shè)轉(zhuǎn)換為假設(shè)的否定用于后續(xù)進(jìn)行反演推理。接下來(lái)，轉(zhuǎn)換器會(huì)將給定的自然語(yǔ)言理論和假設(shè)（或假設(shè)的否定）轉(zhuǎn)換成Skolem范式形式對(duì)應(yīng)的自然語(yǔ)言表示用于后續(xù)執(zhí)行歸結(jié)推理。為了方便起見(jiàn)，我們將經(jīng)過(guò)轉(zhuǎn)換器轉(zhuǎn)換后的自然語(yǔ)言理論和假設(shè)（或假設(shè)的否定）所組成的整體稱(chēng)為理論集合T，其中的每一條都統(tǒng)一稱(chēng)為理論。

3.2 前選擇器

在每一步推理的過(guò)程中，基于XLNET前選擇器首先根據(jù)理論集合T選擇一條理論用于后續(xù)執(zhí)行歸結(jié)推理。

3.3 后選擇器

在前選擇器選擇了用于歸結(jié)推理的一條理論之后，基于XLNET的后選擇器根據(jù)理論集合T以及前選擇器選擇的理論來(lái)選擇另一條用于后續(xù)執(zhí)行歸結(jié)推理的理論。我們?cè)O(shè)計(jì)這個(gè)模塊是為了顯式地建模前選擇器選擇的理論與其余理論之間的關(guān)系，并利用這一信息來(lái)指導(dǎo)后選擇器的理論選擇過(guò)程。

3.4 知識(shí)組裝器

基于T5的知識(shí)組裝器可以從數(shù)據(jù)中隱式地學(xué)習(xí)歸結(jié)推理規(guī)則，并在自然語(yǔ)言層面對(duì)前選擇器和后選擇器選擇的兩條理論應(yīng)用所學(xué)習(xí)的歸結(jié)推理規(guī)則來(lái)生成新的推論。

3.5 驗(yàn)證器

由于前人的基于transformers的選擇模塊對(duì)于歸結(jié)反演來(lái)說(shuō)不夠準(zhǔn)確，可能會(huì)導(dǎo)致這兩個(gè)選擇器所選擇的理論不相關(guān)，進(jìn)而導(dǎo)致理論上無(wú)法根據(jù)這兩條理論得出一個(gè)符合邏輯的推論（一個(gè)推論是符合邏輯的當(dāng)且僅當(dāng)這個(gè)推論可以根據(jù)這兩條理論推理出來(lái)）。如果知識(shí)組裝器根據(jù)這樣的兩條理論進(jìn)行歸結(jié)推理，那么其生成的推論一定是不合邏輯的，這會(huì)導(dǎo)致歸結(jié)推理的失敗并產(chǎn)生不合邏輯的推論（產(chǎn)生幻覺(jué)）。由于在后續(xù)的推理步驟中我們可能會(huì)用到這個(gè)不合邏輯的推論，因此這可能會(huì)最終導(dǎo)致錯(cuò)誤的推理結(jié)果。為此，我們使用基于合法性對(duì)比損失的驗(yàn)證器來(lái)驗(yàn)證前選擇器和后選擇器選擇的兩個(gè)理論，以確保在理論上可以通過(guò)對(duì)這兩條理論執(zhí)行邏輯推理來(lái)得出符合邏輯的推論，從而為歸結(jié)推理提供了保證，并通過(guò)減少幻覺(jué)來(lái)提高模型的忠實(shí)性。

3.6 推理過(guò)程

在推理時(shí)，轉(zhuǎn)換器首先將給定的自然語(yǔ)言理論和假設(shè)（或假設(shè)的否定）轉(zhuǎn)換成兩個(gè)理論集合，其中每條理論的表示都是Skolem范式形式對(duì)應(yīng)的自然語(yǔ)言表示。其中一個(gè)理論集合包括自然語(yǔ)言理論和假設(shè)，另一個(gè)包括自然語(yǔ)言理論和假設(shè)的否定。接下來(lái)我們對(duì)這兩個(gè)理論集合應(yīng)用圖2中的推理模型（Reasoning model）來(lái)推斷其是否存在矛盾，從而判斷假設(shè)的真值。

對(duì)于一個(gè)具體的理論集合T，前選擇器首先選擇一條理論，接下來(lái)，在驗(yàn)證器的指導(dǎo)下，后選擇器選擇一個(gè)能夠與組成一個(gè)合法理論對(duì)的理論，如果不存在這樣的理論，則停止并認(rèn)為T(mén)中不存在矛盾，否則，知識(shí)組裝器會(huì)對(duì)這兩條理論進(jìn)行自然語(yǔ)言層面的歸結(jié)推理并得出一個(gè)新的推論，如果這個(gè)推論是一個(gè)空字符串（對(duì)應(yīng)空子句），則停止并認(rèn)為這個(gè)理論集合存在矛盾。反之，新生成的推論會(huì)被合并到T中參與接下來(lái)的推理過(guò)程。

4 實(shí)驗(yàn)

4.1 數(shù)據(jù)集&評(píng)測(cè)指標(biāo)

為了驗(yàn)證GFaiR，我們采用RuleTaker-3ext-sat數(shù)據(jù)集進(jìn)行訓(xùn)練，然后在RuleTaker-3ext-sat，Ruletaker-depth-5，以及更加復(fù)雜的Hard RuleTaker數(shù)據(jù)集上進(jìn)行測(cè)試。此外，由于Hard RuleTaker數(shù)據(jù)集中沒(méi)有標(biāo)簽為Unknown的數(shù)據(jù)，我們遵循前人的方法來(lái)采樣標(biāo)簽為Unknown的數(shù)據(jù)并將其添加到Hard RuleTaker數(shù)據(jù)集中以構(gòu)造一個(gè)標(biāo)簽平衡的數(shù)據(jù)集，并將這個(gè)新的數(shù)據(jù)集稱(chēng)為Hard RuleTaker*。此外，為了比較我們的方法在復(fù)雜的邏輯推理場(chǎng)景下的in-domain性能，我們將Hard RuleTaker*數(shù)據(jù)集按照8.5,0.5,1的比例將其拆分為訓(xùn)練集，驗(yàn)證集，測(cè)試集。拆分后的數(shù)據(jù)集我們將其命名為Hard RuleTaker**。

我們的評(píng)價(jià)指標(biāo)包括兩個(gè)方面：（1）Entailment accuracy (EA)：衡量模型預(yù)測(cè)假設(shè)標(biāo)簽的準(zhǔn)確率。（2）Full accuracy (FA): 衡量模型預(yù)測(cè)假設(shè)標(biāo)簽和推理過(guò)程同時(shí)正確的準(zhǔn)確率

4.2 主實(shí)驗(yàn)

我們將GFaiR與基于預(yù)訓(xùn)練模型的方法以及基于分步推理的方法IBR, FaiRR, NLProofs進(jìn)行對(duì)比，主實(shí)驗(yàn)結(jié)果如表1所示：可以看出，我們的方法在簡(jiǎn)單的推理場(chǎng)景下保持了性能，同時(shí)在復(fù)雜的推理場(chǎng)景下性能遠(yuǎn)遠(yuǎn)超過(guò)基于預(yù)訓(xùn)練模型的方法以及基于分步推理的方法，這說(shuō)明通過(guò)結(jié)合歸結(jié)反演，GFaiR的完備性得到了改善，在復(fù)雜推理情境下的zero-shot泛化能力更強(qiáng)。根據(jù)EA和FA的差值，我們也可以看出GFaiR產(chǎn)生的推理過(guò)程是忠實(shí)的。雖然NLProofs和FaiRR在Hard RT和Hard RT*數(shù)據(jù)集上EA和FA之間的差值更小，但是它們的EA較低，在這種情況下單純考慮其忠實(shí)性是沒(méi)有意義的。

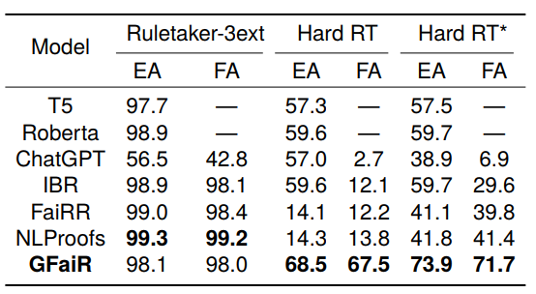
表1：主實(shí)驗(yàn)結(jié)果

4.3 推理深度泛化實(shí)驗(yàn)

我們通過(guò)將不同模型在推理深度小于等于3的RuleTaker-3ext-sat數(shù)據(jù)集進(jìn)行訓(xùn)練，然后在推理深度小于等于5的Ruletaker-depth-5數(shù)據(jù)集上進(jìn)行測(cè)試來(lái)評(píng)估不同方法在推理深度上的泛化能力，結(jié)果如表2所示：可以看出，當(dāng)推理深度增加時(shí)，GFaiR的性能下降更小，比如當(dāng)推理深度從3增加到5時(shí)，GFaiR的EA值下降了1.6%，而FaiRR和NLProofs則分別下降了14.4%和24.5%，這說(shuō)明GFaiR對(duì)于推理深度的泛化能力更強(qiáng)。

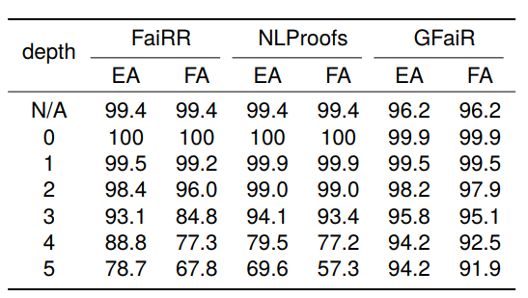
表2：推理深度泛化實(shí)驗(yàn)

4.4 復(fù)雜推理場(chǎng)景下的in-domain實(shí)驗(yàn)

我們通過(guò)將不同模型在Hard RuleTaker**數(shù)據(jù)集上進(jìn)行訓(xùn)練和測(cè)試來(lái)評(píng)價(jià)不同方法在復(fù)雜推理情景下的in-domain性能，實(shí)驗(yàn)結(jié)果如表3所示：可以看出，GFaiR在Hard RuleTaker**數(shù)據(jù)集上實(shí)現(xiàn)了最佳性能，這說(shuō)明通過(guò)引入歸結(jié)反演，GFaiR方法在復(fù)雜推理情景下更加有效。

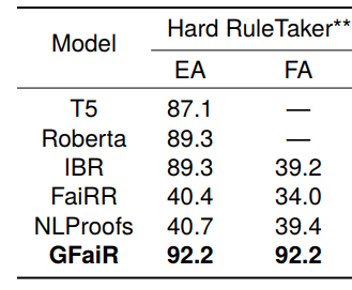
表3：復(fù)雜推理場(chǎng)景下的in-domain性能

5 總結(jié)

在本文中，通過(guò)引入歸結(jié)反演和基于合法性對(duì)比損失的驗(yàn)證器，我們提出了一個(gè)泛化能力強(qiáng)且忠實(shí)的推理方法GFaiR，該方法能夠處理復(fù)雜的邏輯推理場(chǎng)景。實(shí)驗(yàn)結(jié)果還表明，在較為復(fù)雜的Hard RuleTaker和Hard RuleTaker*數(shù)據(jù)集上，GFaiR能夠?qū)崿F(xiàn)更好的性能。

審核編輯：黃飛

?