在本文中會(huì)站在代碼的角度上為你解讀深度學(xué)習(xí)的前世今生，文章根據(jù)六段代碼從不同的階段解說(shuō)，并將相關(guān)的代碼示例都上傳展示了。如果你是FloydHub新手，在本地計(jì)算機(jī)上的示例項(xiàng)目文件夾中安裝好CLI之后，可以使用以下命令在FloydHub上啟動(dòng)項(xiàng)目：

　　接下來(lái)我們一起跟著原作者細(xì)讀這六段極富歷史意義歷史的代碼，最小二乘法

　　最小二乘法最初是由法國(guó)數(shù)學(xué)家勒讓德（Adrien-Marie Legendre）提出的，他曾因參與標(biāo)準(zhǔn)米的制定而聞名。勒讓德癡迷于預(yù)測(cè)彗星的位置，基于彗星曾出現(xiàn)過(guò)的幾處位置，百折不撓的計(jì)算彗星的軌道，在經(jīng)歷無(wú)數(shù)的測(cè)試后，他終于想出了一種方法平衡計(jì)算誤差，隨后在其1805年的著作《計(jì)算慧星軌道的新方法》中發(fā)表了這一思想，也就是著名的最小二乘法。

　　勒讓德將最小二乘法運(yùn)用于計(jì)算彗星軌道，首先是猜測(cè)彗星將來(lái)出現(xiàn)的位置，然后計(jì)算這一猜測(cè)值的平方誤差，最后通過(guò)修正猜測(cè)值來(lái)減少平方誤差的總和，這就是線性回歸思想的源頭。

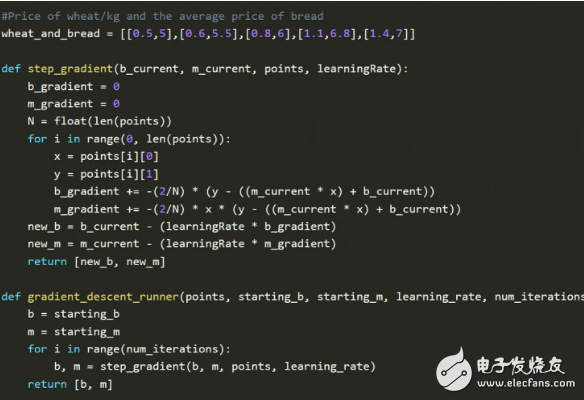
　　在Jupyter notebook上執(zhí)行上圖的代碼。 m是系數(shù)，b是預(yù)測(cè)常數(shù)，XY坐標(biāo)表示彗星的位置，因此函數(shù)的目標(biāo)是找到某一特定m和b的組合，使得誤差盡可能地小。

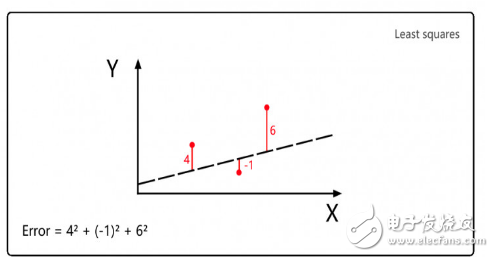
　　這也是深度學(xué)習(xí)的核心思想：給定輸入和期望輸出，尋找兩者之間的關(guān)聯(lián)性。

　　梯度下降

　　勒讓德的方法是在誤差函數(shù)中尋找特定組合的m和b，確定誤差的最小值，但這一方法需要人工調(diào)節(jié)參數(shù)，這種手動(dòng)調(diào)參來(lái)降低錯(cuò)誤率的方法是非常耗時(shí)的。在一個(gè)世紀(jì)后，荷蘭諾貝爾獎(jiǎng)得主彼得·德比（Peter Debye）對(duì)勒讓德的方法進(jìn)行了改良。

　　假設(shè)勒讓德需要修正一個(gè)參數(shù)X，Y軸表示不同X值的誤差。勒讓德希望找到這樣一個(gè)X，使得誤差Y最小。如下圖，我們可以看出，當(dāng)X=1.1時(shí)，誤差Y的值最小。

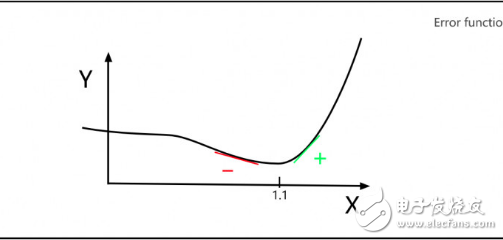
　　如上圖，德比注意到，最小值左邊的斜率都是負(fù)數(shù)，最小值右邊的斜率都是正數(shù)。因此，如果你知道任意點(diǎn)X值所處的斜率，就能判斷最小的Y值在這一點(diǎn)的左邊還是右邊，所以接下來(lái)你會(huì)盡可能往接近最小值的方向去選擇X值。

　　這就引入了梯度下降的概念，幾乎所有深度學(xué)習(xí)的模型都會(huì)運(yùn)用到梯度下降。

　　假設(shè)誤差函數(shù) Error = X5 - 2X3 - 2

　　求導(dǎo)來(lái)計(jì)算斜率：

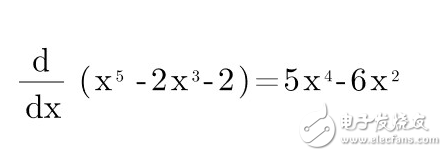
　　如果讀者需要補(bǔ)充導(dǎo)數(shù)的知識(shí)，可以學(xué)習(xí)Khan Academy的視頻。

　　下圖的python代碼解釋了德比的數(shù)學(xué)方法：

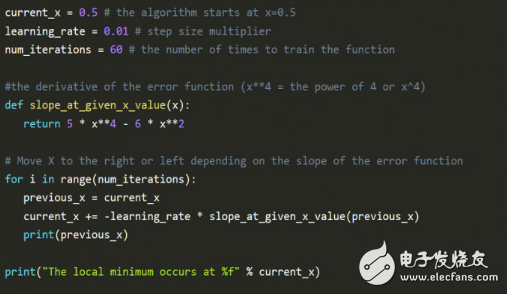
　　上圖代碼最值得注意的是學(xué)習(xí)率 learning_rate，通過(guò)向斜率的反方向前進(jìn)，慢慢接近最小值。當(dāng)越接近最小值時(shí)，斜率會(huì)變得越來(lái)越小，慢慢逼近于0，這就是最小值處。

　　Num_iterations 表示在找到最小值前估算的迭代次數(shù)。

　　運(yùn)行上述代碼，讀者可以自行調(diào)參來(lái)熟悉梯度下降。

　　線性回歸

　　線性回歸算法結(jié)合了最小二乘法和梯度下降。在二十世紀(jì)五六十年代，一組經(jīng)濟(jì)學(xué)家在早期計(jì)算機(jī)上實(shí)現(xiàn)了線性回歸的早期思想。他們使用穿孔紙帶來(lái)編程，這是非常早期的計(jì)算機(jī)編程方法，通過(guò)在紙帶上打上一系列有規(guī)律的孔點(diǎn)，光電掃描輸入電腦。經(jīng)濟(jì)學(xué)家們花了好幾天來(lái)打孔，在早期計(jì)算機(jī)上運(yùn)行一次線性回歸需要24小時(shí)以上。

　　下圖是Python實(shí)現(xiàn)的線性回歸。

　　梯度下降和線性回歸都不是什么新算法，但是兩者的結(jié)合效果還是令人驚嘆，可以試試這個(gè)線性回歸模擬器來(lái)熟悉下線性回歸。

　　感知機(jī)

　　感知機(jī)最早由康奈爾航空實(shí)驗(yàn)室的心理學(xué)家弗蘭克·羅森布拉特（Frank Rosenblatt）提出，羅森布拉特除了研究大腦學(xué)習(xí)能力，還愛(ài)好天文學(xué)，他能白天解剖蝙蝠研究學(xué)習(xí)遷移能力，夜晚還跑到自家屋后山頂建起天文臺(tái)研究外太空生命。1958年，羅森布拉特模擬神經(jīng)元發(fā)明感知機(jī)，以一篇《New Navy Device Learns By Doing》登上紐約時(shí)報(bào)頭條。

　　羅森布拉特這臺(tái)機(jī)器很快吸引了大眾視線，給這臺(tái)機(jī)器看50組圖片（每組由一張標(biāo)識(shí)向左和一張標(biāo)識(shí)向右的圖片組成），在沒(méi)有預(yù)先設(shè)定編程命令的情況下，機(jī)器可以識(shí)別出圖片的標(biāo)識(shí)方向。

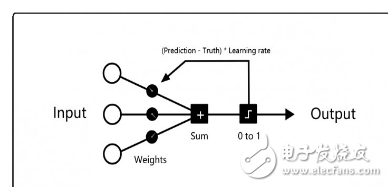
　　每一次的訓(xùn)練過(guò)程都是以左邊的輸入神經(jīng)元開(kāi)始，給每個(gè)輸入神經(jīng)元都賦上隨機(jī)權(quán)重，然后計(jì)算所有加權(quán)輸入的總和，如果總和是負(fù)數(shù)，則標(biāo)記預(yù)測(cè)結(jié)果為0，否則標(biāo)記預(yù)測(cè)結(jié)果為1。

　　如果預(yù)測(cè)是正確的，不需要修改權(quán)重；如果預(yù)測(cè)是錯(cuò)誤的，用學(xué)習(xí)率（learning_rate）乘以誤差來(lái)對(duì)應(yīng)地調(diào)整權(quán)重。

　　下面我們來(lái)看看感知機(jī)如何解決傳統(tǒng)的或邏輯（OR）。

　　Python實(shí)現(xiàn)感知機(jī)：

　　等人們對(duì)感知機(jī)的興奮勁頭過(guò)后，馬文·明斯基（Marvin Minsky）和西摩·帕普特（Seymour Papert） 打破了人們對(duì)這一思想的崇拜。當(dāng)時(shí)明斯基和帕普特都在MIT的AI實(shí)驗(yàn)室工作，他們寫(xiě)了一本書(shū)證明感知機(jī)只能解決線性問(wèn)題，指出了感知機(jī)無(wú)法解決異或問(wèn)題（XOR）的缺陷。很遺憾，羅森布拉特在兩年后的一場(chǎng)船難中遇難離世。

　　在明斯基和帕普特提出這一點(diǎn)的一年后，一位芬蘭的碩士學(xué)生找到了解決非線性問(wèn)題的多層感知機(jī)算法。當(dāng)時(shí)因?yàn)閷?duì)感知機(jī)的批判思想占主流，AI領(lǐng)域的投資已經(jīng)干枯幾十年了，這就是著名的第一次AI寒冬。

　　明斯基和帕普特批判感知機(jī)無(wú)法解決異或問(wèn)題（XOR，要求1&1返回0）：

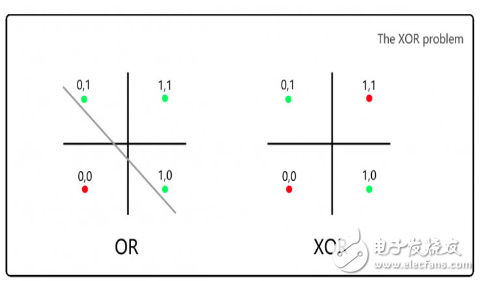
　　對(duì)于左圖的OR邏輯，我們可以通過(guò)一條線分開(kāi)0和1的情形，但是對(duì)于右邊的XOR邏輯，無(wú)法用一條線來(lái)劃分。

　　人工神經(jīng)網(wǎng)絡(luò)

　　到了1986年，魯梅爾哈特（David Everett Rumelhart）、杰弗里·辛頓（Geoffrey Hinton）等人提出反向傳播算法，證明了神經(jīng)網(wǎng)絡(luò)是可以解決復(fù)雜的非線性問(wèn)題的。當(dāng)這種理論提出來(lái)時(shí)，計(jì)算機(jī)相比之前已經(jīng)快了1000倍。讓我們看看魯梅爾哈特等人如何介紹這篇具有重大里程碑意義的論文：

　　我們?yōu)樯窠?jīng)元網(wǎng)絡(luò)提出了一種新的學(xué)習(xí)過(guò)程——反向傳播。 反向傳播不斷地調(diào)整網(wǎng)絡(luò)中的連接權(quán)重，最小化實(shí)際輸出與期望輸出之間的誤差。 由于權(quán)重調(diào)整，我們加入了隱藏神經(jīng)元，這些神經(jīng)元既不屬于輸入層，也不屬于輸出層，他們提取了任務(wù)的重要特征，并對(duì)輸出進(jìn)行了正則化。反向傳播這種創(chuàng)造有效特征的能力，將其與之前的算法（如感知器收斂過(guò)程）區(qū)別開(kāi)來(lái)。

　　Nature 323，533-536（1986年10月9日）

　　為了理解這篇論文的核心，我們實(shí)現(xiàn)了DeepMind大神Andrew Trask的代碼，這并不是隨機(jī)選擇的代碼，這段代碼被Andrew Karpathy斯坦福的深度學(xué)習(xí)課程、Siraj Raval在Udacity的課程中采用。更為重要的是，這段代碼體現(xiàn)的思想解決了XOR問(wèn)題，融化了AI的第一個(gè)冬季。

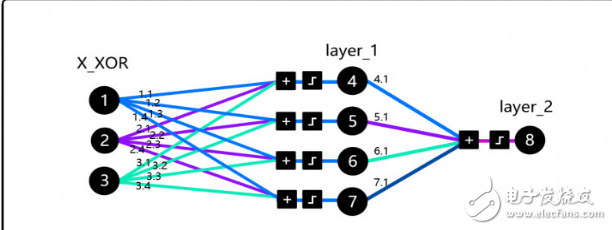
　　在我們繼續(xù)深入之前，讀者可以試試這個(gè)模擬器，花上一兩個(gè)小時(shí)來(lái)熟悉核心概念，然后再讀Trask的博客，接下來(lái)多熟悉代碼。注意在X_XOR數(shù)據(jù)中增加的參數(shù)是偏置神經(jīng)元（bias neurons），類(lèi)似于線性函數(shù)中的常量。

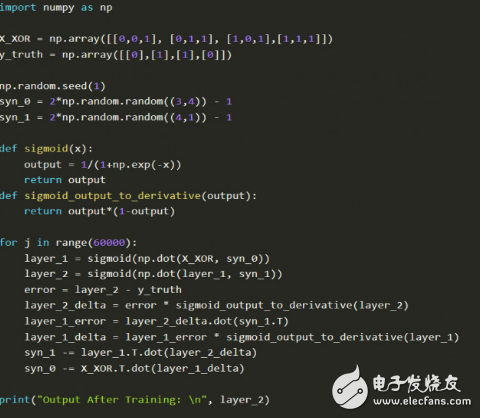
　　這里結(jié)合的反向傳播，矩陣乘法和梯度下降可能會(huì)繞暈?zāi)悖x者可以通過(guò)可視化過(guò)程來(lái)理解。先注重去看背后的邏輯，不要想著一下子就能完全參透全部。

　　另外，讀者可以看看Andrew Karpathy的反向傳播那一課，玩轉(zhuǎn)一下可視化過(guò)程，讀讀邁克爾·尼爾森（Michael Nielsen）的《神經(jīng)網(wǎng)絡(luò)與深度學(xué)習(xí)》書(shū)上這一章。

　　深度神經(jīng)網(wǎng)絡(luò)

　　深度神經(jīng)網(wǎng)絡(luò)指的是除了輸入層和輸出層，中間還存在多層網(wǎng)絡(luò)的神經(jīng)網(wǎng)絡(luò)模型，這一概念首先由加利福尼亞大學(xué)計(jì)算機(jī)系認(rèn)知系統(tǒng)實(shí)驗(yàn)室的Rina Dechter提出，可參考其論文《Learning While Searching in Constraint-Satisfaction-Problems》，但深度神經(jīng)網(wǎng)絡(luò)的概念在2012年才得到主流的關(guān)注，不久后IBM IBM Watson在美國(guó)智力游戲危險(xiǎn)邊緣（eopardy）取得勝利，谷歌推出了貓臉識(shí)別。

　　深層神經(jīng)網(wǎng)絡(luò)的核心結(jié)構(gòu)仍保持不變，但現(xiàn)在開(kāi)始被應(yīng)用在不同的問(wèn)題上， 正規(guī)化也有很大的提升。一組最初應(yīng)用于簡(jiǎn)化噪音數(shù)據(jù)的數(shù)學(xué)函數(shù)，現(xiàn)在被用于神經(jīng)網(wǎng)絡(luò)，提高神經(jīng)網(wǎng)絡(luò)的泛化能力。

　　深度學(xué)習(xí)的創(chuàng)新很大一部分要?dú)w功于計(jì)算能力的飛速提升，這一點(diǎn)改進(jìn)了研究者的創(chuàng)新周期，那些原本需要一個(gè)八十年代中期的超級(jí)計(jì)算機(jī)計(jì)算一年的任務(wù)，今天用GPU只需要半秒鐘就可以完成。

　　計(jì)算方面的成本降低以及深度學(xué)習(xí)越來(lái)越豐富的庫(kù)資源，使得大眾也可以走進(jìn)這一行。我們來(lái)看一個(gè)普通的深層學(xué)習(xí)堆棧的例子，從底層開(kāi)始：

　　GPU 》 Nvidia Tesla K80。通常用于圖像處理，對(duì)比CPU，他們?cè)谏疃葘W(xué)習(xí)任務(wù)的速度快了50-200倍。

　　CUDA 》 GPU的底層編程語(yǔ)言。

　　CuDNN 》 Nvidia優(yōu)化CUDA的庫(kù)

　　Tensorflow 》 Google的深度學(xué)習(xí)框架

　　TFlearn 》 Tensorflow的前端框架

　　我們來(lái)看一個(gè)數(shù)字分類(lèi)的例子（MNIST數(shù)據(jù)集），這是一個(gè)入門(mén)級(jí)的例子，深度學(xué)習(xí)界的“hello world”。

　　在TFlearn中實(shí)現(xiàn)：

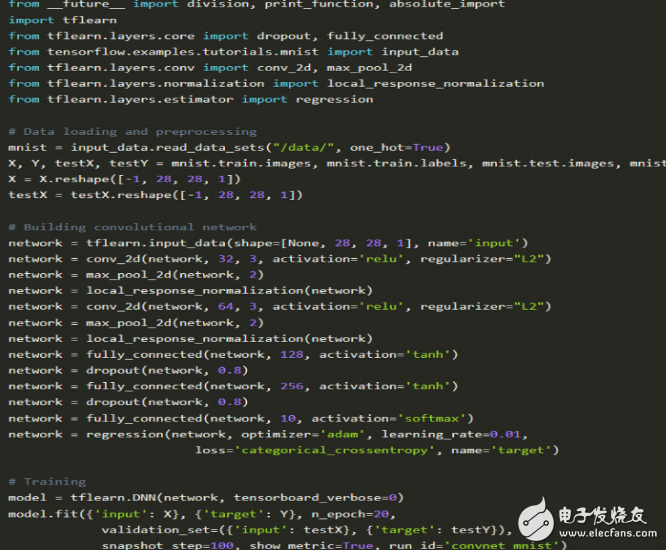
　　有很多經(jīng)典的文章解釋了MNIST問(wèn)題，參考Tensorflow文檔、Justin Francis的文章以及Sentdex發(fā)布的視頻。

　　如果讀者還想對(duì)TFlearn有進(jìn)一步了解，可參考作者Emil Wallner之前的博客文章。

　　總結(jié)

　　如同上圖的TFlearn示例，深度學(xué)習(xí)的主要思想仍然很像多年前羅森布拉特提出的感知機(jī)，但已經(jīng)不再使用二進(jìn)制赫維賽德階躍函數(shù)（Heaviside step function），今天的神經(jīng)網(wǎng)絡(luò)大多使用Relu激活函數(shù)。在卷積神經(jīng)網(wǎng)絡(luò)的最后一層，損失設(shè)置為多分類(lèi)的對(duì)數(shù)損失函數(shù)categorical_crossentropy，這是對(duì)勒讓德最小二乘法的一大改良，使用邏輯回歸來(lái)解決多類(lèi)別問(wèn)題。另外優(yōu)化算法Adam則起源于德比的梯度下降思想。此外， Tikhonov的正則化思想被廣泛地應(yīng)用于Dropout層和L1 / L2層的正則化函數(shù)。