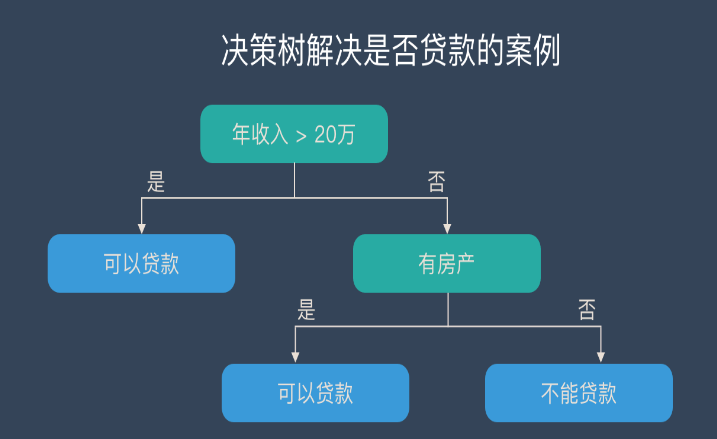
決策樹,是機器學習中一種非常常見的分類方法,也可以說是所有算法中最直觀也最好理解的算法。
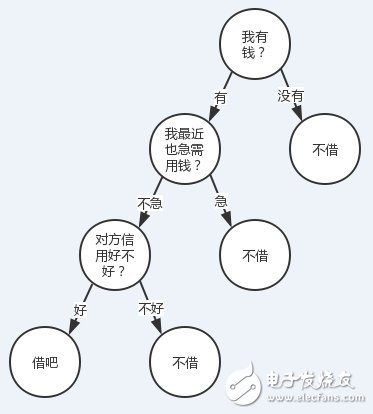
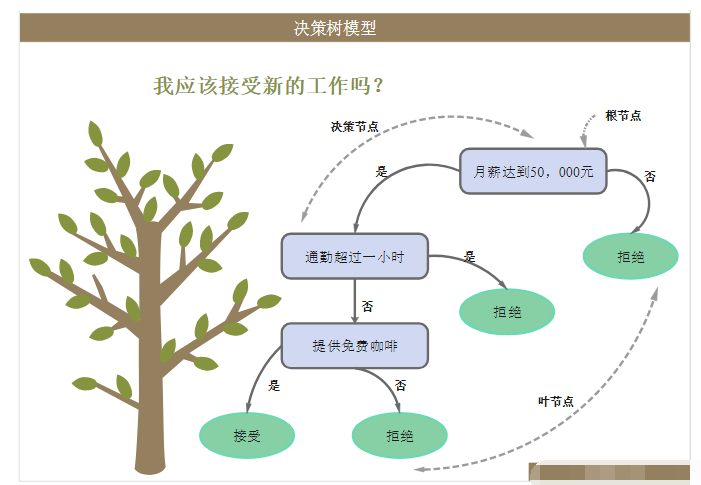
有人找我借錢(當然不太可能。。。),借還是不借?我會結合根據我自己有沒有錢、我自己用不用錢、對方信用好不好這三個特征來決定我的答案。
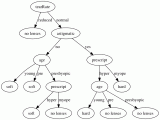
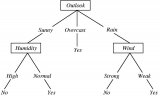
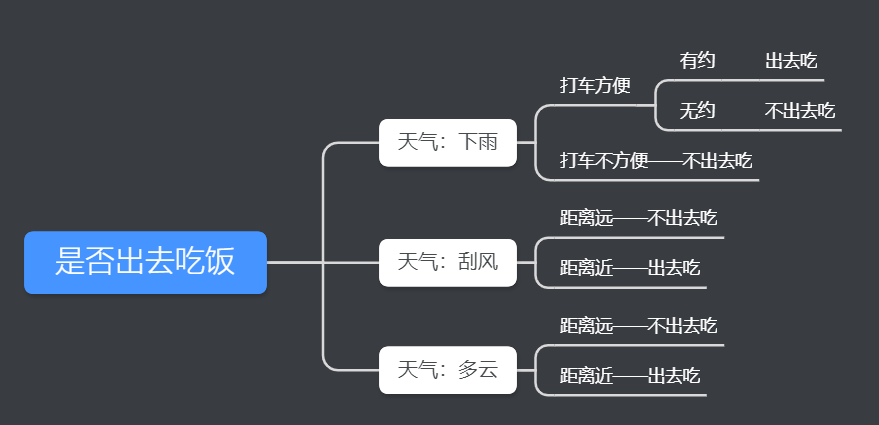
我們把轉到更普遍一點的視角,對于一些有特征的數據,如果我們能夠有這么一顆決策樹,我們也就能非常容易地預測樣本的結論。所以問題就轉換成怎么求一顆合適的決策樹,也就是怎么對這些特征進行排序。
在對特征排序前先設想一下,對某一個特征進行決策時,我們肯定希望分類后樣本的純度越高越好,也就是說分支結點的樣本盡可能屬于同一類別。
所以在選擇根節點的時候,我們應該選擇能夠使得“分支結點純度最高”的那個特征。在處理完根節點后,對于其分支節點,繼續套用根節點的思想不斷遞歸,這樣就能形成一顆樹。這其實也是貪心算法的基本思想。那怎么量化“純度最高”呢?熵就當仁不讓了,它是我們最常用的度量純度的指標。其數學表達式如下:
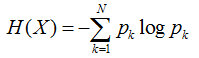
其中N表示結論有多少種可能取值,p表示在取第k個值的時候發生的概率,對于樣本而言就是發生的頻率/總個數。
熵越小,說明樣本越純。
以一個兩點分布樣本X(x=0或1)的熵的函數圖像來說明吧,橫坐標表示樣本值為1的概率,縱坐標表示熵。
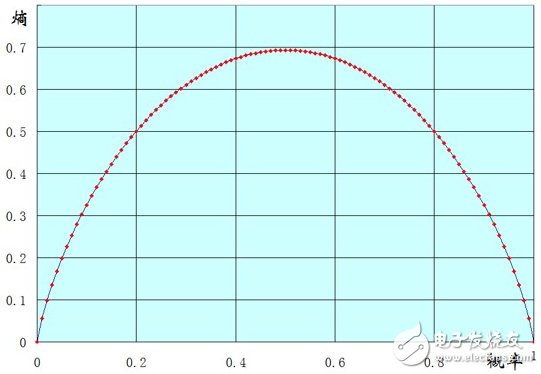
可以看到到當p(x=1)=0時,也就是說所有的樣本都為0,此時熵為0.
當p(x=1)=1時,也就是說所有的樣本都為1,熵也為0.
當p(x=1)=0.5時,也就是樣本中0,1各占一半,此時熵能取得最大值。
擴展一下,樣本X可能取值為n種(x1。。。。xn)。可以證明,當p(xi)都等于1/n 時,也就是樣本絕對均勻,熵能達到最大。當p(xi)有一個為1,其他都為0時,也就是樣本取值都是xi,熵最小。
決策樹算法
ID3
假設在樣本集X中,對于一個特征a,它可能有(a1,a2。。。an)這些取值,如果用特征a對樣本集X進行劃分(把它當根節點),肯定會有n個分支結點。剛才提了,我們希望劃分后,分支結點的樣本越純越好,也就是分支結點的“總熵”越小越好。
因為每個分支結點的個數不一樣,因此我們計算“總熵”時應該做一個加權,假設第i個結點樣本個數為W(ai),其在所有樣本中的權值為W(ai) / W(X)。所以我們可以得到一個總熵:
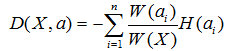
這個公式代表含義一句話:加權后各個結點的熵的總和。這個值應該越小,純度越高。
這時候,我們引入一個名詞叫信息增益G(X,a),意思就是a這個特征給樣本帶來的信息的提升。公式就是:![]() ,由于H(X)對一個樣本而言,是一個固定值,因此信息增益G應該越大越好。尋找使得信息增益最大的特征作為目標結點,并逐步遞歸構建樹,這就是ID3算法的思想,好了以一個簡單的例子來說明信息增益的計算:
,由于H(X)對一個樣本而言,是一個固定值,因此信息增益G應該越大越好。尋找使得信息增益最大的特征作為目標結點,并逐步遞歸構建樹,這就是ID3算法的思想,好了以一個簡單的例子來說明信息增益的計算:

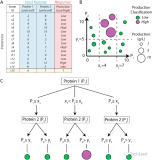
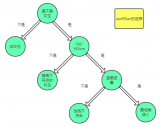
上面的例子,我計算一下特征1的信息增益
首先計算樣本的熵H(X)
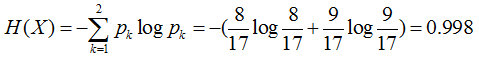
再計算總熵,可以看到特征1有3個結點A、B、C,其分別為6個、6個、5個
所以A的權值為6/(6+6+5), B的權值為6/(6+6+5), C的為5/(6+6+5)
因為我們希望劃分后結點的純度越高越好,因此還需要再分別計算結點A、B、C的熵
特征1=A:3個是、3個否,其熵為

特征1=B:2個是、4個否,其熵為
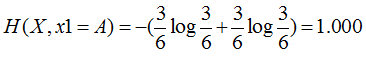
特征1=C:4個是、1個否,其熵為
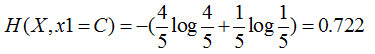
這樣分支結點的總熵就等于:

特征1的信息增益就等于0.998-0.889=0.109
類似地,我們也能算出其他的特征的信息增益,最終取信息增益最大的特征作為根節點。
以上計算也可以有經驗條件熵來推導:G(X,A)=H(X) - H(X|A),這部分有興趣的同學可以了解一下。
C4.5
在ID3算法中其實有個很明顯的問題。
如果有一個樣本集,它有一個叫id或者姓名之類的(唯一的)的特征,那就完蛋了。設想一下,如果有n個樣本,id這個特征肯定會把這個樣本也分成n份,也就是有n個結點,每個結點只有一個值,那每個結點的熵就為0。就是說所有分支結點的總熵為0,那么這個特征的信息增益一定會達到最大值。因此如果此時用ID3作為決策樹算法,根節點必然是id這個特征。但是顯然這是不合理的。。。
當然上面說的是極限情況,一般情況下,如果一個特征對樣本劃分的過于稀疏,這個也是不合理的(換句話就是,偏向更多取值的特征)。為了解決這個問題,C4.5算法采用了信息增益率來作為特征選取標準。
所謂信息增益率,是在信息增益基礎上,除了一項split information,來懲罰值更多的屬性。
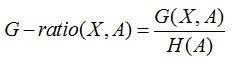
而這個split information其實就是特征個數的熵H(A)。
為什么這樣可以減少呢,以上面id的例子來理解一下。如果id把n個樣本分成了n份,那id這個特征的取值的概率都是1/n,文章引言已經說了,樣本絕對均勻的時候,熵最大。
因此這種情況,以id為特征,雖然信息增益最大,但是懲罰因子split information也最大,以此來拉低其增益率,這就是C4.5的思想。
CART
決策樹的目的最終還是尋找到區分樣本的純度的量化標準。在CART決策樹中,采用的是基尼指數來作為其衡量標準。基尼系數直觀的理解是,從集合中隨機抽取兩個樣本,如果樣本集合越純,取到不同樣本的概率越小。這個概率反應的就是基尼系數。
因此如果一個樣本有K個分類。假設樣本的某一個特征a有n個取值的話,其某一個結點取到不同樣本的概率為:![]()
因此k個分類的概率總和,我們稱之為基尼系數:
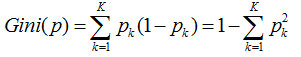
而基尼指數,則是對所有結點的基尼系數進行加權處理
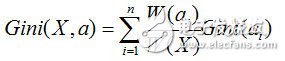
計算出來后,我們會選擇基尼系數最小的那個特征作為最優劃分特征。
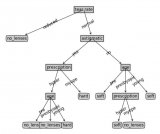
剪枝
剪枝的目的其實就是防止過擬合,它是決策樹防止過擬合的最主要手段。決策樹中,為了盡可能爭取的分類訓練樣本,所以我們的決策樹也會一直生長。但是呢,有時候訓練樣本可能會學的太好,以至于把某些樣本的特有屬性當成一般屬性。這時候就我們就需要主動去除一些分支,來降低過擬合的風險。
剪枝一般有兩種方式:預剪枝和后剪枝。
預剪枝
一般情況下,只要結點樣本已經100%純了,樹才會停止生長。但這個可能會產生過擬合,因此我們沒有必要讓它100%生長,所以在這之前,設定一些終止條件來提前終止它。這就叫預剪枝,這個過程發生在決策樹生成之前。
一般我們預剪枝的手段有:
1、限定樹的深度
2、節點的子節點數目小于閾值
3、設定結點熵的閾值等等。
后剪枝
顧名思義,這個剪枝是在決策樹建立過程后。后剪枝算法的算法很多,有些也挺深奧,這里提一個簡單的算法的思想,就不深究啦。
Reduced-Error Pruning (REP)
該剪枝方法考慮將樹上的每個節點都作為修剪的候選對象,但是有一些條件決定是否修剪,通常有這幾步:
1、刪除其所有的子樹,使其成為葉節點。
2、賦予該節點最關聯的分類
3、用驗證數據驗證其準確度與處理前比較
如果不比原來差,則真正刪除其子樹。然后反復從下往上對結點處理。這個處理方式其實是處理掉那些“有害”的節點。
隨機森林
隨機森林的理論其實和決策樹本身不應該牽扯在一起,決策樹只能作為其思想的一種算法。
為什么要引入隨機森林呢。我們知道,同一批數據,我們只能產生一顆決策樹,這個變化就比較單一了。還有要用多個算法的結合呢?
這就有了集成學習的概念。
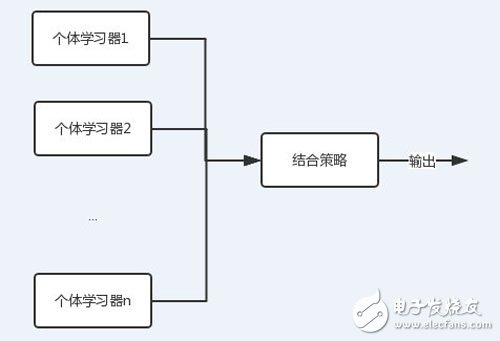
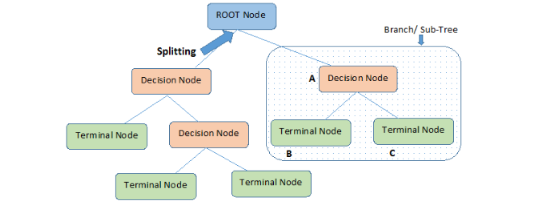
圖中可以看到,每個個體學習器(弱學習器)都可包含一種算法,算法可以相同也可以不同。如果相同,我們把它叫做同質集成,反之則為異質。
隨機森林則是集成學習采用基于bagging策略的一個特例。
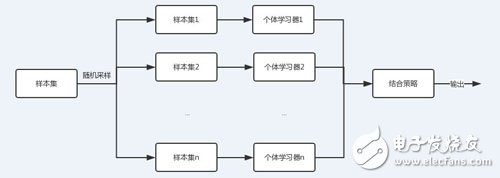
從上圖可以看出,bagging的個體學習器的訓練集是通過隨機采樣得到的。通過n次的隨機采樣,我們就可以得到n個樣本集。對于這n個樣本集,我們可以分別獨立的訓練出n個個體學習器,再對這n個個體學習器通過集合策略來得到最終的輸出,這n個個體學習器之間是相互獨立的,可以并行。
注:集成學習還有另一種方式叫boosting,這種方式學習器之間存在強關聯,有興趣的可以了解下。
隨機森林采用的采樣方法一般是是Bootstap sampling,對于原始樣本集,我們每次先隨機采集一個樣本放入采樣集,然后放回,也就是說下次采樣時該樣本仍有可能被采集到,經過一定數量的采樣后得到一個樣本集。由于是隨機采樣,這樣每次的采樣集是和原始樣本集不同的,和其他采樣集也是不同的,這樣得到的個體學習器也是不同的。
隨機森林最主要的問題是有了n個結果,怎么設定結合策略,主要方式也有這么幾種:
加權平均法:
平均法常用于回歸。做法就是,先對每個學習器都有一個事先設定的權值wi,
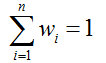
然后最終的輸出就是:
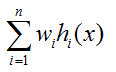
當學習器的權值都為1/n時,這個平均法叫簡單平均法。
投票法:
投票法類似我們生活中的投票,如果每個學習器的權值都是一樣的。
那么有絕對投票法,也就是票數過半。相對投票法,少數服從多數。
如果有加權,依然是少數服從多數,只不過這里面的數是加權后的。
例子
以一個簡單的二次函數的代碼來看看決策樹怎么用吧。
訓練數據是100個隨機的真實的平方數據,不同的深度將會得到不同的曲線
測試數據也是隨機數據,但是不同深度的樹的模型,產生的預測值也不太一樣。如圖
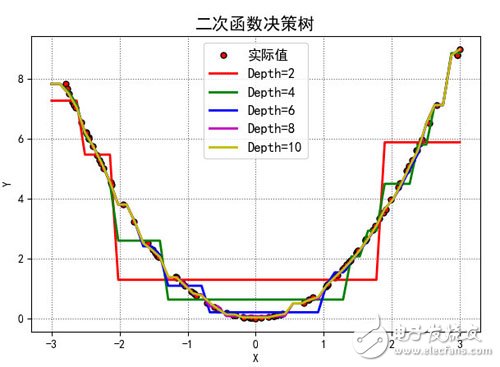
這幅圖的代碼如下:


我的是python 3.6環境,需要安裝numpy、matplotlib、sklearn這三個庫,需要的話直接pip install,大家可以跑跑看看,雖然簡單但挺有趣。
 電子發燒友App
電子發燒友App










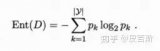




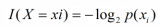











評論