本書節(jié)選自圖書,Python本身帶有許多機器學(xué)習(xí)的第三方庫,但本書在絕大多數(shù)情況下只會用到Numpy這個基礎(chǔ)的科學(xué)計算庫來進行算法代碼的實現(xiàn)。這樣做的目的是希望讀者能夠從實現(xiàn)的過程中更好地理解機器學(xué)習(xí)算法的細節(jié),以及了解Numpy的各種應(yīng)用。不過作為補充,本書會在適當(dāng)?shù)臅r候應(yīng)用scikit-learn這個成熟的第三方庫中的模型。
“機器學(xué)習(xí)”在最近雖可能不至于到人盡皆知的程度,卻也是非常火熱的詞匯。機器學(xué)習(xí)是英文單詞“Machine Learning”(簡稱ML)的直譯,從字面上便說明了這門技術(shù)是讓機器進行“學(xué)習(xí)”的技術(shù)。然而我們知道機器終究是死的,所謂的“學(xué)習(xí)”歸根結(jié)底亦只是人類“賦予”機器的一系列運算。這個“賦予”的過程可以有很多種實現(xiàn),而Python正是其中相對容易上手、同時性能又相當(dāng)不錯的一門語言。本文打算先談?wù)剻C器學(xué)習(xí)相關(guān)的一些比較寬泛的知識,再介紹并說明為何要使用Python來作為機器學(xué)習(xí)的工具。最后,我們會提供一個簡短易懂的、具有實際意義的例子來給大家提供一個直觀的感受。
具體而言,本章主要涉及的知識點有:
機器學(xué)習(xí)的定義及重要性;
Python在機器學(xué)習(xí)領(lǐng)域的優(yōu)異性;
如何在電腦上配置Python機器學(xué)習(xí)的環(huán)境;
機器學(xué)習(xí)一般性的步驟。
機器學(xué)習(xí)緒論
正如前言所說,由于近期的各種最新成果,使得“機器學(xué)習(xí)”成為了非常熱門的詞匯。機器學(xué)習(xí)在各種領(lǐng)域的優(yōu)異表現(xiàn)(圍棋界的Master是其中最具代表性的存在),使得各行各業(yè)的人們都或多或少地對機器學(xué)習(xí)產(chǎn)生了興趣與敬畏。然而與此同時,對機器學(xué)習(xí)有所誤解的群體也日益壯大;他們或?qū)C器學(xué)習(xí)想得過于神秘,或?qū)⑺氲眠^于萬能。本節(jié)擬對機器學(xué)習(xí)進行一般性的介紹,同時會說明機器學(xué)習(xí)中一些常見的術(shù)語以方便之后章節(jié)的敘述。
什么是機器學(xué)習(xí)
清晨的一句“今天天氣真好”、朋友之間的寒暄“你剛剛是去吃飯了吧”、考試過后的感嘆“復(fù)習(xí)了那么久終有收獲”……這些日常生活中隨處可見的話語,其背后卻已蘊含了“學(xué)習(xí)”的思想—它們都是利用以往的經(jīng)驗、對未知的新情況作出的有效的決策。而把這個決策的過程交給計算機來做,可以說就是“機器學(xué)習(xí)”的一個最淺白的定義。
我們或許可以先說說機器學(xué)習(xí)與以往的計算機工作樣式有什么不同。傳統(tǒng)的計算機如果想要得到某個結(jié)果,需要人類賦予它一串實打?qū)嵉闹噶睿缓笥嬎銠C就根據(jù)這串指令一步步地執(zhí)行下去。這個過程中的因果關(guān)系非常明確,只要人類的理解不出偏差,運行結(jié)果是可以準確預(yù)測的。但是在機器學(xué)習(xí)中,這一傳統(tǒng)樣式被打破了:計算機確實仍然需要人類賦予它一串指令,但這串指令往往不能直接得到結(jié)果;相反,它是一串賦予了機器“學(xué)習(xí)能力”的指令。在此基礎(chǔ)上,計算機需要進一步地接受“數(shù)據(jù)”,并根據(jù)之前人類賦予它的“學(xué)習(xí)能力”,從中“學(xué)習(xí)”出最終的結(jié)果。這個結(jié)果往往是無法僅僅通過直接編程得出的。因此這里就導(dǎo)出了稍微深一點的機器學(xué)習(xí)的定義:它是一種讓計算機利用數(shù)據(jù)而非指令來進行各種工作的方法。在這背后,最關(guān)鍵的就是“統(tǒng)計”的思想,它所推崇的“相關(guān)而非因果”的概念是機器學(xué)習(xí)的理論根基。在此基礎(chǔ)上,機器學(xué)習(xí)可以說是計算機使用輸入給它的數(shù)據(jù),利用人類賦予它的算法得到某種模型的過程,其最終的目的則是使用該模型,預(yù)測未來未知數(shù)據(jù)的信息。
既然提到了統(tǒng)計,那么一定的數(shù)學(xué)理論就不可或缺。相關(guān)的、比較簡短的定義會在第4章給出(PAC框架),這里我們就先只敘述機器學(xué)習(xí)在統(tǒng)計理論下的、比較深刻的本質(zhì):它追求的是合理的假設(shè)空間(Hypothesis Space)的選取和模型的泛化(Generalization)能力。該句中出現(xiàn)了一些專用術(shù)語,詳細的定義會在介紹術(shù)語時提及,這里我們提供一個直觀的理解:
所謂的假設(shè)空間,就是我們的模型在數(shù)學(xué)上的“適用場合”。
所謂的泛化能力,就是我們的模型在未知數(shù)據(jù)上的表現(xiàn)。
注意:上述本質(zhì)上嚴格來說,應(yīng)該是PAC Learning的本質(zhì);在其余的理論框架下,機器學(xué)習(xí)是可以具有不同的內(nèi)核的。
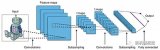
從上面的討論可以看出,機器學(xué)習(xí)和人類思考的過程有或多或少的類似。事實上,我們在第6、第7章講的神經(jīng)網(wǎng)絡(luò)(Neural Network,NN)和卷積神經(jīng)網(wǎng)絡(luò)(Convolutional Neural Network,CNN)背后確實有著相應(yīng)的神經(jīng)科學(xué)的理論背景。然而與此同時需要知道的是,機器學(xué)習(xí)并非是一個“會學(xué)習(xí)的機器人”和“具有學(xué)習(xí)能力的人造人”之類的,這一點從上面諸多討論也可以明晰(慚愧的是,筆者在第一次聽到“機器學(xué)習(xí)”四個字時,腦海中浮現(xiàn)的正是一個“聰明的機器人”的圖像,甚至還幻想過它和人類一起生活的場景)。相反的,它是被人類利用的、用于發(fā)掘數(shù)據(jù)背后信息的工具。
當(dāng)然,現(xiàn)在也不乏“危險的人工智能”的說法,霍金大概是其中的“標桿”,這位偉大的英國理論物理學(xué)家甚至警告說“人工智能的發(fā)展可能意味著人類的滅亡”。孰好孰壞果然還是見仁見智,但可以肯定的是:本書所介紹的內(nèi)容絕不至于導(dǎo)致世界的毀滅,大家大可輕松愉快地進行接下來的閱讀!
機器學(xué)習(xí)常用術(shù)語
機器學(xué)習(xí)領(lǐng)域有著許多非常基本的術(shù)語,這些術(shù)語在外人聽來可能相當(dāng)高深莫測。它們事實上也可能擁有非常復(fù)雜的數(shù)學(xué)背景,但需要知道:它們往往也擁有著相對淺顯平凡的直觀理解(上一小節(jié)的假設(shè)空間和泛化能力就是兩個例子)。本小節(jié)會對這些常用的基本術(shù)語進行說明與解釋,它們背后的數(shù)學(xué)理論會有所闡述,但不會涉及過于本質(zhì)的東西。
正如前文反復(fù)強調(diào)的,數(shù)據(jù)在機器學(xué)習(xí)中發(fā)揮著不可或缺的作用;而用于描述數(shù)據(jù)的術(shù)語有好幾個,需要被牢牢記住的如下。
“數(shù)據(jù)集”(Data Set),就是數(shù)據(jù)的集合的意思。其中,每一條單獨的數(shù)據(jù)被稱為“樣本”(Sample)。若沒有進行特殊說明,本書都會假設(shè)數(shù)據(jù)集中樣本之間在各種意義下相互獨立。事實上,除了某些特殊的模型(如隱馬爾可夫模型和條件隨機場),該假設(shè)在大多數(shù)場景下都是相當(dāng)合理的。
對于每個樣本,它通常具有一些“屬性”(Attribute)或者說“特征”(Feature),特征所具體取的值就被稱為“特征值”(Feature Value)。
特征和樣本所張成的空間被稱為“特征空間”(Feature Space)和“樣本空間”(Sample Space),可以把它們簡單地理解為特征和樣本“可能存在的空間”。
相對應(yīng)的,我們有“標簽空間”(Label Space),它描述了模型的輸出“可能存在的空間”;當(dāng)模型是分類器時,我們通常會稱之為“類別空間”。
其中、數(shù)據(jù)集又可以分為以下三類:
訓(xùn)練集(Training Set);顧名思義,它是總的數(shù)據(jù)集中用來訓(xùn)練我們模型的部分。雖說將所有數(shù)據(jù)集都拿來當(dāng)作訓(xùn)練集也無不可,不過為了提高及合理評估模型的泛化能力,我們通常只會取數(shù)據(jù)集中的一部分來當(dāng)訓(xùn)練集。
測試集(Test Set);顧名思義,它是用來測試、評估模型泛化能力的部分。測試集不會用在模型的訓(xùn)練部分,換句話說,測試集相對于模型而言是“未知”的,所以拿它來評估模型的泛化能力是相當(dāng)合理的。
交叉驗證集(Cross-Validation Set,CV Set);這是比較特殊的一部分數(shù)據(jù),它是用來調(diào)整模型具體參數(shù)的。
注意:需要指出的是,獲取數(shù)據(jù)集這個過程是不平凡的;尤其是當(dāng)今“大數(shù)據(jù)”如日中天的情景下,諸如“得數(shù)據(jù)者得天下”的說法也不算誑語。在此筆者推薦一個非常著名的含有大量真實數(shù)據(jù)集的網(wǎng)站: ,本書常常會用到其中一些合適的數(shù)據(jù)集來評估我們自己實現(xiàn)的模型。
可以通過具體的例子來理解上述概念。比如,我們假設(shè)小明是一個在北京讀了一年書的學(xué)生,某天他想通過宿舍窗外的風(fēng)景(能見度、溫度、濕度、路人戴口罩的情況等)來判斷當(dāng)天的霧霾情況并據(jù)此決定是否戴口罩。此時,他過去一年的經(jīng)驗就是他擁有的數(shù)據(jù)集,過去一年中每一天的情況就是一個樣本。“能見度”、“溫度”、“濕度”、“路人戴口罩的情況”就是四個特征,而(能見度)“低”、(溫度)“低”、(濕度)“高”、(路人戴口罩的)“多”就是相對應(yīng)的特征值。現(xiàn)在小明想了想,決定在腦中建立一個模型來幫自己做決策,該模型將利用過去一年的數(shù)據(jù)集來對如今的情況做出“是否戴口罩”的決策。此時小明可以用過去一年中8個月的數(shù)據(jù)量來做訓(xùn)練集、2個月的量來做測試集、2個月的量來做交叉驗證集,那么小明就需要不斷地思考(訓(xùn)練模型)下列問題:
用訓(xùn)練集訓(xùn)練出的模型是怎樣的?
該模型在交叉驗證集上的表現(xiàn)怎么樣?
. 如果足夠好了,那么思考結(jié)束(得到最終模型)。
. 如果不夠好,那么根據(jù)模型在交叉驗證集上的表現(xiàn),重新思考(調(diào)整模型參數(shù))
最后,小明可能會在測試集上評估自己剛剛思考后得到的模型的性能,然后根據(jù)這個性能和模型做出的“是否戴口罩”的決策來綜合考慮自己到底戴不戴口罩。
接下來說明上一小節(jié)中提到過的重要概念:假設(shè)空間與泛化能力。泛化能力的含義在上文也有說明,為強調(diào)起見,這里再敘述一遍:
泛化能力針對的其實是學(xué)習(xí)方法,它用于衡量該學(xué)習(xí)方法學(xué)習(xí)到的模型在整個樣本空間上的表現(xiàn)。
這一點當(dāng)然是十分重要的,因為我們拿來訓(xùn)練模型的數(shù)據(jù)終究只是樣本空間的一個很小的采樣,如果只是過分專注于它們,就會出現(xiàn)所謂的“過擬合”(Over Fitting)的情況。當(dāng)然,如果過分罔顧訓(xùn)練數(shù)據(jù),又會出現(xiàn)“欠擬合”(Under Fitting)。可以用一張圖來直觀地感受過擬合和欠擬合(如圖1所示,左為欠擬合,右為過擬合)。

圖1 欠擬合與過擬合
所以需要“張弛有度”,找到最好的那個平衡點。統(tǒng)計學(xué)習(xí)中的結(jié)構(gòu)風(fēng)險最小化(Structural Risk Minimization,SRM)就是研究這個的,它和傳統(tǒng)的經(jīng)驗風(fēng)險最小化(Empirical Risk Minimization,ERM)相比,注重于對風(fēng)險上界的最小化,而不是單純地使經(jīng)驗風(fēng)險最小化。它有一個原則:在使風(fēng)險上界最小的函數(shù)子集中挑選出使經(jīng)驗風(fēng)險最小的函數(shù)。而這個函數(shù)子集,正是我們之前提到過的假設(shè)空間。
注意:所謂經(jīng)驗風(fēng)險,可以理解為訓(xùn)練數(shù)據(jù)集上的風(fēng)險。相對應(yīng)的,ERM則可以理解為只注重訓(xùn)練數(shù)據(jù)集的學(xué)習(xí)方法,它的理論基礎(chǔ)是經(jīng)驗風(fēng)險在某種足夠合理的數(shù)學(xué)意義上一致收斂于期望風(fēng)險,亦即所謂的“真正的”風(fēng)險。
關(guān)于SRM和ERM的詳細討論會涉及諸如VC維和正則化的概念,這里不進行詳細展開,但需要有這么一個直觀的認識:為了使我們學(xué)習(xí)方法訓(xùn)練出的模型泛化能力足夠好,需要對模型做出一定的“限制”,而這個“限制”就表現(xiàn)在假設(shè)空間的選取上。一個非常普遍的做法是對模型的復(fù)雜度做出一定的懲罰,從而使模型趨于精簡。這與所謂的“奧卡姆剃刀原理”不謀而合:“如無必要,勿增實體”“切勿浪費較多的東西去做,用較少的東西、同樣可以做好事情”。
相比起通過選取合適的假設(shè)空間來規(guī)避過擬合,進行交叉驗證(Cross Validation)則可以讓我們知道過擬合的程度,從而幫助我們選擇合適的模型。常見的交叉驗證有以下三種。
S-fold Cross Validation:中文可翻譯成S折交叉驗證,它是應(yīng)用最多的一種方法,其方法大致如下。
. 將數(shù)據(jù)分成S份:D={D_1,D_2,…,D_S},一共做S次試驗。
. 在第i次試驗中,使用D-D_i作為訓(xùn)練集,D_i作為測試集對模型進行訓(xùn)練和評測。
. 最終選擇平均測試誤差最小的模型。
留一交叉驗證(Leave-one-out Cross Validation):這是S折交叉驗證的特殊情況,此時S=N。
簡易交叉驗證:這種實現(xiàn)起來最簡單,也是本書(在進行交叉驗證時)所采用的方法。它簡單地將數(shù)據(jù)進行隨機分組,最后達到訓(xùn)練集約占原數(shù)據(jù)70%的程度(這個比例可以視情況改變),選擇模型時使用測試誤差作為標準。
機器學(xué)習(xí)的重要性
道理說了不少,但到底為什么要學(xué)機器學(xué)習(xí),機器學(xué)習(xí)的重要性又在哪里呢?事實上,回顧歷史可以發(fā)現(xiàn),人類的發(fā)展通常伴隨著簡單體力勞動向復(fù)雜腦力勞動的過渡。過去的工作基本上都有著明確的定義,告訴你這一步怎么做、下一步再怎么做。而如今這一類的工作已經(jīng)越來越少,取而代之的是更為寬泛模糊的、概念性的東西,比如說“將本季度的產(chǎn)品推向最合適的市場,在最大化期望利潤的同時,盡量做到風(fēng)險最小化”這種需求。想要完成好這樣的任務(wù),需要獲取相應(yīng)的數(shù)據(jù);雖說網(wǎng)絡(luò)的存在讓我們能夠得到數(shù)之不盡的數(shù)據(jù),然而從這些數(shù)據(jù)中獲得信息與知識卻不是一項簡單的工作。我們當(dāng)然可以人工地、仔細地逐項甄選,但這樣顯然就又回到了最初的原點。機器學(xué)習(xí)這門技術(shù),可以說正因此應(yīng)運而生。
單單抽象地說一大堆空話可能會讓人頭昏腦漲,我們就舉一舉機器學(xué)習(xí)具體的應(yīng)用范圍,從中大概能夠比較直觀地看出機器學(xué)習(xí)的強大與重要。
發(fā)展到如今,機器學(xué)習(xí)的“爪牙”可謂已經(jīng)伸展到了各個角落、包括但不限于:
機器視覺,也就是最近機器學(xué)習(xí)里很火熱的深度學(xué)習(xí)的一種應(yīng)用;
語音識別,也就是微軟Cortana背后的核心技術(shù);
數(shù)據(jù)挖掘,也就是耳熟能詳?shù)拇髷?shù)據(jù)相關(guān)的領(lǐng)域;
統(tǒng)計學(xué)習(xí),也就是本書講解的主要范圍之一,有許許多多著名的算法(比如支持向量機SVM)都源于統(tǒng)計學(xué)習(xí)(但是統(tǒng)計學(xué)習(xí)還是和機器學(xué)習(xí)有區(qū)別的;簡單地說,統(tǒng)計學(xué)習(xí)偏數(shù)學(xué)而機器學(xué)習(xí)偏實踐)。
機器學(xué)習(xí)還能夠進行模式識別、自然語言處理,等等,之前提到過的圍棋界的Master和最新人工智能在德州撲克上的表現(xiàn)亦無不呈現(xiàn)著機器學(xué)習(xí)強大的潛力。一言以蔽之,機器學(xué)習(xí)是當(dāng)今的熱點,雖說不能保證它的熱度能100%地一直延續(xù)下去,至少筆者認為、它能在相當(dāng)長的一段時間內(nèi)保持強大的生命力。
人生苦短,我用Python
上一節(jié)大概地介紹了機器學(xué)習(xí)的各種概念,這一節(jié)我們主要講講腳本語言Python相關(guān)的一些東西。題目是在Python界流傳甚廣的“諺語”,它講述了Python強大的功能與易于上手的特性。
為何選擇Python
援引開源運動的領(lǐng)袖人物Eric Raymond的說法:“Python語言非常干凈,設(shè)計優(yōu)雅,具有出色的模塊化特性。其最出色的地方在于,鼓勵清晰易讀的代碼,特別適合以漸進開發(fā)的方式構(gòu)造項目”。Python的可讀性使得即使是剛學(xué)不久的人也能看懂大部分的代碼,Python龐大的社區(qū)和大量的開發(fā)文檔更是使得初學(xué)者能夠快速地實現(xiàn)許許多多令人驚嘆的功能。對于Python的程序,人們甚至有時會戲稱其為“可執(zhí)行的偽代碼(executable pseudo-code)”,以突顯它的清晰性和可讀性。
Python的強大是毋庸置疑的,上文提到的Eric Raymond甚至稱其“過于強大了”。與之相對應(yīng)的,就是Python的速度比較慢。然而比起Python開發(fā)環(huán)境提供的海量高級數(shù)據(jù)結(jié)構(gòu)(如列表、元組、字典、集合等)和數(shù)之不盡的第三方庫,再加上高速的CPU和近代發(fā)展起來的GPU編程,速度的問題就顯得沒那么尖銳了。況且Python還能通過各種途徑使用C / C++代碼來編寫核心代碼,其強大的“膠水”功能使其速度(在程序員能力允許的情況下)和純粹的C / C++相比已經(jīng)相去不遠。一個典型的例子,也是我們會在本書常常運用到的Python中Numpy這個第三方庫。編寫它的語言正是底層語言(C和Fortran),其支持向量、矩陣操作的特性和優(yōu)異的速度,使得Python在科學(xué)計算這一領(lǐng)域大放異彩。
注意:Python及本書用到的兩個非常優(yōu)異的第三方庫—Numpy和TensorFlow的簡要教程我們會作為附錄章節(jié)放在本書的最后,建議有需要的讀者先閱讀相應(yīng)部分。
Python 在機器學(xué)習(xí)領(lǐng)域的優(yōu)勢
雖然在上一小節(jié)敘述了Python的種種好處,但不可否認的是,確實存在諸如MATLAB和Mathematica這樣的高級程序語言。它們對機器學(xué)習(xí)的支持也不錯,MATLAB甚至還自帶許多機器學(xué)習(xí)的應(yīng)用。但是作為一個問心無愧的程序員,我們還是需要提倡支持正版,而MATLAB的正版軟件需要花費數(shù)千美元。與之相對,由于Python是開源項目,幾乎所有必要的組件都是完全免費的。
之前也提到過Python的速度問題,但是更快更底層的語言,比如C和C++,若使用它們來學(xué)習(xí)機器學(xué)習(xí),會不可避免地引發(fā)這么一個問題:即使是實現(xiàn)一個非常簡單的功能,也需要進行大量的編寫和調(diào)試的過程;在這期間,程序員很有可能忘掉學(xué)習(xí)機器學(xué)習(xí)的初衷而迷失在代碼的海洋中。筆者曾經(jīng)嘗試過將Python上的神經(jīng)網(wǎng)絡(luò)框架移植到C++上,這之間的折騰至今難忘。
此外,筆者認為、使用Python來學(xué)習(xí)機器學(xué)習(xí)是和“不要過早優(yōu)化”這句編程界的金句有著異曲同工之妙的。Python(幾乎)唯一的缺陷—速度,在初期進行快速檢驗算法、思想正誤及開發(fā)工作時,其實基本上不是重要問題。其中的道理是顯而易見的:如果解決問題的思想存在問題,那么即使拼命去提高程序的運行效率,也只能使問題越來越大而已。這種時候,先使用Python進行快速實現(xiàn),有必要時再用底層代碼重寫核心代碼,從各方面來說都是一個更好的選擇。
關(guān)于Anaconda
Python的強大有相當(dāng)大一部分體現(xiàn)在它那浩如煙海的第三方庫。在使用Python實現(xiàn)一個復(fù)雜功能時,如果沒有特殊的需求,我們通常會先搜索Google有沒有現(xiàn)成的第三方庫,然后會搜索是否有相關(guān)聯(lián)的第三方庫,最后才會考慮自己重頭實現(xiàn)。
第三方庫是如此之多,從中挑選出心儀而合適的并非易事。幸運的是,就連這一點也有第三方軟件進行了支持,那就是在Python科學(xué)計算領(lǐng)域非常出名的Anaconda。這是一個完全免費的軟件,經(jīng)常會進行各種更新;最重要的是,它把幾乎所有常用且優(yōu)異的科學(xué)計算庫都集成在了一起。換句話說,只要你安裝了Anaconda,就意味著擁有了一個完善精致的機器學(xué)習(xí)環(huán)境,基本上無須自己把要用到的庫一個一個通過命令行來安裝。
第一個機器學(xué)習(xí)樣例
作為本章的總結(jié),我們來運用Python解決一個實際問題,以便對機器學(xué)習(xí)有一個具體的感受。由于該樣例只是為了提供直觀感受,我們就拿比較有名的一個小問題來進行闡述。俗話說:“麻雀雖小,五臟俱全”,我們完全可以通過這個樣例來對機器學(xué)習(xí)的一般性步驟進行一個大致的認知。
該問題來自Coursera上的斯坦福大學(xué)機器學(xué)習(xí)課程,其敘述如下:現(xiàn)有47個房子的面積和價格,需要建立一個模型對新的房價進行預(yù)測。稍微翻譯問題,可以得知:
輸入數(shù)據(jù)只有一維,亦即房子的面積。
目標數(shù)據(jù)也只有一維,亦即房子的價格。
需要做的,就是根據(jù)已知的房子的面積和價格的關(guān)系進行機器學(xué)習(xí)。
下面我們就來一步步地進行操作。
獲取與處理數(shù)據(jù)
原始數(shù)據(jù)集的前10個樣本如表1.1所示,這里房子面積和房子價格的單位可以隨意定奪,因為它們不會對結(jié)果造成影響。
表1.1 房價數(shù)據(jù)集

完整的數(shù)據(jù)集可以參見 https://github.com/carefree0910/MachineLearning/blob/master/ _Data/prices.txt 。雖然該數(shù)據(jù)集比較簡單,但可以看到其中的數(shù)字都相當(dāng)大。保留它原始形式確實有可能是有必要的,但一般而言,我們應(yīng)該對它做簡單的處理以期望降低問題的復(fù)雜度。在這個例子里,采取常用的將輸入數(shù)據(jù)標準化的做法,其數(shù)學(xué)公式為:

代碼1-1 第一個機器學(xué)習(xí)樣例:a_FirstExample\Regression.py
01 # 導(dǎo)入需要用到的庫
02 import numpy as np
03 import matplotlib.pyplot as plt
04
05 # 定義存儲輸入數(shù)據(jù)(x)和目標數(shù)據(jù)(y)的數(shù)組
06 x, y = [], []
07 # 遍歷數(shù)據(jù)集,變量sample對應(yīng)的正是一個個樣本
08 for sample in open("../_Data/prices.txt", "r"):
09 # 由于數(shù)據(jù)是用逗號隔開的,所以調(diào)用Python中的split方法并將逗號作為參數(shù)傳入
10 _x, _y = sample.split(",")
11 # 將字符串?dāng)?shù)據(jù)轉(zhuǎn)化為浮點數(shù)
12 x.append(float(_x))
13 y.append(float(_y))
14 # 讀取完數(shù)據(jù)后,將它們轉(zhuǎn)化為Numpy數(shù)組以方便進一步的處理
15 x, y = np.array(x), np.array(y)
16 # 標準化
17 x = (x - x.mean()) / x.std()
18 # 將原始數(shù)據(jù)以散點圖的形式畫出
19 plt.figure()
20 plt.scatter(x, y, c="g", s=6)
21 plt.show()
上面這段代碼的運行結(jié)果如圖2所示。

圖2 預(yù)處理后的數(shù)據(jù)散點圖
這里橫軸是標準化后的房子面積,縱軸是房子價格。以上我們已經(jīng)比較好地完成了機器學(xué)習(xí)任務(wù)的第一步:數(shù)據(jù)預(yù)處理。
選擇與訓(xùn)練模型
在弄好數(shù)據(jù)之后,下一步就要開始選擇相應(yīng)的學(xué)習(xí)方法和模型了。幸運的是,通過可視化原始數(shù)據(jù),可以非常直觀地感受到:很有可能通過線性回歸(Linear Regression)中的多項式擬合來得到一個不錯的結(jié)果。其模型的數(shù)學(xué)表達式如下。
注意:用多項式擬合散點只是線性回歸的很小的一部分,但是它的直觀意義比較明顯。考慮到問題比較簡單,我們才選用了多項式擬合。線性回歸的詳細討論超出了本書的范圍,這里不再贅述。

其中f(x|p;n)就是我們的模型,p、n都是模型的參數(shù),其中p是多項式f的各個系數(shù),n是多項式的次數(shù)。L(p;n)則是模型的損失函數(shù),這里我們采用了常見的平方損失函數(shù),也就是所謂的歐氏距離(或說向量的二范數(shù))。x、y則分別是輸入向量和目標向量;在我們這個樣例中,x、y這兩個向量都是47維的向量,分別由47個不同的房子面積、房子價格所構(gòu)成。
在確定好模型后,就可以開始編寫代碼來進行訓(xùn)練了。對于大多數(shù)機器學(xué)習(xí)算法,所謂的訓(xùn)練正是最小化某個損失函數(shù)的過程,這個多項式擬合的模型也不例外:我們的目的就是讓上面定義的L(p;n)最小。在數(shù)理統(tǒng)計領(lǐng)域里有專門的理論研究這種回歸問題,其中比較有名的正規(guī)方程更是直接給出了一個簡單的解的通式。不過由于有Numpy的存在,這個訓(xùn)練過程甚至變得還要更加簡單一些。
22 # 在(-2,4)這個區(qū)間上取100個點作為畫圖的基礎(chǔ)
23 x0 = np.linspace(-2, 4, 100)
24 # 利用Numpy的函數(shù)定義訓(xùn)練并返回多項式回歸模型的函數(shù)
25 # deg參數(shù)代表著模型參數(shù)中的n,亦即模型中多項式的次數(shù)
26 # 返回的模型能夠根據(jù)輸入的x(默認是x0),返回相對應(yīng)的預(yù)測的y
27 def get_model(deg):
28 return lambda input_x=x0: np.polyval(np.polyfit(x, y, deg), input_x)
這里需要解釋Numpy里面帶的兩個函數(shù):polyfit和polyval的用法。
polyfit(x, y, deg):該函數(shù)會返回使得上述
(注:該公式中的x和y就是輸入的x和y)最小的參數(shù)p,亦即多項式的各項系數(shù)。換句話說,該函數(shù)就是模型的訓(xùn)練函數(shù)。
polyval(p, x):根據(jù)多項式的各項系數(shù)p和多項式中x的值,返回多項式的值y。
29 # 根據(jù)參數(shù)n、輸入的x、y返回相對應(yīng)的損失
30 def get_cost(deg, input_x, input_y):
31 return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
32 # 定義測試參數(shù)集并根據(jù)它進行各種實驗
33 test_set = (1, 4, 10)
34 for d in test_set:
35 # 輸出相應(yīng)的損失
36 print(get_cost(d, x, y))
所得的結(jié)果是:當(dāng)n=1,4,10時,損失的頭兩位數(shù)字分別為96、94和75。這么看來似乎是n=10優(yōu)于n=4,而n=1最差,但從圖3可以看出,似乎直接選擇n=1作為模型的參數(shù)才是最好的選擇。這里矛盾的來源正是前文所提到過的過擬合情況。

圖3 線性回歸的可視化
那么,怎么最直觀地了解是否出現(xiàn)過擬合了呢?當(dāng)然還是畫圖了。
37 # 畫出相應(yīng)的圖像
38 plt.scatter(x, y, c="g", s=20)
39 for d in test_set:
40 plt.plot(x0, get_model(d)(), label="degree = {}".format(d))
41 # 將橫軸、縱軸的范圍分別限制在(-2,4)、(〖10〗^5,8×〖10〗^5)
42 plt.xlim(-2, 4)
43 plt.ylim(1e5, 8e5)
44 # 調(diào)用legend方法使曲線對應(yīng)的label正確顯示
45 plt.legend()
46 plt.show()
上面這段代碼的運行結(jié)果如圖3所示。
其中,三條線分別代表n=1、n=4、n=10的情況(圖1.10的右上角亦有說明)。可以看出,從n=4開始模型就已經(jīng)開始出現(xiàn)過擬合現(xiàn)象了,到n=10時模型已經(jīng)變得非常不合理。
至此,可以說這個問題就已經(jīng)基本上解決了。在這個樣例里面,除了交叉驗證,我們涵蓋了機器學(xué)習(xí)中的大部分主要步驟(之所以沒有進行交叉驗證是因為數(shù)據(jù)太少了……)。代碼部分加起來總共40~50行,應(yīng)該算是一個比較合適的長度。希望大家能夠通過這個樣例對機器學(xué)習(xí)有個大概的了解,也希望它能引起大家對機器學(xué)習(xí)的興趣。
本章小結(jié)
與傳統(tǒng)的計算機程序不同,機器學(xué)習(xí)是面向數(shù)據(jù)的算法,能夠從數(shù)據(jù)中獲得信息。它符合新時代腦力勞動代替體力勞動的趨勢,是富有生命力的領(lǐng)域。
Python是一門優(yōu)異的語言,代碼清晰可讀、功能廣泛強大。其最大弱點—速度問題也可以通過很多不太困難的方法彌補。
Anaconda是Python的一個很好的集成環(huán)境,它能讓我們免于人工地安裝大量科學(xué)計算所需要的第三方庫。
雖說機器學(xué)習(xí)算法很多,但通常而言,進行機器學(xué)習(xí)的過程會包含以下三步:
. 獲取與處理數(shù)據(jù);
. 選擇與訓(xùn)練模型;
. 評估與可視化結(jié)果。
 電子發(fā)燒友App
電子發(fā)燒友App
























評論