摘要: 本文對多層感知器和反向傳播進行入門級的介紹。 人工神經網絡是一種計算模型,啟發自人類大腦處理信息的生物神經網絡。
人工神經網絡是一種計算模型,啟發自人類大腦處理信息的生物神經網絡。人工神經網絡在語音識別、計算機視覺和文本處理領域取得了一系列突破,讓機器學習研究和產業感到了興奮。在本篇博文中,我們將試圖理解一種稱為「多層感知器(Multi Layer Perceptron)」的特定的人工神經網絡。
?
單個神經元
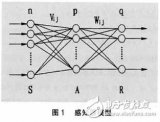
神經網絡中計算的基本單元是神經元,一般稱作「節點」(node)或者「單元」(unit)。節點從其他節點接收輸入,或者從外部源接收輸入,然后計算輸出。每個輸入都輔有「權重」(weight,即 w),權重取決于其他輸入的相對重要性。節點將函數 f(定義如下)應用到加權后的輸入總和,如圖 1 所示:

圖 1:單個神經元
此網絡接受 X1 和 X2 的數值輸入,其權重分別為 w1 和 w2。另外,還有配有權重 b(稱為「偏置(bias)」)的輸入 1。我們之后會詳細介紹「偏置」的作用。
神經元的輸出 Y 如圖 1 所示進行計算。函數 f 是非線性的,叫做激活函數。激活函數的作用是將非線性引入神經元的輸出。因為大多數現實世界的數據都是非線性的,我們希望神經元能夠學習非線性的函數表示,所以這種應用至關重要。
每個(非線性)激活函數都接收一個數字,并進行特定、固定的數學計算 [2]。在實踐中,可能會碰到幾種激活函數:
Sigmoid(S 型激活函數):輸入一個實值,輸出一個 0 至 1 間的值 σ(x) = 1 / (1 + exp(?x))
tanh(雙曲正切函數):輸入一個實值,輸出一個 [-1,1] 間的值 tanh(x) = 2σ(2x) ? 1
ReLU:ReLU 代表修正線性單元。輸出一個實值,并設定 0 的閾值(函數會將負值變為零)f(x) = max(0, x)
下圖 [2] 表示了上述的激活函數

圖 2:不同的激活函數。
偏置的重要性:偏置的主要功能是為每一個節點提供可訓練的常量值(在節點接收的正常輸入以外)。神經元中偏置的作用,詳見這個鏈接:
前饋神經網絡
前饋神經網絡是最先發明也是最簡單的人工神經網絡 [3]。它包含了安排在多個層中的多個神經元(節點)。相鄰層的節點有連接或者邊(edge)。所有的連接都配有權重。
圖 3 是一個前饋神經網絡的例子。

圖 3: 一個前饋神經網絡的例子
一個前饋神經網絡可以包含三種節點:
1. 輸入節點(Input Nodes):輸入節點從外部世界提供信息,總稱為「輸入層」。在輸入節點中,不進行任何的計算——僅向隱藏節點傳遞信息。
2. 隱藏節點(Hidden Nodes):隱藏節點和外部世界沒有直接聯系(由此得名)。這些節點進行計算,并將信息從輸入節點傳遞到輸出節點。隱藏節點總稱為「隱藏層」。盡管一個前饋神經網絡只有一個輸入層和一個輸出層,但網絡里可以沒有也可以有多個隱藏層。
3. 輸出節點(Output Nodes):輸出節點總稱為「輸出層」,負責計算,并從網絡向外部世界傳遞信息。
在前饋網絡中,信息只單向移動——從輸入層開始前向移動,然后通過隱藏層(如果有的話),再到輸出層。在網絡中沒有循環或回路 [3](前饋神經網絡的這個屬性和遞歸神經網絡不同,后者的節點連接構成循環)。
下面是兩個前饋神經網絡的例子:
1. 單層感知器——這是最簡單的前饋神經網絡,不包含任何隱藏層。你可以在 [4] [5] [6] [7] 中了解更多關于單層感知器的知識。
2. 多層感知器——多層感知器有至少一個隱藏層。我們在下面會只討論多層感知器,因為在現在的實際應用中,它們比單層感知器要更有用。
多層感知器
多層感知器(Multi Layer Perceptron,即 MLP)包括至少一個隱藏層(除了一個輸入層和一個輸出層以外)。單層感知器只能學習線性函數,而多層感知器也可以學習非線性函數。

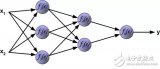
圖 4:有一個隱藏層的多層感知器
圖 4 表示了含有一個隱藏層的多層感知器。注意,所有的連接都有權重,但在圖中只標記了三個權重(w0,,w1,w2)。
輸入層:輸入層有三個節點。偏置節點值為 1。其他兩個節點從 X1 和 X2 取外部輸入(皆為根據輸入數據集取的數字值)。和上文討論的一樣,在輸入層不進行任何計算,所以輸入層節點的輸出是 1、X1 和 X2 三個值被傳入隱藏層。
隱藏層:隱藏層也有三個節點,偏置節點輸出為 1。隱藏層其他兩個節點的輸出取決于輸入層的輸出(1,X1,X2)以及連接(邊界)所附的權重。圖 4 顯示了隱藏層(高亮)中一個輸出的計算。其他隱藏節點的輸出計算同理。需留意 *f *指代激活函數。這些輸出被傳入輸出層的節點。
輸出層:輸出層有兩個節點,從隱藏層接收輸入,并執行類似高亮出的隱藏層的計算。這些作為計算結果的計算值(Y1 和 Y2)就是多層感知器的輸出。
給出一系列特征 X = (x1, x2, ...) 和目標 Y,一個多層感知器可以以分類或者回歸為目的,學習到特征和目標之間的關系。
為了更好的理解多層感知器,我們舉一個例子。假設我們有這樣一個學生分數數據集:

兩個輸入欄表示了學生學習的時間和期中考試的分數。最終結果欄可以有兩種值,1 或者 0,來表示學生是否通過的期末考試。例如,我們可以看到,如果學生學習了 35 個小時并在期中獲得了 67 分,他 / 她就會通過期末考試。
現在我們假設我們想預測一個學習了 25 個小時并在期中考試中獲得 70 分的學生是否能夠通過期末考試。
這是一個二元分類問題,多層感知器可以從給定的樣本(訓練數據)進行學習,并且根據給出的新的數據點,進行準確的預測。在下面我們可以看到一個多層感知器如何學習這種關系。
訓練我們的多層感知器:反向傳播算法
反向傳播誤差,通常縮寫為「BackProp」,是幾種訓練人工神經網絡的方法之一。這是一種監督學習方法,即通過標記的訓練數據來學習(有監督者來引導學習)。
簡單說來,BackProp 就像「從錯誤中學習」。監督者在人工神經網絡犯錯誤時進行糾正。
一個人工神經網絡包含多層的節點;輸入層,中間隱藏層和輸出層。相鄰層節點的連接都有配有「權重」。學習的目的是為這些邊緣分配正確的權重。通過輸入向量,這些權重可以決定輸出向量。
在監督學習中,訓練集是已標注的。這意味著對于一些給定的輸入,我們知道期望 / 期待的輸出(標注)。
反向傳播算法:最初,所有的邊權重(edge weight)都是隨機分配的。對于所有訓練數據集中的輸入,人工神經網絡都被激活,并且觀察其輸出。這些輸出會和我們已知的、期望的輸出進行比較,誤差會「傳播」回上一層。該誤差會被標注,權重也會被相應的「調整」。該流程重復,直到輸出誤差低于制定的標準。
上述算法結束后,我們就得到了一個學習過的人工神經網絡,該網絡被認為是可以接受「新」輸入的。該人工神經網絡可以說從幾個樣本(標注數據)和其錯誤(誤差傳播)中得到了學習。
現在我們知道了反向傳播的原理,我們回到上面的學生分數數據集。

圖 5:多層感知器的前向傳播
圖 5 中的多層感知器(修改自 Sebastian Raschka 漂亮的反向傳播算法圖解:https://github.com/rasbt/python-machine-learning-book/blob/master/faq/visual-backpropagation.md)的輸入層有兩個節點(除了偏置節點以外),兩個節點分別接收「學習小時數」和「期中考試分數」。感知器也有一個包含兩個節點的隱藏層(除了偏置節點以外)。輸出層也有兩個節點——上面一個節點輸出「通過」的概率,下面一個節點輸出「不通過」的概率。
在分類任務中,我們通常在感知器的輸出層中使用 Softmax 函數作為激活函數,以保證輸出的是概率并且相加等于 1。Softmax 函數接收一個隨機實值的分數向量,轉化成多個介于 0 和 1 之間、并且總和為 1 的多個向量值。所以,在這個例子中:
概率(Pass)+概率(Fail)=1
第一步:前向傳播
網絡中所有的權重都是隨機分配的。我們現在考慮圖 5 中標注 V 的隱藏層節點。假設從輸入連接到這些節點的權重分別為 w1、w2 和 w3(如圖所示)。
神經網絡會將第一個訓練樣本作為輸入(我們已知在輸入為 35 和 67 的情況下,通過的概率為 1)。
網絡的輸入=[35, 67]
期望的網絡輸出(目標)=[1, 0]
涉及到的節點的輸出 V 可以按如下方式計算(*f* 是類似 Sigmoid 的激活函數):
V = f(1*w1 + 35*w2 + 67*w3)
同樣,隱藏層的其他節點的輸出也可以計算。隱藏層兩個節點的輸出,是輸出層兩個節點的輸入。這讓我們可以計算輸出層兩個輸出的概率值。
假設輸出層兩個節點的輸出概率分別為 0.4 和 0.6(因為權重隨機,輸出也會隨機)。我們可以看到計算后的概率(0.4 和 0.6)距離期望概率非常遠(1 和 0),所以圖 5 中的網絡被視為有「錯誤輸出」。
第二步:反向傳播和權重更新
我們計算輸出節點的總誤差,并將這些誤差用反向傳播算法傳播回網絡,以計算梯度。接下來,我們使用類似梯度下降之類的算法來「調整」網絡中的所有權重,目的是減少輸出層的誤差。圖 6 展示了這一過程(暫時忽略圖中的數學等式)。
假設附給節點的新權重分別是 w4,w5 和 w6(在反向傳播和權重調整之后)。

圖 6:多層感知器中的反向傳播和權重更新步驟
如果我們現在再次向網絡輸入同樣的樣本,網絡應該比之前有更好的表現,因為為了最小化誤差,已經調整了權重。如圖 7 所示,和之前的 [0.6, -0.4] 相比,輸出節點的誤差已經減少到了 [0.2, -0.2]。這意味著我們的網絡已經學習了如何正確對第一個訓練樣本進行分類。

圖 7:在同樣的輸入下,多層感知器網絡有更好的表現
用我們數據集中的其他訓練樣本來重復這一過程。這樣,我們的網絡就可以被視為學習了這些例子。
現在,如果我們想預測一個學習了 25 個小時、期中考試 70 分的學生是否能通過期末考試,我們可以通過前向傳播步驟來計算 Pass 和 Fail 的輸出概率。
我回避了數學公式和類似「梯度下降(Gradient Descent)」之類概念的解釋,而是培養了一種對于算法的直覺。對于反向傳播算法更加注重數學方面討論,請參加此鏈接: ~vlsi/AI/backp_t_en/backprop.html
多層感知器的 3D 可視化
Adam Harley 創造了一個多層感知器的 3D 可視化(~aharley/vis/fc/),并已經開始使用 MNIST 數據庫手寫的數字進行訓練。
此網絡從一個 28 x 28 的手寫數字圖像接受 784 個數字像素值作為輸入(在輸入層有對應的 784 個節點)。網絡的第一個隱藏層有 300 個節點,第二個隱藏層有 100 個節點,輸出層有 10 個節點(對應 10 個數字)[15]。
雖然這個網絡跟我們剛才討論的相比大了很多(使用了更多的隱藏層和節點),所有前向傳播和反向傳播步驟的計算(對于每個節點而言)方式都是一樣的。
圖 8 顯示了輸入數字為「5」的時候的網絡
圖 8:輸入為「5」時的視覺化的網絡
輸出值比其它節點高的節點,用更亮的顏色表示。在輸入層,更亮的節點代表接受的數字像素值更高。注意,在輸出層,亮色的節點是如何代表數字 5 的(代表輸出概率為 1,其他 9 個節點的輸出概率為 0)。這意味著多層感知器對輸入數字進行了正確的分類。我非常推薦對這個可視化進行探究,觀察不同節點之間的聯系。
結論
在這篇文章中,我跳過了部分概念的重要細節,以促進理解。為了全面理解多層感知器,我推薦閱讀斯坦福神經網絡教程的第一、第二、第三和案例研究部分。如果有任何問題或者建議,請在下方評論告訴我。
 電子發燒友App
電子發燒友App











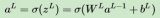












評論