摘要：本文展示了如何基于nolearn使用一些卷積層和池化層來建立一個簡單的ConvNet體系結構，以及如何使用ConvNet去訓練一個特征提取器，然后在使用如SVM、Logistic回歸等不同的模型之前使用它來進行特征提取。
?

卷積神經網絡（ConvNets）是受生物啟發的MLPs（多層感知器），它們有著不同類別的層，并且每層的工作方式與普通的MLP層也有所差異。如果你對ConvNets感興趣，這里有個很好的教程CS231n?–?Convolutional?Neural?Newtorks?for?Visual?Recognition。CNNs的體系結構如下所示：

常規的神經網絡

ConvNet網絡體系結構

如你所見，ConvNets工作時伴隨著3D卷積并且在不斷轉變著這些3D卷積。我在這篇文章中不會再重復整個CS231n的教程，所以如果你真的感興趣，請在繼續閱讀之前先花點時間去學習一下。

Lasagne 和 nolearn

Lasagne和nolearn是我最喜歡使用的深度學習Python包。Lasagne是基于Theano的，所以GPU的加速將大有不同，并且其對神經網絡創建的聲明方法也很有幫助。nolearn庫是一個神經網絡軟件包實用程序集（包含Lasagne），它在神經網絡體系結構的創建過程上、各層的檢驗等都能夠給我們很大的幫助。

在這篇文章中我要展示的是，如何使用一些卷積層和池化層來建立一個簡單的ConvNet體系結構。我還將向你展示如何使用ConvNet去訓練一個特征提取器，在使用如SVM、Logistic回歸等不同的模型之前使用它來進行特征提取。大多數人使用的是預訓練ConvNet模型，然后刪除最后一個輸出層，接著從ImageNets數據集上訓練的ConvNets網絡提取特征。這通常被稱為是遷移學習，因為對于不同的問題你可以使用來自其它的ConvNets層，由于ConvNets的第一層過濾器被當做是一個邊緣探測器，所以它們可以用來作為其它問題的普通特征探測器。

加載MNIST數據集

MNIST數據集是用于數字識別最傳統的數據集之一。我們使用的是一個面向Python的版本，但先讓我們導入需要使用的包：
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from urllib import urlretrieve
import cPickle as pickle
import os
import gzip
import numpy as np
import theano
import lasagne
from lasagne import layers
from lasagne.updates import nesterov_momentum
from nolearn.lasagne import NeuralNet
from nolearn.lasagne import visualize
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix

正如你所看到的，我們導入了用于繪圖的matplotlib包，一些用于下載MNIST數據集的原生Python模塊，numpy， theano，lasagne，nolearn 以及 scikit-learn庫中用于模型評估的一些函數。

然后，我們定義一個加載MNIST數據集的函數（這個功能與Lasagne教程上使用的非常相似）
def load_dataset():
url = 'http://deeplearning.net/data/mnist/mnist.pkl.gz'
filename = 'mnist.pkl.gz'
if not os.path.exists(filename):
print("Downloading MNIST dataset...")
urlretrieve(url, filename)
with gzip.open(filename, 'rb') as f:
data = pickle.load(f)
X_train, y_train = data[0]
X_val, y_val = data[1]
X_test, y_test = data[2]
X_train = X_train.reshape((-1, 1, 28, 28))
X_val = X_val.reshape((-1, 1, 28, 28))
X_test = X_test.reshape((-1, 1, 28, 28))
y_train = y_train.astype(np.uint8)
y_val = y_val.astype(np.uint8)
y_test = y_test.astype(np.uint8)
return X_train, y_train, X_val, y_val, X_test, y_test

正如你看到的，我們正在下載處理過的MNIST數據集，接著把它拆分為三個不同的數據集，分別是：訓練集、驗證集和測試集。然后重置圖像內容，為之后的Lasagne輸入層做準備，與此同時，由于GPU/theano數據類型的限制，我們還把numpy的數據類型轉換成了uint8。

隨后，我們準備加載MNIST數據集并檢驗它：
X_train, y_train, X_val, y_val, X_test, y_test = load_dataset()
plt.imshow(X_train[0][0], cmap=cm.binary)

這個代碼將輸出下面的圖像（我用的是IPython Notebook）

一個MNIST數據集的數字實例（該實例是5）

ConvNet體系結構與訓練

現在，定義我們的ConvNet體系結構，然后使用單GPU/CPU來訓練它（我有一個非常廉價的GPU，但它很有用）
net1 = NeuralNet(
layers=[('input', layers.InputLayer),
('conv2d1', layers.Conv2DLayer),
('maxpool1', layers.MaxPool2DLayer),
('conv2d2', layers.Conv2DLayer),
('maxpool2', layers.MaxPool2DLayer),
('dropout1', layers.DropoutLayer),
('dense', layers.DenseLayer),
('dropout2', layers.DropoutLayer),
('output', layers.DenseLayer),
],
# input layer
input_shape=(None, 1, 28, 28),
# layer conv2d1
conv2d1_num_filters=32,
conv2d1_filter_size=(5, 5),
conv2d1_nonlinearity=lasagne.nonlinearities.rectify,
conv2d1_W=lasagne.init.GlorotUniform(),
# layer maxpool1
maxpool1_pool_size=(2, 2),
# layer conv2d2
conv2d2_num_filters=32,
conv2d2_filter_size=(5, 5),
conv2d2_nonlinearity=lasagne.nonlinearities.rectify,
# layer maxpool2
maxpool2_pool_size=(2, 2),
# dropout1
dropout1_p=0.5,
# dense
dense_num_units=256,
dense_nonlinearity=lasagne.nonlinearities.rectify,
# dropout2
dropout2_p=0.5,
# output
output_nonlinearity=lasagne.nonlinearities.softmax,
output_num_units=10,
# optimization method params
update=nesterov_momentum,
update_learning_rate=0.01,
update_momentum=0.9,
max_epochs=10,
verbose=1,
)
# Train the network
nn = net1.fit(X_train, y_train)

如你所視，在layers的參數中，我們定義了一個有層名稱/類型的元組字典，然后定義了這些層的參數。在這里，我們的體系結構使用的是兩個卷積層，兩個池化層，一個全連接層（稠密層，dense layer）和一個輸出層。在一些層之間也會有dropout層，dropout層是一個正則化矩陣，隨機的設置輸入值為零來避免過擬合（見下圖）。

Dropout層效果

調用訓練方法后，nolearn包將會顯示學習過程的狀態，我的機器使用的是低端的的GPU，得到的結果如下：
# Neural Network with 160362 learnable parameters

## Layer information

# name size
--- -------- --------
0 input 1x28x28
1 conv2d1 32x24x24
2 maxpool1 32x12x12
3 conv2d2 32x8x8
4 maxpool2 32x4x4
5 dropout1 32x4x4
6 dense 256
7 dropout2 256
8 output 10

epoch train loss valid loss train/val valid acc dur
------- ------------ ------------ ----------- --------- ---
1 0.85204 0.16707 5.09977 0.95174 33.71s
2 0.27571 0.10732 2.56896 0.96825 33.34s
3 0.20262 0.08567 2.36524 0.97488 33.51s
4 0.16551 0.07695 2.15081 0.97705 33.50s
5 0.14173 0.06803 2.08322 0.98061 34.38s
6 0.12519 0.06067 2.06352 0.98239 34.02s
7 0.11077 0.05532 2.00254 0.98427 33.78s
8 0.10497 0.05771 1.81898 0.98248 34.17s
9 0.09881 0.05159 1.91509 0.98407 33.80s
10 0.09264 0.04958 1.86864 0.98526 33.40s

正如你看到的，最后一次的精度可以達到0.98526，是這10個單元訓練中的一個相當不錯的性能。

預測和混淆矩陣

現在，我們使用這個模型來預測整個測試集：
preds = net1.predict(X_test)

我們還可以繪制一個混淆矩陣來檢查神經網絡的分類性能：
cm = confusion_matrix(y_test, preds)
plt.matshow(cm)
plt.title('Confusion matrix')
plt.colorbar()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()

上面的代碼將繪制下面的混淆矩陣：

混淆矩陣

如你所視，對角線上的分類更密集，表明我們的分類器有一個良好的性能。

過濾器的可視化

我們還可以從第一個卷積層中可視化32個過濾器：
visualize.plot_conv_weights(net1.layers_['conv2d1'])

上面的代碼將繪制下面的過濾器：

第一層的5x5x32過濾器

如你所視，nolearn的plot_conv_weights函數在我們指定的層中繪制出了所有的過濾器。

Theano層的功能和特征提取

現在可以創建theano編譯的函數了，它將前饋輸入數據輸送到結構體系中，甚至是你感興趣的某一層中。接著，我會得到輸出層的函數和輸出層前面的稠密層函數。
dense_layer = layers.get_output(net1.layers_['dense'], deterministic=True)
output_layer = layers.get_output(net1.layers_['output'], deterministic=True)
input_var = net1.layers_['input'].input_var
f_output = theano.function([input_var], output_layer)
f_dense = theano.function([input_var], dense_layer)

如你所視，我們現在有兩個theano函數，分別是f_output和f_dense（用于輸出層和稠密層）。請注意，在這里為了得到這些層，我們使用了一個額外的叫做“deterministic”的參數，這是為了避免dropout層影響我們的前饋操作。

現在，我們可以把實例轉換為輸入格式，然后輸入到theano函數輸出層中：
instance = X_test[0][None, :, :]
%timeit -n 500 f_output(instance)
500 loops, best of 3: 858 μs per loop

如你所視，f_output函數平均需要858μs。我們同樣可以為這個實例繪制輸出層激活值結果：
pred = f_output(instance)
N = pred.shape[1]
plt.bar(range(N), pred.ravel())

上面的代碼將繪制出下面的圖：

?

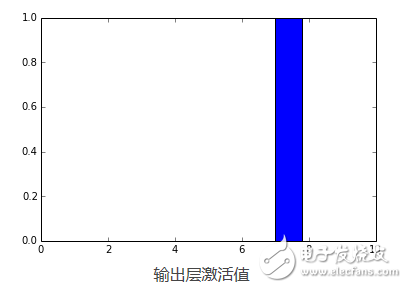
正如你所看到的，數字被認為是7。事實是為任何網絡層創建theano函數都是非常有用的，因為你可以創建一個函數（像我們以前一樣）得到稠密層（輸出層前一個）的激活值，然后你可以使用這些激活值作為特征，并且使用你的神經網絡作為特征提取器而不是分類器。現在，讓我們為稠密層繪制256個激活單元：
pred = f_dense(instance)
N = pred.shape[1]
plt.bar(range(N), pred.ravel())

上面的代碼將繪制下面的圖：

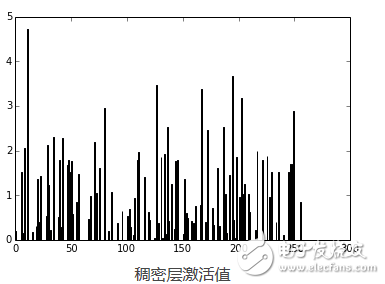
現在，你可以使用輸出的這256個激活值作為線性分類器如Logistic回歸或支持向量機的特征了。

最后，我希望你會喜歡這個教程。

作者簡介：Christian S.Peron，遺傳算法框架Pyevolve（基于Python編寫的）的作者，現任惠普軟件設計師。可通過christian dot perone at gmail dot com 聯系。

關于譯者：?劉帝偉，中南大學軟件學院在讀研究生，關注機器學習、數據挖掘及生物信息領域。