PID=port ID,在STP(生成樹協議)中,若在端口收到的BPDU中BID和path cost相同時,則比較PID來選擇阻塞端口。數字電視復用系統名詞 PID(Packet Identifier) 在數字電視復用系統中它的作用好比一份文件的文件名,我們可以稱它為“標志碼傳輸包” 。工程控制和數學物理方面 PID(比例積分微分)英文全稱為Proportion Integration Differentiation,它是一個數學物理術語。PID由8位端口優先級加端口號組成,端口號占低位,默認端口號優先級128。
ID調節(PID regulating)經典控制理論中控制系統的一種基本調節方式。是具有比例、積分和微分作用的一種線性調節規律。
PID調節(PID regulating)經典控制理論中控制系統的一種基本調節方式。是具有比例、積分和微分作用的一種線性調節規律.PID調節的作用是將給定值r與被控變量的實際量測值y的偏差。-r _y的比例、積分和微分信號綜合成控制量來對被控過程進行控制。這一控制量的表達式為
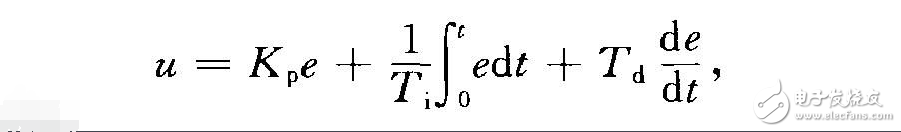
其中K。為比例系數,T;為積分系數,1‘a為微分系數。加大比例系數K。可以減小系統的靜差,但當KP 過大時,會使系統的動態品質變壞,引起被控量振蕩,甚至導致閉環系統不穩定。積分系數T;大說明積分作用弱,反之則說明積分作用強。增大T,將減慢消除靜差的過程,但可以減小超調,提高穩定性。 微分系數Ta增大,則微分作用加強,有助于減少超調,克服振蕩,使系統趨于穩定,加快系統的響應速度,減小調整時間,從而改善系統的動態性能。有眾多的模擬的或數字的PID調節器產品可供選用。用戶只要根據實際應用
pid調節參數整定方法及設置技巧
PID是比例、積分、微分的簡稱,PID控制的難點不是編程,而是控制器的參數整定。參數整定的關鍵是正確地理解各參數的物理意義,PID控制的原理可以用人對爐溫的手動控制來理解。閱讀本文不需要高深的數學知識。
1.比例控制
有經驗的操作人員手動控制電加熱爐的爐溫,可以獲得非常好的控制品質,PID控制與人工控制的控制策略有很多相似的地方。
下面介紹操作人員怎樣用比例控制的思想來手動控制電加熱爐的爐溫。假設用熱電偶檢測爐溫,用數字儀表顯示溫度值。在控制過程中,操作人員用眼睛讀取爐溫,并與爐溫給定值比較,得到溫度的誤差值。然后用手操作電位器,調節加熱的電流,使爐溫保持在給定值附近。
操作人員知道爐溫穩定在給定值時電位器的大致位置(我們將它稱為位置L),并根據當時的溫度誤差值調整控制加熱電流的電位器的轉角。爐溫小于給定值時,誤差為正,在位置L的基礎上順時針增大電位器的轉角,以增大加熱的電流。爐溫大于給定值時,誤差為負,在位置L的基礎上反時針減小電位器的轉角,并令轉角與位置L的差值與誤差成正比。上述控制策略就是比例控制,即PID控制器輸出中的比例部分與誤差成正比。
閉環中存在著各種各樣的延遲作用。例如調節電位器轉角后,到溫度上升到新的轉角對應的穩態值時有較大的時間延遲。由于延遲因素的存在,調節電位器轉角后不能馬上看到調節的效果,因此閉環控制系統調節困難的主要原因是系統中的延遲作用。
比例控制的比例系數如果太小,即調節后的電位器轉角與位置L的差值太小,調節的力度不夠,使系統輸出量變化緩慢,調節所需的總時間過長。比例系數如果過大,即調節后電位器轉角與位置L的差值過大,調節力度太強,將造成調節過頭,甚至使溫度忽高忽低,來回震蕩。
增大比例系數使系統反應靈敏,調節速度加快,并且可以減小穩態誤差。但是比例系數過大會使超調量增大,振蕩次數增加,調節時間加長,動態性能變壞,比例系數太大甚至會使閉環系統不穩定。
單純的比例控制很難保證調節得恰到好處,完全消除誤差。
2.積分控制
PID控制器中的積分對應于圖1中誤差曲線 與坐標軸包圍的面積(圖中的灰色部分)。PID控制程序是周期性執行的,執行的周期稱為采樣周期。計算機的程序用圖1中各矩形面積之和來近似精確的積分,圖中的TS就是采樣周期。
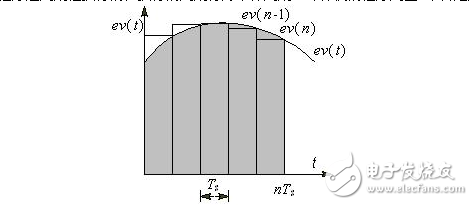
圖1 積分運算示意圖
每次PID運算時,在原來的積分值的基礎上,增加一個與當前的誤差值ev(n)成正比的微小部分。誤差為負值時,積分的增量為負。
手動調節溫度時,積分控制相當于根據當時的誤差值,周期性地微調電位器的角度,每次調節的角度增量值與當時的誤差值成正比。溫度低于設定值時誤差為正,積分項增大,使加熱電流逐漸增大,反之積分項減小。因此只要誤差不為零,控制器的輸出就會因為積分作用而不斷變化。積分調節的“大方向”是正確的,積分項有減小誤差的作用。一直要到系統處于穩定狀態,這時誤差恒為零,比例部分和微分部分均為零,積分部分才不再變化,并且剛好等于穩態時需要的控制器的輸出值,對應于上述溫度控制系統中電位器轉角的位置L。因此積分部分的作用是消除穩態誤差,提高控制精度,積分作用一般是必須的。
PID控制器輸出中的積分部分與誤差的積分成正比。因為積分時間TI在積分項的分母中,TI越小,積分項變化的速度越快,積分作用越強。
3.PI控制
控制器輸出中的積分項與當前的誤差值和過去歷次誤差值的累加值成正比,因此積分作用本身具有嚴重的滯后特性,對系統的穩定性不利。如果積分項的系數設置得不好,其負面作用很難通過積分作用本身迅速地修正。而比例項沒有延遲,只要誤差一出現,比例部分就會立即起作用。因此積分作用很少單獨使用,它一般與比例和微分聯合使用,組成PI或PID控制器。
PI和PID控制器既克服了單純的比例調節有穩態誤差的缺點,又避免了單純的積分調節響應慢、動態性能不好的缺點,因此被廣泛使用。
如果控制器有積分作用(例如采用PI或PID控制),積分能消除階躍輸入的穩態誤差,這時可以將比例系數調得小一些。
如果積分作用太強(即積分時間太小),相當于每次微調電位器的角度值過大,其累積的作用會使系統輸出的動態性能變差,超調量增大,甚至使系統不穩定。積分作用太弱(即積分時間太大),則消除穩態誤差的速度太慢,積分時間的值應取得適中。
4.微分作用
誤差的微分就是誤差的變化速率,誤差變化越快,其微分絕對值越大。誤差增大時,其微分為正;誤差減小時,其微分為負。控制器輸出量的微分部分與誤差的微分成正比,反映了被控量變化的趨勢。
有經驗的操作人員在溫度上升過快,但是尚未達到設定值時,根據溫度變化的趨勢,預感到溫度將會超過設定值,出現超調。于是調節電位器的轉角,提前減小加熱的電流。這相當于士兵射擊遠方的移動目標時,考慮到子彈運動的時間,需要一定的提前量一樣。
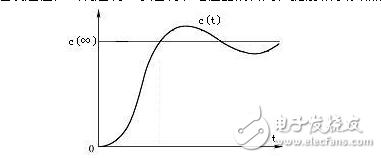
圖2 階躍響應曲線
圖2中的c (∞)為被控量c (t)的穩態值或被控量的期望值,誤差e(t) = c (∞) - c (t)。在圖2中啟動過程的上升階段,當 時,被控量尚未超過其穩態值。但是因為誤差e(t)不斷減小,誤差的微分和控制器輸出的微分部分為負值,減小了控制器的輸出量,相當于提前給出了制動作用,以阻礙被控量的上升,所以可以減少超調量。因此微分控制具有超前和預測的特性,在超調尚未出現之前,就能提前給出控制作用。
閉環控制系統的振蕩甚至不穩定的根本原因在于有較大的滯后因素。因為微分項能預測誤差變化的趨勢,這種“超前”的作用可以抵消滯后因素的影響。適當的微分控制作用可以使超調量減小,增加系統的穩定性。
對于有較大的滯后特性的被控對象,如果PI控制的效果不理想,可以考慮增加微分控制,以改善系統在調節過程中的動態特性。如果將微分時間設置為0,微分部分將不起作用。
微分時間與微分作用的強弱成正比,微分時間越大,微分作用越強。如果微分時間太大,在誤差快速變化時,響應曲線上可能會出現“毛刺”。
微分控制的缺點是對干擾噪聲敏感,使系統抑制干擾的能力降低。為此可在微分部分增加慣性濾波環節。
5.采樣周期
PID控制程序是周期性執行的,執行的周期稱為采樣周期。采樣周期越小,采樣值越能反映模擬量的變化情況。但是太小會增加CPU的運算工作量,相鄰兩次采樣的差值幾乎沒有什么變化,將使PID控制器輸出的微分部分接近為零,所以也不宜將采樣周期取得過小。
應保證在被控量迅速變化時(例如啟動過程中的上升階段),能有足夠多的采樣點數,不致因為采樣點數過少而丟失被采集的模擬量中的重要信息。
6.PID參數的調整方法
在整定PID控制器參數時,可以根據控制器的參數與系統動態性能和穩態性能之間的定性關系,用實驗的方法來調節控制器的參數。有經驗的調試人員一般可以較快地得到較為滿意的調試結果。在調試中最重要的問題是在系統性能不能令人滿意時,知道應該調節哪一個參數,該參數應該增大還是減小。
為了減少需要整定的參數,首先可以采用PI控制器。為了保證系統的安全,在調試開始時應設置比較保守的參數,例如比例系數不要太大,積分時間不要太小,以避免出現系統不穩定或超調量過大的異常情況。給出一個階躍給定信號,根據被控量的輸出波形可以獲得系統性能的信息,例如超調量和調節時間。應根據PID參數與系統性能的關系,反復調節PID的參數。
如果階躍響應的超調量太大,經過多次振蕩才能穩定或者根本不穩定,應減小比例系數、增大積分時間。如果階躍響應沒有超調量,但是被控量上升過于緩慢,過渡過程時間太長,應按相反的方向調整參數。
如果消除誤差的速度較慢,可以適當減小積分時間,增強積分作用。
反復調節比例系數和積分時間,如果超調量仍然較大,可以加入微分控制,微分時間從0逐漸增大,反復調節控制器的比例、積分和微分部分的參數。
總之,PID參數的調試是一個綜合的、各參數互相影響的過程,實際調試過程中的多次嘗試是非常重要的,也是必須的。
7.實驗驗證
實驗使用S7-300 PLC的PID控制功能塊FB 41,被控對象由兩個串聯的慣性環節組成,其時間常數分別為2s和5s,比例系數為3.0。用人機界面的趨勢圖顯示給定曲線和閉環輸出量的響應曲線。
本日志的內容摘自作者在《自動化應用》雜志2010年第5期發表的《PID參數的意義與整定方法》(見附件),該論文給出的實驗結果驗證了本文提出的PID控制器參數的整定方法。
作者將在適當的時候發布用純軟件仿真學習PID參數整定方法的STEP 7項目。
 電子發燒友App
電子發燒友App




















評論