?神經網絡的計算過程

神經網絡結構如下圖所示，最左邊的是輸入層，最右邊的是輸出層，中間是多個隱含層，隱含層和輸出層的每個神經節點，都是由上一層節點乘以其權重累加得到，標上“+1”的圓圈為截距項b，對輸入層外每個節點：Y=w0*x0+w1*x1+…+wn*xn+b，由此我們可以知道神經網絡相當于一個多層邏輯回歸的結構。

?

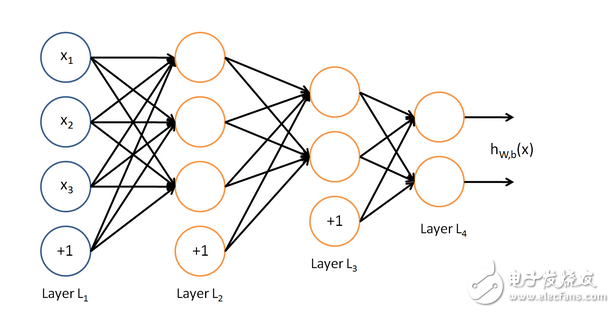
算法計算過程：輸入層開始，從左往右計算，逐層往前直到輸出層產生結果。如果結果值和目標值有差距，再從右往左算，逐層向后計算每個節點的誤差，并且調整每個節點的所有權重，反向到達輸入層后，又重新向前計算，重復迭代以上步驟，直到所有權重參數收斂到一個合理值。由于計算機程序求解方程參數和數學求法不一樣，一般是先隨機選取參數，然后不斷調整參數減少誤差直到逼近正確值，所以大部分的機器學習都是在不斷迭代訓練，下面我們從程序上詳細看看該過程實現就清楚了。

神經網絡的算法程序代碼實現

神經網絡的算法程序實現分為初始化、向前計算結果，反向修改權重三個過程。

1. 初始化過程

由于是n層神經網絡，我們用二維數組layer記錄節點值，第一維為層數，第二維為該層節點位置，數組的值為節點值；同樣，節點誤差值layerErr也是相似方式記錄。用三維數組layer_weight記錄各節點權重，第一維為層數，第二維為該層節點位置，第三維為下層節點位置，數組的值為某節點到達下層某節點的權重值，初始值為0-1之間的隨機數。為了優化收斂速度，這里采用動量法權值調整，需要記錄上一次權值調整量，用三維數組layer_weight_delta來記錄，截距項處理：程序里將截距的值設置為1，這樣只需要計算它的權重就可以了，

2. 向前計算結果

采用S函數1/（1+Math.exp（-z））將每個節點的值統一到0-1之間，再逐層向前計算直到輸出層，對于輸出層，實際上是不需要再用S函數的，我們這里將輸出結果視為0到1之間的概率值，所以也采用了S函數，這樣也有利于程序實現的統一性。

3. 反向修改權重

神經網絡如何計算誤差，一般采用平方型誤差函數E，如下：

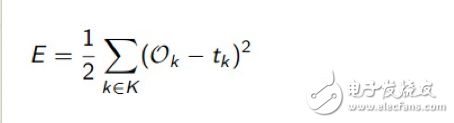
也就是將多個輸出項和對應目標值的誤差的平方累加起來，再除以2。實際上邏輯回歸的誤差函數也是這個，至于為什么要用這個函數來計算誤差，它從數學上的合理性是什么，怎么得來的，這個我建議程序員們不想當數學家的話，先不去深究了，現在我們要做的是如何把這個函數E誤差取它的最小值，需要對其進行求導，如果有些求導數學基礎的話，倒可以嘗試去推導下如何從函數E對權重求導得到下面這個公式的：

?

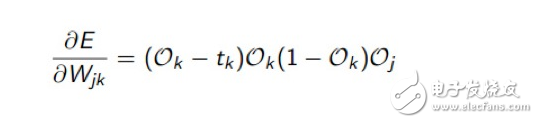
不會推導也沒有關系，我們只需要運用結果公式就可以了，在我們的程序里用layerErr記錄了E對權重求導后的最小化誤差，再根據最小化誤差去調整權重。

注意這里采用動量法調整，將上一次調整的經驗考慮進來，避免陷入局部最小值，下面的k代表迭代次數，mobp為動量項，rate為學習步長：

?

也有很多使用下面的公式，效果上的差別不是太大：

?

為了提升性能，注意程序實現是在一個while里面同時計算誤差和調整權重，先將位置定位到倒數第二層（也就是最后一層隱含層）上，然后逐層反向調整，根據L+1層算好的誤差來調整L層的權重，同時計算好L層的誤差，用于下一次循環到L-1層時計算權重，以此循環下去直到倒數第一層（輸入層）結束。

小結

在整個計算過程中，節點的值是每次計算都在變化的，不需要保存，而權重參數和誤差參數是需要保存的，需要為下一次迭代提供支持，因此，如果我們構思一個分布式的多機并行計算方案，就能理解其他框架中為什么會有一個Parameter Server的概念。

多層神經網絡完整程序實現

下面的實現程序BpDeep.java可以直接拿去使用，也很容易修改為C、C#、Python等其他任何語言實現，因為都是使用的基本語句，沒有用到其他Java庫（除了Random函數）。以下為原創程序，轉載引用時請注明作者和出處。

import java.util.Random;

public class BpDeep{

public double［］［］ layer;//神經網絡各層節點

public double［］［］ layerErr;//神經網絡各節點誤差

public double［］［］［］ layer_weight;//各層節點權重

public double［］［］［］ layer_weight_delta;//各層節點權重動量

public double mobp;//動量系數

public double rate;//學習系數

public BpDeep（int［］ layernum， double rate， double mobp）{

this.mobp = mobp;

this.rate = rate;

layer = new double［layernum.length］［］;

layerErr = new double［layernum.length］［］;

layer_weight = new double［layernum.length］［］［］;

layer_weight_delta = new double［layernum.length］［］［］;

Random random = new Random（）;

for（int l=0;l《layernum.length;l++）{

layer［l］=new double［layernum［l］］;

layerErr［l］=new double［layernum［l］］;

if（l+1《layernum.length）{

layer_weight［l］=new double［layernum［l］+1］［layernum［l+1］］;

layer_weight_delta［l］=new double［layernum［l］+1］［layernum［l+1］］;

for（int j=0;j《layernum［l］+1;j++）

for（int i=0;i《layernum［l+1］;i++）

layer_weight［l］［j］［i］=random.nextDouble（）;//隨機初始化權重

}

}

}

//逐層向前計算輸出

public double［］ computeOut（double［］ in）{

for（int l=1;l《layer.length;l++）{

for（int j=0;j《layer［l］.length;j++）{

double z=layer_weight［l-1］［layer［l-1］.length］［j］;

for（int i=0;i《layer［l-1］.length;i++）{

layer［l-1］［i］=l==1？in［i］：layer［l-1］［i］;

z+=layer_weight［l-1］［i］［j］*layer［l-1］［i］;

}

layer［l］［j］=1/（1+Math.exp（-z））;

}

}

return layer［layer.length-1］;

}

//逐層反向計算誤差并修改權重

public void updateWeight（double［］ tar）{

int l=layer.length-1;

for（int j=0;j《layerErr［l］.length;j++）

layerErr［l］［j］=layer［l］［j］*（1-layer［l］［j］）*（tar［j］-layer［l］［j］）;

while（l--》0）{

for（int j=0;j《layerErr［l］.length;j++）{

double z = 0.0;

for（int i=0;i《layerErr［l+1］.length;i++）{

z=z+l》0？layerErr［l+1］［i］*layer_weight［l］［j］［i］：0;

layer_weight_delta［l］［j］［i］= mobp*layer_weight_delta［l］［j］［i］+rate*layerErr［l+1］［i］*layer［l］［j］;//隱含層動量調整

layer_weight［l］［j］［i］+=layer_weight_delta［l］［j］［i］;//隱含層權重調整

if（j==layerErr［l］.length-1）{

layer_weight_delta［l］［j+1］［i］= mobp*layer_weight_delta［l］［j+1］［i］+rate*layerErr［l+1］［i］;//截距動量調整

layer_weight［l］［j+1］［i］+=layer_weight_delta［l］［j+1］［i］;//截距權重調整

}

}

layerErr［l］［j］=z*layer［l］［j］*（1-layer［l］［j］）;//記錄誤差

}

}

}

public void train（double［］ in， double［］ tar）{

double［］ out = computeOut（in）;

updateWeight（tar）;

}

}

一個運用神經網絡的例子

最后我們找個簡單例子來看看神經網絡神奇的效果。為了方便觀察數據分布，我們選用一個二維坐標的數據，下面共有4個數據，方塊代表數據的類型為1，三角代表數據的類型為0，可以看到屬于方塊類型的數據有（1，2）和（2，1），屬于三角類型的數據有（1，1），（2，2），現在問題是需要在平面上將4個數據分成1和0兩類，并以此來預測新的數據的類型。

?

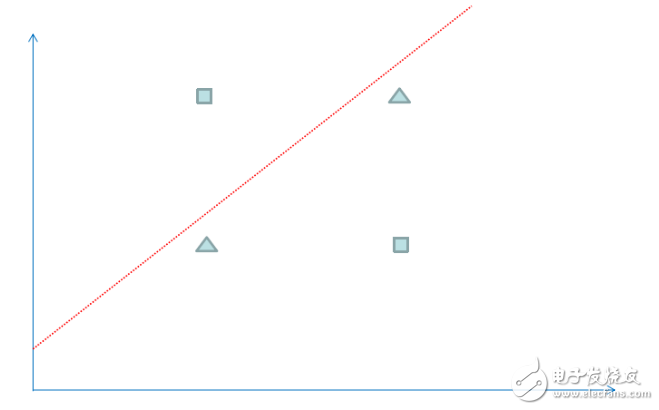
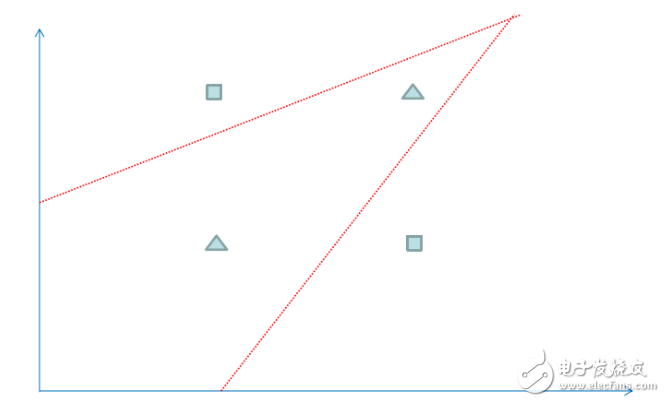
我們可以運用邏輯回歸算法來解決上面的分類問題，但是邏輯回歸得到一個線性的直線做為分界線，可以看到上面的紅線無論怎么擺放，總是有一個樣本被錯誤地劃分到不同類型中，所以對于上面的數據，僅僅一條直線不能很正確地劃分他們的分類，如果我們運用神經網絡算法，可以得到下圖的分類效果，相當于多條直線求并集來劃分空間，這樣準確性更高。

?

下面是這個測試程序BpDeepTest.java的源碼：

import java.util.Arrays;

public class BpDeepTest{

public static void main（String［］ args）{

//初始化神經網絡的基本配置

//第一個參數是一個整型數組，表示神經網絡的層數和每層節點數，比如{3，10，10，10，10，2}表示輸入層是3個節點，輸出層是2個節點，中間有4層隱含層，每層10個節點

//第二個參數是學習步長，第三個參數是動量系數

BpDeep bp = new BpDeep（new int［］{2，10，2}， 0.15， 0.8）;

//設置樣本數據，對應上面的4個二維坐標數據

double［］［］ data = new double［］［］{{1，2}，{2，2}，{1，1}，{2，1}};

//設置目標數據，對應4個坐標數據的分類

double［］［］ target = new double［］［］{{1，0}，{0，1}，{0，1}，{1，0}};

//迭代訓練5000次

for（int n=0;n《5000;n++）

for（int i=0;i《data.length;i++）

bp.train（data［i］， target［i］）;

//根據訓練結果來檢驗樣本數據

for（int j=0;j《data.length;j++）{

double［］ result = bp.computeOut（data［j］）;

System.out.println（Arrays.toString（data［j］）+“：”+Arrays.toString（result））;

}

//根據訓練結果來預測一條新數據的分類

double［］ x = new double［］{3，1};

double［］ result = bp.computeOut（x）;

System.out.println（Arrays.toString（x）+“：”+Arrays.toString（result））;

}

}

小結

以上測試程序顯示神經網絡有很神奇的分類效果，實際上神經網絡有一定優勢，但也不是接近人腦的萬能算法，很多時候它可能會讓我們失望，還需要結合各種場景的數據大量運用去觀察其效果。我們可以把1層隱含層改成n層，并調整每層節點數、迭代次數、學習步長和動量系數，以獲得一個最優化的結果。但是很多時候n層隱含層的效果并不比1層有明顯提升，反而計算更復雜耗時，我們對神經網絡的認識還需要多實踐多體會。