學習過概率的人一定知道貝葉斯定理,在信息領域內有著無與倫比的地位。貝葉斯算法是基于貝葉斯定理的一類算法,主要用來解決分類和回歸問題。
人工智能之機器學習中最為廣泛的兩種分類模型是1)決策樹模型(Decision Tree Model)和2) 樸素貝葉斯模型(Naive Bayesian Model)。
今天我們重點探討一下樸素貝葉斯(NB),注意這里NB不是牛X, 而是Naive Bayesian。 ^_^
樸素貝葉斯是經典的機器學習算法之一,也是為數不多的基于概率論的分類算法。樸素貝葉斯原理簡單,也很容易實現,多用于文本分類、垃圾郵件過濾、情感分析等。
英國數學家托馬斯·貝葉斯(Thomas Bayes)在1763年發表的一篇論文中,首先提出了貝葉斯定理。
貝葉斯定理的應用需要大量的計算,因此歷史上很長一段時間,無法得到廣泛應用。只有計算機誕生以后,它才獲得真正的重視。人們發現,許多統計量是無法事先進行客觀判斷的,而互聯網時代出現的大型數據集,再加上高速運算能力,為驗證這些統計量提供了方便,也為應用貝葉斯定理創造了條件,它的威力正在日益顯現。
概念和定義:
樸素貝葉斯法是基于貝葉斯定理與特征條件獨立假設的分類方法。樸素貝葉斯分類器NBC (NaiveBayes Classifier)發源于古典數學理論,有著堅實的數學基礎,以及穩定的分類效率。樸素貝葉斯分類器(NBC)模型所需估計的參數很少,對缺失數據不太敏感,算法也比較簡單。理論上,NBC模型與其他分類方法相比具有最小的誤差率。但是實際上并非總是如此,這是因為NBC模型假設屬性之間相互獨立,這個假設在實際應用中往往是不成立的,這給NBC模型的正確分類帶來了一定影響。
貝葉斯分類是一系列分類算法總稱,這類算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類。而樸素貝葉斯分類是貝葉斯分類中最簡單,也是常見的一種分類方法。
理論基礎:
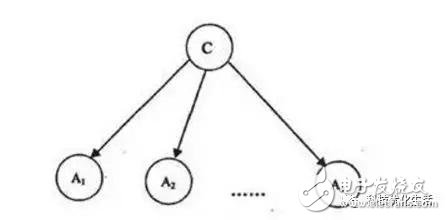
樸素貝葉斯最核心的部分是貝葉斯法則,而貝葉斯法則的基石是條件概率。貝葉斯法則如下:
這里的C表示類別,輸入待判斷數據,式子給出要求解的某一類的概率。
樸素貝葉斯分類器基于一個簡單的假定:給定目標值時屬性之間相互條件獨立。
樸素貝葉斯分類器模型:
Vmap=arg maxP( Vj | a1,a2...an) Vj屬于V集合,其中Vmap是給定一個example,得到的最可能的目標值。其中a1...an是這個example里面的屬性。Vmap目標值,就是后面計算得出的概率最大的一個。所以用max來表示。
貝葉斯公式應用到 P( Vj | a1,a2...an)中。可得到 Vmap= arg max P(a1,a2...an | Vj ) P( Vj ) / P(a1,a2...an)。又因為樸素貝葉斯分類器默認a1...an互相獨立。所以P(a1,a2...an)對于結果沒有用處。可得到Vmap= arg max P(a1,a2...an | Vj ) P( Vj )。
"樸素貝葉斯分類器基于一個簡單的假定:給定目標值時屬性之間相互條件獨立。換言之。該假定說明給定實例的目標值情況下。觀察到聯合的a1,a2...an的概率正好是對每個單獨屬性的概率乘積:P(a1,a2...an | Vj ) =Πi P(ai| Vj )
因此,樸素貝葉斯分類器模型:Vnb=arg max P( Vj ) Π iP ( ai | Vj )
 電子發燒友App
電子發燒友App




































































評論