Part 1: 機(jī)器學(xué)習(xí)的前世今生.
既然說機(jī)器學(xué)習(xí),就從什么機(jī)器學(xué)習(xí)開始,相對(duì)而言,機(jī)器學(xué)習(xí)是一個(gè)比較泛的概念
初看的話,會(huì)覺得機(jī)器學(xué)習(xí)和人工智能,數(shù)據(jù)挖掘講的東西很像,實(shí)際他們之間的關(guān)系可以概括為:
機(jī)器學(xué)習(xí)是人工智能的一個(gè)子方向
機(jī)器學(xué)習(xí)是數(shù)據(jù)挖掘的一種實(shí)現(xiàn)方式
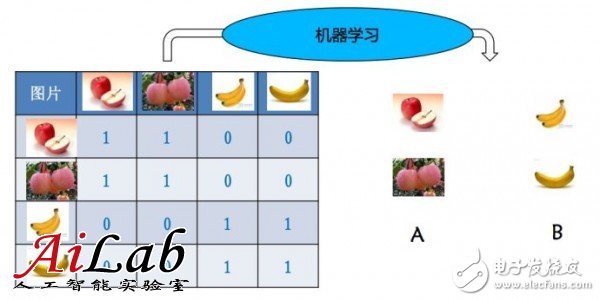
舉個(gè)簡單的例子,給一些蘋果和香蕉,人會(huì)通過特征的判斷做區(qū)分,并且記憶這些特征,下次來了一個(gè)新的蘋果或者香蕉的時(shí)候,就可以判斷是香蕉還是蘋果了
作為任意一個(gè)算法或者說用程序執(zhí)行的數(shù)學(xué)問題,總需要一些輸入,一些輸出
對(duì)于機(jī)器學(xué)習(xí)而言,輸入就是特征所構(gòu)成向量的向量,或者說是一個(gè)矩陣
如果只有一個(gè)特征,輸入就是一個(gè)向量了,當(dāng)然,向量是一個(gè)弱化的矩陣概念,統(tǒng)一稱作矩陣
? 目前機(jī)器學(xué)習(xí)的核心技術(shù)是基于矩陣的優(yōu)化技術(shù)
輸入:矩陣 – 待學(xué)習(xí)的信息
輸出:模型 – 總結(jié)出的規(guī)則
因此,目前主流的機(jī)器學(xué)習(xí)技術(shù)就可以形式化為
?輸入:特征矩陣 X、標(biāo)注向量 y
X 是特征矩陣,不包括“樣本名稱”和“樣本 標(biāo)注”
y 是標(biāo)注向量,即“樣本標(biāo)注”那列
?輸出:模型向量 w
?期望:X·w 盡可能接近 y
多種優(yōu)化算法可以解 w,區(qū)別在于如何定義 “盡可能接近”
舉個(gè)例子來說,要計(jì)算廣告的CTR
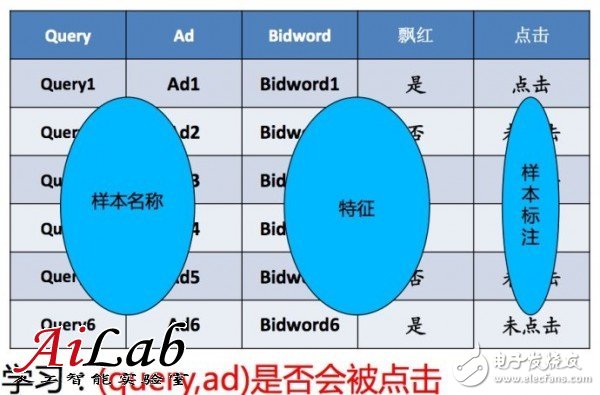
這個(gè)例子中
目標(biāo)是要根據(jù)已知的auc特征,猜測這個(gè)目標(biāo)廣告是否會(huì)被點(diǎn)擊
例子中特征只有兩個(gè),query關(guān)鍵詞和“是否飄紅”,判斷結(jié)果是是否點(diǎn)擊
好了,現(xiàn)在問題和輸入輸出都有了,具體解決這個(gè)問題,就可以選用相關(guān)的算法了
前面定義里面有這么一個(gè)隱含的關(guān)鍵點(diǎn):X w 盡可能接近 y
如何定義這個(gè)“接近”,思路不同,算法就不同
比如對(duì)于LR (Logistic Regression)和SVM(Support Vector Machine)是不同的,作為樣例,可以按照下圖理解
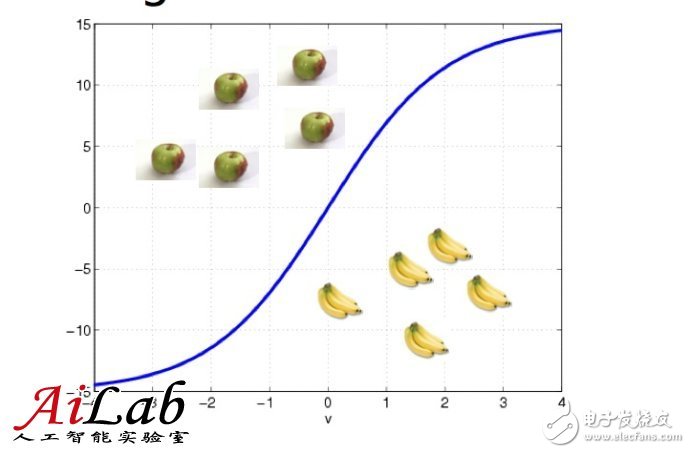
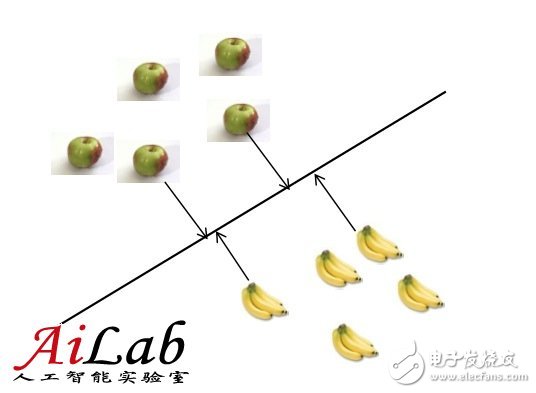
數(shù)學(xué)形式表示,就是
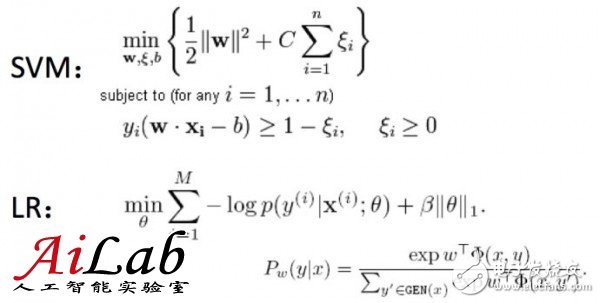
具體算法細(xì)節(jié)不是這里討論的重點(diǎn),在這兩個(gè)算法中,“接近”的定義不同
學(xué)術(shù)的講,就是“優(yōu)化目標(biāo)不同”
無論是否相同,我們都至少可以選一個(gè)優(yōu)化目標(biāo)了
有了優(yōu)化目標(biāo),下面要做的就是如何求解這個(gè)優(yōu)化目標(biāo)了
一般現(xiàn)在用的思路主要是
L-BFGS,CDN,SGD這一些
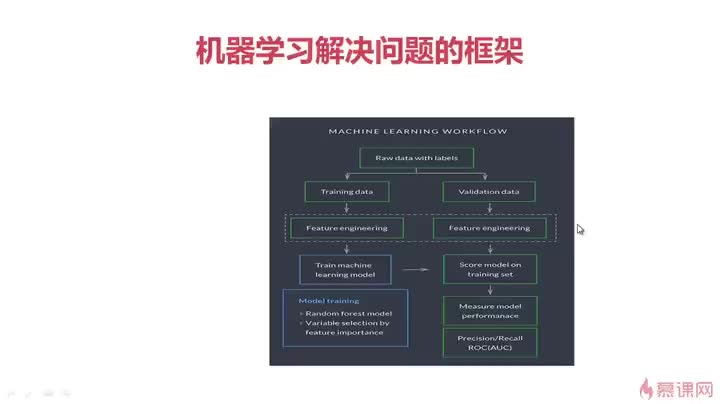
把上面這一些要素放在一起,就有了完整的一個(gè)機(jī)器學(xué)習(xí)問題
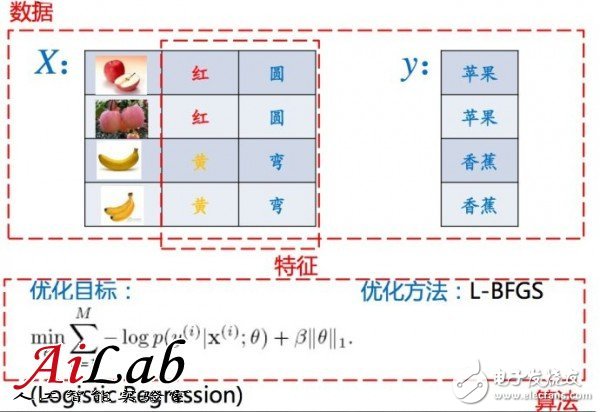
Part 2: 如果你要用機(jī)器學(xué)習(xí)的方法去解決問題
就需要注意三個(gè)方面的優(yōu)化了:
算法,數(shù)據(jù),特征
我們下面分開來說
算法,就是優(yōu)化目標(biāo) + 優(yōu)化算法
從優(yōu)化目標(biāo)的角度,工業(yè)界往往沒有那個(gè)資源或者實(shí)力去研究新的算法,大多是在使用已有算法或者在已有算法的基礎(chǔ)上做擴(kuò)展
從優(yōu)化算法的角度,主要是三點(diǎn):
更小的計(jì)算代價(jià)
更快的收斂
更好的并行
這三點(diǎn)也比較好理解,對(duì)于一個(gè)工程問題,計(jì)算代價(jià)小,機(jī)器就可以做別的事情,更快的收斂,就可以更好的把結(jié)果投入使用,更好的并行,就可以用現(xiàn)有的大數(shù)據(jù)框架解決問題
訓(xùn)練數(shù)據(jù),就是盡可能和實(shí)際同分布的數(shù)據(jù) + 盡可能充分的數(shù)據(jù)
機(jī)器學(xué)習(xí)算法中,由于期望的往往是總的誤差最小,所以很可能講數(shù)據(jù)量小的類目判別錯(cuò)誤
如果樣本數(shù)據(jù)和實(shí)際數(shù)據(jù)分布差異大的話,對(duì)于實(shí)際的算法效果一般都不好
充分的數(shù)據(jù),這個(gè)就好解釋了,數(shù)據(jù)越充分,訓(xùn)練就越充分,就好比考試前做的練習(xí)越多,一般效果越好
特征,就是盡可能包含足夠多的需要識(shí)別對(duì)象的信息
一個(gè)簡單的例子,如果只有一個(gè)特征,對(duì)于水果的判斷往往偏頗,就會(huì)造成下面的結(jié)果
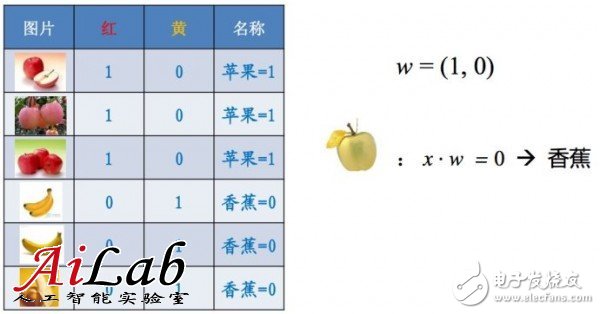
隨著特征的增多,訓(xùn)練就會(huì)準(zhǔn)確
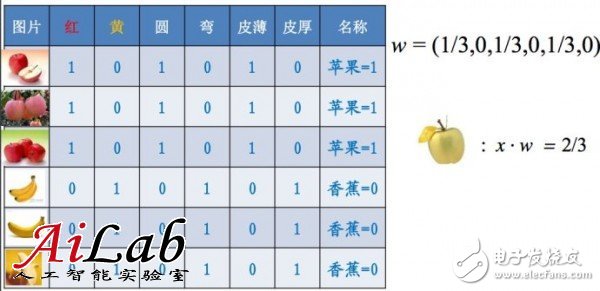
往往對(duì)于一個(gè)工程問題來說,特征是決定最多的方面
一個(gè)算法方面的優(yōu)化,可能只是優(yōu)化了2~3%的效果,但是特征可能就是50~60%了,一個(gè)工程項(xiàng)目七八成的精力往往都是畫在特征選取上的,比如百度CTR預(yù)測,特征數(shù)據(jù)目前就是100億級(jí)別的。
最后來說一點(diǎn)關(guān)于deep learning 的東西
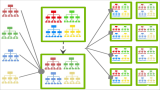
Deep learning和目前的機(jī)器學(xué)習(xí)算法(Shallow Learning)最大的區(qū)別在于特征層數(shù)
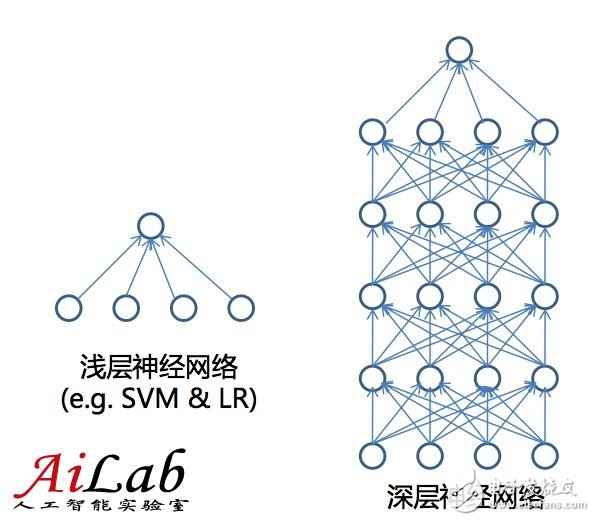
目前的機(jī)器學(xué)習(xí)算法主要是一層的,就是從特征直接推斷是結(jié)果;
而Deep Learning和人類的處理問題的結(jié)果更接近,是由特征推斷出一些中間層的結(jié)果,進(jìn)而推斷出最終結(jié)果的;
比如視覺是由一些點(diǎn),進(jìn)而判斷出一些邊,進(jìn)而判斷出一些形狀,然后才是整體的物體的。
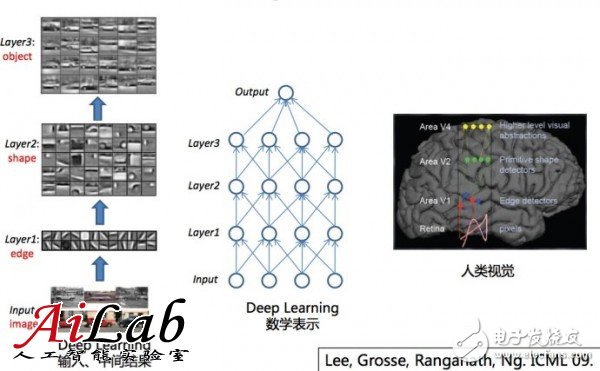
之前大量使用Shallow learning 主要是因?yàn)?Shallow Learning有很好的數(shù)學(xué)特征
解空間是凸函數(shù)
凸函數(shù)有大量的求解方法
凸函數(shù)優(yōu)化可以參考
**Convex Optimization
**
**~boyd/cvxbook/
而Deep Learning則容易找到局部最優(yōu)解,而非全局最優(yōu)解

Deep Learning解法可以參考
G. Hinton et al., A Fast Learning Algorithm for Deep Belief Nets. Neural Computation, 2006.
也可以看Andrew NG最近的課程
這里有最新的中文翻譯http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
 電子發(fā)燒友App
電子發(fā)燒友App













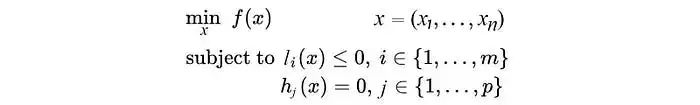











評(píng)論