資料介紹
描述
想象一下擲硬幣九次,連續(xù)九次得到“正面”。第 10 次擲出“反面”的概率是多少?
如果您回答“90%”,那么請(qǐng)繼續(xù)閱讀,當(dāng)然歡迎您稍微回顧一下統(tǒng)計(jì)數(shù)據(jù)。
If, on the other hand, you are among those elected who answer (correctly) "50%", then you already know the difference between dependent and independent events. 正如在統(tǒng)計(jì)領(lǐng)域中所重復(fù)的那樣,一枚硬幣對(duì)其過去沒有記憶,每次拋硬幣正面朝上的概率等于反面朝上的概率。雖然之前的系列看到連續(xù)釋放了 99 個(gè)“反面”,但每次我們將硬幣拋向空中,與概率相關(guān)的數(shù)字都會(huì)重置,我們從頭開始。
顯然,對(duì)于那些像普通人一樣習(xí)慣于在所有感官知覺中尋找模式的人來說,這種行為至少是違反直覺的。我們面臨著一個(gè)通常的、非常古老的故事,它把我們看作是演員,通過試圖識(shí)別每一個(gè)現(xiàn)實(shí)表現(xiàn)背后的根本原因來尋求改善我們的狀態(tài)。
從硬幣到骰子
如果我們正好有 50% 的機(jī)會(huì)看到硬幣正面朝上或反面朝上(忽略硬幣站在邊緣的那些罕見的例外情況),骰子的每一面出現(xiàn)的幾率是多少?很簡(jiǎn)單:每次滾動(dòng),每張臉都有六分之一的機(jī)會(huì)出現(xiàn)。所以,大約 16.67%。
換句話說,從 1 到 6 的每個(gè)值都具有完全相同的退出概率(除非你已經(jīng)密封了骰子……)。
當(dāng)我們?cè)黾訑S骰子的數(shù)量時(shí),事情會(huì)變得更有趣:無論如何,實(shí)際上用兩個(gè)骰子獲得值 1 是不可能的(顯然……)。在下表中,我們可以看到有多少種不同的方法可以獲得每個(gè)值作為結(jié)果。
?
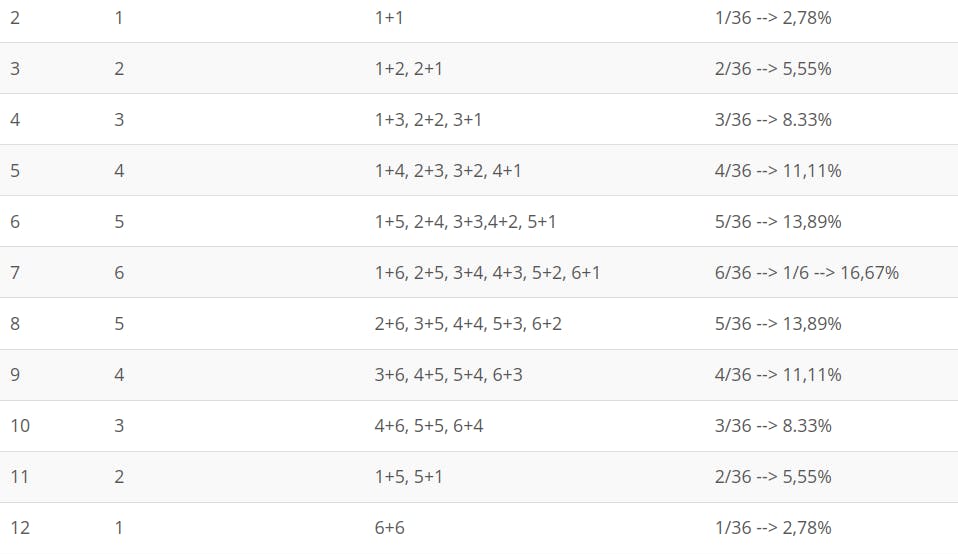
用一點(diǎn)組合數(shù)學(xué)(但也只是常識(shí))很容易認(rèn)識(shí)到每個(gè)數(shù)字的輸出可能性不再相同,因?yàn)槟承┲悼梢砸詭追N不同的方式組合。如果我們看一下表格,我們會(huì)發(fā)現(xiàn)每次投擲都有 36 種不同的可能組合。值 2 和值 12 在每次擲骰時(shí)都有 36 分之一的機(jī)會(huì)出現(xiàn),值 3 和值 11 在每次擲骰時(shí)各有 2 次退出的概率,依此類推。換句話說,對(duì)于單個(gè)骰子,每個(gè)數(shù)字出來的概率不再相同,特別是兩個(gè)骰子出現(xiàn)2或12的概率等于出一個(gè)正數(shù)在輪盤賭中。(如果我們暫時(shí)不考慮零,則為 1/36 或 2.78%)。
讓我們?cè)黾訌?fù)雜性。
如果我們使用兩個(gè)以上的骰子會(huì)發(fā)生什么?每個(gè)版本的幾率是多少?他們會(huì)保持增長的明顯線性,還是會(huì)創(chuàng)造出奇怪的曲線?我們可以手動(dòng)計(jì)算這些值,但隨著計(jì)算量的增加,我們會(huì)冒犯錯(cuò)誤的風(fēng)險(xiǎn)。另一方面,計(jì)算機(jī)會(huì)非常輕松......
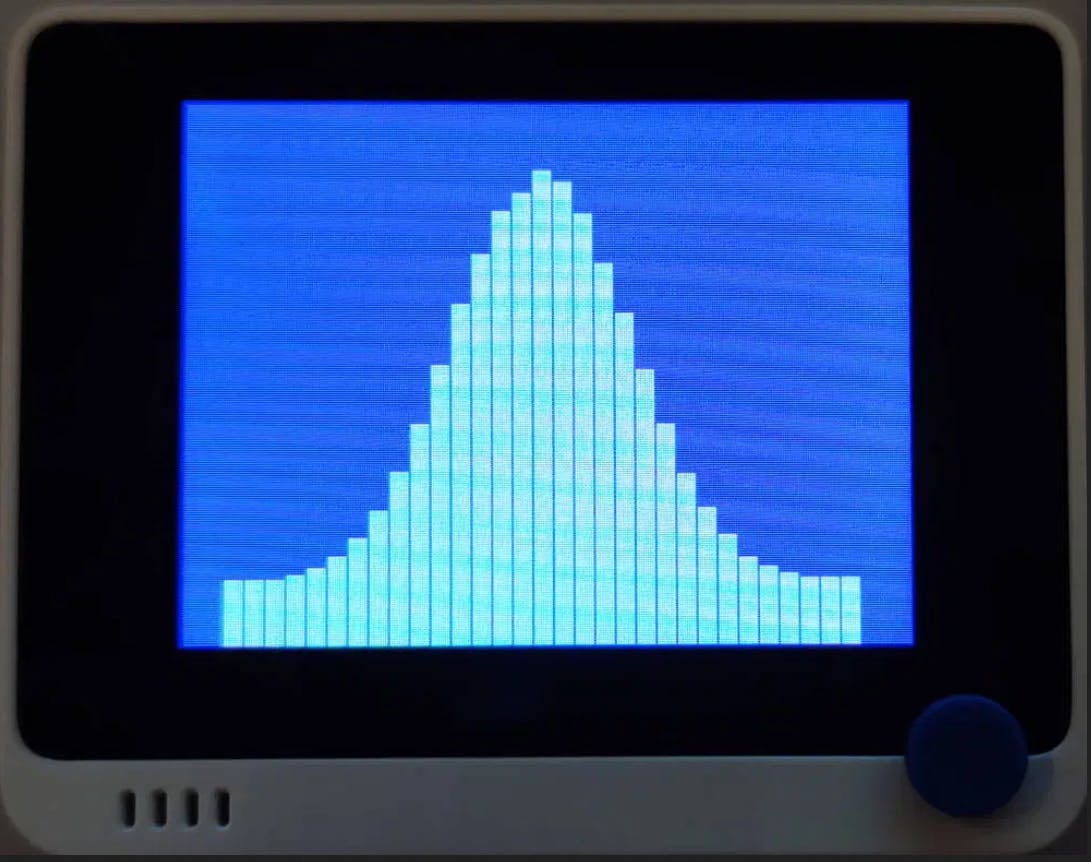
我們有一個(gè)具有特殊計(jì)算能力的小板,即Seeeduino Wio 終端。這是一個(gè) Arduino 類固醇,配備SAMD51系統(tǒng)和ARM Cortex M4 處理器。只需編寫一個(gè)簡(jiǎn)單的程序,使用 random() 函數(shù)模擬擲 6 個(gè)骰子,將每個(gè)組合的輸出值累加并計(jì)算總輸出的百分比。
?
為了使程序更有趣,我們將在表格中添加每個(gè)組合的輸出數(shù)量顯示。
在程序結(jié)束時(shí),只需單擊藍(lán)色按鈕即可獲得為每個(gè)組合計(jì)算的概率值列表。
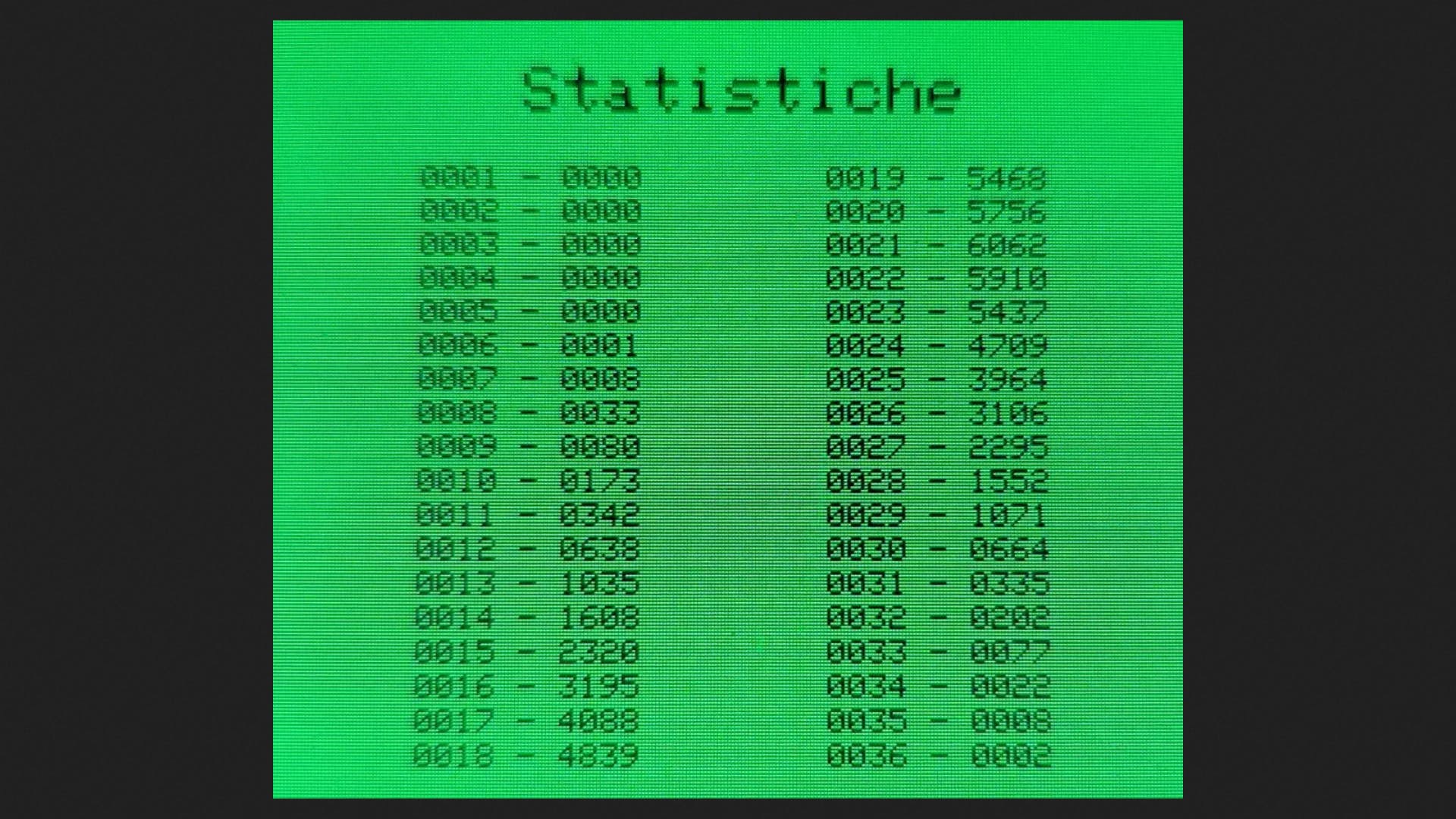
該程序可在GitHub和附件部分獲取。
如果您需要澄清,請(qǐng)隨時(shí)與我聯(lián)系。
?
- Seeed Wio終端開源分享
- Lyapunov分形與Seeeduino Wio終端開源
- 如何使用Seeeduino XIAO-LED閃爍
- 使用Wio Terminal和Tensorflow Lite創(chuàng)建智能氣象站
- 用于FPGA的賭場(chǎng)擲骰子游戲
- 使用Seeeduino Xiao從汽車中獲取數(shù)據(jù)
- 簡(jiǎn)單的擲骰子草圖開源分享
- 在Wio終端上顯示精確的分貝計(jì) 0次下載
- Seeeduino v4.2評(píng)測(cè)
- 使用Wio終端擴(kuò)展Arduboy
- Seeeduino XIAO氣象站使用擴(kuò)展板
- 使用Wio終端讀取OBD2
- RH1016骰子規(guī)格
- Seeeduino XIAO擴(kuò)展板的電路原理圖 45次下載
- 電骰子電路設(shè)計(jì)論文 101次下載
- CAN總線終端電阻添加要求 4681次閱讀
- 分享一個(gè)棋盤游戲電子骰子電路 2234次閱讀
- 智能交互終端是什么 智能交互終端怎么裝 3399次閱讀
- 三個(gè)簡(jiǎn)單的電子骰子電路分析 5765次閱讀
- 基于AT89C205構(gòu)建的電子骰子的電路圖 2178次閱讀
- 如何利用TinyML實(shí)現(xiàn)語音識(shí)別機(jī)器人車的設(shè)計(jì) 2110次閱讀
- 如何通過藍(lán)牙微控制器控制多功能骰子? 2905次閱讀
- 帶反接保護(hù)的電子骰子電路 3381次閱讀
- 隱馬爾可夫模型描述一個(gè)含有隱含未知參數(shù)的馬爾可夫過程 4417次閱讀
- LED骰子diy教程 4650次閱讀
- 蒙特卡洛模擬方法 9496次閱讀
- 通信終端設(shè)備有哪些_通信終端設(shè)備盤點(diǎn) 2.9w次閱讀
- 什么是模擬電路_模擬電路為什么叫模擬 2.5w次閱讀
- 什么是超級(jí)終端_超級(jí)終端是干什么用的 2.3w次閱讀
- 驅(qū)動(dòng)電子骰子至少需要幾個(gè)I/O口? 3962次閱讀
下載排行
本周
- 1山景DSP芯片AP8248A2數(shù)據(jù)手冊(cè)
- 1.06 MB | 532次下載 | 免費(fèi)
- 2RK3399完整板原理圖(支持平板,盒子VR)
- 3.28 MB | 339次下載 | 免費(fèi)
- 3TC358743XBG評(píng)估板參考手冊(cè)
- 1.36 MB | 330次下載 | 免費(fèi)
- 4DFM軟件使用教程
- 0.84 MB | 295次下載 | 免費(fèi)
- 5元宇宙深度解析—未來的未來-風(fēng)口還是泡沫
- 6.40 MB | 227次下載 | 免費(fèi)
- 6迪文DGUS開發(fā)指南
- 31.67 MB | 194次下載 | 免費(fèi)
- 7元宇宙底層硬件系列報(bào)告
- 13.42 MB | 182次下載 | 免費(fèi)
- 8FP5207XR-G1中文應(yīng)用手冊(cè)
- 1.09 MB | 178次下載 | 免費(fèi)
本月
- 1OrCAD10.5下載OrCAD10.5中文版軟件
- 0.00 MB | 234315次下載 | 免費(fèi)
- 2555集成電路應(yīng)用800例(新編版)
- 0.00 MB | 33566次下載 | 免費(fèi)
- 3接口電路圖大全
- 未知 | 30323次下載 | 免費(fèi)
- 4開關(guān)電源設(shè)計(jì)實(shí)例指南
- 未知 | 21549次下載 | 免費(fèi)
- 5電氣工程師手冊(cè)免費(fèi)下載(新編第二版pdf電子書)
- 0.00 MB | 15349次下載 | 免費(fèi)
- 6數(shù)字電路基礎(chǔ)pdf(下載)
- 未知 | 13750次下載 | 免費(fèi)
- 7電子制作實(shí)例集錦 下載
- 未知 | 8113次下載 | 免費(fèi)
- 8《LED驅(qū)動(dòng)電路設(shè)計(jì)》 溫德爾著
- 0.00 MB | 6656次下載 | 免費(fèi)
總榜
- 1matlab軟件下載入口
- 未知 | 935054次下載 | 免費(fèi)
- 2protel99se軟件下載(可英文版轉(zhuǎn)中文版)
- 78.1 MB | 537798次下載 | 免費(fèi)
- 3MATLAB 7.1 下載 (含軟件介紹)
- 未知 | 420027次下載 | 免費(fèi)
- 4OrCAD10.5下載OrCAD10.5中文版軟件
- 0.00 MB | 234315次下載 | 免費(fèi)
- 5Altium DXP2002下載入口
- 未知 | 233046次下載 | 免費(fèi)
- 6電路仿真軟件multisim 10.0免費(fèi)下載
- 340992 | 191187次下載 | 免費(fèi)
- 7十天學(xué)會(huì)AVR單片機(jī)與C語言視頻教程 下載
- 158M | 183279次下載 | 免費(fèi)
- 8proe5.0野火版下載(中文版免費(fèi)下載)
- 未知 | 138040次下載 | 免費(fèi)
 電子發(fā)燒友App
電子發(fā)燒友App

















 創(chuàng)作
創(chuàng)作 發(fā)文章
發(fā)文章 發(fā)帖
發(fā)帖  提問
提問  發(fā)資料
發(fā)資料 發(fā)視頻
發(fā)視頻 上傳資料賺積分
上傳資料賺積分









評(píng)論