寫在之前
支持向量機(SVM),一個神秘而眾知的名字,在其出來就受到了莫大的追捧,號稱最優秀的分類算法之一,以其簡單的理論構造了復雜的算法,又以其簡單的用法實現了復雜的問題,不得不說確實完美。
本系列旨在以基礎化的過程,實例化的形式一探SVM的究竟。曾經也只用過集成化的SVM軟件包,效果確實好。因為眾人皆說原理復雜就對其原理卻沒怎么研究,最近經過一段時間的研究感覺其原理還是可以理解,這里希望以一個從懵懂到略微熟知的角度記錄一下學習的過程。其實網絡上講SVM算法的多不勝數,博客中也有許多大師級博主的文章,寫的也很簡單明了,可是在看過之和總是感覺像差點什么,當然對于那些基礎好的可能一看就懂了,然而對于像我們這些薄基礎的一遍下來也能馬馬虎虎懂,過一兩天后又忘了公式怎么來的了。比如說在研究SVM之前,你是否聽說過拉格朗日乘子法?你是否知道什么是對偶問題?你是否了解它們是怎么解決問題的?Ok這些不知道的話,更別說什么是KKT條件了,哈哈,有沒有說到你的心聲,不用怕,學學就會了。話說像拉格朗日乘子法,在大學里面學數學的話,不應該沒學過,然你學會了嗎?你知道是干什么的嗎?如果那個時候就會了,那你潛質相當高了。作為一個過來的人,將以簡單實例化形式記錄自己的學習過程,力圖幫助新手級學習者少走彎路。
一、關于拉格朗日乘子法和KKT條件
1)關于拉格朗日乘子法
首先來了解拉格朗日乘子法,那么為什么需要拉格朗日乘子法?記住,有拉格朗日乘子法的地方,必然是一個組合優化問題。那么帶約束的優化問題很好說,就比如說下面這個:
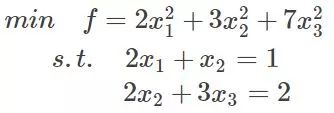
這是一個帶等式約束的優化問題,有目標值,有約束條件。那么想想假設沒有約束條件這個問題是怎么求解的呢?是不是直接f對各個x求導等于0,,解x就可以了,可以看到沒有約束的話,求導為0,那么各個x均為0吧,這樣f=0了,最小。但是x都為0不滿足約束條件呀,那么問題就來了。這里在說一點的是,為什么上面說求導為0就可以呢?理論上多數問題是可以的,但是有的問題不可以。如果求導為0一定可以的話,那么f一定是個凸優化問題,什么是凸的呢?像下面這個左圖:
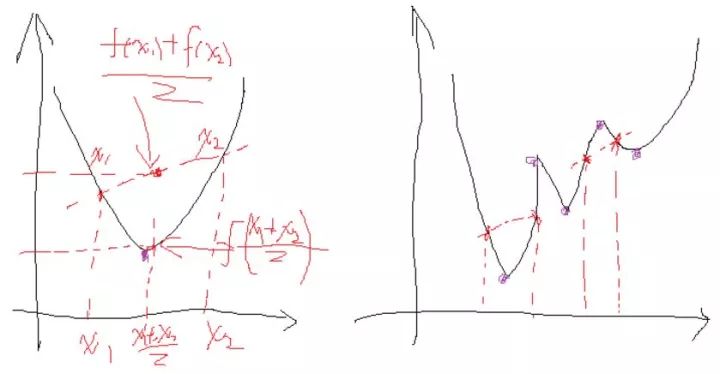
凸的就是開口朝一個方向(向上或向下)。更準確的數學關系就是:
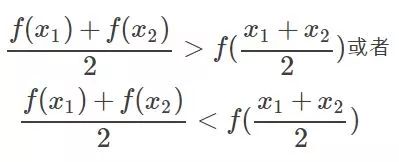
注意的是這個條件是對函數的任意x取值。如果滿足第一個就是開口向上的凸,第二個是開口向下的凸。可以看到對于凸問題,你去求導的話,是不是只有一個極點,那么他就是最優點,很合理。類似的看看上圖右邊這個圖,很明顯這個條件對任意的x取值不滿足,有時滿足第一個關系,有時滿足第二個關系,對應上面的兩處取法就是,所以這種問題就不行,再看看你去對它求導,會得到好幾個極點。然而從圖上可以看到,只有其中一個極點是最優解,其他的是局部最優解,那么當真實問題的時候你選擇那個?說了半天要說啥呢,就是拉格朗日法是一定適合于凸問題的,不一定適合于其他問題,還好我們最終的問題是凸問題。
回頭再來看看有約束的問題,既然有了約束不能直接求導,那么如果把約束去掉不就可以了嗎?怎么去掉呢?這才需要拉格朗日方法。既然是等式約束,那么我們把這個約束乘一個系數加到目標函數中去,這樣就相當于既考慮了原目標函數,也考慮了約束條件,比如上面那個函數,加進去就變為: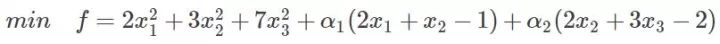
這里可以看到與相乘的部分都為0,所以的取值為全體實數。現在這個優化目標函數就沒有約束條件了吧,既然如此,求法就簡單了,分別對x求導等于0,如下:
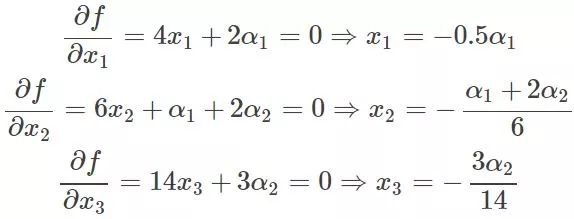
把它在帶到約束條件中去,可以看到,2個變量兩個等式,可以求解,最終可以得到,這樣再帶回去求x就可以了。那么一個帶等式約束的優化問題就通過拉格朗日乘子法完美的解決了。那么更高一層的,帶有不等式的約束問題怎么辦?那么就需要用更一般化的拉格朗日乘子法即KKT條件來解決這種問題了。
2)關于KKT條件
繼續討論關于帶等式以及不等式的約束條件的凸函數優化。任何原始問題約束條件無非最多3種,等式約束,大于號約束,小于號約束,而這三種最終通過將約束方程化簡化為兩類:約束方程等于0和約束方程小于0。再舉個簡單的方程為例,假設原始約束條件為下列所示:
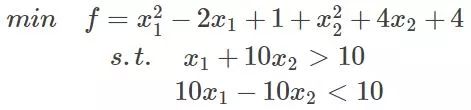
那么把約束條件變個樣子:
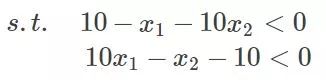
為什么都變成等號與小于號,方便后面的,反正式子的關系沒有發生任何變化就行了。
現在將約束拿到目標函數中去就變成:
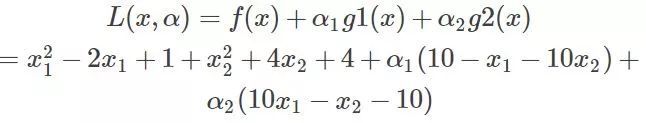
那么KKT條件的定理是什么呢?就是如果一個優化問題在轉變完后變成
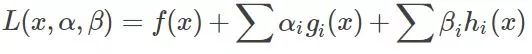
其中g是不等式約束,h是等式約束(像上面那個只有不等式約束,也可能有等式約束)。那么KKT條件就是函數的最優值必定滿足下面條件:
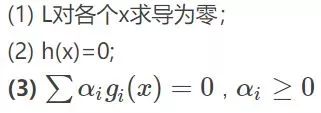
這三個式子前兩個好理解,重點是第三個式子不好理解,因為我們知道在約束條件變完后,所有的g(x)<=0,且,然后求和還要為0,無非就是告訴你,要么某個不等式,要么其對應的。那么為什么KKT的條件是這樣的呢?
假設有一個目標函數,以及它的約束條件,形象的畫出來就如下:
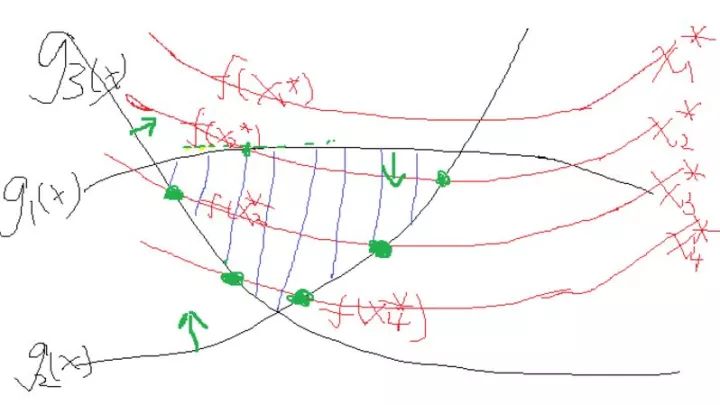
假設就這么幾個吧,最終約束是把自變量約束在一定范圍,而函數是在這個范圍內尋找最優解。函數開始也不知道該取哪一個值是吧,那就隨便取一個,假設某一次取得自變量集合為x1,發現一看,不滿足約束,然后再換呀換,換到了x2,發現可以了,但是這個時候函數值不是最優的,并且x2使得g1(x)與g2(x)等于0了,而g3(x)還是小于0。
這個時候,我們發現在x2的基礎上再尋找一組更優解要靠誰呢?當然是要靠約束條件g1(x)與g2(x),因為他們等于0了,很極限呀,一不小心,走錯了就不滿足它們兩了,這個時候我們會選擇g1(x)與g2(x)的梯度方向往下走,這樣才能最大程度的拜托g1(x)與g2(x)=0的命運,使得他們滿足小于0的約束條件對不對。至于這個時候需不需要管g3(x)呢?正常來說管不管都可以,如果管了,也取g3在x2處的梯度的話,因為g3已經滿足了小于0的條件,這個時候在取在x2處的梯度,你能保證它是往好的變了還是往差的變了?答案是都有可能。運氣好,往好的變了,可以更快得到結果,運氣不好,往差的變了,反而適得其反。
那么如果不管呢?因為g1(x)與g2(x)已經在邊緣了,所以取它的梯度是一定會讓目標函數變好的。綜合來看,這個時候我們就不選g3。那么再往下走,假設到了自變量優化到了x3,這個時候發現g2(x)與g3(x)等于0,也就是走到邊了,而g1(x)小于0,可變化的空間綽綽有余,那么這個時候舉要取g2(x)與g3(x)的梯度方向作為變化的方向,而不用管g1(x)。那么一直這樣走呀走,最終找到最優解。可以看到的是,上述如果g1(x)、g2(x)=0的話,我們是需要優化它的,又因為他們本身的條件是小于0的,所以最終的公式推導上表明,是要乘以一個正系數作為他們梯度增長的倍數,而那些不需要管的g(x)為了統一表示,這個時候可以將這個系數設置為0,那么這一項在這一次的優化中就沒有了。那么把這兩種綜合起來就可以表示為
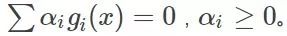
也即是某次的g(x)在為最優解起作用,那么它的系數值(可以)不為0。如果某次g(x)沒有為下一次的最優解x的獲得起到作用,那么它的系數就必須為0,這就是這個公式的含義。
比如上面例子的目標值與約束:
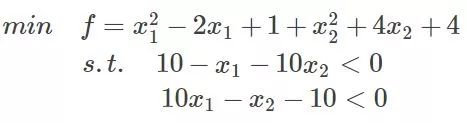
將約束提到函數中有:
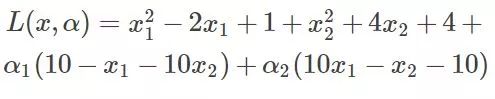
此時分別對x1、x2求導數:
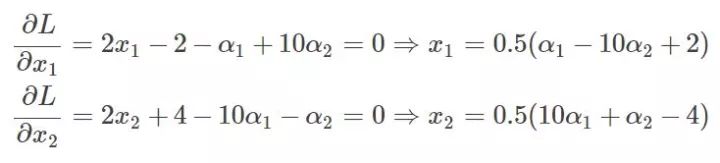
而我們還有一個條件就是,那么也就是:
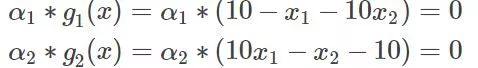
這樣我們就去討論下,要么g=0,要么,這里兩個g兩個,這樣我們就需要討論四種情況,可能你會說,這是約束條件少的情況,那么如果有10個約束條件,這樣就有10個g和10個,你去給我討論?多少種組合,不知道,但是換個思路,我們非得去10個一起去討論?機智的學者想到一種方法,考慮到這個條件,那么我兩個兩個討論不就可以了,比如現在我就討論7,8,讓其他的不變,為什么選或者至少選兩個討論呢,因為這個式子求和為0,改變一個顯然是不行的,那就改變兩個,你增我就減,這樣和可以為0。再問為什么不討論3個呢?也可以,這不是麻煩嘛,一個俗語怎么說來著,三個和尚沒水喝,假設你改變了一個,另外兩個你說誰去減或者加使得和為0,還是兩個都變化一點呢?不好說吧,自然界都是成雙成對的才和諧,沒有成三成四的(有的話也少)。
這里順便提一下后面會介紹到的內容,就是實現SVM算法的SMO方法,在哪里,會有很多,那么人們怎么解決的呢,就是隨便選擇兩個去變化,看看結果好的話,就接受,不好的話就舍棄在選擇兩個,如此反復,后面介紹。

可以看到像這種簡單的討論完以后就可以得到解了。
x1=110/101=1.08;x2=90/101=0.89,那么它得到結果對不對呢?這里因為函數簡單,可以在matlab下畫出來,同時約束條件也可以畫出來,那么原問題以及它的約束面畫出來就如下所示:
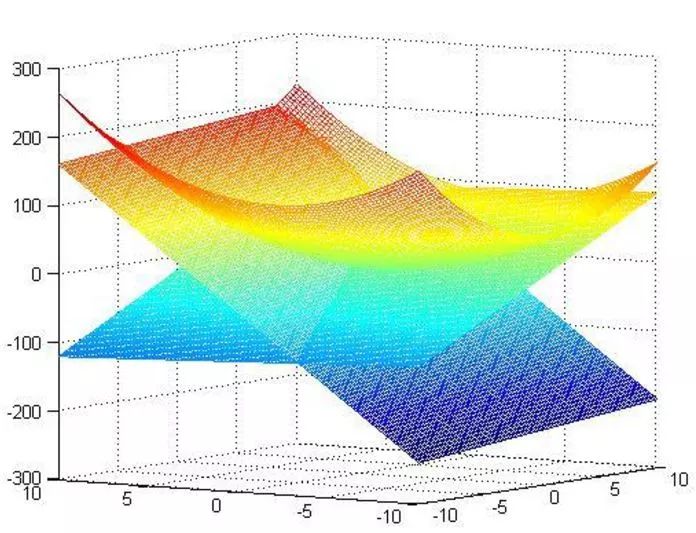
這是截取下來的符合約束要求的目標面
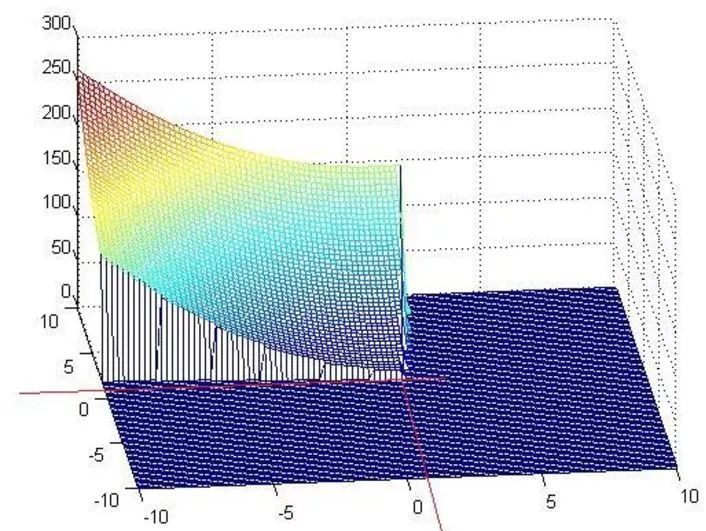
可以看到最優解確實就是上面我們求的那個解。既然簡單的問題可以這樣解,那么復雜一點的只需要簡單化,照樣可以解,至此KKT條件解這類約束性問題就是這樣,它對后續的SVM求解最優解至關重要。
二、SVM的理論基礎
上節我們探討了關于拉格朗日乘子和KKT條件,這為后面SVM求解奠定基礎,本節希望通俗的細說一下原理部分。
一個簡單的二分類問題如下圖:
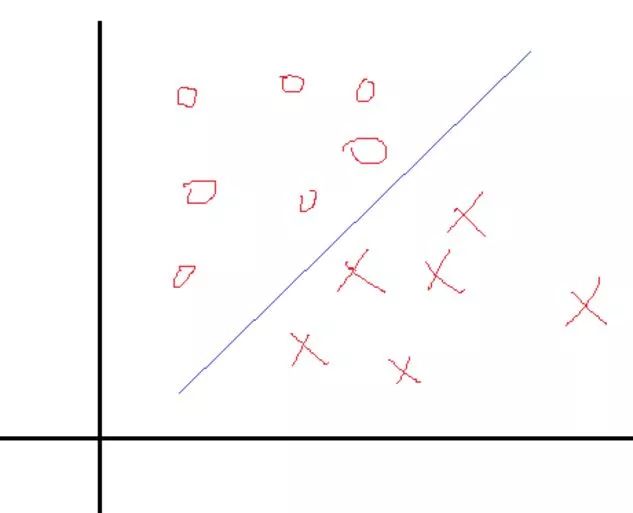
我們希望找到一個決策面使得兩類分開,這個決策面一般表示就是W'X+b=0,現在的問題是找到對應的W和b使得分割最好,知道logistic分類機器學習之logistic回歸與分類的可能知道,這里的問題和那里的一樣,也是找權值。在那里,我們是根據每一個樣本的輸出值與目標值得誤差不斷的調整權值W和b來求得最終的解的。當然這種求解最優的方式只是其中的一種方式。那么SVM的求優方式是怎樣的呢?
這里我們把問題反過來看,假設我們知道了結果,就是上面這樣的分類線對應的權值W和b。那么我們會看到,在這兩個類里面,是不是總能找到離這個線最近的點,向下面這樣:
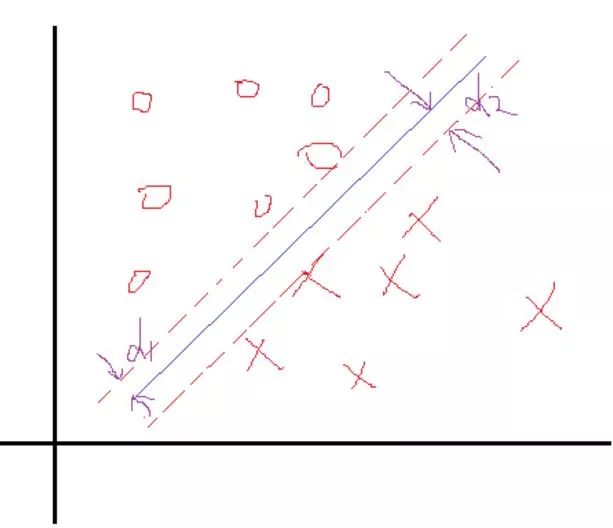
然后定義一下離這個線最近的點到這個分界面(線)的距離分別為d1,d2。那么SVM找最優權值的策略就是,先找到最邊上的點,再找到這兩個距離之和D,然后求解D的**最大值**,想想如果按照這個策略是不是可以實現最優分類,是的。好了,還是假設找到了這樣一個分界面W'X+b=0,那么做離它最近的兩類點且平行于分類面,如上面的虛線所示。
好了再假設我們有這兩個虛線,那么真實的分界面我們認為正好是這兩個分界面的中間線,這樣d1就等于d2了。因為真實的分界面為W'X+b=0,那么就把兩個虛線分別設置為W'X+b=1和W'X+b=-1,可以看到虛線相對于真實面只是上下移動了1個單位距離,可能會說你怎么知道正好是一個距離?確實不知道,就假設上下是k個距離吧,那么假設上虛線現在為W'X+b=k,兩邊同時除k可以吧,這樣上虛線還是可以變成W'X+b=1,同理下虛線也可以這樣,然后他們的中線就是W1'X+b1=0吧,可以看到從k到1,權值無非從w變化到w1,b變到b1,我在讓w=w1,b=b1,不是又回到了起點嗎,也就是說,這個中間無非是一個倍數關系。
所以我們只需要先確定使得上下等于1的距離,再去找這一組權值,這一組權值會自動變化到一定倍數使得距離為1的。
好了再看看D=d1+d2怎么求吧,假設分界面W'X+b=0,再假設X是兩維的,那么分界面再細寫出來就是:W1'X1+W2'X2+b=0。上分界線:W1'X1+W2'X2+b=1,這是什么,兩條一次函數(y=kx+b)的曲線是不是,那么初中就學過兩直線的距離吧,
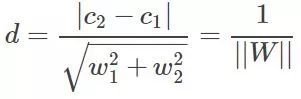
這里W=(w1,w2),是個向量,||W||為向量的距離,那么||W||^2=W'W。下界面同理。這樣
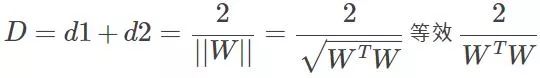
,
要使D最大,就要使分母最小,這樣優化問題就變為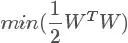 ,乘一個系數0.5沒影響,但是在后面卻有用。
,乘一個系數0.5沒影響,但是在后面卻有用。

注意的是這可不是一個約束條件,而是對所有的每個樣本xi都有一個這樣的約束條件。轉換到這種形式以后是不是很像上節說到的KKT條件下的優化問題了,就是這個。但是有一個問題,我們說上節的KKT是在凸函數下使用的,那么這里的目標函數是不是呢?答案是的,想想W'*W,函數乘出來應該很單一,不能有很多極點,當然也也可以數學證明是的。
好了那樣的話就可以引入拉格朗日乘子法了,優化的目標變為:
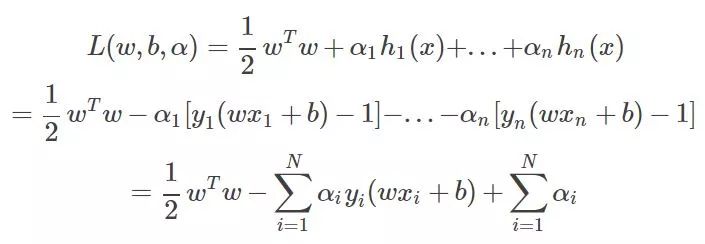
然后要求這個目標函數最優解,求導吧,
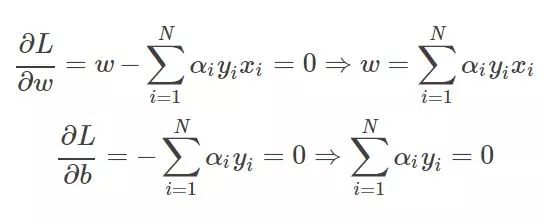
這兩個公式非常重要,簡直是核心公式。
求導得到這個應該很簡單吧,那我問你為什么W'W 對w求導是w呢?如果你知道,那么你很厲害了,反正開始我是一直沒轉過來。其實說起來也很簡單,如果光去看看為什么求導以后,轉置就沒了,不太好想明白,設想一下假設現在是二維樣本點,也就是最終的W=(w1,w2),那么W'W=w1*w1+w2*w2那么對w1求導就是2w1,對w2就是2w2,這樣寫在一起就是對w求導得到(2w1,2w2)=2w了,然后乘前面一個1/2(這也就是為什么要加一個1/2),就變成w了。
好了得到上面的兩個公式,再帶回L中把去w和b消掉,你又可能發現,w確實可以消,因為有等式關系,那b怎么辦?上述對b求導的結果竟然不含有b,上天在開玩笑嗎?其實沒有,雖然沒有b,但是有那個求和為0呀,帶進去你會驚人的發現,b還真的可以消掉,就是因為了那個等式。簡單帶下:
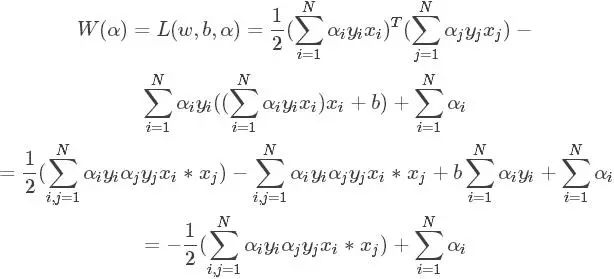
那么求解最最開始的函數的最小值等價到這一步以后就是求解W的最大值了,因為使用了拉格朗日乘子法后,原問題就變為其對偶問題了,最小變成了最大,至于為什么,等到詳細研究過對偶問題再來解釋吧。不了解的,只需要知道求W的極值即可。整理一下,經過這么一圈的轉化,最終的問題為:
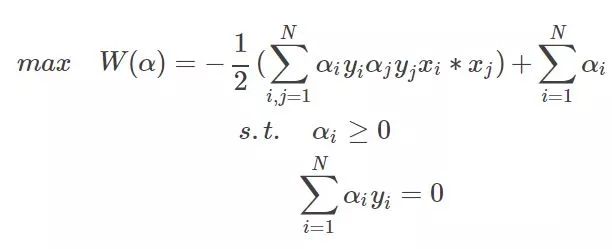
為什么有ai>0$,這是上節說到的KKT條件的必須。至此問題來源部分到這。
細心的你肯可能會發現,上述所有的構造等等都是在數據完全線性可分,且分界面完全將兩類分開,那么如果出現了下面這種情況:
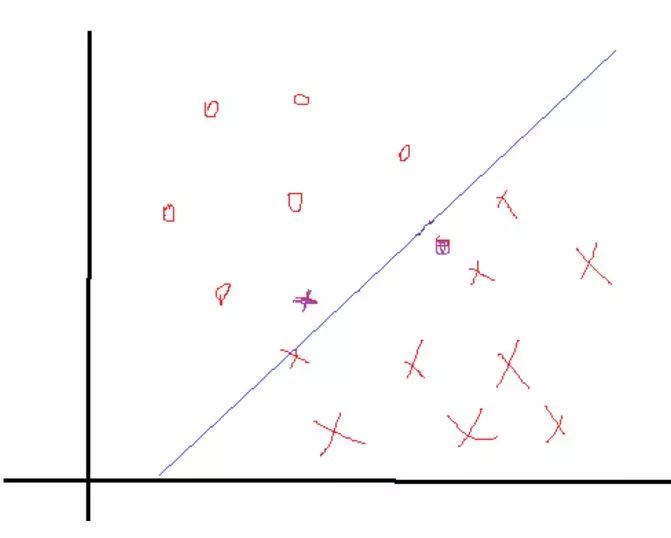
正負兩類的最遠點沒有明顯的分解面,搞不好正類的最遠點反而會跑到負類里面去了,負類最遠點跑到正類里面去了,要是這樣的話,你的分界面都找不到,因為你不可能找到將它們完全分開的分界面,那么這些點在實際情況是有的,就是一些離群點或者噪聲點,因為這一些點導致整個系統用不了。當然如果不做任何處理確實用不了,但是我們處理一下就可以用了。SVM考慮到這種情況,所以在上下分界面上加入松弛變量e,認為如果正類中有點到上界面的距離小于e,那么認為他是正常的點,哪怕它在上界面稍微偏下一點的位置,同理下界面。還是以上面的情況,我們目測下的是理想的分解面應該是下面這種情況:
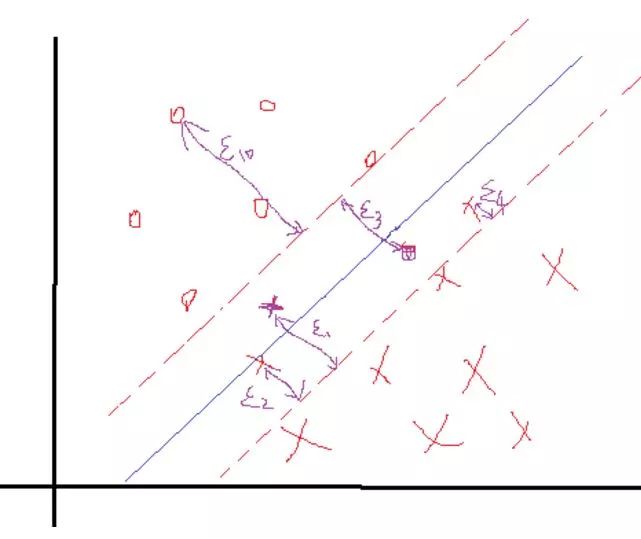
如果按照這種分會發現4個離群點,他們到自己對應分界面的距離表示如上,理論上講,我們給每一個點都給一個自己的松弛變量ei,如果一個分界面求出來了,那么比較這個點到自己對應的界面(上、下界面)的距離是不是小于這個值,要是小于這個值,就認為這個界面分的可以,比如上面的e3這個點,雖然看到明顯偏離了正軌,但是計算發現它的距離d小于等于我們給的e3,那么我們說這個分界面可以接受。你可能會說那像上面的e10,距離那么遠了,他肯定是大于預設給這個點的ei了對吧,確實是這樣的,但是我們還發現什么?這個點是分對了的點呀,所以你管他大不大于預設值,反正不用調整分界面。需要調整分界面的情況是只有當類似e3這樣的點的距離大于了e3的時候。

你發現目標函數里面多了一點東西,而加上這個是合理的,我們在優化的同時,也使得總的松弛變量之和最小。常數C決定了松弛變量之和的影響程度,如果越大,影響越嚴重,那么在優化的時候會更多的注重所有點到分界面的距離,優先保證這個和小。好了將問題寫在一起吧:


三、SMO算法原理與實戰求解
上節我們討論到解SVM問題最終演化為求下列帶約束條件的問題:
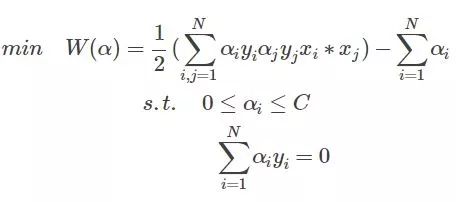
問題的解就是找到一組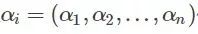 使得W最小。
使得W最小。
現在我們來看看最初的約束條件是什么樣子的:
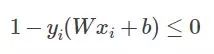
這是最初的一堆約束條件吧,現在有多少個約束條件就會有多少個αi。那么KKT條件的形成就是讓:
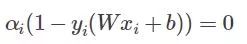
我們知道αi≥0,而后面那個小于等于0,所以他們中間至少有一個為0(至于為什么要這么做,第一節討論過)。再簡單說說原因,假設現在的分類問題如下:
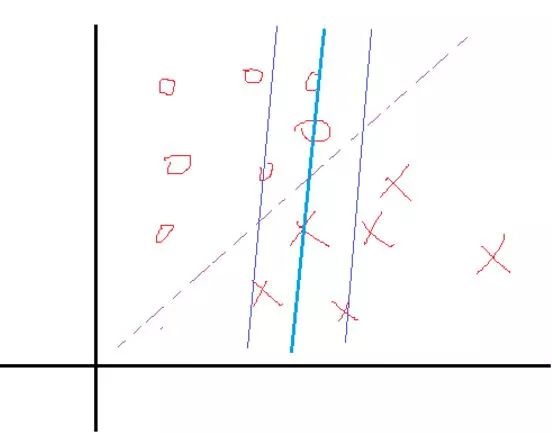
某一次迭代后,分類面為粗藍線所示,上下距離為1的分界面如細藍線所示,而理想的分界面如紫虛線所示。那么我們想想,要想把粗藍線變化到紫虛線,在這一次是哪些個點在起作用?很顯然是界于細藍線邊上以及它們之間的所有樣本點在起作用吧,而對于那些在細藍線之外的點,比如正類的四個圈和反類的三個叉,它們在這一次的分類中就已經分對了,那還考慮它們干什么?所以這一次就不用考慮這些分對了的點。那么我們用數學公式可以看到,對于在這一次就分對了的點,它們滿足什么關系,顯然yi(Wxi+b)>1,然后還得滿足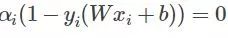 ,那么顯然它們的αi=0。對于那些在邊界內的點,顯然yi(Wxi+b)≤1,而這些點我們說是要為下一次達到更好的解做貢獻的,那么我們就取這些約束條件的極限情況,也就是yi(Wxi+b)=1,在這些極限約束條件下,我們就會得到一組新的權值W與b,也就是改善后的解。那么既然這些點的yi(Wxi+b)=1,那它對應的αi就可以不為0了,至于是多少,那就看這些點具體屬于分界面內的什么位置了,偏離的越狠的點,我想它對應的αi就越大,這樣才能把這個偏得非常狠的點給拉回來,或者說使其在下一次的解中更靠近正確的分類面。
,那么顯然它們的αi=0。對于那些在邊界內的點,顯然yi(Wxi+b)≤1,而這些點我們說是要為下一次達到更好的解做貢獻的,那么我們就取這些約束條件的極限情況,也就是yi(Wxi+b)=1,在這些極限約束條件下,我們就會得到一組新的權值W與b,也就是改善后的解。那么既然這些點的yi(Wxi+b)=1,那它對應的αi就可以不為0了,至于是多少,那就看這些點具體屬于分界面內的什么位置了,偏離的越狠的點,我想它對應的αi就越大,這樣才能把這個偏得非常狠的點給拉回來,或者說使其在下一次的解中更靠近正確的分類面。
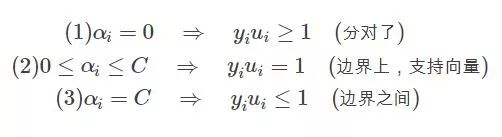
那么滿足KKT條件的,我們說如果一個點滿足KKT條件,那么它就不需要調整,一旦不滿足,就需要調整。由上可知,不滿足KKT條件的也有三種情況:





至此我們可以說,簡單的,線性的,帶有松弛條件(可以容錯的)的整個SMO算法就完了,剩下的就是循環,選擇兩個α,看是否需要更新(如果不滿足KKT條件),不需要再選,需要就更新。一直到程序循環很多次了都沒有選擇到兩個不滿足KKT條件的點,也就是所有的點都滿足KKT了,那么就大功告成了。
當然了,這里面還有些問題就是如何去優化這些步驟,最明顯的就是怎么去選擇這兩個α,程序越到后期,你會發現只有那么幾個點不滿足KKT條件,這個時候如果你再去隨機選擇兩個點的α,那么它是滿足的,就不更新,循環,這樣一直盲目的找呀找,程序的效率明顯就下來了。當然這在后面是有解決辦法的。
先不管那么多,就先讓他盲目盲目的找吧,設置一個代數,盲目到一定代數停止就ok了,下面就來一個盲目找α的matlab程序,看看我們的SMO算法如何。

我的樣本是這樣的:
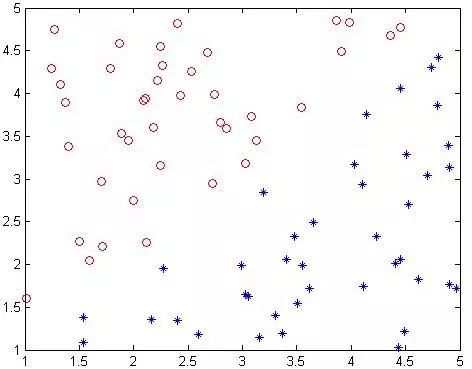
程序如下:
%%% * svm 簡單算法設計%%% 加載數據% * 最終data格式:m*n,m樣本數,n維度% * label:m*1 標簽必須為-1與1這兩類clcclearclose alldata = load('data_test2.mat');data = data.data;train_data = data(1:end-1,:)';label = data(end,:)';[num_data,d] = size(train_data);data = train_data;%% 定義向量機參數alphas = zeros(num_data,1);% 系數b = 0;% 松弛變量影響因子C = 0.6;iter = 0;max_iter = 40;%%while iter < max_iter ? ?alpha_change = 0; ? ?for i = 1:num_data ? ? ? ?%輸出目標值 ? ? ? ?pre_Li = (alphas.*label)'*(data*data(i,:)') + b; ? ? ? ?%樣本i誤差 ? ? ? ?Ei = pre_Li - label(i); ? ? ? ?% 滿足KKT條件 ? ? ? ?if (label(i)*Ei<-0.001 && alphas(i)
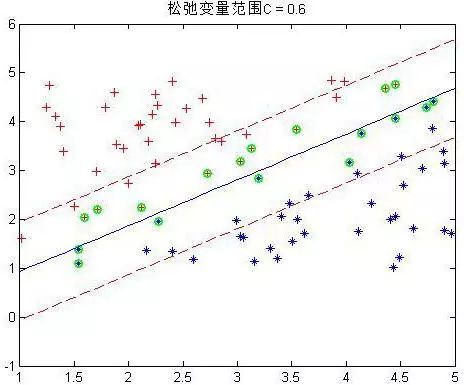
程序中設置了松弛變量前的系數C是事先規定的,表明松弛變量項的影響程度大小。下面是幾個不同C下的結果:
這是80個樣本點,matlab下還是挺快2秒左右就好了。上圖中,把真實分界面,上下范圍為1的界面,以及那些α不為0的點(綠色標出)都畫了出來,可以看到,C越大,距離越起作用,那么落在分界線之間的點就越少。同時可以看到,三種情況下,真實的分界面(藍色)都可以將兩種樣本完全分開(我的樣本并沒有重疊,也就是完全是可分的)。
好了,這就是隨機選取α的實驗,第一個α是按順序遍歷所有的α,第二個α是在剩下的α中在隨機選一個。當第二個α選了iter次還沒有發現不滿足KKT條件的,就退出循環。同時程序中的KKT條件略有不同,不過是一樣的。下面介紹如何進行啟發式的選取α呢?我們分析分析,比如上一次的一些點的α在0-C之間,也就是這些點不滿足條件需要調整,那么一次循環后,他調整了一點,在下一次中這些點是不是還是更有可能不滿足條件,因為每一次的調整比較不可能完全。而那些在上一次本身滿足條件的點,那么在下一次后其實還是更有可能滿足條件的。所以在啟發式的尋找α過程中,我們并不是遍歷所有的點的α,而是遍歷那些在0-C之間的α,而0-C反應到點上就是那些屬于邊界之間的點是不是。當某次遍歷在0-C之間找不到α了,那么我們再去整體遍歷一次,這樣就又會出現屬于邊界之間α了,然后再去遍歷這些α,如此循環。那么在遍歷屬于邊界之間α的時候,因為是需要選兩個α的,第一個可以隨便選,那第二個呢?這里在用一個啟發式的思想,第1個α選擇后,其對應的點與實際標簽是不是有一個誤差,屬于邊界之間α的所以點每個點都會有一個自己的誤差,這個時候選擇剩下的點與第一個α點產生誤差之差最大的那個點。
程序如下:
%%% * svm 簡單算法設計 --啟發式選擇%%% 加載數據% * 最終data格式:m*n,m樣本數,n維度% * label:m*1 標簽必須為-1與1這兩類clcclearclose alldata = load('data_test2.mat');data = data.data;train_data = data(1:end-1,:)';label = data(end,:)';[num_data,d] = size(train_data);data = train_data;%% 定義向量機參數alphas = zeros(num_data,1);b = 0;error = zeros(num_data,2);tol = 0.001;C = 0.6;iter = 0;max_iter = 40;%%alpha_change = 0;entireSet = 1;%作為一個標記看是選擇全遍歷還是部分遍歷while (iter < max_iter) && ((alpha_change > 0) || entireSet) alpha_change = 0; %% -----------全遍歷樣本------------------------- if entireSet for i = 1:num_data Ei = calEk(data,alphas,label,b,i);%計算誤差 if (label(i)*Ei<-0.001 && alphas(i)
其中的子函數,一個是計算誤差函數,一個是選擇函數如下:
function Ek = calEk(data,alphas,label,b,k)pre_Li = (alphas.*label)'*(data*data(k,:)') + b;Ek = pre_Li - label(k);
function [J,Ej] = select(i,data,num_data,alphas,label,b,C,Ei,choose)maxDeltaE = 0;maxJ = -1;if choose == 1 %全遍歷---隨機選擇alphas j = randi(num_data ,1); if j == i temp = 1; while temp j = randi(num_data,1); if j ~= i temp = 0; end end end J = j; Ej = calEk(data,alphas,label,b,J);else %部分遍歷--啟發式的選擇alphas index = find(alphas>0 & alphas < C); ? ?for k = 1:length(index) ? ? ? ?if i == index(k) ? ? ? ? ? ?continue; ? ? ? ?end ? ? ? ?temp_e = calEk(data,alphas,label,b,k); ? ? ? ?deltaE = abs(Ei - temp_e); %選擇與Ei誤差最大的alphas ? ? ? ?if deltaE > maxDeltaE maxJ = k; maxDeltaE = deltaE; Ej = temp_e; end end J = maxJ;end
至此算是完了,試驗了一下,兩者的效果其實差不多(反而隨機選取的效果更好一點,感覺是因為隨機保證了更多的可能,畢竟隨機選擇包括了你的特殊選擇,但是特殊選擇到后期是特殊不起來的,反而隨機會把那些差一點的選擇出來),但是速度上當樣本小的時候,基本上差不多,但是當樣本大的時候,啟發式的特殊選擇明顯占優勢了。我試驗了400個樣本點的情況,隨機選擇10多秒把,而啟發式2,3秒就好了。可見效果差不多的情況下,啟發式選擇是首要選擇。
至此兩種方式下的方法都實驗完了。那么我們看到,前面(三節)所講的一切以及實驗,分類的樣本都是線性樣本,那么如果來了非線性樣本該如何呢?而SVM的強大之處更在于對非線性樣本的準確劃分。那么前面的理論對于非線性樣本是否適用?我們又該如何處理非線性樣本呢?請看下節SVM非線性樣本的分類。
四、SVM非線性分類原理實驗
前面幾節我們討論了SVM原理、求解線性分類下SVM的SMO方法。本節將分析SVM處理非線性分類的相關問題。
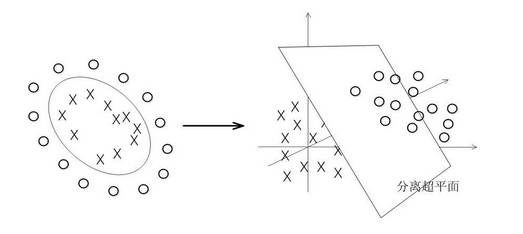
一般的非線性分類如下左所示(后面我們將實戰下面這種情況):
可以看到在原始空間中你想用一個直線分類面劃分開來是不可能了,除非圓。而當你把數據點映射一下成右圖所示的情況后,現在數據點明顯看上去是線性可分的,那么在這個空間上的數據點我們再用前面的SVM算法去處理,就可以得到每個數據點的分類情況了,而這個分類情況也是我們在低維空間的情況。也就是說,單純的SVM是不能處理非線性問題的,說白了只能處理線性問題,但是來了非線性樣本怎么辦呢?我們是在樣本上做的文章,我把非線性樣本變成線性樣本,再去把變化后的線性樣本拿去分類,經過這么一圈,就達到了把非線性樣本分開的目的,所以只看開頭和結尾的話發現,SVM竟然可以分非線性問題,其實呢還是分的線性問題。
現在的問題是如何找到這個映射關系對吧,就比如上面那個情況,我們可以人為計算出這種映射,比如一個樣本點是用坐標表示的(x1,x2),它有個類標簽,假設為1,那么把這個點映射到三維中變成
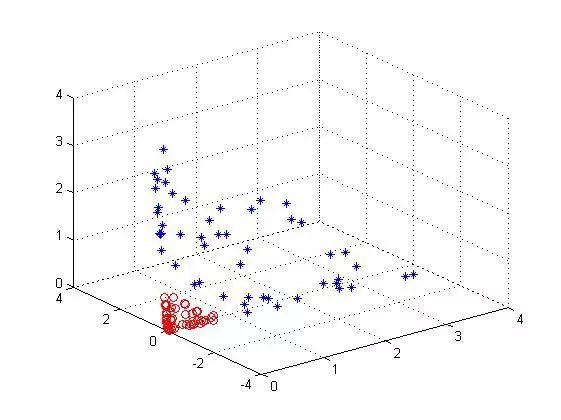
然后按照上面那個公式去把每個點映射成3維坐標點后,畫出來是這樣的:
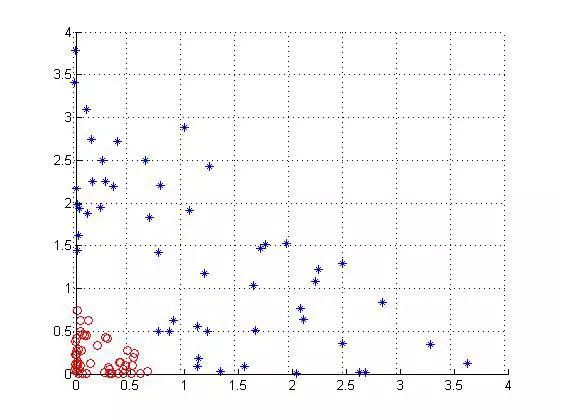
可以看到是線性可分的吧,如果還看不清把視角換個角度(右視圖):
現在能看清楚了吧。那這是二維的點到三維,映射的關系就是上面的那個關系,那如果是三維到四維,四維到N維呢?這個關系你還想去找嗎?理論上是找的到的,但是實際上人工去找你怎么去找?你怎么知道數據的映射關系是這樣的是那樣的?不可能知道。然而我們真的需要找到這種關系嗎?答案是不需要的,返回去看看前三節的關于SVM的理論部分可以看到,無論是計算a呀,還是b呀等等,只要涉及到原始數據點的,都是以內積的形式出來的,也就是說是一個點的向量與另一個點的向量相乘的,向量內積出來是一個值。
就拿a來更新來說,如下:
最后也是得到一個值比如C2。既然SVM里面所有涉及到原始數據的地方都是以向量的形式出現的,那么我們還需要管它的映射關系嗎?因為它也不需要你去計算說具體到比如說三維以后,三維里面的三個坐標值究竟是多少,他需要的是內積以后的一個結果值。那么好辦了,我就假設有一個黑匣子,輸入原始數據維度下的兩個坐標向量,然后經過黑匣子這么一圈,出來一個值,這個值我們就認為是高維度下的值。而黑匣子的潛在意義就相當于一個高維映射器一樣。更重要的是我們并不需要知道黑匣子究竟是怎么映射的,只需要知道它的低緯度下的形式就可以了。常用的黑匣子就是徑向基函數,而這個黑匣子在數學上就叫做核函數,例如徑向基函數的外在形式如下所示:
o是需要預先設定的參數。至于這個黑匣子把初始數據映射到多少維了,誰知道呢,既然是黑匣子,那就是看不到的,上帝給了人類這么一個黑匣子就已經很夠意思了。可以看到的是原始數據結果黑匣子算了以后,出來就是一個值了,而這個值就認為是高維度下的數據通過內積計算而來的值。當然上帝還留了一個窗戶,就是o,相傳o選取的越小,數據映射的維度越大,小到一定程度,維度空間大到無窮維。反之越大,映射的維度空間就越小,但是會不會小到低于原始空間維度呢?誰知道了,然而通過實驗我發現,大到一定程度,樣本點分的亂七八糟,并且o正好在一定范圍的時候效果非常好,這個范圍既不是極小的范圍,也不是極大的范圍,那這暗示了什么呢?也就是說非線性原始樣本是有一個屬于他自己的最佳高維空間的,大了小了似乎都不好。
好了既然黑匣子是藏著的,那也就只能說這么多了。有趣的是上帝給的這個黑匣子不止一個,有好幾個,只是上面的那個普遍效果更好而已。基于此,那么對于上節的SMO算法,如果拿來求解非線性數據的話,我們只需要將其中對應的內積部分改成核函數的形式即可。一個數據核函數程序如下:
function result = Kernel(data1,data2,sigma)% data里面每一行數據是一個樣本(的行向量)[m1,~] = size(data1);[m2,~] = size(data2);result = zeros(m1,m2);for i = 1:m1 for j = 1:m2 result(i,j) = exp(-norm(data1(i,:)-data2(j,:))/(2*sigma^2)); endend
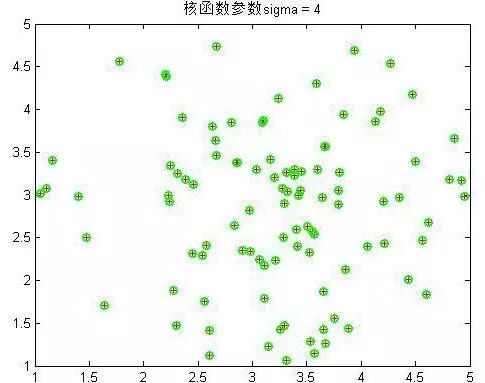
有了此核函數,我們用上節的隨機遍歷αα的方式(這個函數代碼少一點)來實驗一下非線性樣本,非線性樣本如下:然后把主程序對應的部分用上述核函數代替:
%%% * svm 簡單算法設計%%% 加載數據% * 最終data格式:m*n,m樣本數,n維度% * label:m*1 標簽必須為-1與1這兩類clcclear% close alldata = load('data_test1.mat');data = data.data;train_data = data(1:end-1,:)';label = data(end,:)';[num_data,d] = size(train_data);data = train_data;%% 定義向量機參數alphas = zeros(num_data,1);% 系數b = 0;% 松弛變量影響因子C = 0.6;iter = 0;max_iter = 80;% 核函數的參數sigma = 4;%%while iter < max_iter ? ?alpha_change = 0; ? ?for i = 1:num_data ? ? ? ?%輸出目標值 ? ? ? ?pre_Li = (alphas.*label)'*Kernel(data,data(i,:),sigma) + b; ? ? ? ?%樣本i誤差 ? ? ? ?Ei = pre_Li - label(i); ? ? ? ?% 滿足KKT條件 ? ? ? ?if (label(i)*Ei<-0.001 && alphas(i)
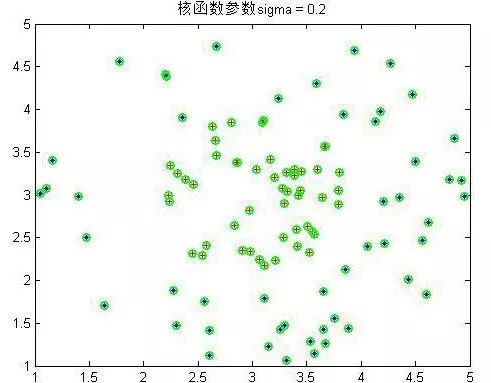
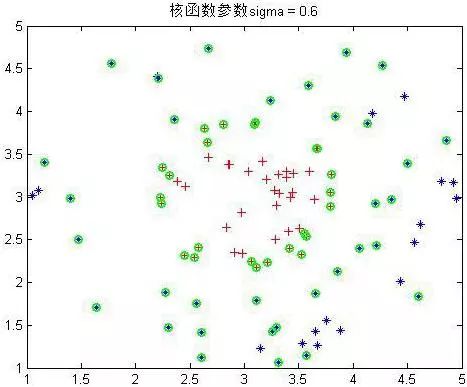
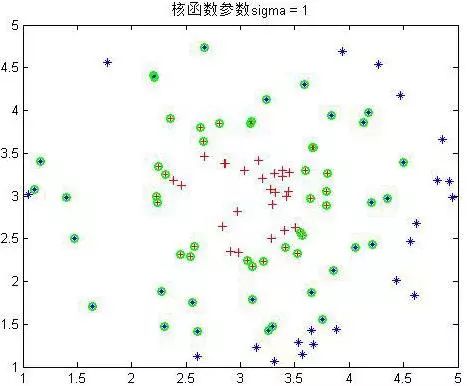
下面是幾個不同參數下的結果:
可以看到σ到4以后就分不出來了。綠色的為支持向量,可以看到在σ在0.6到1之間是最少的,結果應該也是最好的。至此SMO實驗非線性樣本完畢。
當今學者已經有非常多的人研究SVM算法,同時開發了許多開源的程序,這些程序都是經過不斷優化的,性能比起我們這里自己編的來說要好得多,所以在實際應用中通常都是用他們無私貢獻的軟件包。一個典型的軟件包就是***一個教授團隊的LIBSVM軟件包,那么你是否想一窺其用法,看看它的性能如何呢?請看下節matlab下LIBSVM的簡單使用。
五、MATLAB下libsvm的簡單使用:分類與回歸
本節簡單介紹一下libsvm的使用方法。關于libsvm似乎曾經使用過,那個時候主要用libsvm進行簡單的人臉識別實驗。
1)介紹與分類實驗
那么現在最新版本的libsvm為3.2.0,下載地址如下:http://www.csie.ntu.edu.tw/~cjlin/libsvm/
下載下來的libsvm其實包含好多個平臺的工具箱軟件,c++,matlab,java,python都有。他們的函數使用方法是一樣的。
那么在下載完以后,點擊里面的matlab下平臺,直接在點擊里面的make.m函數就可以了。正常情況下如果你的matlab含有編譯平臺的話直接就可以運行了,如果沒有,還需要選擇一個平臺 mex -setup 。小提醒一下,這個編譯過程不要在c盤下使用,也就是libsvm先不要放在c盤,涉及到權限,機器不讓編譯。編譯完后在matlab的設置路徑中添加進去編譯的文件夾及其內容,那么就可以使用了。正常編譯的過程是這樣的: 在上面的人臉識別實驗中曾經介紹過里面的主要函數,這里為了放在一塊,把那里的拿過來吧:
目前版LIBSVM(3.2.0)在matlab下編譯完后只有四個函數,libsvmread,Libsvmwrite,svmtrain(matlab自帶的工具箱中有一個同名的函數),svmpredict。
libsvmread主要用于讀取數據
這里的數據是非matlab下的.mat數據,比如說是.txt,.data等等,這個時候需要使用libsvmread函數進行轉化為matlab可識別數據,比如自帶的數據是heart_scale數據,那么導入到matlab有兩種方式,一種使用libsvmread函數,在matlab下直接libsvmread(heart_scale);第二種方式為點擊matlab的‘導入數據’按鈕,然后導向heart_scale所在位置,直接選擇就可以了。個人感覺第二種方式超級棒,無論對于什么數據,比如你在哪個數據庫下下載的數據,如何把它變成matlab下數據呢?因為有的數據libsvmread讀取不管用,但是‘導入數據’后就可以變成matlab下數據。
libsvmwrite寫函數,就是把已知數據存起來
使用方式為:libsvmwrite(‘filename’,label_vector, instance_matrix);label_vector是標簽,instance_matrix為數據矩陣(注意這個數據必須是稀疏矩陣,就是里面的數據不包含沒用的數據(比如很多0),有這樣的數據應該去掉再存)。
svmtrain訓練函數,訓練數據產生模型的
一般直接使用為:model=svmtrain(label,data,cmd); label為標簽,data為訓練數據(數據有講究,每一行為一個樣本的所有數據,列數代表的是樣本的個數),每一個樣本都要對應一個標簽(分類問題的話一般為二分類問題,也就是每一個樣本對應一個標簽)。cmd為相應的命令集合,都有哪些命令呢?很多,-v,-t,-g,-c,等等,不同的參數代表的含義不同,比如對于分類問題,這里-t就表示選擇的核函數類型,-t=0時線性核。-t=1多項式核,-t=2,徑向基函數(高斯),-t=3,sigmod核函數,新版出了個-t=4,預計算核(還不會用);-g為核函數的參數系數,-c為懲罰因子系數,-v為交叉驗證的數,默認為5,這個參數在svmtrain寫出來使用與不寫出來不使用的時候,model出來的東西不一樣,不寫的時候,model為一個結構體,是一個模型,可以帶到svmpredict中直接使用,寫出來的時候,出來的是一個訓練模型的準確率,為一個數值。一般情況下就這幾個參數重要些,還有好多其他參數,可以自己參考網上比較全的,因為下面的這種方法的人臉識別就用到這么幾個參數,其他的就不寫了。
svmpredict訓練函數,使用訓練的模型去預測來的數據類型。
使用方式為:
[predicted_label,accuracy,decision_values/prob_estimates]= svmpredict(testing_label_vector,testing_instance_matrix,model,’libsvm_options’)
或者:
[predicted_label]=svmpredict(testing_label_vector,testing_instance_matrix, model, ‘libsvm_options’)
第一種方式中,輸出為三個參數,預測的類型,準確率,評估值(非分類問題用著),輸入為測試類型(這個可與可無,如果沒有,那么預測的準確率accuracy就沒有意義了,如果有,那么就可以通過這個值與預測出來的那個類型值相比較得出準確率accuracy,但是要說明一點的是,無論這個值有沒有,在使用的時候都得加上,即使沒有,也要隨便加上一個類型值,反正你也不管它對不對,這是函數使用所規定的的),再就是輸入數據值,最后是參數值(這里的參數值只有兩種選擇,-p和-b參數),曾經遇到一個這樣的問題,比如說我在訓練函數中規定了-g參數為0.1,那么在預測的時候是不是也要規定這個參數呢?當你規定了以后,程序反而錯誤,提醒沒有svmpredict的-g參數,原因是在svmtrain后會出現一個model,而在svmpredict中你已經用了這個model,而這個model中就已經包含了你所有的訓練參數了,所以svmpredict中沒有這個參數,那么對于的libsvm_options就是-p和-b參數了。對于函數的輸出,兩種方式調用的方法不一樣,第一種調用把所有需要的數據都調用出來了,二第二種調用,只調用了predicted_label預測的類型,這里我們可以看到,在單純的分類預測模型中,其實第二種方式更好一些吧,既簡單有實用。
致此,四個函數在分類問題中的介紹大概如此,當然還有很多可以優化的細節就不詳細說了,比如可以再使用那些參數的時候,你如果不規定參數的話,所有的-參數都是使用默認的,默認的就可能不是最好的吧,這樣就涉及到如何去優化這個參數了。
使用就介紹到這里吧,下面實戰一下,樣本集選擇前面使用的200個非線性樣本集,函數如下:
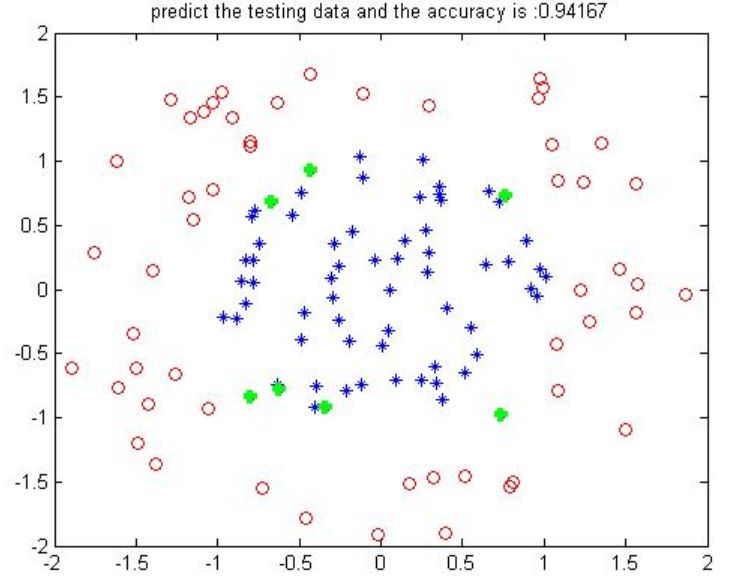
%%% * libsvm 工具箱簡單使用%%% 加載數據% * 最終data格式:m*n,m樣本數,n維度% * label:m*1 標簽為-1與1這兩類clcclearclose alldata = load('data_test1.mat');data = data.data';%選擇訓練樣本個數num_train = 80;%構造隨機選擇序列choose = randperm(length(data));train_data = data(choose(1:num_train),:);gscatter(train_data(:,1),train_data(:,2),train_data(:,3));label_train = train_data(:,end);test_data = data(choose(num_train+1:end),:);label_test = test_data(:,end);predict = zeros(length(test_data),1);%% ----訓練模型并預測分類model = svmtrain(label_train,train_data(:,1:end-1),'-t 2');% -t = 2 選擇徑向基函數核 true_num = 0;for i = 1:length(test_data) % 作為預測,svmpredict第一個參數隨便給個就可以 predict(i) = svmpredict(1,test_data(i,1:end-1),model);end%% 顯示結果figure;index1 = find(predict==1);data1 = (test_data(index1,:))';plot(data1(1,:),data1(2,:),'or');hold onindex2 = find(predict==-1);data2 = (test_data(index2,:))';plot(data2(1,:),data2(2,:),'*');hold onindexw = find(predict~=(label_test));dataw = (test_data(indexw,:))';plot(dataw(1,:),dataw(2,:),'+g','LineWidth',3);accuracy = length(find(predict==label_test))/length(test_data);title(['predict the testing data and the accuracy is :',num2str(accuracy)]);
可以看到,關于svm的部分就那么一點,其他的都是輔助吧,那么一個結果如下:
數據人為設置了一些重疊,這個結果算是非常好了。當然對于libsvm函數,里面還有許多細節,像參數選擇等等,不同的參數結果是不一樣的,這就待你去探究了。
2)回歸實驗
回歸問題不像分類問題,回歸問題相當于根據訓練樣本訓練出一個擬合函數一樣,可以根據這個擬合函數可以來預測給定一個樣本的輸出值。可以看到分類問題輸出的是樣本所屬于的類,而回歸問題輸出的是樣本的預測值。
常用的地方典型的比如股票預測,人口預測等等此類預測問題。
libsvm同樣可以進行回歸預測,所需要改變的只是里面的參數設置。查看libsvm的官網介紹參數詳情如下:
options:-s svm_type : set type of SVM (default 0) 0 -- C-SVC 1 -- nu-SVC 2 -- one-class SVM 3 -- epsilon-SVR 4 -- nu-SVR-t kernel_type : set type of kernel function (default 2) 0 -- linear: u'*v 1 -- polynomial: (gamma*u'*v + coef0)^degree 2 -- radial basis function: exp(-gamma*|u-v|^2) 3 -- sigmoid: tanh(gamma*u'*v + coef0)-d degree : set degree in kernel function (default 3)-g gamma : set gamma in kernel function (default 1/num_features)-r coef0 : set coef0 in kernel function (default 0)-c cost : set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)-n nu : set the parameter nu of nu-SVC, one-class SVM, and nu-SVR (default 0.5)-p epsilon : set the epsilon in loss function of epsilon-SVR (default 0.1)-m cachesize : set cache memory size in MB (default 100)-e epsilon : set tolerance of termination criterion (default 0.001)-h shrinking: whether to use the shrinking heuristics, 0 or 1 (default 1)-b probability_estimates: whether to train a SVC or SVR model for probability estimates, 0 or 1 (default 0)-wi weight: set the parameter C of class i to weight*C, for C-SVC (default 1)
可以看到-s svm_type 控制的就是訓練類型,而當-s等于3或4的時候,就是回歸模型SVR。
-s 3 就是常用的帶懲罰項的 SVR模型,我們用這個實驗。我使用的是libsvm3.2.0工具箱,版本不同可能會帶來調用方式的不同。測試實驗的代碼如下,可能會有一些細節需要自己去探索:
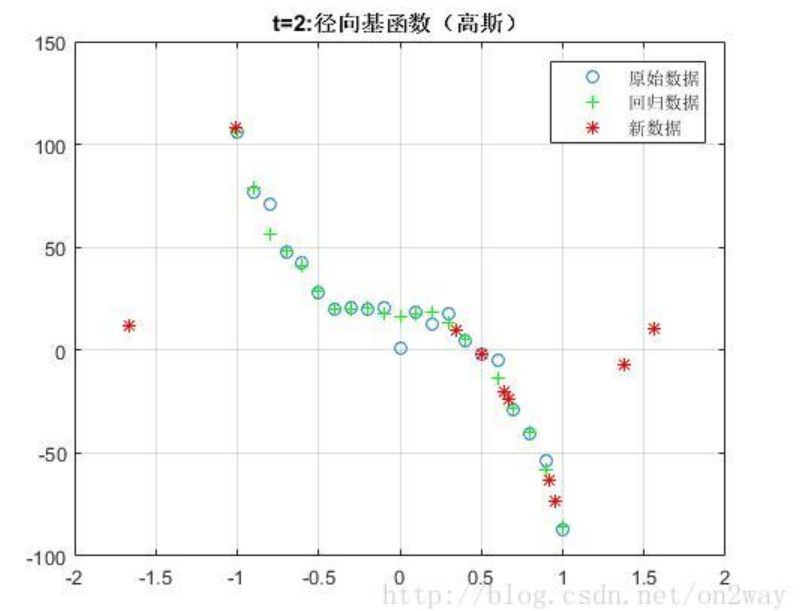
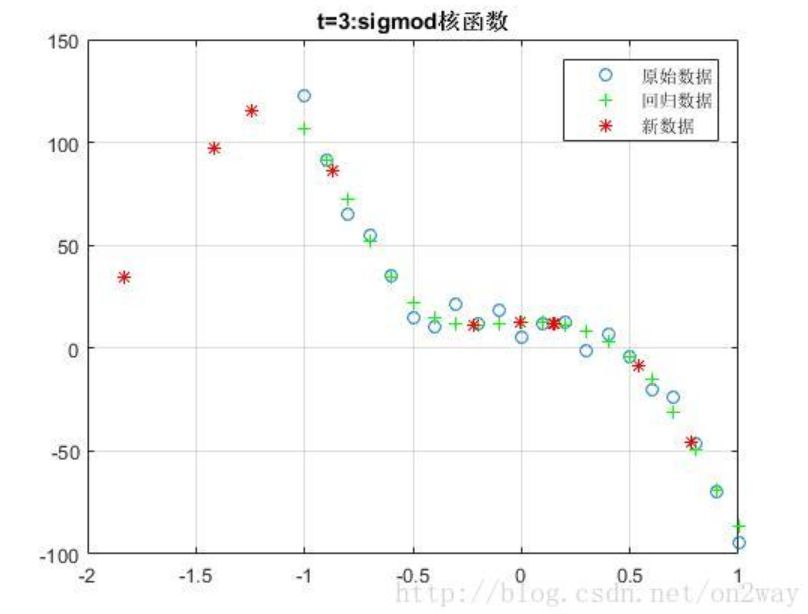
close all;clear;clc;%%% 生成待回歸的數據x = (-1:0.1:1)';y = -100*x.^3 + x.^2 - x + 1;% 加點噪聲y = y+ 20*rand(length(y),1);%% 采用交叉驗證選擇參數mse = 10^7;for log2c = -10:0.5:3, for log2g = -10:0.5:3, % -v 交叉驗證參數:在訓練的時候需要,測試的時候不需要,否則出錯 cmd = ['-v 3 -c ', num2str(2^log2c), ' -g ', num2str(2^log2g) , ' -s 3 -p 0.4 -t 3']; cv = svmtrain(y,x,cmd); if (cv < mse), ? ? ? ? ? ?mse = cv; bestc = 2^log2c; bestg = 2^log2g; ? ? ? ?end ? ?endend%% ?訓練--cmd = ['-c ', num2str(2^bestc), ' -g ', num2str(2^bestg) , ' -s 3 -p 0.4 -n 0.1'];model = svmtrain(y,x,cmd);% model% 利用建立的模型看其在訓練集合上的回歸效果% 注意libsvm3.2.0的svmpredict函數必須有三個參數輸出[py,~,~] = svmpredict(y,x,model);figure;plot(x,y,'o');hold on;plot(x,py,'g+');%% % 進行預測新的x值%-- 產生[-1 1]的隨機數testx = -2+(2-(-2))*rand(10,1);testy = zeros(10,1);% 理論y值無所謂[ptesty,~,~] = svmpredict(testy,testx,model);hold on;plot(testx,ptesty,'r*');legend('原始數據','回歸數據','新數據');grid on;% title('t=0:線性核')% title('t=1:多項式核')% title('t=2:徑向基函數(高斯)')title('t=3:sigmod核函數')
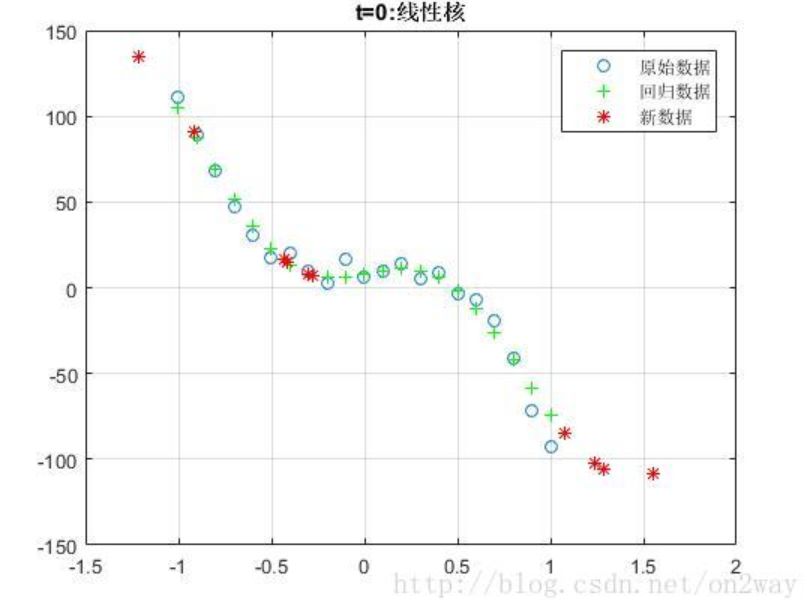
這里我隨機生成一個3次函數的隨機數據,測試了幾種不同svm里面的核函數:
因為我們的數據是由三次函數模擬生成的,所以可以看到,在這種情況下使用線性核t=0時候效果更好,然而實際情況下一般我們也不知道數據的分布函數,所以在選擇核函數的時候還是需要多實驗,找到最適合自己數據的核函數。
這里采用了交叉驗證的方式自適應選擇模型中重要的兩個參數,需要注意的是參數的范圍,不要太大,步長可能也需要控制,否則在數據量很大的時候需要運行很久。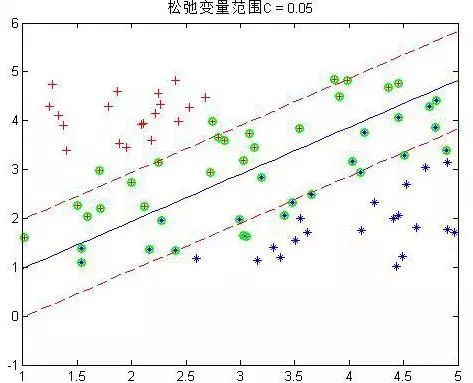

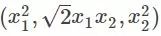 ,對每個點我都這么去映射,假設一個原始點樣本集是這樣的:?
,對每個點我都這么去映射,假設一個原始點樣本集是這樣的:?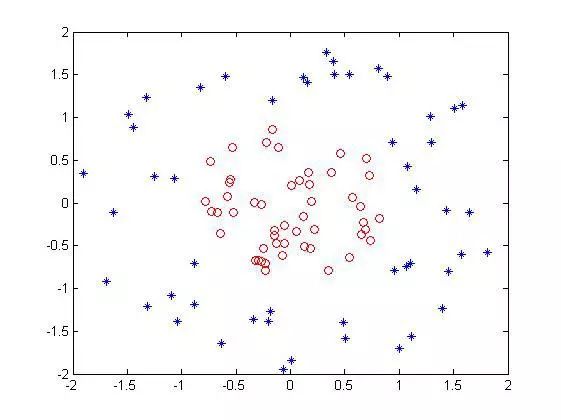

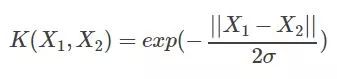

-
SVM
+關注
關注
0文章
154瀏覽量
32479 -
kkt
+關注
關注
0文章
4瀏覽量
4007
原文標題:SVM大解密(附代碼和公式)
文章出處:【微信號:AI_Thinker,微信公眾號:人工智能頭條】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
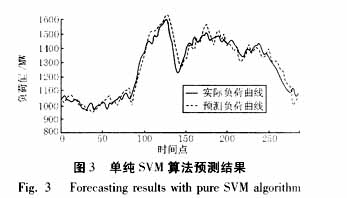
SVM與Fourier算法在電網短期負荷預測中的應用
基于MapReduce的SVM態勢評估算法
支持向量機SVM算法在智能交通系統中的應用綜述





 SVM算法附代碼和公式詳細概述
SVM算法附代碼和公式詳細概述












評論