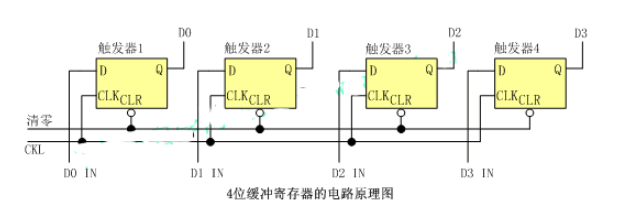
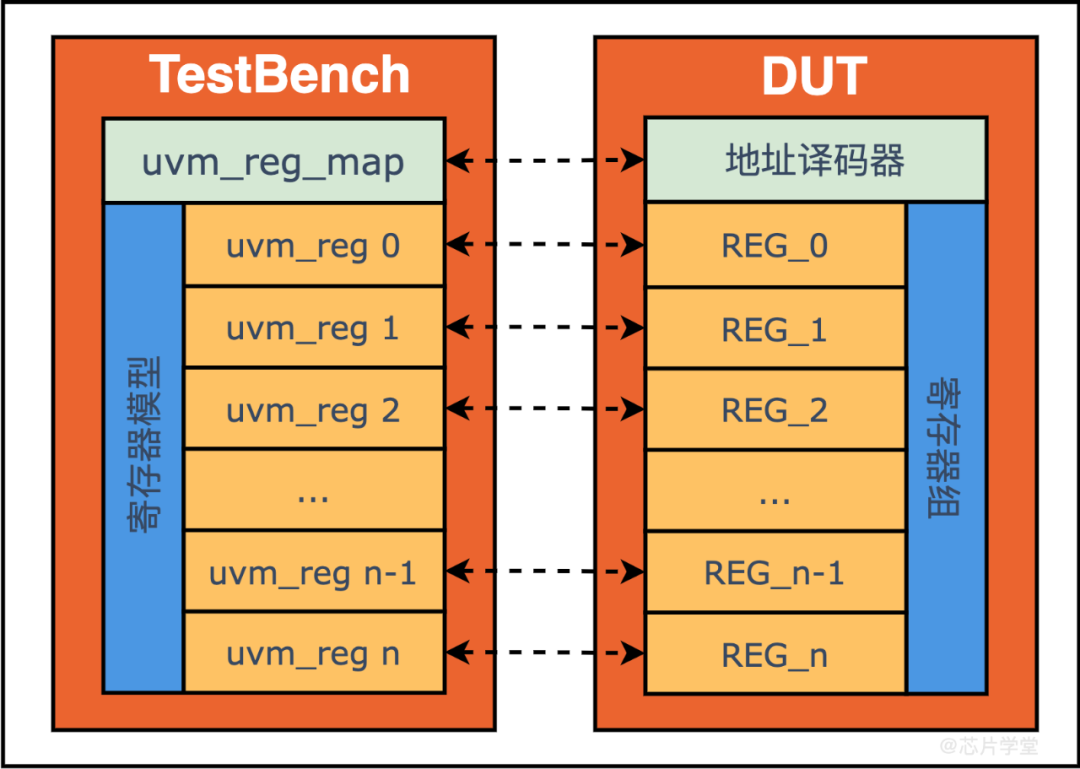
Abstract: The DS3514 programmable gamma and VCOM voltage generator features gamma buffers that provide 10 bits of resolution. These 10 bits are stored in two 8-bit registers. This application note explains how to calculate the register values for the gamma registers.
The example below shows how the 10 bits are assigned to the two registers. This example uses the latch A register for GM1, which is addresses 02h and 03h. The most significant byte (MSB) is address 02h, and the least significant byte (LSB) is address 03h. The 6 "don't care" bits in the LSB are read back as 0s.
The following two methods can be used to obtain the correct data to write to these registers.
The data for the MSB is obtained by dividing the decimal value by 4, with no remainder or rounding. This is equivalent to dividing the hex value by 04h or shifting the binary value right 2 bits. The data for the LSB is obtained by ANDing the original desired setting with 0x003 (00 0000 0011), then shifting this result left 6 bits (multiply by 64 or 40h).

Introduction
The DS3514 programmable gamma and VCOM voltage generator has gamma buffers with 10 bits of resolution. This means that there are 1024 possible gamma output levels. The range of settings for these gamma registers in decimal is 0 to 1023 (000h to 3FFh). This 10-bit value is stored left-justified in two 8-bit registers.The example below shows how the 10 bits are assigned to the two registers. This example uses the latch A register for GM1, which is addresses 02h and 03h. The most significant byte (MSB) is address 02h, and the least significant byte (LSB) is address 03h. The 6 "don't care" bits in the LSB are read back as 0s.
| Reg Add | Bit 7 | ? | ? | ? | ? | ? | ? | Bit 0 |
| 02h | Bit 9 | Bit 8 | Bit 7 | Bit 6 | Bit 5 | Bit 4 | Bit 3 | Bit 2 |
| 03h | Bit 1 | Bit 0 | X | X | X | X | X | X |
The following two methods can be used to obtain the correct data to write to these registers.
Method 1
The first method calculates the MSB and the LSB at the same time. First, multiply the desired decimal setting (0 to 1023) by 64 or multiply the hex setting (000h-3FFh) by 40h. Alternatively, the binary value can be shifted left six times.Example 1
Desired setting: dec = 472; hex = 1D8h; bin = 01 1101 1000 472 × 64 = 30208 = 0111 0110 0000 0000 1D8h × 40h = 7600h = 0111 0110 0000 0000 Shift binary left 6 bits = 0111 0110 0000 0000
Example 2
Desired setting: dec = 799; hex = 31Fh; bin = 11 0001 1111 799 × 64 = 51136 = 1100 0111 1100 0000 31Fh × 40h = C7C0h = 1100 0111 1100 0000 Shift binary left 6 bits = 1100 0111 1100 0000This 16-bit word can now be broken into two bytes, the MSB and LSB. From example 1, the most significant byte is 76h, which will be written to register 02h; the least significant byte is 00h, which will be written to register 03h.
Method 2
This method calculates the MSB and LSB independent of each other. How this method is implemented in code will vary depending on which programming language is used.The data for the MSB is obtained by dividing the decimal value by 4, with no remainder or rounding. This is equivalent to dividing the hex value by 04h or shifting the binary value right 2 bits. The data for the LSB is obtained by ANDing the original desired setting with 0x003 (00 0000 0011), then shifting this result left 6 bits (multiply by 64 or 40h).
Example 3
Desired setting: dec = 799; hex = 31Fh; bin = 11 0001 1111 MSB calculation: 799/4 = 199 = C7h = 1100 0111 31Fh/04h = C7h = 1100 0111 Data shifted right 2 bits = 1100 0111 LSB calculation: AND data with 03h 31Fh AND 003h = 003h 11 0001 1111 AND 00 0000 0011 = 00 0000 0011 Data shifted left 6 bits (multiply by 64 or 40h) 3 × 64 = 192 = C0h = 1100 0000 003h × 40h = C0h = 1100 0000 0000 0011 shifted left 6 bits = 1100 0000
Programming the Gamma Data
Below is a diagram showing how the data from example 3 can be written to registers 02h and 03h of the DS3514 using I2C communication. This programming assumes that the A0 pin is grounded, thus making the DS3514 slave address C0h. In this example, register 02h is written to C7h and register 03h is written to C0h. This data can also be written using single-byte writes.
 電子發燒友App
電子發燒友App
























評論