現行的網絡安全傳輸方案中經典的方法分為對稱加密和非對稱加密2種。對稱加密運算速度快但容易被攻擊和破解；非對稱加密算法復雜，不易被破解，但加密速度慢，不適宜傳輸大量的安全數據。通過對哈夫曼壓縮方法研究可知，不同的數據文件經過哈夫曼壓縮后可形成不同的少量數據的哈夫曼壓縮編碼表和壓縮文件。通過對哈夫曼編碼表進行非對稱加密設計的方案，可以減少非對稱加密算法加密的字節數，實現大數據量文件的非對稱加密。同時通過對大數據文件的壓縮，可以減少整個文件大小，提高網絡傳輸效率。該方案已在多個網絡安全傳輸項目中得到應用，完全能夠滿足網絡傳輸安全要求。

　　近年來，隨著計算機和網絡技術的迅速發展，越來越多的社會團體、機關、企事業單位建立了計算機網絡，人們更多的將社會活動、辦公以及科研等各個方面活動的重心轉移到了網絡當中，形成了由局域網絡為節點組成的龐大的互聯網絡。在互聯網絡節點之間越來越多的數據交換任務需要完成，以實現計算機軟、硬件資源和信息資源的共享。在互聯網絡這種開放系統中進行數據交換，對于安全級別要求較高的數據，傳輸過程中的數據安全是至關重要的。

　　網絡數據傳輸安全的核心是通過對數據發送、網絡傳輸、數據接收各個環節中的數據進行加密處理，以達到實現數據安全的目的。保護在公用網絡信息系統中傳輸、交換和存儲的數據的保密性、完整性、真實性、可靠性、可用性和不可抵賴性等。而加密技術則是數據傳輸安全的核心。它通過加密算法將數據從明文加密為密文并進行通信，密文即使被黑客截取也很難被破譯，然后通過對應解碼技術解碼密文還原明文。

　　目前國際上通用的加密方法主要有對稱加密和不對稱加密，不同的加密方法有不同的特點，在數據傳輸高安全性要求比較高的網絡系統中得到了普遍采用，例如電子商務、郵件傳輸等方面。

　　1 加密算法的現狀

　　密碼學是為了保證在發送者和接收者之間傳遞的數據不被第三者獲得而對要傳遞的數據進行加密使其獲得保密的科學。通常將傳遞的數據稱為明文，為了保護明文，以將其通過某種方式變換成無法識別的密文，這個變換過程稱為加密；另一方面密文可以通過相應的逆變換再還原成明文，這個過程稱為解密。

　　加密算法可以看作是一個復雜的函數變換：

　　C=F(M，Key)

　　式中：C代表密文，即加密后得到的字符序列；M代表明文，即待加密的字符序列；Key表示密鑰，是秘密選定的一個字符序列。

　　當加密完成后，可以將密文通過不安全渠道送給數據接收人，只有擁有解密密鑰的數據接收人才可以對密文進行解密，即反變換得到明文。密鑰的傳遞必須通過安全渠道。

　　目前通用的加密算法主要分為對稱和非對稱算法。對稱算法采用相同的密鑰進行加密和解密。常用的對稱加密算法有AES、IDEA、RC2／RC4、DES 等，其最大的困難是密鑰分發問題，必須通過當面或在公共傳送系統中使用安全的方法交換密鑰。對稱加密由于加密速度快、硬件容易實現、安全強度高，因此仍被廣泛用來加密各種信息。但對稱加密也存在著固有的缺點：密鑰更換困難，經常使用同一密鑰進行數據加密，給攻擊者提供了攻擊密鑰的信息和時間。非對稱算法，采用公鑰進行加密而利用私鑰進行解密。公鑰是可以公開的，任何人都可以獲得，數據發送人用公鑰將數據加密后再傳給數據接收人，接收人用自己的私鑰解密。非對稱加密的安全性主要依賴難解的數學問題，密鑰的長度比對稱加密大得多，因此加密效率較低，主要使用在身份認證、數字簽名等領域。非對稱加密的加密速度慢，對于大量數據的加密傳輸是不適合的。非對稱加密算法包括RSA、DH、EC、DSS等。目前比較流行的、最有名的非對稱加密算法是RSA。

　　RSA的安全性在于大整數因子分解的難度，其體制構造是基于數論的歐拉定理，產生公開密鑰和秘密密鑰的方法為：

　　(1)取2個互異的大素數p和q；

　　(2)計算n=p×q；

　　(3)隨機選取整數e，且e與(p-1)×(q-1)互為素數；

　　(4)另找一個數d，使其滿足(e×d)mod[(p-1)×(q-1)]=1；(n，e)即為公鑰；(n，d)為私鑰。對于明文M，用公鑰(n，e)加密可得到密文C，C=Me mod n；對于密文C，用私鑰(n，d)解密可得到明文M，M=Cd mod n。

　　利用當今可預測的計算能力，在十進制下，分解2個250位質數的積要用數十萬年的時間，并且質數用盡或2臺計算機偶然使用相同質數的概率小到可以被忽略。由此可見，企圖利用公鑰和密文推斷出明文或者企圖利用公鑰推斷出私鑰的難度極其巨大，幾乎是不可行的。因此，這種機制為信息傳輸提供了很高的安全保障。

　　由上述內容可以發現，無論是對稱加密和非對稱加密的過程都是完成如下的過程：

　　(1)產生密鑰key；

　　(2)C=F(M，Key)，即使用已經產生的密鑰，通過加密算法將明文轉換為密文。

　　(3)數據傳輸；

　　(4)M=F’(C，key)，即接收方使用解密算法，將密文轉換為明文。

　　如果需要傳輸的明文數據龐大，則加密和解密的算法的耗時將非常長，并且數據傳輸時也會占用大量的網絡資源。也就是以上的(2)，(3)，(4)三個過程都會占用大量的時間和資源，如果能夠降低這3個過程的時間，就會節省大量的資源，提高數據傳輸的效率。通過使用哈夫曼編碼對文件進行壓縮，就可以大大降低以上3個環節的處理時間，并同時在傳輸處理過程中減少計算機資源和網絡資源的占用。

　　2 哈夫曼編碼介紹

　　哈夫曼編碼是20世紀50年代由哈夫曼教授研制開發的，它借助了數據結構當中的樹型結構，在哈夫曼算法的支持下構造出一棵最優二叉樹，把這類樹命名為哈夫曼樹。因此，準確地說，哈夫曼編碼是在哈夫曼樹的基礎之上構造出來的一種編碼形式，它的本身有著非常廣泛的應用。

　　2．1 基本原理

　　數據能夠被壓縮的理論依據如下：

　　定義1? 對于給定的信源和碼符號集，若有一個惟一可譯碼，其平均碼長L小于所有其他惟一可譯碼，則稱這種碼為緊致碼或最佳碼。

　　定理1? 哈夫曼編碼是緊致碼。

　　計算機文件是以字節為單位組成的，每個字節的取值為O～255。每個字節都看成字符，共256種字符。因此，每個字節都是以8個二進制位的定長編碼表示的。由于這種定長碼也是惟一可譯碼，根據定理1有L≤8。

　　設某個文件有N個字節組成，則該文件總長度為8N比特。如果對該文件進行哈夫曼編碼，則該文件總長度為LN比特。由于L≤8，所以LN≤8。所以，只要文件滿足L<8，用哈夫曼編碼總可以對其壓縮。

　　哈夫曼編碼是一種變長編碼，即通過使用較短的碼字來給出現概率較高的信源符號編碼，而出現概率較小的信源符號用較長的碼字來編碼，從而使平均碼長最短，達到最佳編碼的目的。由于哈夫曼編碼只能對概率已知的信源符號編碼，因此是一種統計編碼。

　　2．2 構造哈夫曼編碼表

　　獲得一個文件的哈夫曼編碼表是該文件獲得壓縮與解壓的關鍵。設某個文件中含有q種字符S1，S2，…，Sq，并且統計出每種字符在文件中出現的概率分別為p(S1)，p(S2)，…，p(Sq)，則編碼的具體方法如下：

　　(1)將q個信源符號按概率大小遞減排列p(S1)≥p(S2)≥…≥p(Sq)；

　　(2)用字符‘O’和‘1’分別代表概率最小的2個信源符號，并將這2個概率最小的信源符號合并成1個信源符號，從而得到只包含q-1個符號的新信源，稱為縮減信源S1；

　　(3)把縮減信源S1的符號仍按概率大小遞減次序排列，再將其最后兩個概率最小的信源符號分別用字符‘O’和‘1’表示，并且合并成一個符號，這樣又形成了q-2個信源符號的縮減信源S2；

　　(4)依次繼續下去，直至信源最后只剩下兩個信源符號為止，將這最后兩個信源符號分別用字符‘O’和‘1’表示；

　　(5)然后從最后一級縮減信源開始，進行回推就得到每種字符所對應的由字符‘O’和‘1’組成的字符串序列，不妨將其稱為偽碼字。

　　這樣，就為需要壓縮的文件建立了一個一一映射f：Si→ci=1，2，…，q。式中：Si代表不同的字符，ci代表對應字符Si的偽碼字。

　　為了將偽碼字變成真正的碼字，又必須建立一個映射g：ci→ω，i=1，2，…，q。式中：ci代表不同的字符，(ωi代表對應字符ci的碼字。該映射g 的功能是將由字符串組成的偽碼字變成二進制數，比如g(010110)=(010110)2=(22)10。從而g[f(Si)]，i=1，2，…，q，就是構造的哈夫曼編碼表。

　　2．3 文件壓縮過程

　　每從文件中讀出一個字符char，用查哈夫曼編碼表的方式得到對應的碼字，然后用這個碼字替換相應的字符g[f(char)]。當文件中的所有字符都經過了碼字替換，則得到一個比原文件要小的壓縮文件。文件之所以能夠被壓縮，是因為每個字符都占8個二進制位的空間。然而，通過碼字替換相應的字符后，有的碼字比相應的字符的碼長要短，有的碼字比相應的字符的碼長要長，但文件在被壓縮后總的長度比原來要短。

　　2．4 文件解壓過程

　　文件的解壓過程是文件的壓縮過程的逆過程，即將一個壓縮文件還原成它的本來面目。因為一個壓縮文件是不能夠直接使用的，只有被解壓后才能使用。一個被壓縮的文件如果不能被解壓，則這種壓縮是毫無意義的。

　　哈夫曼編碼是即時碼，只要得到碼字c，則經查哈夫曼編碼表得到相應字符f-1(g-1(c))，用這個字符替換相應的碼字就是還原的過程。因此，每從壓縮文件中讀出一個碼字，就從哈夫曼編碼表查得相應的字符替換，當文件中所有的碼字被替換掉，這個解壓過程也就完成了。

　　3 高效網絡安全傳輸方法設計

　　一個高效的數據傳輸系統必須保證數據在傳輸中的安全和可靠，包括信息的保密性、完整性，同時在實現數據傳輸中占用更少的資源。所以數據加密傳輸的方案中應包括對發送端數據的有效加密、密鑰的分配、傳輸數據的壓縮。下面主要從信息的壓縮、保密性幾個方面來考慮數據加密傳輸系統中的加密方案。

　　從哈夫曼編碼壓縮的過程可以看出，經過該方法壓縮的數據必須使用壓縮形成的哈夫曼編碼樹才能解壓縮。對于不同的源文件，由于文件內容的不同，形成的哈夫曼編碼樹不同。數據傳輸的過程中需要同時傳輸壓縮數據包和相應的哈夫曼編碼樹結構。相對于壓縮數據包，哈夫曼編碼樹的節點數大大小于數據文件的數據量，如果只對哈夫曼編碼樹進行加密，加密和解密需要處理的數據量將大大減少，對于不對稱加密算法無法處理大量數據的限制也可被克服。在數據傳輸中需要傳輸的數據量比壓縮之前需要傳輸的數據量大大降低，可以節省大量的網絡資源。在大規模的數據安全傳輸中，可以提高數據傳輸的效率和安全性。

　　在信息的保密性方面選擇RSA作為哈夫曼編碼加密傳輸系統中傳輸信息的加密算法，采用公鑰加密來發送哈夫曼編碼。

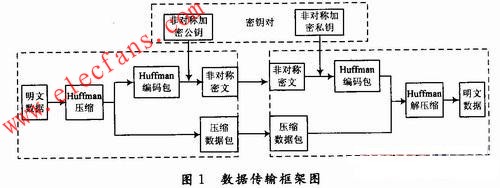
　　具體的數據傳輸實現的框架如圖1所示。

?

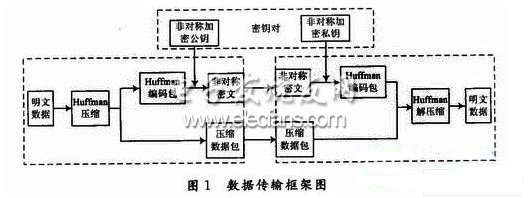
　　安全數據傳輸的各個模塊的功能如下：

　　對需要傳輸的明文數據進行哈夫曼壓縮，壓縮完成后產生哈夫曼編碼樹的代碼集合；用哈夫曼代碼集合對原明文代碼集合進行壓縮轉換；對哈夫曼代碼集合進行RSA算法的公鑰加密；傳輸加密后的哈夫曼代碼集合和壓縮代碼集合；接收端收到數據后，使用私鑰解密哈夫曼

　　代碼集合；使用哈夫曼代碼集合接壓縮形成解壓文件。

　　4 結語

　　在數據安全傳輸過程中，通過對哈夫曼壓縮后的明文數據進行改進的加密，克服了非對稱加密算法加密大數據量文件的缺點，保持了非對稱加密的安全性。通過壓縮減少了數據傳輸的數據量，節省了網絡帶寬的開銷，提高了數據傳輸的效率。這種方法非常適合大量的數據進行互聯網絡安全傳輸。此種方法只有在明文文件中數據的種類及出現的概率都完全相同的極端情況下，數據的傳輸效率才會降到最低。

?

?