隨著智能終端的興起及無線數據應用業務的豐富，無線通信系統中的數據用戶數大幅增加，數據內容也不再限于傳統的文字或者圖像，未來用戶對高清晰度視頻、手機電視等多媒體業務的需求越來越多，導致無線網絡流量呈現出爆炸式增長的態勢。根據市場機構預測，未來10年，無線數據業務將增長500~1000倍，平均每年增長1.6~2倍，這對無線通信系統的網絡容量提出了更高的要求。

　　提升無線通信系統網絡容量的方法有多種，主要包括：提升頻譜效率、提高網絡密度、增加系統帶寬、智能業務分流等。近期研究中，基于大規模天線陣列技術提升頻譜效率的方法獲得越來越多研究人員的關注，是未來移動通信系統中的重要技術。

　　大規模天線陣列系統的基本特征就是通過在基站側配置數量眾多的天線陣列（從幾十至幾千），獲得比傳統天線陣列系統（天線陣列數不超過8個）更為精確的波束控制能力，然后通過空間復用技術，在相同的時頻資源上同時服務更多用戶來提升無線通信系統的頻譜效率，從而滿足未來B4G/5G無線通信系統中海量信息的傳輸需求。另外，大規模天線陣列系統還可以很好地抑制無線通信統中的干擾，帶來巨大的小區內及小區間的干擾抑制增益，使得整個無線通信系統的容量和覆蓋范圍得到進一步提高。

　　然而，在上下行鏈路不存在互異性的無線信道環境下部署大規模天線陣列系統時，遇到的最大問題是下行導頻開銷問題。

　　下行導頻開銷與天線數成正比，而且終端需要向基站反饋下行信道狀態信息，也會帶來比較大的反饋開銷，嚴重影響了大規模天線陣列系統的性能。

　　壓縮感知是在采集信號的時候（模擬到數字），同時完成對信號壓縮之意。由于與壓縮感知有關的嚴密的數學結果或理論剛剛出現，因此壓縮感知是一個相當新的領域，也是近年來極為熱門的研究前沿，在若干應用領域中被廣泛關注。

　　通過分析，無線信道在時域是稀疏的，體現為時延不同、功率不同的多徑，同樣，由于天線之間的信道相關性，經過一定的變換后在變換域上也應該是稀疏的，這就為使用壓縮感知技術來降低導頻開銷提供了可能。

　　本文主要介紹了壓縮感知的技術原理，并分析了其在未來基于大規模天線陣列技術的無線通信系統中的應用。

　　1 技術原理

　　在數字信號處理中，一般都要經過由模擬信號到數字信號的轉換過程，采樣和量化是對信號處理的前提條件。

　　采樣定理是1928年由美國電信工程師奈奎斯特首先提出來的，稱為奈奎斯特采樣定理，該定理指出：要從離散采樣信號中無失真的恢復出原始信號，采樣率要不低于原始信號帶寬的兩倍。該理論幾乎支配著所有信號的獲取、處理、存儲、傳輸等系列過程。

　　D.Donoho、E.Candes及華裔科學家T.Tao等人對信號稀疏和逼近理論進行了大量深入的研究，于2004年初步提出了一種新的信息獲取指導理論：壓縮感知理論。該壓縮感知理論指出：對可壓縮的（稀疏）信號可通過遠低于奈奎斯特采樣速率進行數據采樣后，仍能夠精確地恢復出原始信號。

　　壓縮感知突破了奈奎斯特采樣定理的限制，使得信息理論進入一個新的研究階段，其基本思想是：只要信號是可壓縮的或在某個變換域是稀疏的，那么就可以用一個與變換基不相關的觀測矩陣將變換所得高維信號投影到一個低維空間上，然后通過求解一個最優化問題就可以從這些少量的投影（或稱測量值）中以高概率重構出原信號。

　　在壓縮感知理論的框架下，采樣率不決定于原始信號的帶寬，而取決于重要信息在信號中的結構和內容，測量值并非是信號的本身，而是從高維到低維的投影值，每個測量值都包含了所有樣本信號的少量信息，恢復信號所需測量值的數目遠少于采樣定理要求的數目。

　　對于一個N*1維信號s，其中s中包含K個非零元素，信號s經過公式（1）變換得到N*1維變量x，再經過公式（2）得到M*1維測量信號y，壓縮感知的目的就是通過測量信號y重構出信號s。

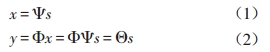
　　其中，Ψ 為N*N 維稀疏變換矩陣，Φ 為M*N 維測量矩陣（也稱為投影矩陣或隨機采樣矩陣），Ψ 、Φ 的設計會嚴重影響壓縮感知技術的性能，K 《M 《N ，M 的取值滿足公式（3）。

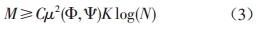
　　其中，μ2（Φ，Ψ）表示矩陣Ψ、Φ的相關性。

　　信號重構是壓縮感知技術的核心，是一個在獲得觀測值y的條件下，尋求最稀疏解s的過程，這里需要引入矩陣理論中的范數概念來描述壓縮感知理論的信號重構問題。

　　定義向量Z={z1，z2，…，zN}的P-范數為：

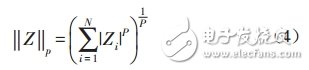
　　當p=0時得到向量Z的0-范數，表示Z中非零元素的個數。

　　通常情況下，對于一個非稀疏的信號x在經過稀疏化變換得到s的情況下，壓縮感知理論中信號恢復問題，轉化為線性約束下的最小0-范數的問題，可以用公式（5）表達：

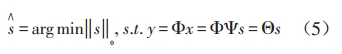
　　對上述0-范數的優化問題，是一個非凸優化問題，也就是在多項式內無法求解，更不能驗證解的有效性，因此需要轉換成其他范數，比如1-范數或2-范數，研究證明對于公式（5）最小0-范數問題可以通過求解一個更加簡單的1-范數最優化問題得到與0-范數同等的解。因此，壓縮感知理論通常用公式（6）描述：

　　針對公式（6）的求解可以用線性規劃算法等最優化理論實現，實際實現時也可以使用其他快速優化算法。

　　2 應用分析

　　壓縮感知應用特征包括：

　　（1）觀測信號不具有稀疏性，例如OFDM系統頻域信道響應或線性陣列響應。

　　（2）通過對觀測信號的基坐標變換，在另外一組基底下，信號變得稀疏，例如頻域信道響應通過DFT變換之后，在時域具有稀疏性。

　　（3）稀疏性（稀疏位置）具有不可知與變化的特性，這是應用壓縮感知的必要條件，如果稀疏位置具有可知性或恒定性。

　　外場測試表明，大部分無線信道在時域上一般都是多徑稀疏的，根據壓縮感知理論，這種稀疏性意味著可以大幅度地降低用戶專有導頻開銷。

　　另外，隨著基站側天線數目增加，無線信道在空域上也同樣體現出稀疏性，這意味著通過壓縮感知技術可以有效減少小區公有導頻的開銷。

　　2.1 用戶專有導頻設計

　　根據壓縮感知理論，再根據公式（6）可知，具有稀疏性的時域無線信道系數可以由在頻域中少量分布的導頻觀測信號通過壓縮感知技術恢復出來。

　　在未來移動通信系統的用戶專有導頻設計中，基于壓縮感知技術，需要考慮的問題有：

　　（1）導頻數目：估計信道的稀疏度K，然后利用公式（3）大概算一下需要的導頻符號的數目m。

　　（2）導頻位置：由測量矩陣決定，設計時一定要保證其隨機性，可以根據小區標識、幀號、子幀號、資源位置作為隨機矩陣生成因子，獲取足夠稀疏的導頻位置，或者在標準化時預定義若干組隨機導頻位置，調度時根據系統參數確定使用哪一組隨機導頻位置，這與現有的LTE系統是明顯不同的，現有系統中導頻是均勻分布的，其間隔主要考慮了相關帶寬。

　　（3）變換矩陣：優先考慮離散傅里葉變換矩陣。

　　（4）信號重構：接收方按照圖1所示的流程，利用少量的頻域導頻信道值y，恢復時域信道h，其中目標函數最優化可以使用實現復雜度較低的Stomp算法。

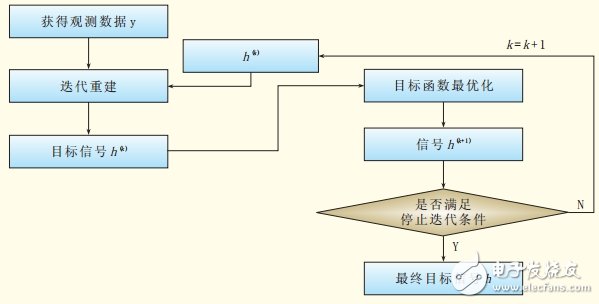
　　圖1 壓縮感知技術的信號重構流程

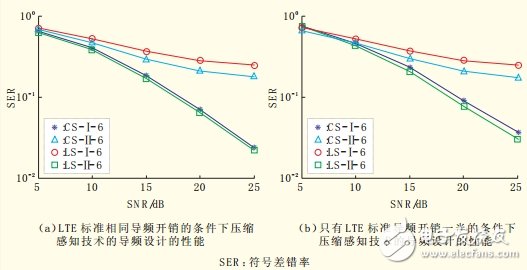
　　圖2 基于壓縮感知技術導頻設計仿真性能

　　圖2給出了基于壓縮感知技術進行用戶專有導頻設計后與傳統的LTE導頻相比的性能，圖2為在擴展城市環境信道模型（ETU）場景、10MHz、16QAM下的符號差錯率（SER）比較，其中LS-Ⅰ-6代表LTE標準導頻模式，時域不做基于CP的截斷處理，子載波間隔為6的仿真參數設置下的仿真結果；LS-Π-6代表LTE標準導頻模式，時域做基于CP的截斷處理，子載波間隔為6的仿真參數設置下的仿真結果；CS-Ⅰ-6代表壓縮感知導頻模式，時域不做基于CP的截斷處理，子載波開銷與LTE導頻開銷相同的仿真參數設置下的仿真結果；CS-Π-6代表壓縮感知導頻模式，時域做基于CP的截斷處理，子載波開銷與LTE導頻開銷相同的仿真參數設置下的仿真結果；CS-Ⅰ-12代表壓縮感知導頻模式，時域不做基于CP的截斷處理，子載波開銷是LTE導頻開銷一半的仿真參數設置下的仿真結果；CS-Π-12代表壓縮感知導頻模式，時域做基于CP的截斷處理，子載波開銷是LTE導頻開銷一半的仿真參數設置下的仿真結果。圖2（a）給出了在LTE標準相同導頻開銷的條件下壓縮感知技術的導頻設計的性能，圖2（b）給出了在只有LTE標準導頻開銷一半的條件下壓縮感知技術的導頻設計的性能。從仿真結果可以看出，基于壓縮感知技術設計的導頻可以有效降低系統開銷，并提升接收方的解碼能力。

　　2.2 小區公有導頻設計

　　在大規模天線陣列系統中，基站側天線數目增加，帶來了小區公有導頻開銷的增加，會嚴重影響未來移動通信系統的性能，因此尋求一種基于低導頻密度的信道估計方法變得非常必要。

　　隨著基站側天線數目增加，信道在空域上是否存在稀疏性是需要首先驗證的問題。

　　圖3給出了對基站配置128根天線形成的瞬時信道進行離散傅立葉變換（DFT）后得到的角度域功率譜分布情況，可以看出，變換后得到的變量是具有稀疏性的，因此可以通過壓縮感知技術設計未來移動通信系統中的小區公有導頻。

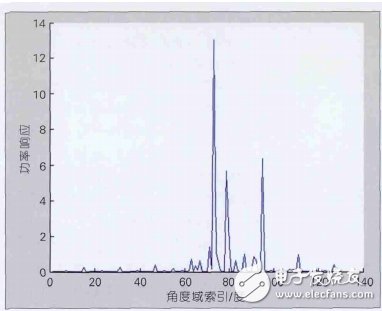
　　圖3 128根天線信道的角度域功率譜分布

　　小區間公有導頻設計導頻數目、導頻位置、信號重構可參考用戶專有導頻設計的思路，變換矩陣設計有兩種方式：

　　式中Ψ是DFT矩陣。

　　基于方式1和方式2進行小區間公有導頻設計的仿真結果如圖4所示。圖4為累計分布函數，不考慮干擾/噪聲。

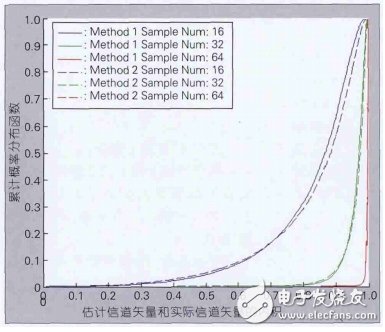
　　圖4 不同變換矩陣空域壓縮感知性能分析

　　可以看出，兩種方式都可以比較好地通過壓縮感知技術重建空域信道，當隨機采樣點數目比較多時，兩種變換矩陣重建信道時性能差別不大，但是當隨機采樣點數比較少時，方式2可以更好地重建信道，主要原因在于方式2提供的變換矩陣更好地體現了天線之間的相關性。

　　3 結束語

　　通過理論分析及大量仿真，證明了壓縮感知技術可以有效地降低系統導頻開銷，提升系統性能。

　　后續也可以考慮將壓縮感知技術與未來移動通信系統中可能使用的認知無線電技術結合起來用于發現空閑頻譜比較多的頻段內的空閑資源，有效降低系統硬件實現成本，或者是將壓縮感知技術與其他天線降維技術結合起來，提升未來移動通信系統的用戶體驗。