摘要：差分跳頻是一種數字通信系統，其頻率跳變速度快，通信保密性好。接收機采用軟件無線電的技術解調。解調窗口的同步是關鍵技術，是正確解調的前提。推導出同步算法的計算公式，給出相應的數據圖表和流程圖。該算法同步建立時間短，運算量小，并且可以實時調整，在仿真中取得成功。

1 差分跳頻簡介

差分跳頻系統工作于短波波段（2MHz～30MHz），頻率跳變速度5000跳/s，最高數據傳輸速度為19.2kbps。5000跳/s的頻率跳變使得頻率不易被跟蹤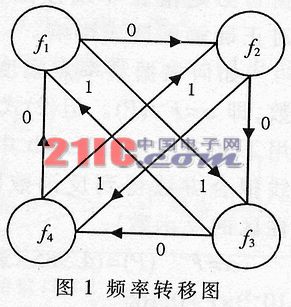，通信保密性好。差分跳頻不同于傳統的模擬跳頻，發射機采用DDS直接合成發送頻率，接收機采用軟件無線電方法解調。

簡單說明系統的工作方式，見圖1頻率轉移圖。系統待發數據為0110110……。當第一個bit'0'到來時，頻率點由f1轉移到f2，該bit'0'用頻率f2發送；當第二個bit'1'到來時，頻率點由f2轉移到f4，以此類推解調時，將接收信號采樣的數字信號，對采樣數據進行快速傅立葉變換（FFT）運算，識別當前的頻率點，然后保護頻率轉移圖和前一次的頻率點解調原始數據。

實際系統的參數如下：將2.56MHz～28.16MHz的頻帶等間隔劃分為10個信道，每個信道以5kHz等間隔取256頻率點。通信開始前，系統掃描10信道，動態決定一個特性最好的信道用來通信，收發雙方按協議從選定信道的256個頻率點中取64作為工作頻率，按存儲在系統中的頻率轉移圖進行通信。該系統支持三種數據傳輸速率：4.8kbps、9.6kbps和19.6kbps。

2 同步策略

差分跳頻系統采用軟件無線電的方法進行數據解調。軟件無線電結構降低了系統硬件的復雜性，接收機不需要傳統模擬跳頻系統中的頻率合成電路和硬件的同步電路。但沒有硬件的同步電路后，采用何種軟件算法快速實現同步成為關鍵技術之一。

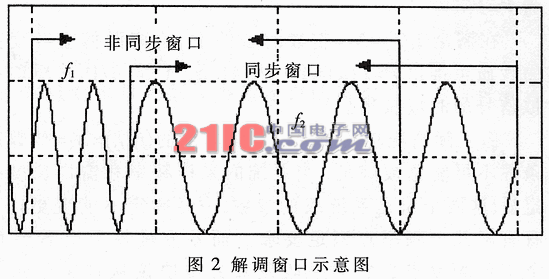
    如圖2所示，接收信號經過A/D采樣變為數字信號，然后對一跳時間內（以下稱為解調窗口）的采樣數據進行FFT運算，識別當前的頻率點，依據頻率轉移圖和前一次的頻率點解調原始數據。如果解調窗口不同步，則窗口內會出現兩個頻率點，無法判定該用哪個工作為解調頻率點。因此必須將不同步的解調窗口滑動到同步位置，才能正確解調數據。

筆者設計的同步方法簡述如下：

（1）隨機選擇初始窗口，對采樣數據作FFT運算，識別可能出現的兩個頻率點f1和f2以及FFT后的相應幅度P1和P2（在頻域中頻率點的能量與幅度的平方成正比，為簡化以幅度代替能量計算）。

（2）判斷這兩個頻率點在時域波形上的順序。

    （3）頻率點f的幅度P（請注意，這里指FFT后的頻域幅度）只與兩個因素有關：采樣前模擬信號的時域振幅和該頻率點在解調窗口內點據的時間長度。模擬信號的時域振幅可以在接收端采用自動增益控制保持常數值。那么，P只要頻率點在解調窗口內點據時間長度（也就是該頻率點占據的采樣點數目）的單值函數，只要找到這個函數，即可先由FFT計算出幅度P，反求該頻率點占據的窗口長度，最后將窗口滑動適當長度即可同步。

以下假設：采樣頻率為fs,解調窗口總長度為N，某一頻率點占據的長度為N1。

定義：α=N1/N

3 實現的方式

具體實現要考慮很多復雜的情況，詳細說明如下。

首先要找到（3）中提及的函數關系，這個函數關系記為P=F(α)。

在滿足（f1/fs）×N1=整數的條件下，由離散傅立葉變換的性質可推出P=F（α）=A·（N/4）·α，A是A/D采樣前模擬信號的時域振幅。

但實際情況更為復雜。上面提到的（f1fs）×N1=整數的條件不可能總被滿足。當系統的采樣頻率和窗口長度確定后（這兩個量是系統級的參數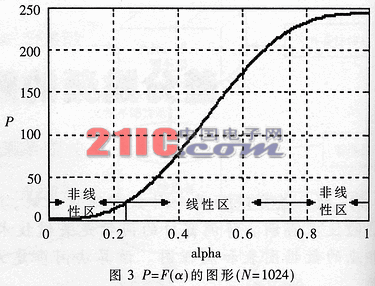，一經確定不能變更），只有有限幾個頻率點滿足要求。而差分跳頻系統需要64個工作頻率點，它們是收發雙方按協議從選定信道的512個頻率點中選擇的，也就是說512個頻點都有可能成為工作頻率點，絕大部分不滿足工作。如果條件得不到滿足，那么公式修改為P=F（α）=H（f, α）·A·(N/4)·α。因子H（f,α）依賴于頻率和α。H（f,α）無法動態自適應計算，因為依賴于α，而α恰好是要求解的變量。因此，直接對采樣數據進行計算的方法不太可取。

還有一點，希望該跳頻系統降低對同步的敏感性，從而降低復雜性和運算量，因此希望P=F（α）是非線性函數，以改善系統特性。

可采用對采樣數據預先加窗函數修正的方法。本系統采用海明窗，因為海明窗是滿足要求的最簡單窗函數，并且可以理論推導出P=F(α)的函數式。海明窗定義為：

W（n）=0.5+0.5cos[2(π-N/2)] n=0,1,2,…，N-1 （1）

經過推導得到加窗后的P=F（α）的估計式為：

P=F（α）=0.935A·N·{α/4-sin(2πα)/(8π)+[cos(α)-1]/(8π)} (2)

圖3是用Matlab仿真得出的P=F（α）的圖形。該圖形不是按（2）式直接繪制的，它是實際仿真得到的結果，與（2）式彼此獨立，但（2）式的圖形也基本是這個圖形。（2）式中的系數0.93可以在（0.92～0.94）之間微調。

圖3是Matlab按下述方法計算得到的：對應每一個α值，在滿足采樣定理前提下隨機選擇1000點頻率，讓其占據的窗口相對長度為α，計算FFT后的頻域幅度，求1000點的平均值作為縱坐標。因此圖3所表達的函數不依賴于具體頻率。這個圖劃分為線性區和非線性區，線性區的范圍為0.25<α<0.75。解調窗口進入非線性區的意思是窗口位置距離同步位置非常近了，再經過細致調整就可以同步。

圖3整體上是非線性函數，非線性的好處是降低了系統對同步的敏感性。假設解調窗口稍微不同步，那么窗口必定落在非線性區，在該區幅度變化不顯著，不會對正確解調造成影響。

    如果根據頻率點幅度P求α？先求解P=F(α)的反函數，即α=F-1（P）。但（2）式求不出閉合解析的反函數。可用下述方法：在Matlab中繪制圖3的反函數，再使用曲線擬合方法得到反函數的表達式（公式（3）只適用于線性區的反函數）：

α=F-1（P）=（4.985×10-8）×P3-(1.8×10-5) ×P2+(4.131×10-3) ×P+0.166

第二個復雜的情況是必須判斷解調窗口類型。

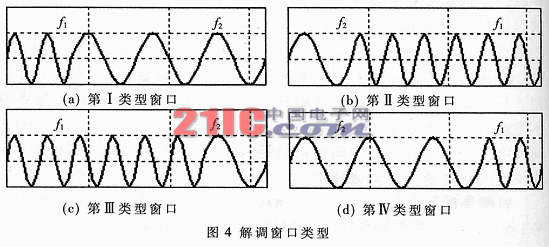
假設初始的解調窗口未同步，則該窗口內有兩個頻率點f1和f2，依據這兩個頻率的時域順序和所占據的窗口長度（也就是域中兩個頻率的幅度）有四種情況，分別稱為第I、第II、第III、第IV類型窗口，見圖4。每個窗口都假定不同步，且只繪出一跳時間內的波形。

為什么要判定窗口類型呢？因為實際計算時取幅度較大的頻率點來求解α，這樣可降低噪聲的干擾。但幅度較大的頻率點可能是f1也可能是f2，在時域中的順序可能在前也可能在后，于是形式四種類型。

如果初始窗口進入非線性區，因非線性區頻率點幅度變化小，為降低噪聲影響，在非線性區移動的點就是固定值（這個值可以根據實際需要加以微調）。判斷窗口是否進入非線性區的準則為：是否有一個頻點的幅度超過門限值。

圖5

4 流程

經過以上討論，得出實際的算法流程見圖5。

說明：如果第一次滑動窗口后未能進入預定同步位置，則繼續第二次調整。此時移動后的窗口以大概率進入大非線性區，如果第二次滑動窗口仍舊不同步，則繼續第三次調整，至多三次調整后，以95%概率進入同步鎖定。三次調整后仍不同步（至多5%概率），判定為同步失敗，選擇窗口重新計算。

以上的窗口是向右滑動的（也就是向時間軸正向滑動），如果系統開辟較大緩沖區，也可以向左滑動（也就是向時間軸負向滑動），此時前面的數據不能丟失，并且對第III和第IV類型窗口的滑動點數變為絕對值較小的負數值。

該同步算法的優點是同步建立時間短，運算量小，可以實時調整。對接收數據加窗函數修正降低了系統對同步的敏感性。該算法在系統仿真中取得成功。