阻抗匹配與史密斯(Smith)圓圖: 基本原理 |
| 本文利用史密斯圓圖作為RF阻抗匹配的設計指南。文中給出了反射系數、阻抗和導納的作圖范例,并用作圖法設計了一個頻率為60MHz的匹配網絡。 實踐證明:史密斯圓圖仍然是計算傳輸線阻抗的基本工具。 在處理RF系統的實際應用問題時,總會遇到一些非常困難的工作,對各部分級聯電路的不同阻抗進行匹配就是其中之一。一般情況下,需要進行匹配的電路包括天線與低噪聲放大器(LNA)之間的匹配、功率放大器輸出(RFOUT)與天線之間的匹配、LNA/VCO輸出與混頻器輸入之間的匹配。匹配的目的是為了保證信號或能量有效地從“信號源”傳送到“負載”。 在高頻端,寄生元件(比如連線上的電感、板層之間的電容和導體的電阻)對匹配網絡具有明顯的、不可預知的影響。頻率在數十兆赫茲以上時,理論計算和仿真已經遠遠不能滿足要求,為了得到適當的最終結果,還必須考慮在實驗室中進行的RF測試、并進行適當調諧。需要用計算值確定電路的結構類型和相應的目標元件值。 有很多種阻抗匹配的方法,包括:
本文的主要目的是復習史密斯圓圖的結構和背景知識,并且總結它在實際中的應用方法。討論的主題包括參數的實際范例,比如找出匹配網絡元件的數值。當然,史密斯圓圖不僅能夠為我們找出最大功率傳輸的匹配網絡,還能幫助設計者優化噪聲系數,確定品質因數的影響以及進行穩定性分析。
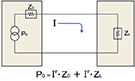
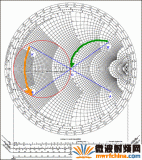
圖1. 阻抗和史密斯圓圖基礎 基礎知識 在介紹史密斯圓圖的使用之前,最好回顧一下RF環境下(大于100MHz) IC連線的電磁波傳播現象。這對RS-485傳輸線、PA和天線之間的連接、LNA和下變頻器/混頻器之間的連接等應用都是有效的。 大家都知道,要使信號源傳送到負載的功率最大,信號源阻抗必須等于負載的共軛阻抗,即:
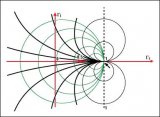
圖2. 表達式Rs + jXs = RL - jXL的等效圖 在這個條件下,從信號源到負載傳輸的能量最大。另外,為有效傳輸功率,滿足這個條件可以避免能量從負載反射到信號源,尤其是在諸如視頻傳輸、RF或微波網絡的高頻應用環境更是如此。 史密斯圓圖 史密斯圓圖是由很多圓周交織在一起的一個圖。正確的使用它,可以在不作任何計算的前提下得到一個表面上看非常復雜的系統的匹配阻抗,唯一需要作的就是沿著圓周線讀取并跟蹤數據。 史密斯圓圖是反射系數(伽馬,以符號表示)的極座標圖。反射系數也可以從數學上定義為單端口散射參數,即s11。 史密斯圓圖是通過驗證阻抗匹配的負載產生的。這里我們不直接考慮阻抗,而是用反射系數L,反射系數可以反映負載的特性(如導納、增益、跨導),在處理RF頻率的問題時,L更加有用。 我們知道反射系數定義為反射波電壓與入射波電壓之比:
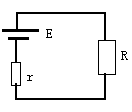
圖3. 負載阻抗 負載反射信號的強度取決于信號源阻抗與負載阻抗的失配程度。反射系數的表達式定義為: 由于阻抗是復數,反射系數也是復數。 為了減少未知參數的數量,可以固化一個經常出現并且在應用中經常使用的參數。這里Zo (特性阻抗)通常為常數并且是實數,是常用的歸一化標準值,如50、75、100和600。于是我們可以定義歸一化的負載阻抗: 據此,將反射系數的公式重新寫為: 從上式我們可以看到負載阻抗與其反射系數間的直接關系。但是這個關系式是一個復數,所以并不實用。我們可以把史密斯圓圖當作上述方程的圖形表示。 為了建立圓圖,方程必需重新整理以符合標準幾何圖形的形式(如圓或射線)。 首先,由方程2.3求解出; 并且 令等式2.5的實部和虛部相等,得到兩個獨立的關系式: 重新整理等式2.6,經過等式2.8至2.13得到最終的方程2.14。這個方程是在復平面(r, i)上、圓的參數方程(x-a)2 + (y-b)2 = R2,它以(r/r+1, 0)為圓心,半徑為1/1+r. 更多細節參見圖4a。
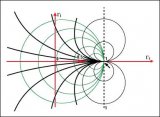
圖4a. 圓周上的點表示具有相同實部的阻抗。例如,R=1的圓,以(0.5, 0)為圓心,半徑為0.5。它包含了代表反射零點的原點(0, 0) (負載與特性阻抗相匹配)。以(0,0)為圓心、半徑為1的圓代表負載短路。負載開路時,圓退化為一個點(以1,0為圓心,半徑為零)。與此對應的是最大的反射系數1,即所有的入射波都被反射回來。 在作史密斯圓圖時,有一些需要注意的問題。下面是最重要的幾個方面:
作圖 經過等式2.15至2.18的變換,2.7式可以推導出另一個參數方程,方程2.19。 同樣,2.19也是在復平面(r, i)上的圓的參數方程(x-a)2 + (y-b)2 = R2,它的圓心為(1, 1/x),半徑1/x。 更多細節參見圖4b。
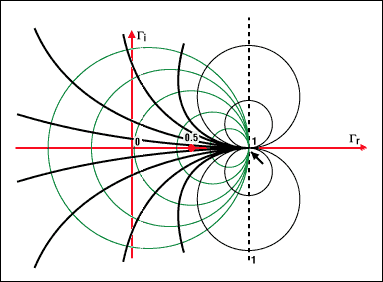
圖4b. 圓周上的點表示具有相同虛部x的阻抗。例如,x=1的圓以(1, 1)為圓心,半徑為1。所有的圓(x為常數)都包括點(1, 0)。與實部圓周不同的是,x既可以是正數也可以是負數。這說明復平面下半部是其上半部的鏡像。所有圓的圓心都在一條經過橫軸上1點的垂直線上。 完成圓圖 為了完成史密斯圓圖,我們將兩簇圓周放在一起。可以發現一簇圓周的所有圓會與另一簇圓周的所有圓相交。若已知阻抗為r + jx,只需要找到對應于r和x的兩個圓周的交點就可以得到相應的反射系數。 可互換性 上述過程是可逆的,如果已知反射系數,可以找到兩個圓周的交點從而讀取相應的r和x的值。過程如下:
推論 因為史密斯圓圖是一種基于圖形的解法,所得結果的精確度直接依賴于圖形的精度。下面是一個用史密斯圓圖表示的RF應用實例: 例: 已知特性阻抗為50,負載阻抗如下:
對上面的值進行歸一化并標示在圓圖中(見圖5):
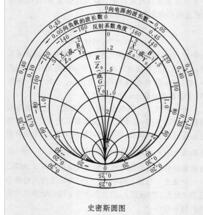
圖5. 史密斯圓圖上的點 現在可以通過圖5的圓圖直接解出反射系數。畫出阻抗點(等阻抗圓和等電抗圓的交點),只要讀出它們在直角坐標水平軸和垂直軸上的投影,就得到了反射系數的實部r和虛部i (見圖6)。 該范例中可能存在八種情況,在圖6所示史密斯圓圖上可以直接得到對應的反射系數:
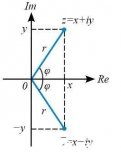
圖6. 從X-Y軸直接讀出反射系數的實部和虛部 用導納表示 史密斯圓圖是用阻抗(電阻和電抗)建立的。一旦作出了史密斯圓圖,就可以用它分析串聯和并聯情況下的參數。可以添加新的串聯元件,確定新增元件的影響只需沿著圓周移動到它們相應的數值即可。然而,增加并聯元件時分析過程就不是這么簡單了,需要考慮其它的參數。通常,利用導納更容易處理并聯元件。 我們知道,根據定義Y = 1/Z,Z = 1/Y。導納的單位是姆歐或者-1 (早些時候導納的單位是西門子或S)。并且,如果Z是復數,則Y也一定是復數。 所以Y = G + jB (2.20),其中G叫作元件的“電導”,B稱“電納”。在演算的時候應該小心謹慎,按照似乎合乎邏輯的假設,可以得出:G = 1/R及B = 1/X,然而實際情況并非如此,這樣計算會導致結果錯誤。 用導納表示時,第一件要做的事是歸一化, y = Y/Yo,得出 y = g + jb。但是如何計算反射系數呢?通過下面的式子進行推導: 結果是G的表達式符號與z相反,并有(y) = -(z). 如果知道z,就能通過將的符號取反找到一個與(0,0)的距離相等但在反方向的點。圍繞原點旋轉180°可以得到同樣的結果。(見圖7).
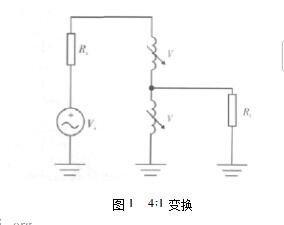
圖7. 180°度旋轉后的結果 當然,表面上看新的點好像是一個不同的阻抗,實際上Z和1/Z表示的是同一個元件。(在史密斯圓圖上,不同的值對應不同的點并具有不同的反射系數,依次類推)出現這種情況的原因是我們的圖形本身是一個阻抗圖,而新的點代表的是一個導納。因此在圓圖上讀出的數值單位是姆歐。 盡管用這種方法就可以進行轉換,但是在解決很多并聯元件電路的問題時仍不適用。 導納圓圖 在前面的討論中,我們看到阻抗圓圖上的每一個點都可以通過以復平面原點為中心旋轉180°后得到與之對應的導納點。于是,將整個阻抗圓圖旋轉180°就得到了導納圓圖。這種方法十分方便,它使我們不用建立一個新圖。所有圓周的交點(等電導圓和等電納圓)自然出現在點(-1, 0)。使用導納圓圖,使得添加并聯元件變得很容易。在數學上,導納圓圖由下面的公式構造: 解這個方程 接下來,令方程3.3的實部和虛部相等,我們得到兩個新的獨立的關系: 從等式3.4,我們可以推導出下面的式子: 它也是復平面 (r, i)上圓的參數方程(x-a)2 + (y-b)2 = R2 (方程3.12),以(-g/g+1, 0)為圓心,半徑為1/(1+g)。 從等式3.5,我們可以推導出下面的式子: 同樣得到(x-a)2 + (y-b)2 = R2型的參數方程(方程3.17)。 求解等效阻抗 當解決同時存在串聯和并聯元件的混合電路時,可以使用同一個史密斯圓圖,在需要進行從z到y或從y到z的轉換時將圖形旋轉。 考慮圖8所示網絡(其中的元件以Zo=50進行了歸一化)。串聯電抗(x)對電感元件而言為正數,對電容元件而言為負數。而電納(b)對電容元件而言為正數,對電感元件而言為負數。 圖8. 一個多元件電路 這個電路需要進行簡化(見圖9)。從最右邊開始,有一個電阻和一個電感,數值都是1,我們可以在r=1的圓周和I=1的圓周的交點處得到一個串聯等效點,即點A。下一個元件是并聯元件,我們轉到導納圓圖(將整個平面旋轉180°),此時需要將前面的那個點變成導納,記為A'。現在我們將平面旋轉180°,于是我們在導納模式下加入并聯元件,沿著電導圓逆時針方向(負值)移動距離0.3,得到點B。然后又是一個串聯元件。現在我們再回到阻抗圓圖。 圖9. 將圖8網絡中的元件拆開進行分析 在返回阻抗圓圖之前,還必需把剛才的點轉換成阻抗(此前是導納),變換之后得到的點記為B',用上述方法,將圓圖旋轉180°回到阻抗模式。沿著電阻圓周移動距離1.4得到點C就增加了一個串聯元件,注意是逆時針移動(負值)。進行同樣的操作可增加下一個元件(進行平面旋轉變換到導納),沿著等電導圓順時針方向(因為是正值)移動指定的距離(1.1)。這個點記為D。最后,我們回到阻抗模式增加最后一個元件(串聯電感)。于是我們得到所需的值,z,位于0.2電阻圓和0.5電抗圓的交點。至此,得出z=0.2 + j0.5。如果系統的特性阻抗是50,有 Z = 10 + j25 (見圖10)。 圖10. 在史密斯圓圖上畫出的網絡元件 逐步進行阻抗匹配 史密斯圓圖的另一個用處是進行阻抗匹配。這和找出一個已知網絡的等效阻抗是相反的過程。此時,兩端(通常是信號源和負載)阻抗是固定的,如圖12所示。我們的目標是在兩者之間插入一個設計好的網絡已達到合適的阻抗匹配。
圖11. 阻抗已知而元件未知的典型電路 初看起來好像并不比找到等效阻抗復雜。但是問題在于有無限種元件的組合都可以使匹配網絡具有類似的效果,而且還需考慮其它因素(比如濾波器的結構類型、品質因數和有限的可選元件)。 實現這一目標的方法是在史密斯圓圖上不斷增加串聯和并聯元件、直到得到我們想要的阻抗。從圖形上看,就是找到一條途徑來連接史密斯圓圖上的點。同樣,說明這種方法的最好辦法是給出一個實例。 我們的目標是在60MHz工作頻率下匹配源阻抗(ZS)和負載阻抗(ZL) (見圖12)。網絡結構已經確定為低通,L型(也可以把問題看作是如何使負載轉變成數值等于ZS的阻抗,即ZS復共軛)。下面是解的過程: 圖12. 圖11的網絡,將其對應的點畫在史密斯圓圖上 要做的第一件事是將各阻抗值歸一化。如果沒有給出特性阻抗,選擇一個與負載/信號源的數值在同一量級的阻抗值。假設 Zo為50。于是 zS = 0.5 -j0.3, z*S = 0.5 + j0.3, ZL = 2 -j0.5。 下一步,在圖上標出這兩個點,A代表zL,D代表Z*S 然后判別與負載連接的第一個元件(并聯電容),先把zL轉化為導納,得到點A'。 確定連接電容C后下一個點出現在圓弧上的位置。由于不知道C的值,所以我們不知道具體的位置,然而我們確實知道移動的方向。并聯的電容應該在導納圓圖上沿順時針方向移動、直到找到對應的數值,得到點B (導納)。下一個元件是串聯元件,所以必需把B轉換到阻抗平面上去,得到B'。B'必需和D位于同一個電阻圓上。從圖形上看,從A'到D只有一條路徑,但是如果要經過中間的B點(也就是B'),就需要經過多次的嘗試和檢驗。在找到點B和B'后,我們就能夠測量A'到B和B'到D的弧長,前者就是C的歸一化電納值,后者為L的歸一化電抗值。A'到B的弧長為b = 0.78,則B = 0.78 x Yo = 0.0156姆歐。因為C = B,所以 C = B/ = B/(2 f) = 0.0156/(2 607) = 41.4pF。B到D的弧長為 x = 1.2,于是 X = 1.2 × Zo = 60.由L = X, 得 L = X/ = X/(2 f) = 60/(2 607) = 159nH。 總結 在擁有功能強大的軟件和高速、高性能計算機的今天,人們會懷疑在解決電路基本問題的時候是否還需要這樣一種基礎和初級的方法。 實際上,一個真正的工程師不僅應該擁有理論知識,更應該具有利用各種資源解決問題的能力。在程序中加入幾個數字然后得出結果的確是件容易的事情,當問題的解十分復雜、并且不唯一時,讓計算機作這樣的工作尤其方便。然而,如果能夠理解計算機的工作平臺所使用的基本理論和原理,知道它們的由來,這樣的工程師或設計者就能夠成為更加全面和值得信賴的專家,得到的結果也更加可靠。
本文的相似版本發表在2000年7月的RF Design上。 |
 電子發燒友App
電子發燒友App









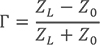














評論