虞卞雨萱 1,陸科林 1 ,符啟恩 1,張寧 2
(1. 東南大學自動化學院,南京 210096; 2. 北京機電工程研究所,北京 100074)
【引用格式】虞卞雨萱,陸科林,符啟恩,等。 基于神經網絡和無跡卡爾曼濾波融合的天線罩誤差斜率估計方法[J]。戰術導彈技術,2023(1):121-131.
DOI:10.16358/j.issn.1009-1300.20220183
摘 要為消除導引頭天線罩引入的瞄準誤差對制導系統穩定性和精度造成的負面影響,提出了一種基于神經網絡和無跡卡爾曼濾波融合的天線罩誤差斜率估計方法。考慮先驗模型知識,分別建立導引頭、自動駕駛儀、彈目相對運動系統和彈體動力學系統的動態模型,選取真實視線角、視角和天線罩誤差斜率作為狀態變量,根據視線角觀測值建立測量模型。考慮到模型的不確定性,基于神經網絡技術學習非線性濾波模型中的動力學方程,結合無跡卡爾曼濾波技術,根據所學習的代理模型和帶噪聲的系統量測,對天線罩誤差斜率等狀態進行實時在線估計。與傳統采用非線性濾波技術的天線罩誤差斜率估計方法相比,本方法基于數據驅動思想,減少了對精確動力學模型的依賴,能有效消除模型不確定性的影響。與單純采用離線訓練構造的神經網絡相比,本方法結合貝葉斯濾波理論,對實時數據具有更強的適應性。經多次仿真實驗,證實該方法能夠有效控制預測誤差,具有較高精度。
1 引 言
現代戰爭中,出于人道主義和有效打擊的考量,精準的點目標打擊逐漸取代了大面積轟炸,如何實現精確制導成為各國學者關注的重點。雷達尋的導彈是精確制導武器的代表之一,它利用雷達導引頭獲得目標的角度觀測,并結合制導律實現目標跟蹤,進而精確打擊,這個角度觀測即為視線角(Line of Sight Angle,LOS)。 出于流線型的外形需求和防止氣流擾動影響天線測量結果的考慮,雷達導引頭并非直接暴露在導彈頭部,而是罩有一個保護裝置:導引頭天線罩(Antenna Radome)[1]。但是天線罩會影響電磁波的傳輸[2],使電磁信號發生衰減、折射和反射等效應,從而造成瞄準線誤差,形成天線罩誤差角,這種測量誤差將降低有效導航比,增大脫靶量[3]。更嚴重的是,這使得彈體姿態耦合到導引頭,在制導回路內部形成一條寄生回路,嚴重影響制導系統的穩定性[4],加大了控制難度。
為避免天線罩誤差帶來的負面影響,最直接的思路是對天線罩進行精確建模,文獻[5]根據電磁波折射理論推導了波束指向偏移模型,創新地結合了相控陣天線陣列測角原理,成功定位了有天線罩時檢測角所對應的最大波束指向角度,提升了檢測角誤差的準確性,將誤差從1°降低到0.1°以下。 另一種思路是獲取天線罩誤差斜率估計,從而對天線罩誤差進行補償。常見的估計方法有傳統的非線性濾波估計、多模型算法和機器學習等。傳統的非線性濾波是對經典的線性卡爾曼濾波(Kalman Filter,KF)的非線性變種,常見的有擴展卡爾曼濾波(Extended Kalman Filter,EKF)、無跡卡爾曼濾波(Unscented Kalman Filter,UKF)等。
文獻[6]利用擴展卡爾曼濾波方法,結合彈目相對運動和導引頭模型建立非線性濾波器,對天線罩斜率進行估計并用于補償,顯著改善了導彈的穩定性和制導精度。文獻[7]則在此基礎上進行了三維模型下的濾波設計:縱側向通道聯合估計視線角速率和天線罩誤差斜率的擴展卡爾曼濾波器,進一步提高了天線罩誤差影響下的制導精度。文獻[8]提出了一種基于無跡卡爾曼濾波的隔離度在線補償方法,首先建立了包含天線罩誤差的雷達導引頭隔離度模型,運用該補償方法,在速度指向誤差和目標常值機動輸入下均能估計出天線罩誤差斜率,從而改善了制導性能,提高了制導精度。
文獻[9]基于擴展卡爾曼濾波的方法通過建立雷達導引頭的寄生環模型,實現實時補償,提升導彈的穩定性和制導精度,但是該方法也僅適用于能夠精確建模的情況。 利用多模型算法估計天線罩斜率的思路最早是由Yueh在文獻[10]中提出,其后有許多學者對該方法進行了進一步研究。例如,金鵬飛在文獻[11]中采用模型參考自適應算法對天線罩誤差斜率進行在線估計,并針對算法中的參數選擇問題,提出了改進的參數自適應調節律,實現了對天線罩誤差斜率準確且快速的估計。
利用機器學習技術估計天線罩誤差,文獻[12]利用歷史數據訓練神經網絡,實現了離線補償。文獻[13]提出了一種基于機器學習和修正物理光學方法的天線罩雷達截面計算方法。利用多層感知器(Multilayer Perceptron, MLP)模型估計了天線隨機系統的散射機理,用函數擬合估計FSS層的頻率響應與入射角、偏振度和頻率的關系,從而提高了天線罩表面電流計算的精度,但是該方法完全依賴于歷史模式,缺乏對實時數據的適應性。 除此之外,考慮到傳統非線性濾波對模型精確性的高要求和機器學習對訓練集外、實際情況中不可預測噪聲的適應性問題,近年來,傳統濾波與機器學習相結合的估計方法也被廣泛關注。文獻[14]提出一種基于粒子濾波(Particle Filter, PF)與長短期記憶網絡(Long Short Term Memory Network,LSTM)融合的在線預測方法。粒子濾波方法需要精確的狀態模型,而精確的轉移方程往往難以得到,文獻[14]利用歷史數據訓練LSTM模型作為PF的狀態轉移方程,從而解決了PF的經驗方程依賴問題,同時PF還能給出不確定性表達。研究結果表明,該方法模型更新簡單有效,預測精度好。
學習數據構建神經網絡模型并配合序貫濾波器進行估計,這一方法在很多其他學科中廣泛應用,如文獻[15]融合長短期記憶神經網絡與卡爾曼濾波,提出了一種混合模型KF-LSTM,其結果優于LSTM模型和KF模型單獨使用的結果;文獻[16]中用多層前饋神經網絡(Feedforward Neural Network,FNN)對測量建模,再通過卡爾曼濾波器進行估計,其結果更接近真實值;文獻[17]提出一種基于高階容積卡爾曼濾波(High Order Cubature Kalman Filter,HCKF)和神經網絡的狀態估計算法,利用前饋神經網絡建立狀態空間模型,然后采用HCKF對新狀態進行更新,從而實現對狀態值的精確估計。為了使狀態方程更好地預測狀態變量的走向,文獻[18]利用循環神經網絡(Recurrent Neural Network,RNN)學習歷史數據,對狀態進行建模,在此基礎上,利用集合卡爾曼濾波(Ensemble Kalman Filtering)進行反演,得到的結果更為精確,實現聲速剖面波動的追蹤。
綜上所述,只應用傳統非線性濾波技術進行估計的方法(如文獻[6-9]),可以根據系統觀測適應實時情況,但其估計精度完全依賴于動力學模型的準確性,僅適用于能夠精確建模的情況。而僅使用離線訓練構造的神經網絡的估計方法(如文獻[12-13]),從歷史數據中學習模式,缺乏對實時數據的適應性。故本文參考文獻[14-18]的思想,綜合傳統非線性濾波技術和神經網絡的優點,提出一種基于神經網絡和無跡卡爾曼濾波的估計方法。 本文針對二維彈目相對運動模型中存在狀態方程部分未知的情況,提出利用神經網絡學習歷史數據建立狀態轉移方程,再結合無跡卡爾曼濾波進行狀態的實時更新,從而得到天線罩誤差斜率估計,是一種融合機器學習和傳統非線性濾波方法的天線罩誤差斜率估計方法。
2 系統建模
導彈制導控制系統的建模主要包括導引頭、比例導引、自動駕駛儀、彈體動力學環節和彈目相對運動五個部分。如圖1所示,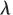 為真實視線角,
為真實視線角,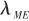 為視線角觀測值,
為視線角觀測值,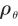 為天線罩誤差斜率,
為天線罩誤差斜率,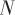 表示比例導引系數,
表示比例導引系數,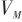 為導彈速度,
為導彈速度,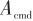 是制導律產生的控制指令,
是制導律產生的控制指令,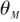 是彈體俯仰角。其中,
是彈體俯仰角。其中,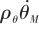 是視線角速度中的耦合分量。這個分量使得彈體姿態耦合到導引頭中,在制導回路內部生成一條寄生回路。指令加速度
是視線角速度中的耦合分量。這個分量使得彈體姿態耦合到導引頭中,在制導回路內部生成一條寄生回路。指令加速度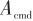 由理想的
由理想的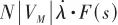 變為
變為
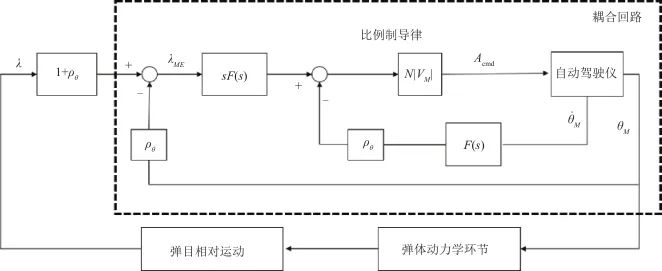
▲ 圖1 制導控制系統▲ Fig.1 Guidance control system
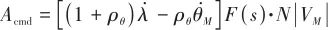 (1)
(1)
式(1)中,姿態角速度也參與到指令加速度的生成,形成了姿態角速率反饋回路。誤差斜率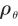 為負時,將導致姿態角速度正反饋,使姿態穩定回路發散;而當
為負時,將導致姿態角速度正反饋,使姿態穩定回路發散;而當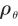 為正時,會降低導彈有效導航比,導致響應緩慢,造成較大的脫靶量。 綜上所述,天線罩誤差的存在破壞了原有的控制結構,嚴重影響了制導控制系統的穩定性和制導精度。
為正時,會降低導彈有效導航比,導致響應緩慢,造成較大的脫靶量。 綜上所述,天線罩誤差的存在破壞了原有的控制結構,嚴重影響了制導控制系統的穩定性和制導精度。
2.1 導引頭
雷達波穿過天線罩會發生折射,此時根據導引頭觀測得到的視在目標位置不是真實的目標位置,如圖2所示,在真實視線和虛假視線之間存在一個誤差角,記作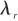 ,即天線罩誤差角。
,即天線罩誤差角。
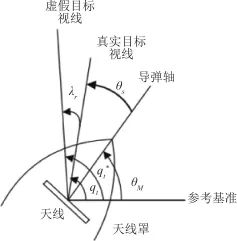
▲ 圖2 帶天線罩的導引頭示意圖▲ Fig.2 Seeker with radome 對于不同的視角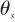 ,由于雷達波穿過天線罩罩壁位置的不同,折射情況不同,天線罩誤差也就不同,天線罩誤差
,由于雷達波穿過天線罩罩壁位置的不同,折射情況不同,天線罩誤差也就不同,天線罩誤差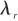 一般為視角
一般為視角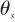 的函數。文獻[19]中給出天線罩瞄準誤差的經驗公式:
的函數。文獻[19]中給出天線罩瞄準誤差的經驗公式:
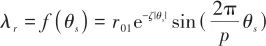 (2)
(2)
式中,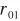 為天線罩瞄準誤差的最大幅值,
為天線罩瞄準誤差的最大幅值,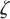 為一個正常數,
為一個正常數,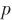 為周期。本文中取
為周期。本文中取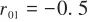 ,
,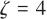 ,
,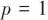 ,此時天線罩誤差隨視角變化曲線如圖3所示。
,此時天線罩誤差隨視角變化曲線如圖3所示。
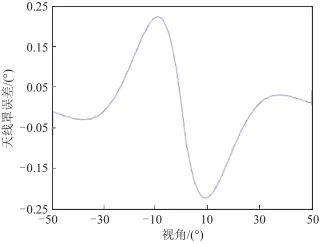
▲ 圖3 天線罩誤差隨視角變化曲線▲ Fig.3 Radome error curve with angle of view 對式(2)求導,得到天線罩誤差斜率的經驗公式:
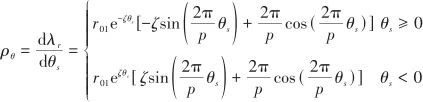 (3)
(3)
天線罩誤差影響下二維彈目幾何關系如圖4所示,真實視線和參考方向的夾角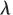 為真實彈目視線角,真實視線與虛假視線的夾角
為真實彈目視線角,真實視線與虛假視線的夾角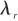 為天線罩誤差角,彈體縱軸和參考方向的夾角
為天線罩誤差角,彈體縱軸和參考方向的夾角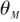 為彈體姿態角,彈體縱軸與導彈速度的夾角
為彈體姿態角,彈體縱軸與導彈速度的夾角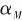 為導彈攻角,導彈速度與參考方向的夾角
為導彈攻角,導彈速度與參考方向的夾角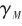 為航跡角,那么視角
為航跡角,那么視角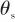 可以表示為
可以表示為
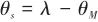 (4)
(4)
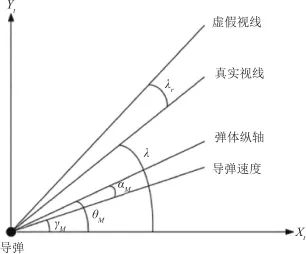
▲ 圖4 天線罩誤差影響下彈目幾何關系▲ Fig.4 Geometric relations of projectiles affected by radome Errors 相應地,實際測量的彈目視線角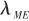 可以表示為
可以表示為
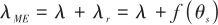 (5)
(5)
式(2)中,天線罩誤差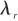 是視角
是視角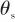 的非線性函數,對天線罩誤差在視角為0處作泰勒展開,當視角
的非線性函數,對天線罩誤差在視角為0處作泰勒展開,當視角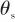 在較小范圍內變化時,利用中值定理余項,實測彈目視線角
在較小范圍內變化時,利用中值定理余項,實測彈目視線角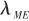 可進一步表示為
可進一步表示為
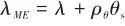 (6)
(6)
2.2 彈目相對運動
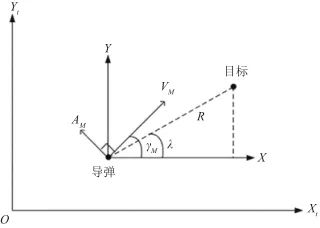
本文針對固定目標制導過程中的天線罩誤差估計問題進行研究,假設目標靜止,建立二維目標接近運動關系。如圖5所示,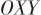 為彈體坐標系,
為彈體坐標系,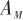 ,
,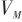 分別為導彈機動加速度和導彈速度,導彈速度與參考方向的夾角
分別為導彈機動加速度和導彈速度,導彈速度與參考方向的夾角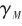 為航跡角,
為航跡角,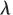 為真實彈目視線角,R為彈目距離。
為真實彈目視線角,R為彈目距離。
▲ 圖5 彈目相對運動示意圖▲ Fig.5 Projectile relative motion 假設目標的速度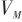 是常數,導彈和目標之間的相對運動建模如式(7)和式(8),相應的Simulink仿真模型如圖6所示。
是常數,導彈和目標之間的相對運動建模如式(7)和式(8),相應的Simulink仿真模型如圖6所示。
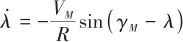 (7)
(7)
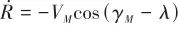 (8)
(8)
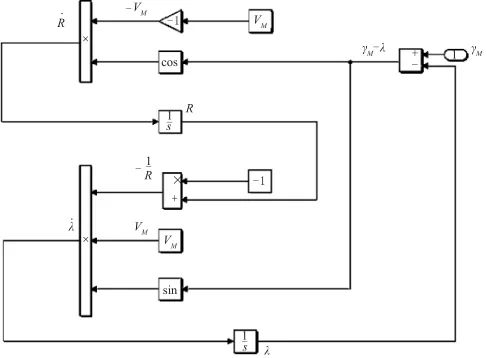
▲ 圖6 彈目相對運動仿真模型▲ Fig.6 Simulation model of projectile relative motion
2.3 導引控制
比例導引律( 是應用最為廣泛的導引方法之一,其基本思想是使導彈速度向量的轉動角速度正比于目標視線的轉動角速度,它能使導彈在目標機動時也能很好地實施攻擊。 根據PNG制導律,利用量測得到的彈目視線角
是應用最為廣泛的導引方法之一,其基本思想是使導彈速度向量的轉動角速度正比于目標視線的轉動角速度,它能使導彈在目標機動時也能很好地實施攻擊。 根據PNG制導律,利用量測得到的彈目視線角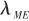 得到控制指令
得到控制指令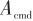 :
:
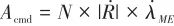 (9)
(9)
式中,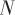 表示比例導引系數,
表示比例導引系數,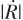 為彈目接近速度,根據式(6),可以推算得到視線角速度
為彈目接近速度,根據式(6),可以推算得到視線角速度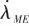 :
:
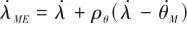 (10)
(10)
代入式(7)得
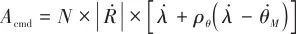 (11)
(11)
2.4 自動駕駛儀
假設自動駕駛儀為一階延時環節,時間常數為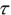 ,則環節傳遞函數為
,則環節傳遞函數為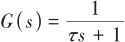 。輸入為制導控制模塊輸出的制導指令
。輸入為制導控制模塊輸出的制導指令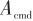 ,輸出為實際控制指令
,輸出為實際控制指令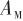 。
。
2.5 彈體動力學模型
彈體動力學模型即機動控制對彈體運動學物理量的作用方程。這里推導從控制指令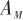 到導彈姿態角(俯仰角)速率
到導彈姿態角(俯仰角)速率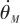 的傳遞函數。 首先,機動加速度
的傳遞函數。 首先,機動加速度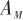 正交于導彈速度
正交于導彈速度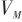 ,可得航跡角速率
,可得航跡角速率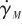 :
:
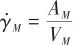 (12)
(12)
彈體姿態角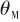 是彈體縱軸和參考方向的夾角,由圖4可知,可以表示為
是彈體縱軸和參考方向的夾角,由圖4可知,可以表示為
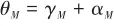 (13)
(13)
導彈機動性參數中的轉彎率時間常數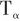 的定義如下:
的定義如下:
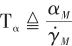 (14)
(14)
代入(13)得
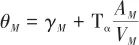 (15)
(15)
對式(15)求導得到姿態角速率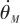 :
:
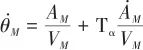 (16)
(16)
對式(16)進行拉普拉斯變換最終得到彈體動力學模型:
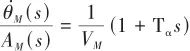 (17)
(17)
2.6 完整的系統建模
考慮比例導引的帶誤差雷達尋的制導系統建模如圖7所示,包括視線角量測、導引控制、自動駕駛儀模塊和彈目相對運動、機體動力學等模塊,至此仿真模型建立完畢。
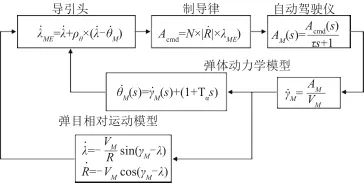
▲ 圖7 考慮比例導引的帶誤差雷達尋的制導系統▲ Fig.7 Radar homing guidance system with error considering proportional guidance 將導彈速度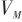 和比例導引系數
和比例導引系數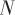 設為常數,取真實視線角
設為常數,取真實視線角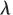 、視角
、視角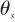 和天線罩誤差斜率
和天線罩誤差斜率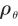 作為3個狀態變量,以視線角觀測值
作為3個狀態變量,以視線角觀測值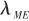 為觀測量,分別建立系統的狀態模型和觀測模型。本節先根據幾何關系建立觀測模型,隨后將利用神經網絡建立狀態轉移模型。 令
為觀測量,分別建立系統的狀態模型和觀測模型。本節先根據幾何關系建立觀測模型,隨后將利用神經網絡建立狀態轉移模型。 令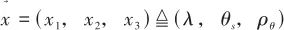 ,根據式(4)和式(6),觀測方程可寫成:
,根據式(4)和式(6),觀測方程可寫成:
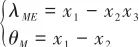 (18)
(18)
3 基于神經網絡和無跡卡爾曼濾波融合的天線罩誤差斜率估計方法
3.1 神經網絡預測
神經網絡,也稱為人工神經網絡 (Artificial Neural Networks,ANN),是一種模仿動物神經網絡行為特征,進行分布式并行信息處理的算法數學模型。其模型結構大體可以分為前饋型網絡和反饋型網絡(也稱為Hopfield網絡)兩大類。本文采用多層前饋神經網絡擬合狀態預測方程。 前饋神經網絡[20](Feedforward Neural Network,FNN),簡稱前饋網絡,是一種最簡單的神經網絡,在各行各業中應用廣泛。 前饋神經網絡采用一種單向多層結構,其中每一層包含若干個神經元,各神經元可以接收前一層神經元的信號,并產生輸出到下一層。其中,第0層為輸入層,最后一層為輸出層,其他中間層叫做隱藏層(或隱含層),隱藏層可以是一層,也可以是多層。 前饋神經網絡中無反饋,信號從輸入層向輸出層單向傳播。一個典型的多層前饋神經網絡如圖8所示,該神經網絡模型共有4層,分別為輸入層、2層隱藏層和輸出層,各個層之間通過權系數進行連接,輸入輸出層在兩端,中間隱藏層的節點數根據實際情況進行選取。
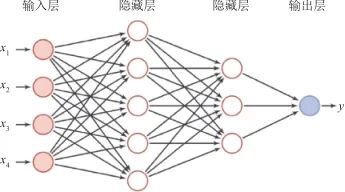
▲ 圖8 前饋神經網絡▲ Fig.8 Feedforward neural network 與傳統的解析建模相比,神經網絡模型可以更好地利用數據,直接學習到映射關系,而不需要進行復雜的分析和推導,避免了人工推導可能出現的錯誤。另外,對于模型過于復雜或者模式未知的系統,神經網絡也可以進行擬合。 因此,本文使用基于前饋神經網絡的狀態預測網絡模型,輸入為一段時間內狀態序列,輸出為整體后移一個時刻的狀態序列。 網絡模型結構如圖9所示,網絡主體由2層節點數為16的Dense層構成,輸出層為節點數為3的全連接層。網絡訓練指標為均方誤差(最小),優化器為Adam優化器。
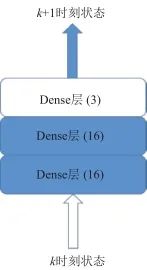
▲ 圖9 網絡模型▲ Fig.9 Network framework
3.2 無跡卡爾曼濾波
無跡卡爾曼濾波的核心是無跡變換(Unscented Transform,UT),其主要思想是先產生一組一、二階矩與狀態變量的信息相同的Sigma點,然后對每個Sigma點進行非線性函數變換,最后用變換后的Sigma點集來確定輸出值的矩。UKF算法的預測步計算均是非線性的,可以避免線性化過程中產生的誤差,提高估算的準確性。 UKF的具體流程為 (1)初始化狀態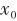 的初始均值
的初始均值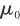 和協方差
和協方差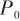 。 (2)計算對應的Sigma點集:
。 (2)計算對應的Sigma點集:
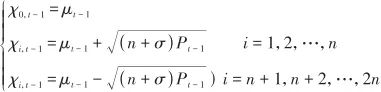 (19)
(19)
式中,n為狀態變量個數,這里為3;σ為一個與n有關的系數。 (3)計算加權系數:
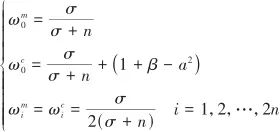 (20)
(20)
(4)預測步:
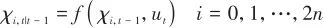 (21)
(21)
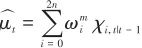 (22)
(22)
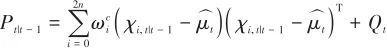 (23)
(23)
式中,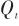 是過程噪聲協方差。 (5)觀測:
是過程噪聲協方差。 (5)觀測:
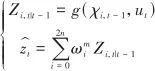 (24)
(24)
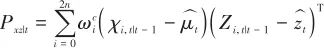 (25)
(25)
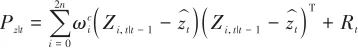 (26)
(26)
式中,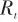 為測量噪聲協方差。 (6)卡爾曼增益:
為測量噪聲協方差。 (6)卡爾曼增益:
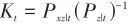 (27)
(27)
(7)更新結果:
 (28)
(28)
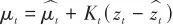 (29)
(29)
3.3 基于神經網絡和無跡卡爾曼濾波融合的估計方法
在本文研究的天線罩模型中,存在狀態方程部分未知的情況,這里利用神經網絡基于歷史數據學習到完整狀態方程,再應用無跡卡爾曼濾波,結合實時觀測得到狀態估計。該估計方法的流程示意圖如圖10所示,用預先訓練好權重的前饋神經網絡作為無跡卡爾曼濾波的預測方程f。
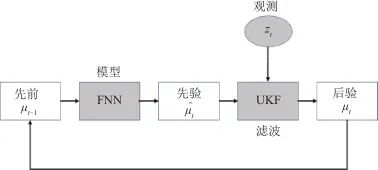
▲ 圖10 基于神經網絡和無跡卡爾曼濾波融合的估計方法流程▲ Fig.10 Method based on neural network and unscented Kalman filter UT變換得到Sigma點集后,計算預測步如下:
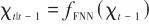 (30)
(30)
結合加權系數得到預測步的均值和方差。隨后的觀測更新步與3.2節相關內容相同,用導引頭觀測值更新狀態估計,從而得到t時刻最終的估計結果:
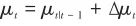 (31)
(31)
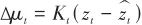 (32)
(32)
然后利用這個估計結果進行下一時刻的狀態預測,迭代計算得到完整的狀態估計序列。
4 仿真結果及分析
因為本文解決的實際問題存在狀態方程部分未知的情況,只使用傳統非線性濾波技術無法完成估計,這里僅與完全依賴歷史數據的神經網絡估計方法設計對比實驗。 考慮到卡爾曼濾波及其變種都是基于馬爾可夫模型,且兼顧實際模型本身的時序特性,僅利用神經網絡技術和本文提出的估計方法都采用時序的輸入輸出進行網絡訓練。
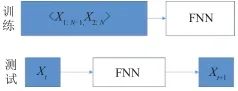
▲ 圖11 神經網絡序列訓練與測試示意▲ Fig.11 Training and testing of FNN 具體地,僅用神經網絡的估計方法的訓練集輸入為當前觀測,輸出為狀態變量。而本文方法采用的訓練集,以輸入為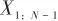 、輸出為
、輸出為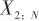 為例,時間上向后預測一步。 本文取序列長度為2生成訓練集訓練模型,然后用較長的完整序列進行測試。 設計64組狀態初值正態分布的訓練集,狀態初值如表1所示。
為例,時間上向后預測一步。 本文取序列長度為2生成訓練集訓練模型,然后用較長的完整序列進行測試。 設計64組狀態初值正態分布的訓練集,狀態初值如表1所示。
▼ 表1 訓練集初值設定▼ Table 1 Initial value of training set

設采樣時間為0.1 s,運行30 s,生成長度為300的序列,分別將上述長序列分割為298個長度為2的短序列,并打亂小序列間順序。按不同初值情況,重復以上步驟64次,并再次打亂,生成包含19072條短序列的數據集。設驗證集比例為10%,測試集比例為10%,最終隨機取1908條序列為驗證集,1907條序列為測試集,剩余80%的15257條短序列為訓練集。對訓練數據的各維度分別進行最大最小值歸一化,即:
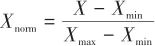 (33)
(33)
測試序列的初值如表2所示,長度為300。
▼ 表2 測試序列初值設定▼ Table 2 Initial value of test sequence

僅用神經網絡估計的狀態曲線如圖12所示,其中,圖12(a)為狀態的估計值和實際值對比,粗實線表示神經網絡方法估計所得,細實線表示實際狀態,可見估計的狀態與實際狀態偏差較大;圖12(b)為3個狀態估計值和實際值的誤差曲線。
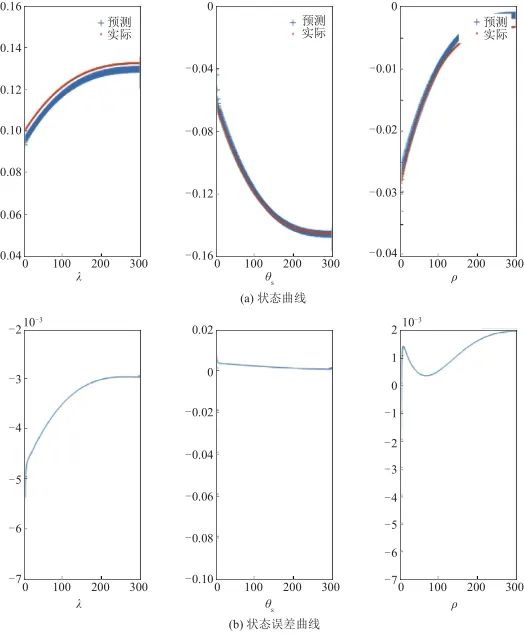
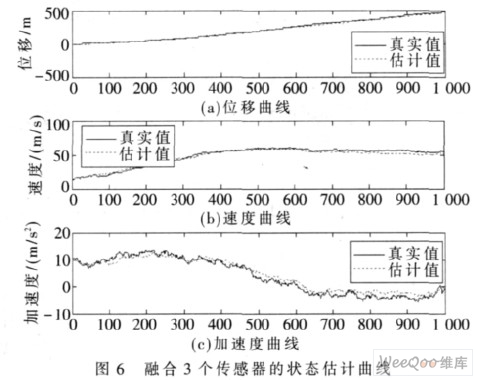
▲ 圖12 僅用神經網絡的狀態測試結果▲ Fig.12 State testing results of neural network 經神經網絡和無跡卡爾曼濾波融合的估計方法得到的狀態曲線如圖13所示,其中,圖13(a)為狀態的估計值和實際值對比,粗線表示本文方法估計所得,細線表示實際狀態,可見估計的狀態與實際狀態較為接近;圖13(b)為3個狀態估計值和實際值的誤差曲線。
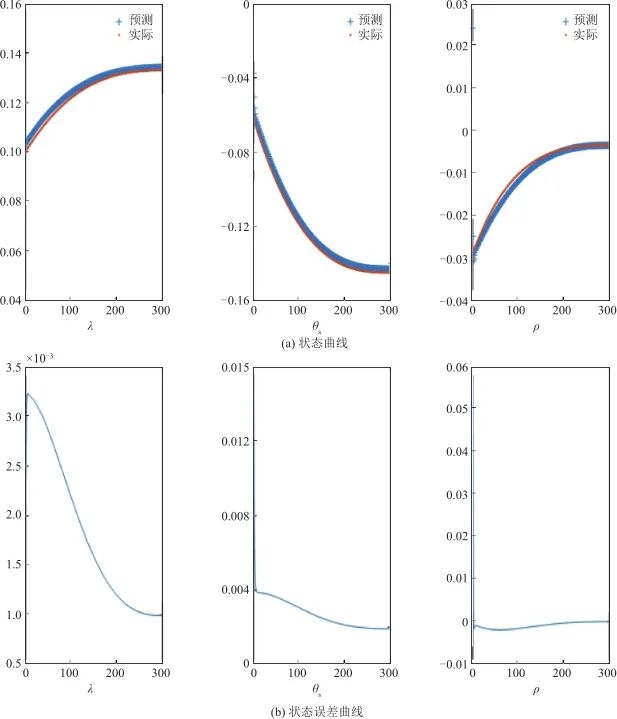
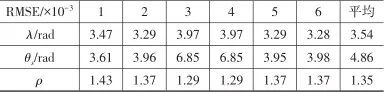
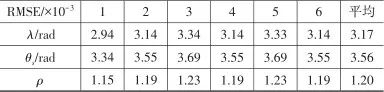
▲ 圖13 本文方法狀態測試結果▲ Fig.13 State testing results of the method 對比可見,本文提出的結合使用傳統非線性濾波技術和神經網絡的方法,估計準確度更高。 分別取多組隨機初值重復實驗,僅采用神經網絡的估計方法和本文方法的估計誤差(這里用均方根誤差RMSE表示)分別如表3和表4所示,其中單純采用神經網絡的方法得到的天線罩誤差斜率估計平均RMSE為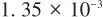 ,本文天線罩誤差斜率估計的平均RMSE更低,為
,本文天線罩誤差斜率估計的平均RMSE更低,為 。
。
▼ 表3 神經網絡實驗結果▼ Table 3 Experimental results of the neural network
▼ 表4 本文方法實驗結果▼ Table 4 Experimental results of the method
5 結 論
針對導引頭天線罩誤差問題,本文首先介紹了該誤差對制導系統的穩定性和精度造成的負面影響,然后以估計天線罩誤差斜率為目標,提出了一種融合神經網絡和無跡卡爾曼濾波的天線罩誤差斜率估計方法。分別以真實視線角、視角和天線罩誤差斜率為狀態變量,視線角為觀測變量,建立非線性濾波模型,其中,預測函數用預先訓練完成的多層前饋神經網絡代替,迭代過程中利用觀測實時更新狀態,從而獲得精度較高的狀態估計。本方法無參數選擇需求,易于工程實現,且對現實數據具有更好的適應性。經多次仿真實驗,證實該方法能夠有效控制預測誤差,具有較高精度。
編輯:黃飛
?
 電子發燒友App
電子發燒友App





















評論