解決幾何變換的一般思路

圖像幾何變換又稱為圖像空間變換， 它將一幅圖像中的坐標位置映射到另一幅圖像中的新坐標位置． 我們學習幾何變換的關鍵就是要確定這種空間映射關系， 以及映射過程中的變換參數。

幾何變換不改變圖像的像素值， 只是在圖像平面上進行像素的重新安排。一個幾何變換需要兩部分運算：首先是空問變換所需的運算， 如平移、旋轉和鏡像等， 需要用它來表示輸出圖像與輸入圖像之間的〈像素〉映射關系：此外， 還需要使用灰度插值算法， 因為按照這種變換關系進行計算， 輸出圖像的像素可能被映射到輸入圖像的非整數坐標上。

主要有以下內容：

·圖像的平移變換

·圖像的鏡像變換

·圖像的轉置變換

·圖像的旋轉變換

·圖像的縮放

1、圖像的平移變換

在進行書寫matlab代碼之前，先來了解一下圖像平移的理論基礎。設圖像的高度為H，寬度為W，如下所示：

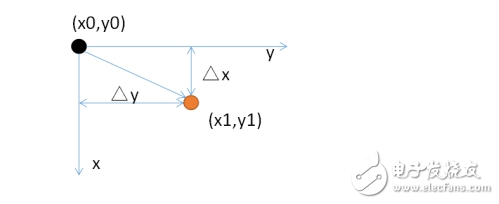
我們知道，圖像是由像素組成的，而像素的集合就相當于一個二維的矩陣，每一個像素都有一個“位置”，也就是像素都有一個坐標。假設原來的像素的位置坐標為（x0，y0），經過平移量（△x，△y）后，坐標變為（x1，y1），如下所示：

?

用數學式子表示可以表示為：

x1 = x0 + △x，

y1 = y0 + △y；

用矩陣表示為：

?

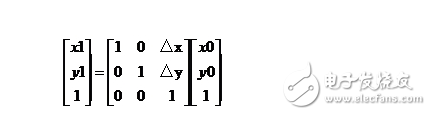
本來使用二維矩陣就可以了的，但是為了適應像素、拓展適應性，這里使用三位的向量。

式子中，矩陣：

?

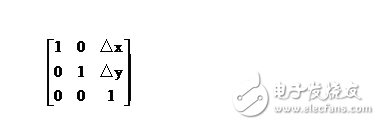
稱為平移變換矩陣（因子），△x和△y為平移量。

此外，我們也知道了，圖像的高度H其實也就是像素的行數，對于坐標1≤X≤H；圖像的長度也就是像素的列數，對應坐標1≤Y≤W。

上面是理論基礎，下面我們就用matlab實現一下圖像的平移變換，相應的matlab代碼如下所示：

close all ;

clear all ;

clc ;

im = imread（‘F:/圖像處理/Koala.jpg’）;%讀入一幅圖

［H，W，Z］ = size（im）; % 獲取圖像大小，H為垂直方向768點，W為水平方向1024點

I=im2double（im）;%將圖像類型轉換成雙精度

res = ones（H，W，Z）; % 構造結果矩陣。每個像素點默認初始化為1（白色）

delX = 50; % 平移量X

delY = 100; % 平移量Y

tras = ［1 0 delX; 0 1 delY; 0 0 1］; % 平移的變換矩陣

for x0 = 1 ： H%第1行到第768行

for y0 = 1 ： W%第1列到第1024列

temp = ［x0; y0; 1］;%將每一點的位置進行緩存，1行1列，1行2列···1行1024列

temp = tras * temp; % 根據算法進行，矩陣乘法：轉換矩陣乘以原像素位置

x1 = temp（1， 1）;%新的像素x1位置，也就是新的行位置（從1~768）

y1 = temp（2， 1）;%新的像素y1位置，也就是新的列位置（從1~1024）

% 變換后的位置判斷是否越界

if （x1 《= H） & （y1 《= W） & （x1 》= 1） & （y1 》= 1）%新的行位置要小于新的列位置

res（x1，y1，：）= I（x0，y0，：）;%進行圖像平移，顏色賦值

end

end

end;

set（0，‘defaultFigurePosition’，［100，100，1000，500］）;%設置窗口大小

set（0，‘defaultFigureColor’，［1 1 1］）;%設置窗口顏色

figure;%打開一個窗口，用來顯示（多幅）圖像

subplot（1，2，1）， imshow（I），axis on ;%顯示圖片，一行兩列，第一幅

subplot（1，2，2）， imshow（res），axis on;%顯示圖片，一行兩列，第二幅

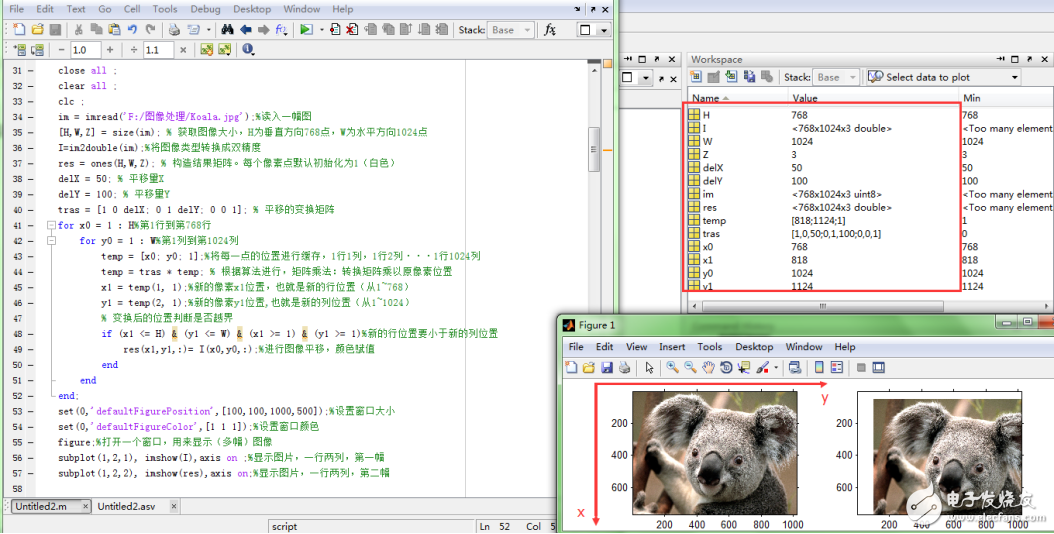
我們先來看一下效果，然后著重分析一下代碼，效果如下所示：

?

然后下面我們分析一下關鍵的代碼：

讀入圖像之后，得到im，我們可以看到im是一個三維的變量，包括了像素的位置（高度（即垂直長度）和寬度（即水平長度）），像素的顏色。（注，24位真彩圖：也是用矩陣表示，圖像像素直接用RGB顏色顯示，而不是通過顏色索引表。圖像像素的顏色用三個變量表示即（R，G，B），每個變量從0~255變化，因此一個像素也就是8bit*3=24bit，一個像素用24bit表示可以有2^24種顏色。）我們可以看到會有unit8，就是8bit的原因。

然后我們獲取圖像的大小，用H，W，Z三個變量接收，其中H接收了圖片的高度（也就是垂直長度），W接收了圖片的寬度（水平長度），然后Z接收了圖片的顏色值。

然后我們將圖像轉換成雙精度類型I，這是因為使用雙精度可以仿真在轉換過程中發生精度損失的問題，也是方便我們進行轉換。轉換之后，我們可以看到unit8的類型別我們轉換成了double類型。

接著，我們構造一個圖像res矩陣，這個圖像首先進行歸一化，也就是讓里面的元素全部為1，對于圖像，就是一張白色的圖片了。這個圖像主要是用來“保存”我們進行位移后的圖像。

然后我們就設置平移量、構造平移變換矩陣。這個矩陣我們根據前面的理論部分可以得到。

接著便是重點了，進行平移變換。我們來一句一句解讀這個循環。當x0=1，y0=1時，得到第一個像素的位置，也就是（x0，y0）這個像素，然后將這個像素位置進行緩存，也就是構造一個矩陣temp，即理論中的：

?

然后進行位置轉換，也就是進行矩陣相乘，用變換矩陣乘以原像素矩陣，得到了變換后像素矩陣：

?

? ? ? 接著，我們需要把變換后的像素位置“提取”出來，用x1，y1進行存儲；為什么要獲取位置呢？這是因為我們要判斷這個像素是否越界了，也就是進行平移之后，得到的這個像素位置是否還存在顯示區域里面，也就是我們的

if （x 《= H） & （y 《= W） & （x 》= 1） & （y 》= 1） 語句

當還在顯示區域里面時，我們要進行移位顯示：

res（x1，y1，：）= I（x0，y0，：）;%進行圖像平移，顏色賦值

這個語句的含義是，把I中的RGB值（也就是顏色值）賦值給res，也就是說，前面矩陣相乘只是移動的像素位置，但是顏色沒有進行移動，這里進行圖像顏色的平移，當x0=1，y0=1時，把該點的位置圖像顏色進行移動過去。

當x0=1，y0=2時，移動第二點。我們可以看到，這里的代碼是：從左到右平移，也就是先進行寬度的平移；從上到下，進行高度的平移。當兩個循環完成之后，圖像也就像平移完成了。

最后的代碼就是顯示圖像了，其中axis on 的意思是打開左邊，方便我們進行查看平移后的位置。從上面的效果我們可以得到，delx表示的高度的平移量，delx為正值時往下平移，delx為負值時往上平移；而dely表示的寬度的平移量，正值往右平移，負值往左平移。