本文介紹了OpticStudio模擬基于偏振的光學(xué)現(xiàn)象的幾種方法。本文的目的是在對基于偏振的光學(xué)進行建模時檢查這些特征的優(yōu)勢和正確應(yīng)用。討論的功能包括偏振光瞳圖、瓊斯矩陣、雙折射、表面涂層等。這些對于波片和隔離器等實際應(yīng)用很重要。

簡介

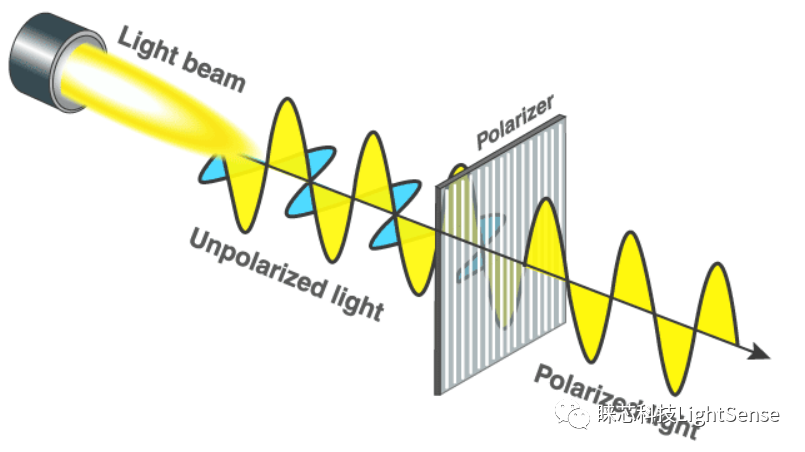
偏振效應(yīng)被用于各個領(lǐng)域的無數(shù)光學(xué)系統(tǒng)中。OpticStudio允許用戶指定進入系統(tǒng)的光的輸入偏振以及序列模式中的表面與偏振特性交互的設(shè)置，提供了對任何應(yīng)用進行建模的方法。建模偏振相關(guān)介質(zhì)的三種方法是通過瓊斯矩陣表面、表面涂層和雙折射輸入/輸出表面。

為了選擇合適的表面類型，了解您嘗試建模的偏振器的用途很重要。本文將描述設(shè)置極化系統(tǒng)以及上述每個表面/表面設(shè)置的優(yōu)缺點。

偏振光源的產(chǎn)生

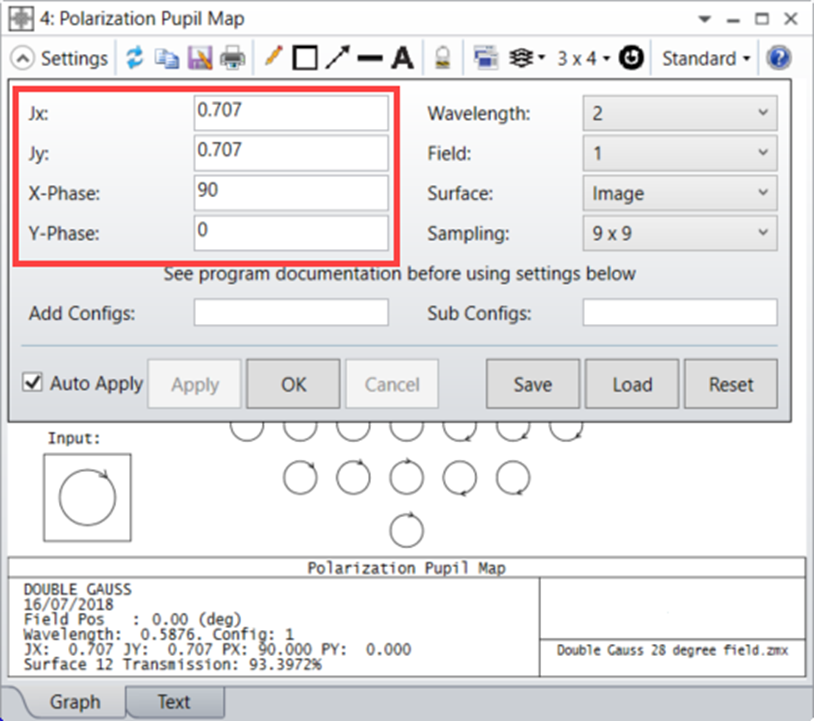
OpticStudio中的所有偏振分析都需要輸入偏振態(tài)，通常以瓊斯矢量 (Jx, Jy) 的形式給出，其中X和Y的起始相位可選。向OpticStudio輸入偏振態(tài)有兩種方式。第一種方法是在單獨的分析設(shè)置中明確定義初始偏振狀態(tài)（Jx、Jy和X/Y相位），例如使用偏振光線跟蹤（Polarization Ray Trace）和偏振光瞳圖（Polarization Pupil Map）。

第二種方法是在系統(tǒng)管理器（System Explorer）的“偏振（Polarization）”部分應(yīng)用偏振狀態(tài)。通過檢查各個分析設(shè)置中的“使用偏振（Use Polarization）”設(shè)置（或類似設(shè)置），在任何適用分析窗口的計算中考慮此處輸入的狀態(tài)。

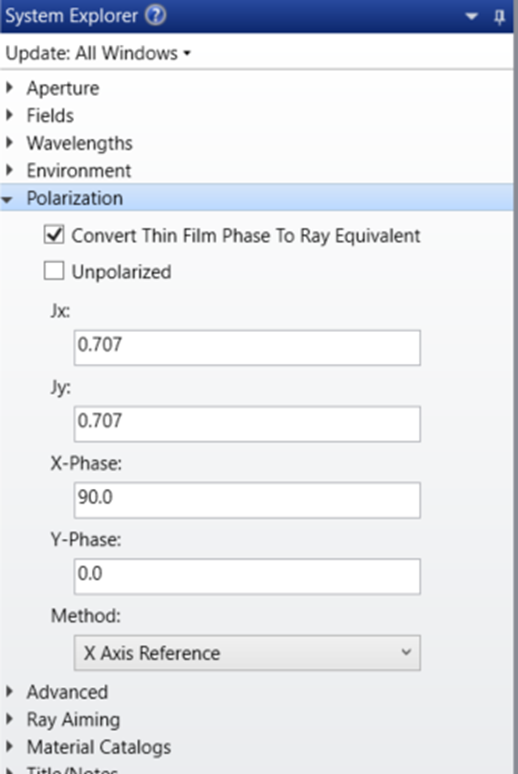
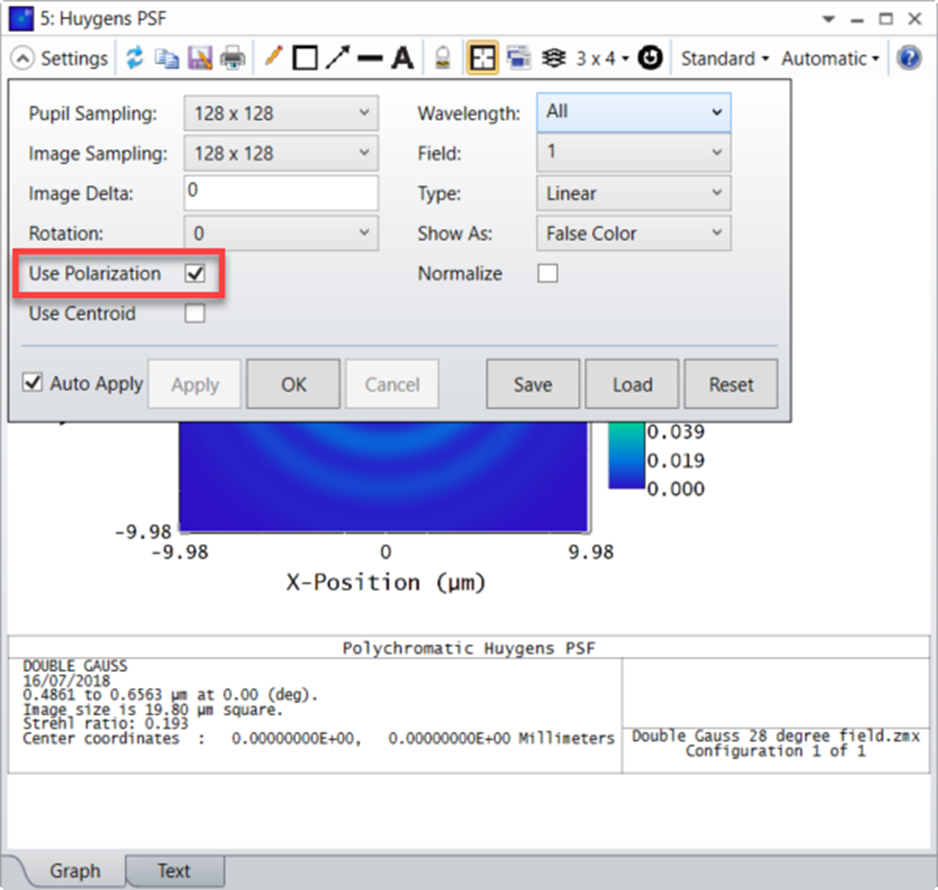
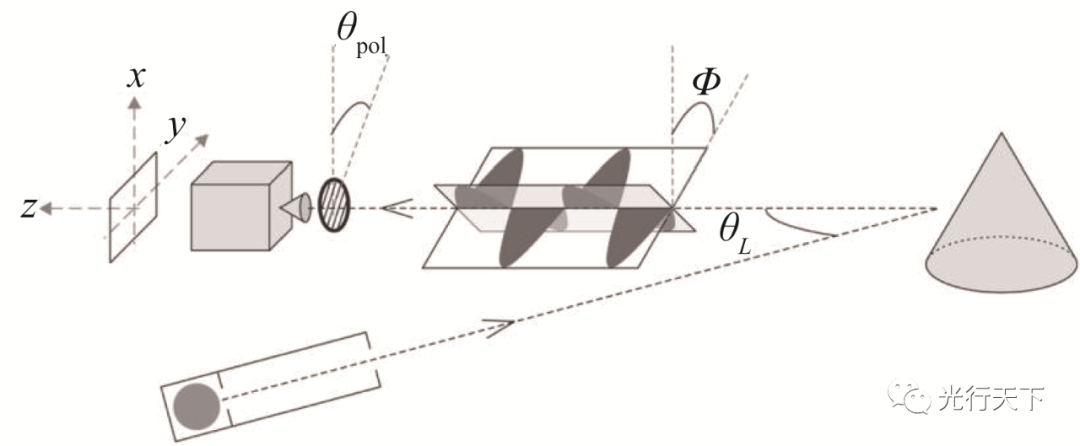
系統(tǒng)管理器中定義的“方法（Method）”（或參考狀態(tài)）需要將2D瓊斯矩陣輸入（Jx、Jy）轉(zhuǎn)換為3D電場分量（Ex、Ey、Ez）。雖然很容易認(rèn)為Jx對應(yīng)于S極化狀態(tài)的能量量，Jy對應(yīng)于P極化狀態(tài)的能量量，但如果沒有入射平面，這些定義是不明確的（參見這個論壇以獲取更多信息）。也就是說，從光源發(fā)射并沿射線矢量K在自由空間中傳播的射線需要參考才能準(zhǔn)確定義偏振態(tài)矢量S和P。在OpticStudio中，可以使用以下參考：

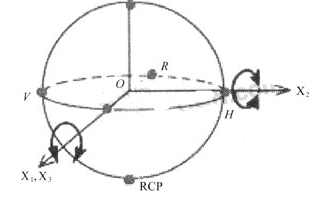
X 軸參考:?P向量由K叉乘X確定，S=P叉乘K（默認(rèn)）；

Y 軸參考:?S向量由Y叉乘K確定，P=K叉乘S；

Z 軸參考:?S向量由K叉乘Z確定，P=K叉乘S。

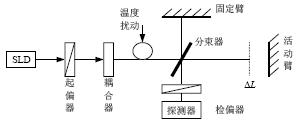
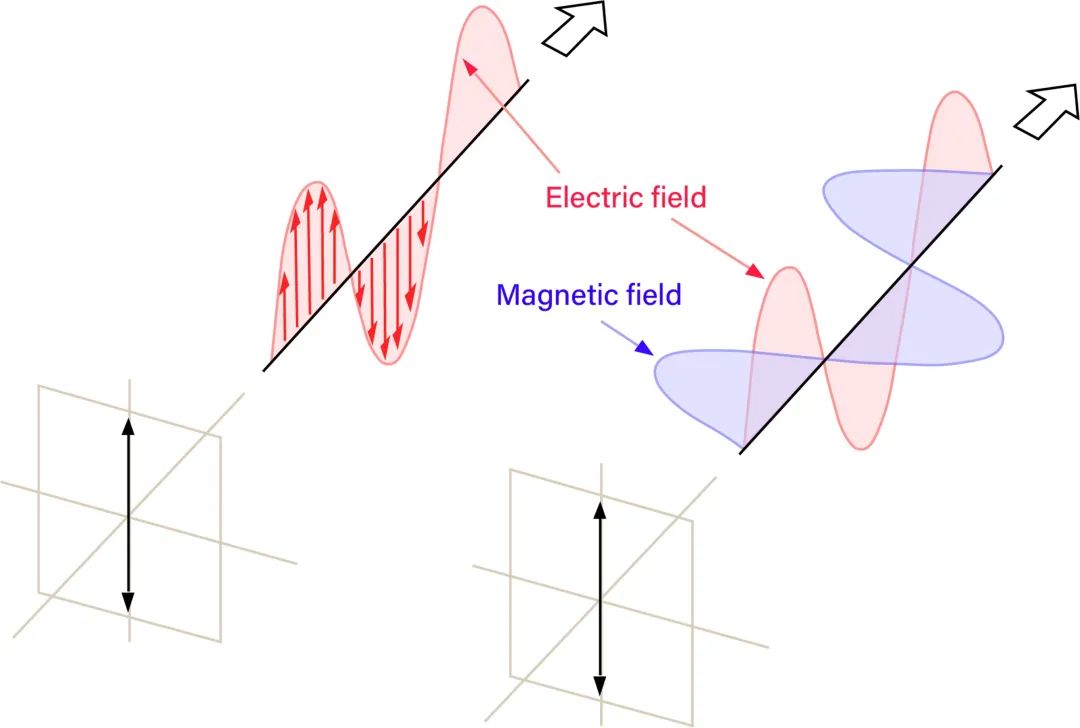
注意：S、P和K（傳播方向）始終是正交的。它們分別由下表中的紅色、藍色和綠色向量表示。

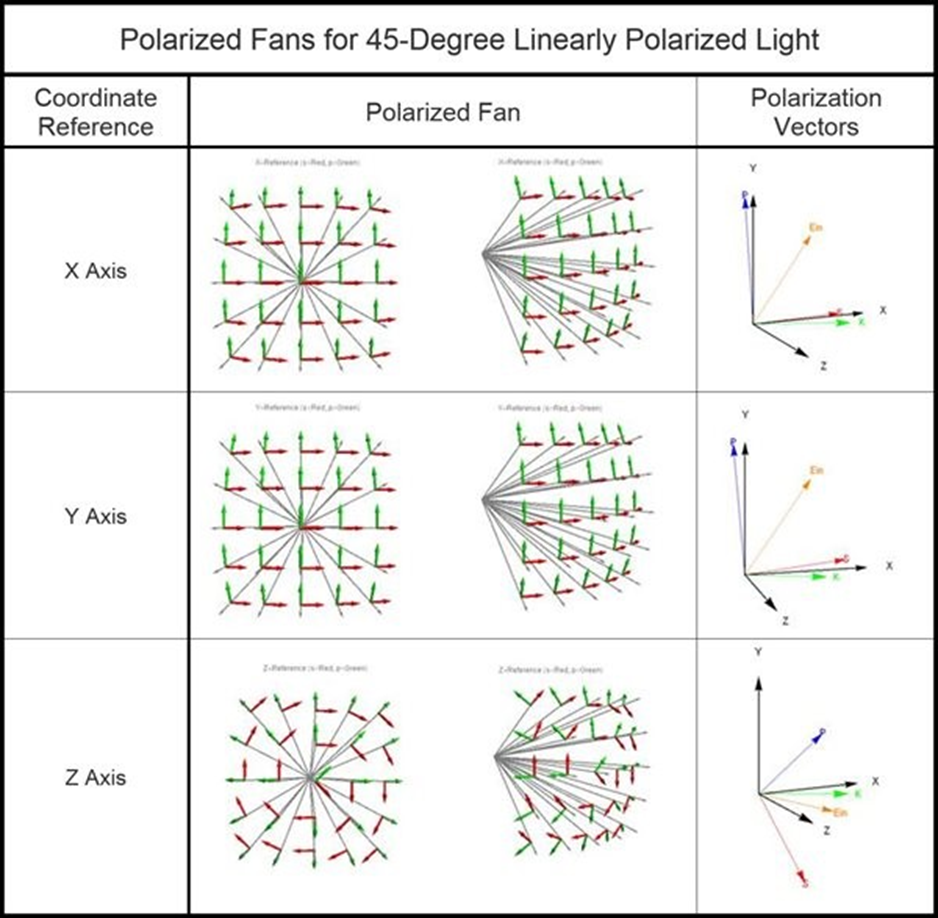
這種方法允許用戶在生成輸入極化時能更加靈活。默認(rèn)表面在z方向具有表面法線，因此經(jīng)典的S和P定義將限制用戶生成Z參考輸入偏振。

偏振光瞳圖

偏振光瞳圖可以說是OpticStudio中最有用的工具，可以快速查看給定表面上光束的偏振狀態(tài)。也就是說，它確實有一些細(xì)微差別，必須完全理解才能準(zhǔn)確解釋其結(jié)果。

通常，OpticStudio執(zhí)行與時間無關(guān)的計算（即它呈現(xiàn)穩(wěn)態(tài)系統(tǒng)的時間快照）。然而，極化瞳孔圖不是這種情況，它在定義的表面上隨著時間經(jīng)過一個周期時在笛卡爾圖上繪制電場矢量 (Ex, Ey) 的端點。這是因為相位隨時間的變化決定了偏振橢圓的方向。對于幾乎所有系統(tǒng)，OpticStudio是在時間上向前還是向后進行計算并不重要，因為它假設(shè)系統(tǒng)處于穩(wěn)定狀態(tài)。默認(rèn)情況下，計算會在時間上向前看（即，如果系統(tǒng)要及時向前推進一些小量，則在“將擊中”指定表面的光線的相位）。

此外，用戶應(yīng)注意，在定義Jx和Jy之間的初始相移時，“X-相位”或“Y-相位”的正值將導(dǎo)致Jx相對于Jy在空間上滯后，反之亦然。例如，定義X-相位=90度和Y-相位=0度將導(dǎo)致電場的Ex分量落后Ey分量90度（見下圖）。

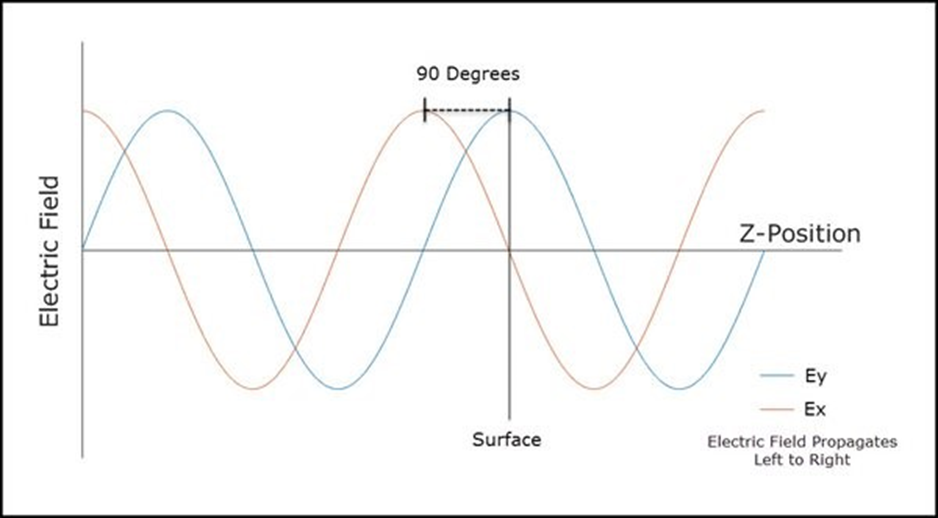
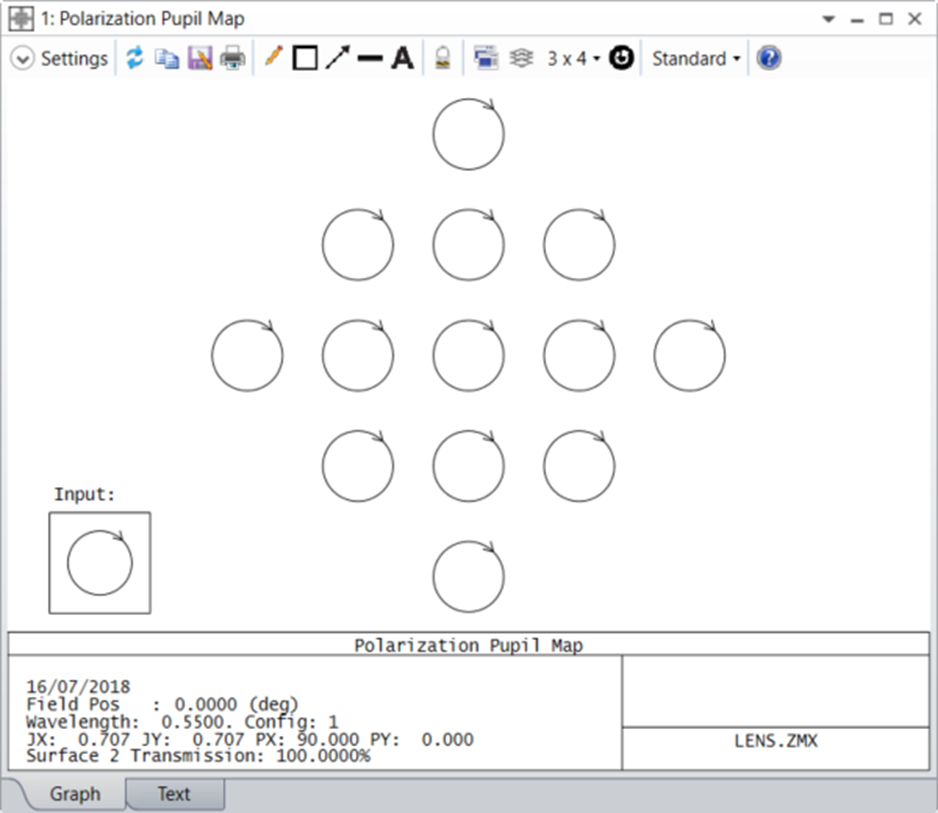
假設(shè) (Jx, Jy) = (0.707,0.707)，產(chǎn)生的偏振橢圓將是順時針、圓偏振，如偏振光瞳圖所示。

偏振相關(guān)介質(zhì)的類型

在OpticStudio中，有多種方法可以操縱給定光束的偏振態(tài)。其中一些方法涉及引入與偏振相關(guān)的表面和材料。在這里，我們將介紹三種這樣的方法并描述它們在OpticStudio中的一般應(yīng)用。

瓊斯矩陣（Jones matrix）

瓊斯矩陣表面是為法向入射光設(shè)計的理想化構(gòu)造。它是一個二乘二的矩陣，它根據(jù)下式修改瓊斯向量（描述電場）

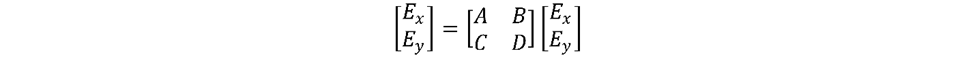
其中A、B、C、D、Ex和Ey都是復(fù)數(shù)（有關(guān)詳細(xì)信息，請參閱“如何使用瓊斯矩陣表面”）。該矩陣可用于解釋具有2-D矢量的3-D現(xiàn)象，假設(shè)光沿Z軸傳播。因此，電場存在于X-Y平面中。如果射線確實與系統(tǒng)的Z軸對齊，則該表面可以為S和P狀態(tài)之間的相對相變以及S和P狀態(tài)的傳輸提供理想的模擬。

OpticStudio將允許用戶將瓊斯矩陣表面應(yīng)用于傾斜的入射角，但根據(jù)定義，此配置中的結(jié)果將代表近似值。該計算未考慮沿z的電場分量矩陣的影響、將光束分裂為普通分量和異常分量（如果對雙折射材料進行建模）以及菲涅耳系數(shù)。

描述延遲器的瓊斯矩陣不應(yīng)與傾斜入射角一起使用。要準(zhǔn)確計算離軸相對相位變化，應(yīng)使用雙折射輸入和雙折射輸出表面。

描述偏振的瓊斯矩陣可以提供一個不錯的離軸近似值。該表面將允許電場在z方向上傳輸，并表現(xiàn)出它們在X和Y電場分量的軸上的表現(xiàn)。然后減去平行于K的電場分量，使電場保持垂直于K。要創(chuàng)建作用于Ez分量的偏振表面，應(yīng)使用鍍膜。

表面鍍膜

OpticStudio允許用戶定義真實和理想化的薄膜光學(xué)鍍膜，并將這些鍍膜應(yīng)用于光學(xué)設(shè)計中的任何表面。OpticStudio還包含大量預(yù)設(shè)的鍍膜目錄，其中包括各種常用鍍膜。有關(guān)定義和應(yīng)用涂層的更多信息，請參見“如何在 OpticStudio 中定義金屬材料”(https://support.zemax.com/hc/articles/1500005488081)。盡管鍍膜可用于多種應(yīng)用，但本次討論將集中于它們?nèi)绾斡绊懝饩€的偏振態(tài)。

在這種情況下討論鍍膜時，必須考慮這樣一個事實，即電場的振幅和偏振狀態(tài)由向量描述：

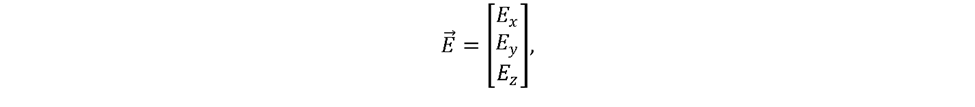
其中Ex、Ey、Ez是復(fù)數(shù)。電場矢量E必須與射線矢量的傳播正交。在兩種介質(zhì)之間的邊界處，電場的透射率、反射率和相位對于場的S分量和P分量是不同的。場的S分量是E沿垂直于入射平面的軸的投影，而P分量位于入射平面內(nèi)。入射平面包含射線傳播矢量和截點處的表面法線矢量。注意：根據(jù)S和P分量的這個定義，當(dāng)光線垂直于表面?zhèn)鞑r，它們之間的區(qū)別變得模糊。

由此，我們可以看到，當(dāng)偏振光入射到表面時，S和P偏振態(tài)是相對于該表面定義的。如果該表面涂有涂層，則透射光的部分可能會發(fā)生顯著變化，具體取決于系統(tǒng)管理器中定義的參考方法。

以一個點物體為例，它位于具有P狀態(tài)通過鍍層的平面前方一定距離處；來自該點的光被定義為具有初始偏振態(tài)Jx=0，Jy=1。使用X或Y軸參考，通過系統(tǒng)傳輸（或阻擋）的S和P偏振光的量在整個表面上顯著變化。這是因為在表面上的所有入射點，輸入偏振Jx和Jy分別保持平行于全局X軸和Y軸。

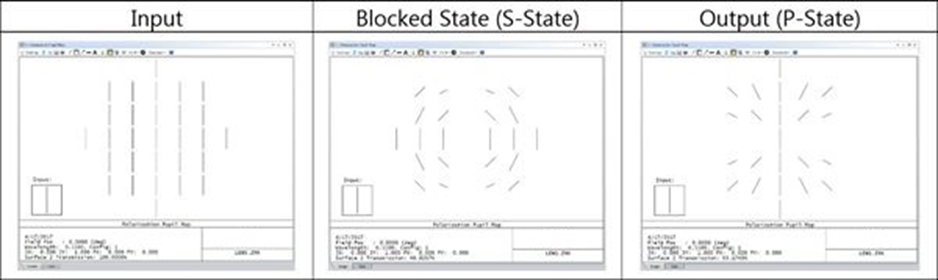
但是，當(dāng)使用Z軸參考時，Jx和Jy狀態(tài)會隨著光線矢量圍繞全局Z軸旋轉(zhuǎn)而發(fā)生變化，因此沒有被阻擋的偏振狀態(tài)。

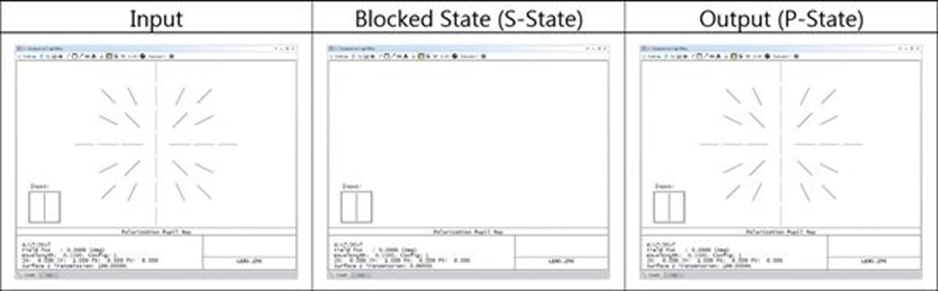
因此，在使用涂層時，必須注意將涂層定義與輸入偏振參考方法正確關(guān)聯(lián)。

在應(yīng)用上述概念時，用戶可以使用Ideal2和Table Coating格式分別指定S和P偏振光的實部和虛部振幅傳輸和反射系數(shù)。這些涂層格式非常適合模擬理想的偏振器。此外，CODA優(yōu)化操作數(shù)可用于優(yōu)化特定偏振值的涂層。

雙折射輸入/雙折射輸出

雙折射材料的運作方式與OpticStudio內(nèi)部的瓊斯矩陣或鍍膜不同。要在序列模式下定義雙折射組件，用戶必須在鏡頭數(shù)據(jù)編輯器中定義兩個表面，一個雙折射輸入表面和一個雙折射輸出表面。在由這些表面界定的物理空間內(nèi)，OpticStudio需要兩種材料，一種用于模擬常規(guī)折射率，另一種用于模擬雙折射介質(zhì)的非常規(guī)折射率。為此，OpticStudio使用為雙折射輸入表面定義的材料指數(shù)作為常規(guī)指數(shù)。然后將“-E”附加到材料名稱并在當(dāng)前加載的材料目錄中搜索該名稱；具有該名稱的材料用于非常規(guī)折射率。

通過這種定義雙折射介質(zhì)的方法，與瓊斯矩陣表面相比，雙折射輸入/輸出表面允許用戶計算菲涅耳系數(shù)和吸收，以提供更準(zhǔn)確的強度傳輸計算。也就是說，用戶可以有選擇地獨立跟蹤普通光束或異常光束，或者跟蹤一個同時考慮由于另一個引起的相位旋轉(zhuǎn)。這是由模式標(biāo)志控制的，它允許用戶在如何根據(jù)給定系統(tǒng)的普通光束和非常光束之間的角度偏差對雙折射效應(yīng)進行建模方面具有更大的靈活性。有關(guān)模式標(biāo)志用途的更多信息，請參見“在“雙折射輸入”表面上選擇模式標(biāo)志有什么作用？。(https://community.zemax.com/got-a-question-7/what-does-selecting-a-mode-flag-on-a-birefringent-in-surface-do-655)

雙折射輸入/輸出表面在模擬雙折射方面的唯一局限是它們不考慮光線分裂的影響。為了考慮光線分裂，系統(tǒng)應(yīng)該轉(zhuǎn)換為非序列模式。

偏振表面相關(guān)應(yīng)用

本節(jié)介紹如何在OpticStudio中定義雙折射延遲器和光隔離器的簡要示例。有關(guān)雙折射偏振器的更深入設(shè)計示例，請參閱“如何設(shè)計雙折射偏振表面”。(https://support.zemax.com/hc/articles/1500005486841)

實用延遲器

光學(xué)延遲器（或波片）是有意將入射光的偏振從一種狀態(tài)改變?yōu)榱硪环N狀態(tài)的光學(xué)組件。此示例描述了如何構(gòu)建具有λ/4相變的有效零級延遲器，也稱為四分之一波片，它將線偏振光轉(zhuǎn)換為圓偏振光。它利用雙折射材料石英和HeNe激光器 (632.8 nm)。

通常，波片的延遲由下式給出：

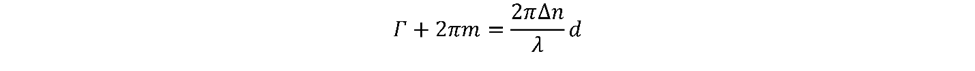
其中，Δn是普通模式和非常模式之間的折射率差，λ是光的波長，d是晶體的長度，Γ是以弧度為單位的延遲。變量m是一個自然數(shù)，表示波片的階數(shù)。根據(jù)這個定義，由于光的2π周期性質(zhì)，相對相位變化不受順序的影響。也就是說，高階波片比低階波片在物理上更厚，它們更容易受到熱膨脹的影響，離軸光束的延遲誤差被放大，如果波長與設(shè)計值不同，延遲誤差也會被放大 。

實際情況中，很少有真正的零級波片被生產(chǎn)出來，因為所需的晶體寬度對于制造來說太薄太脆弱。相反，有效的零級波片是由兩個較厚的單軸晶體（通常是相同的材料）制成的，它們具有交叉的晶軸。它們不如真正的零級波片有效，但由于它們更容易制造，因此它們在性能和可制造性之間提供了良好的折衷。

要在OpticStudio中構(gòu)建這樣的組件，鏡頭數(shù)據(jù)編輯器應(yīng)如下所示。

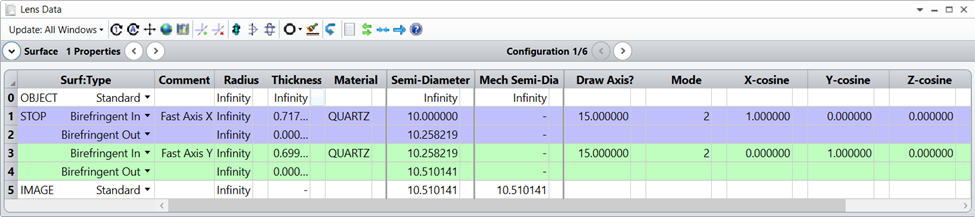
請注意，此鏡頭數(shù)據(jù)編輯器定義了一個10階四分之一波片（紫色），然后是一個10階零相對相位變化片（綠色）。該組合給出了有效的0階四分之一波片。兩個雙折射晶體的厚度計算如下：

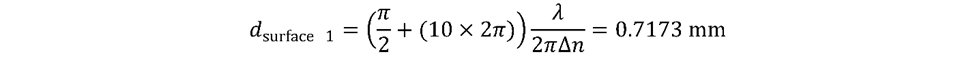
如上所述，OpticStudio一次僅跟蹤一組光線，但雙折射輸入/輸出表面允許用戶同時考慮普通和非正常光線。在該系統(tǒng)中，將Mode Flags設(shè)置為2或3可為系統(tǒng)的輸出狀態(tài)提供非常準(zhǔn)確的模型，因為石英不是強雙折射材料，因此普通光束和非常光束之間的角度偏差很小。此外，晶體內(nèi)的傳播距離相對較小，因此光束將在定義的圖像平面上幾乎完全重疊。使用模式2和45度線偏振輸入光束，輸出是完美的軸上圓偏振光。這與真正的零階波片（見下表）完全匹配預(yù)期結(jié)果。

然而，隨著光束入射角的增加，有效的零級板開始增加比真正的零級板更多的延遲，導(dǎo)致橢圓偏振光并最終接近線性偏振光。在31.5度時，有效的零級片基本上用作半波片而不是四分之一波片。

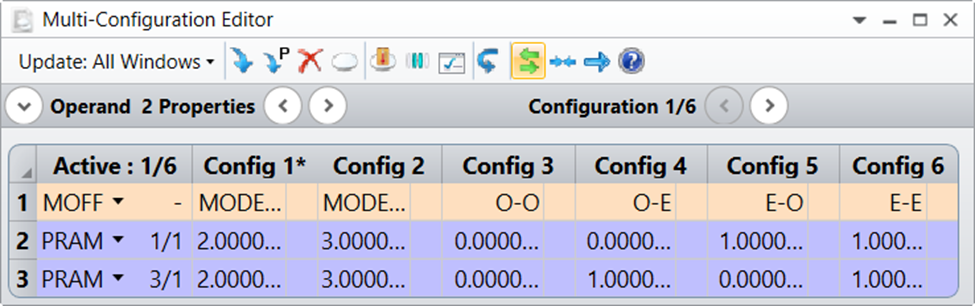
分析這些系統(tǒng)在僅考慮普通或特殊光束時的行為方式也很有趣。比較每種情況的結(jié)果的一種簡單方法是定義多配置編輯器，如下所示。此處，PRAM操作數(shù)應(yīng)用于雙折射輸入表面上的模式標(biāo)志。對于配置3，模式設(shè)置為零（普通光束）；這在注釋行中標(biāo)記為“O-O”。對于配置4，它們分別為表面1和3設(shè)置為0（普通）和1（非尋常）（在注釋行中標(biāo)記為“O-E”），依此類推。

光隔離器

光隔離器是只允許光在一個方向上傳輸?shù)慕M件。此類組件通常會引發(fā)磁光現(xiàn)象，例如法拉第效應(yīng)。盡管OpticStudio目前沒有任何表面可以模擬這種磁光效應(yīng)，但它可以通過瓊斯矩陣表面模擬軸上光隔離器的行為。

隔離器內(nèi)部的光學(xué)材料會根據(jù)傳播方向?qū)θ肷涔馐a(chǎn)生不同的影響。也就是說，對于沿給定方向傳播的線偏振光束，材料會將光束旋轉(zhuǎn)某個角度 α；當(dāng)沿相反方向行進時，材料會使光束旋轉(zhuǎn)-α。以弧度為單位的旋轉(zhuǎn)角 α 定義為：

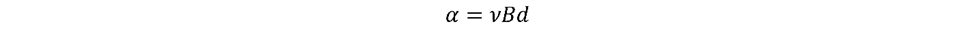
其中ν是Verdet 常數(shù)（以弧度每特斯拉米為單位的旋轉(zhuǎn)比例常數(shù)），B是施加到磁光介質(zhì)的磁通密度（特斯拉），d是介質(zhì)的長度（以米為單位）。

在OpticStudio中，可以通過瓊斯矩陣曲面定義旋轉(zhuǎn)角度：

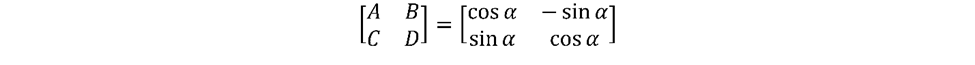
然而，這假設(shè)在z方向上沒有電場傳播。由于額外的離軸傳播距離，這也不會計算媒體本身對z分量或額外旋轉(zhuǎn)的影響。

編輯：黃飛

?