這個問題起源于上一個冰河時代中期的某個時候，就在成功的乳齒象狩獵之后。循環分析或節點分析將產生與此處所示相同的答案，但需要更多的腦力勞動。有時，如果我們保持警惕，會有更簡單的方法。

這個問題實際上證明了對稱性在某些電路分析中可以提供的好處。也就是說，由 12 個相等的電阻組成的立方體對角之間的電阻是多少（圖 1）

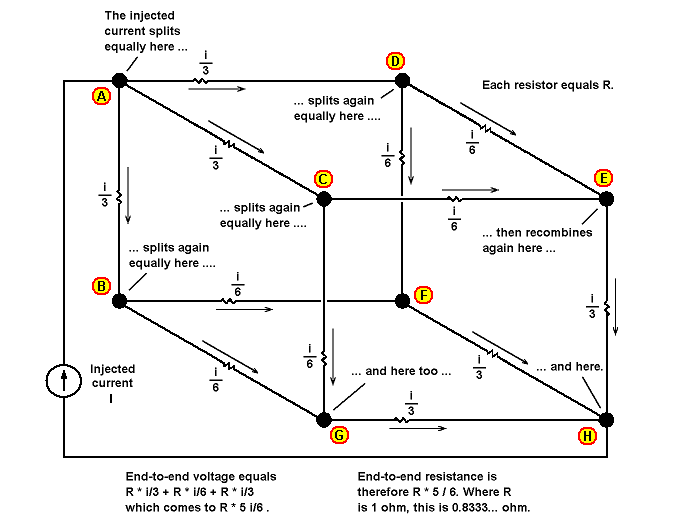
圖 1一個電阻立方體，每個邊緣由 12 個相等的電阻組成，提示我們確定每個角的電阻。資料約翰·鄧恩

您可以編寫節點或循環方程來解決這個問題，但過程會很繁瑣。您必須原諒我，但使用 SPICE 是作弊行為，至少在我看來是這樣。試圖看看哪些內容與哪些內容同時發生可能會讓你語無倫次。然而，使用一些簡單的觀察并識別對稱性適用的位置將順利地得出正確的結果。

在圖 1 中，我們選擇節點 A 和節點 H 作為立方體的對角。我們向這些相對的角落注入電流，為了讓事情變得簡單，我們讓電流為一安培。

首先，我們看看當前的部門。

因為我們具有對稱性，所以我們可以說，遠離節點 A 的三個電阻將分別承載注入電流的三分之一。節點 B、節點 C 和節點 D 將從各自連接回節點 A 的電阻接收三分之一安培的電流。

同樣，由于對稱性，我們可以進一步指出，遠離節點 B、節點 C 和節點 D 的兩個電阻將分別承載其各自節點到達電流的一半。節點 B 將分別向節點 F 和節點 G 傳送六分之一安培，節點 C 將分別向節點 E 和節點 G 傳送六分之一安培，節點 D 將分別向節點 E 傳送六分之一安培和節點F。

接下來，我們看看當前的總結。

節點 E 將接收來自節點 C 和節點 D 的兩個六分之一安培的電流，節點 F 將接收來自節點 B 和節點 D 的兩個六分之一安培的電流，而節點 G 將接收來自節點 B 和節點 D 的兩個六分之一安培的電流。 - 節點 B 和節點 C 各六分之一安培。

節點 H 將從節點 E、節點 F 和節點 G 接收三個各三分之一安培的電流。

可以肯定的是，這整個推理鏈在語言上是拗口的，但對圖 1 進行目視檢查將使這一切變得非常容易理解。

如果我們讓每個電阻器為一歐姆，則承載三分之一安培的每個電阻器上的壓降將為三分之一伏，而承載六分之一安培的每個電阻器上的壓降將為三分之一伏特。六伏特。

如果我們將從節點 H 到節點 A 的電壓降相加，無論我們選擇什么路徑，結果都是六分之五伏。因此，立方體的角對角電阻達到一歐姆的六分之五。