由傳感器所檢測到的奇異信號往往載有設備運行狀態特征的重要信息。判斷狀態信號的奇異點出現時刻，并對信號奇異性實現定量描述，在信號處理和故障診斷等領域有著重要的意義。

　　信號的奇異性分析是提取信號特征的重要手段，傅里葉變換一直是研究信號奇異性的經典工具，但是由于傅里葉變換對信號的表示要么在時域，要么在頻域，缺乏空間局部特性，因而只能確定信號奇異性的整體信息，無法確定奇異點的空間分布。小波變換具有時－頻局部化特性，能夠有效地分析信號的奇異性，確定奇異點的位置與奇異度的大小，為信號奇異性分析提供了有力的工具。

　　一 基本理論

　　（1） 小波分析概況

　　小波分析是自1986年以來由Meyer，Mallat及Daubechies等的研究工作為基礎而迅速發展起來的一門新興學科，他是傅里葉分析（Fourier Analysis） 劃時代的發展結果，是目前數學分析和信號處理領域中廣泛應用的一套新理論、新方法，如：信號分析、圖像處理、量子力學、軍事電子對抗與武器的智能化、計算機分類與識別、數據壓縮、醫學成像與診斷、地震勘探數據處理、邊緣檢測、音樂與語音人工合成、大型機械的故障診斷、大氣與海洋波的分析、分形力學、流體湍流以及天體力學等。但以上大多數領域的應用都可以歸結為信號處理問題，故本文才重點介紹小波分析在信號處理方面的應用。

　　在信號處理領域，對原始信號進行變換，從變換的結果和過程中提取信號的特征，獲得更多的信息，而這些信息是原來信號沒有直接提供的（隱含的），目前，已經有許多變換應用于信號處理，最基本的是頻域變換和時域變換，最熟悉的莫過于傅里葉變換（Fourier Transform），然而，傅里葉變換只能分別對信號的時域和頻域進行觀察，不能把二者有機地結合起來。為了解決此問題，引入了短時傅里葉變換（Short-time Fourier Transform），該變換能夠給出信號的時間和頻率的二維分布，在短時傅里葉變換中，其窗口寬度是一個恒定的值，不能根據信號局部特征調整其窗口寬度。為此，引入了小波變換，解決了以上問題。

　　小波分析方法是一種窗口大小（即窗口面積）固定但其形狀可改變、時間窗和頻率窗都可改變的時頻局部分析方法。即在低頻部分具有較高的頻率分辨率和較

　　低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率，所以被譽為數學顯微鏡。在大尺度下，可以將信號的低頻信息（全局）表現出來，在小尺度下，可以將信號的高頻（局部）特征反映出來。 （2） 信號奇異性的有關定義

　　數學上稱無限次可導函數是光滑的或沒有奇異性，若函數在某處有間斷或某階導數不連續，則稱函數在此處有奇異性，該點就是奇異點。信號的突變點往往包含重要的信息。宇宙射線和太陽黑子爆發，空間核磁暴，對于在太空飛行的衛星和飛船安全構成重大威脅，影響太空飛行器的使用壽命。通過處理采集的空間數據，檢測到奇變點，找到太空天氣異動的時刻，做出科學的判斷，及時調整飛行器姿態，以保護飛行器的安全。尋找變化周期，總結規律，可為進行太空天氣預報提供依據。

　　假設一維信號s（t）=s0（t）+n（t），n（t）為噪聲。s0（t）在t的某一鄰域內二階可導，

　　一階導數‘

　　0（）St的極值代表了在極值某一相鄰區間內，信號線性變化最劇烈的時刻。我們往往對信號變化最劇烈的時刻，也就是’0（）St的模‘0（）St最大值所在時刻感興趣。’0（）St極值點對應于s0（t）的拐點。s0（t）的拐點對應于二階導數‘’0（）St的零點位置。‘’0（）St的零點不一定是‘0（）St的極值點。通過’‘0（）St的零點位置以及零點鄰域內值的正負性質，可以判斷出s0（t）變化的凹凸特性，也可以判斷該點是否是’0（）St在某一鄰域內的極值（極大值或極小值）。但是‘0（）St的極小值并不一定成為’0（）

　　St的最大值。

　　二 小波分析基礎

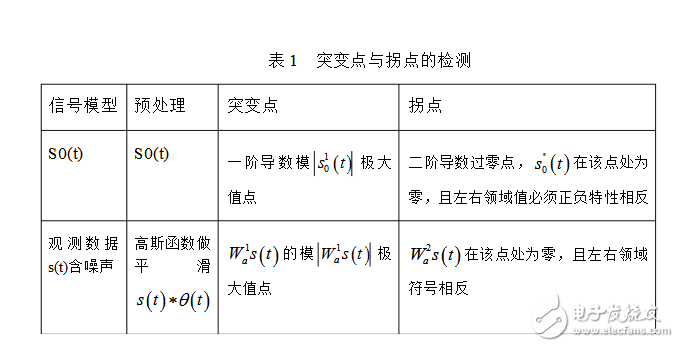
　　從以上分析，用觀測信號的平滑版本stt取代原信號s0（t）、??1Wst和2Wst取代s0（t）的一階和二階導數進行分析。表1比較了含有噪聲的信號和不含噪聲突變點和拐點的區別。為了使結果更準確，綜合考慮??1Wst和??2Wst多尺度計算的結果，來判斷信號的突變點

　　三 仿真實驗與結果分析

　　當小波函數可看作某一平滑函數的一階導數時，信號小波變換模的局部極值

　　點，對應于信號的突變點；當小波函數可看作某一平滑函數的二階導數時，信號小波變換的過零點應于信號的突變點。因此，采用小波變換模的過零點和局部極值點的方法可以檢測信號的突變點。比較來說，用局部極值點的方法進行檢測更具優越性。

　　一般信號奇異性分為兩種情況：①信號在某一時刻其幅值發生突變，引起信號的不連續，這種類型的突變稱為第一種類型的間斷點；②信號外觀上很光滑，幅值沒有發生突變，但是信號的一階微分有突變發生且一階不連續，這種類型的突變稱為第二種類型的間斷點。

　　應用小波分析可以檢測出信號中突變點的位置、類型以及變化的幅度。下面的例子將介紹用小波分析檢測第一類間斷點，信號幅值變化的準確時間，即間斷點的準確位置。在這個例子中信號的不連續是由于低頻特征的正弦信號在后半部分突然加入高頻特征的正弦信號的緣故，分析的目的是將加入高頻特征的正弦信號的時間檢測出來。在MATLAB的命令窗口擬進行如下編程：

　　load freqbrk; %裝載文件名為freqbrk的信號

　　該程序是用db（Daubechies）小波對信號第一類間斷點進行分析，結果如下：

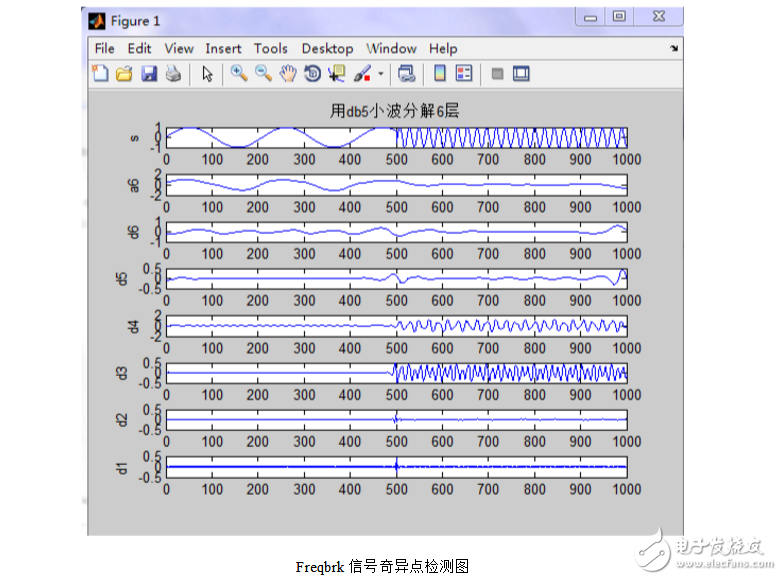
　　從結果波形圖上可以看出，信號的不連續點在500t?。使用db6小波將信

　　號進行6層分解，來檢測第一種類型的間斷點，可以非常清楚地觀察到信號的不連續點，即高頻特征的正弦信號的加入點，這是因為間斷點包含了高頻信息。如果只需要識別第一種類型的間斷點，則可以非常清楚地觀察到信號的不連續點，即高頻特征的正弦信號的加入點，這是因為間斷點包含了高頻信息。如果只需要識別信號的不連續點，用db1小波比用db6小波效果好。

　　原始信號是由兩個獨立的滿足指數方程的信號在t=500處連接起來的，因此它看上去是光滑的，但它的一階微分有突變。采用db6小波對信號分解后，在信號的第一層高頻系數d1中可以明顯的看到t=500的間斷點。要注意的是，在信號奇異點的檢測中，選擇小波的正則性非常重要，因為這時小波可實現一個長的沖

　　激響應濾波器。

　　四 結束語

　　從實際數據的圖形結果，可看出：??2Wst的結果能夠精確定位拐點，但是拐點不一定是突變點，只有表現為凸特性的拐點才是突變點；而突變點一定是拐點。??1Wst和??1Wst是很難精確定位突變點的位置，但是可以判斷拐點是否為突變點。所以，要綜合考慮??1Wst和??2Wst在尺度上的計算結果，??2Wst用于精確定位拐點（鑒別凸性的拐點），而??1Wst和??1Wst用于判斷該拐點是否是模極大，是否是突變點。這樣既可以保證結果穩健，又能精確定位奇異點的位置。 信號奇異點可通過信號的小波變換局部極大值來定位，而奇異性運用該點的Lipschitz α來定量描述。運用該理論來實現信號的奇異性檢測，比常規手段更優越。需要注意的是：選擇不同的小波分析信號的奇異性及奇異性位置和奇異度的大小，其檢測效果也不一樣，因此，選擇合適的小波非常重要。