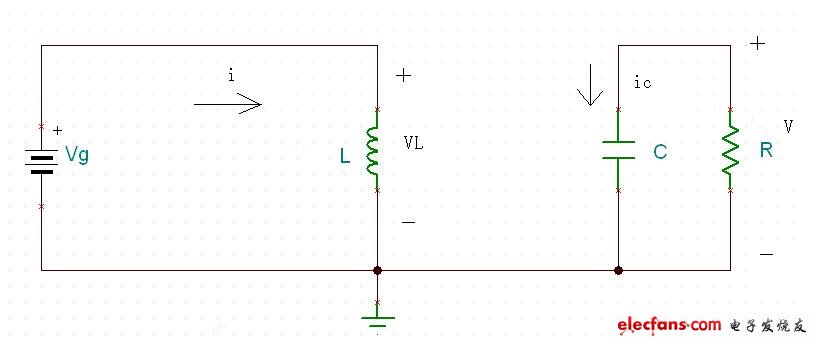
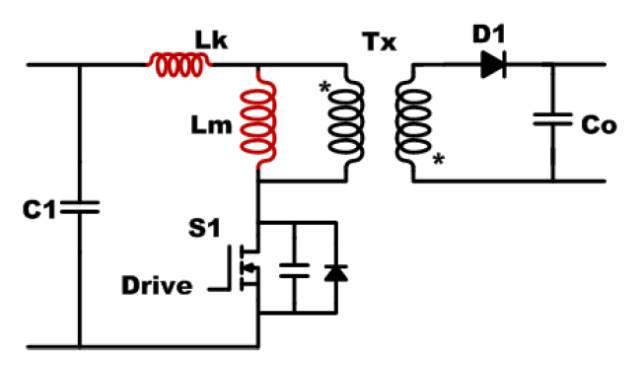
?
圖八

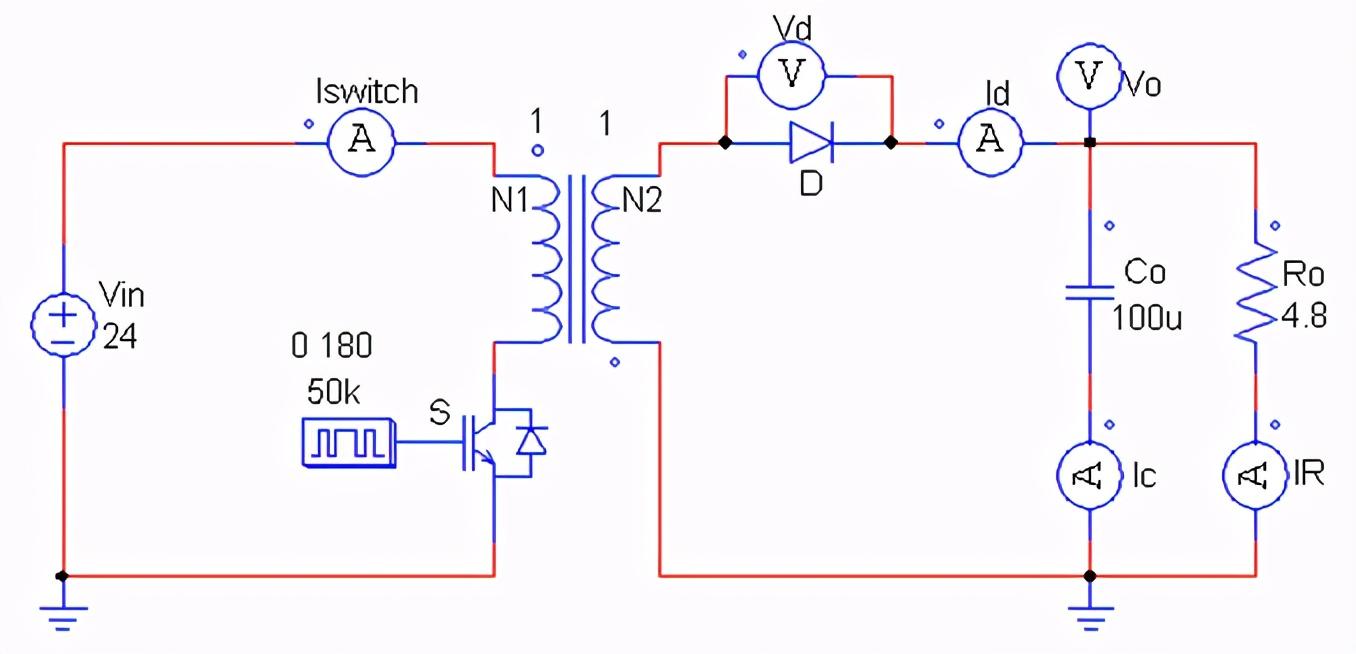
列寫狀態方程:
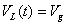?? (1)
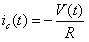????(2)
因為有前面的假設,所以2可以簡化為:
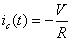?? (3)
狀態1的持續時間為 dTs.

第二個工作狀態:Mosfet Q關斷,二極管D開通.如圖九所示:

圖九

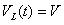????(4)
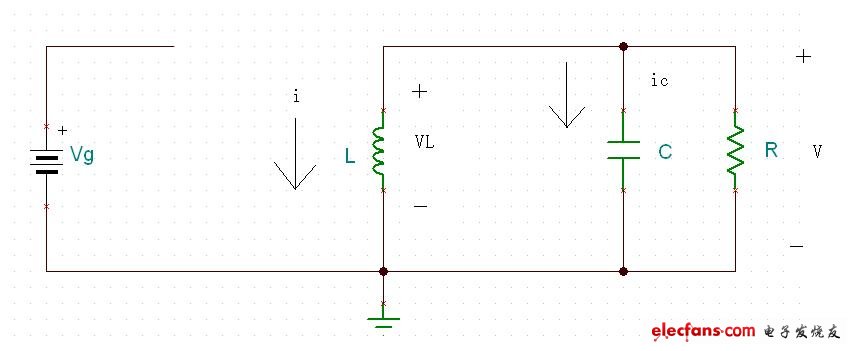
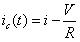????(5)
狀態2持續時間為(1-d)Ts,記為d'Ts.

由于這是一個和諧的電路,所以有:
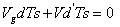?? (6)
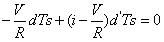?? (7)
解等式 6 和 7 ,并利用 d+d' =1可得:
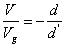????(8)
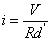????(9)
從等式 8 看到了在CCM模式下面buck-boost的直流增益,因為flyback是從buck-boost變來的,所以我們猜測flyback的直流增益應該和這個有些像(具體見后文推導).?

從等式 9 看到了在CCM模式下面buck-boost的電感的平均電流就等于輸出的電流除以d'.接著馬上研究一下mosfet和D所承受的電壓.

?

在狀態1,二極管D關斷,所承受的反壓為:
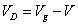????(10)
利用等式8的結果,則(10)可以寫為: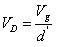???? (11)
同理可在狀態 2 計算Mosfet所承受的電壓: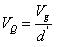????(12)

等式 11 和等式 12 在告訴我們,占空比 d 越大,輸出電壓V的值越高,Mosfet和二極管D所承受的電壓越高(好像是廢話,輸出電壓越高,直觀來說器件所承受的電壓也越高嘛).等式 11 和等式 12,不僅僅驗證了這個直觀的想法,而且定量的給出了電壓的大小,這個是有意義的事情.

下面研究一下這個電路中的電流吧.

電感的平均電流i等式9 已經給出,是和輸出電流相關,那電感的紋波電流呢?

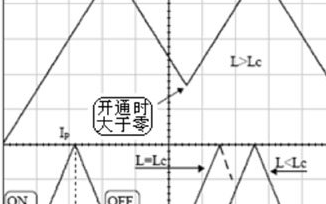
在狀態1,電感電流的示意圖如圖十所示(在畫圖板里面畫的圖,難看一點了,能看明白就好了,將就用下吧):

圖十

從圖十中計算:
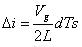????(13)
這個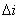的大小是可以被設計的.而且,如果電路是理想無損耗的話,當輸入電壓和輸出電壓確定后,這個值是不隨著輸出電流變化的,它被電感所確定了!這個很重要,對后面的DCM狀態的分析很重要.前面有假設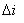相對i很小,那現在給出一個具體的值,比如 設計成i的5%.

有效值(RMS)的計算,按照公式是這么算:
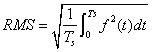?? (14)

在電源中,最常見的是梯形波(三角波是梯形波的一種特殊形式),每次都按 14 的方法計算RMS值是不是覺得很煩呢?有沒有簡單的方法啊?答案,有,下面就是一個很簡單的計算諸如梯形波一類分段線性函數的有效值的方法.真的很簡單,像梯形波這樣子,一般用心算就可以得出來近似值了哦...?

一個如圖十一的波形,有效值可以這樣子計算:

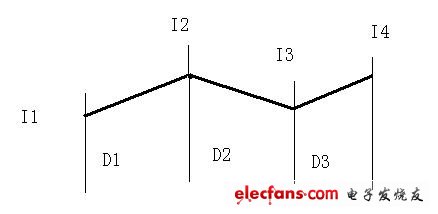?? 圖十一

?

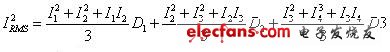????(14a)

其中D1,D2,D3,分別表示該段經歷的時間占總時間的比例.

好,馬上來利用一下我們的秘籍來計算通過Mosfet,二極管D和電感的RMS電流.這個事情很有意義.

已經假設為5%的i的大小,則通過Mosfet的RMS電流
??(15)
有發現什么沒有?這個值是不是非常接近于用電感電流的平均值i來計算的RMS值啊(說明在小紋波的情況下,用平均值來代替RMS值,是一個好辦法.因為通常來說,平均值都比RMS值好計算^_^).

同理,流過二極管D的RMS電流可以表示為:
?? (16)
流過電感L的RMS電流可以表示為:
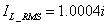????(17)

到這里,幾乎所有的原件都計算了,除了C.下面就來計算C的一些東西.

C上的紋波電壓.利用我們前面的假設,在d'時間段內,有:
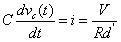????(18)
所以有:
????(19)
對C進行充放電的電流只是紋波電流,其直流成分都供給了負載,所以有:
????(20)
其中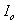 表示輸出電流并且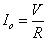

好,到現在為止,你已經是一個CCM模式的buck-boost的初級設計師了。