電子發燒友App
大家最早可能接觸,也是可能接觸最多的電路拓撲應該是flyback.至少我剛剛接觸電源的時候,最先就是flyback.不會設計,連分析也不懂,唯一能做的是模仿(額,難聽點就是抄襲了:( ).這樣子的狀態持續了一段時間后,才開始慢慢的有一些了解.為了讓初學者能更快的上手,少走彎路,于是有了這一章.
為了分析flyback電路,我們從flyback的源頭開始說吧.Flyback是從最基本的三種電路中的buck-boost演變而來的.所以對buck-boost的分析,一定有助于對flyback的分析,而且buck-boost看起來似乎要比flyback簡單,至少它沒有變壓器吧.
為了證明我沒有騙你,下面將要開始來對buck-boost進行演變,最終會演變成flyback.
?
?圖一
圖一 是buck-boost的原型電路. 把電感L繞一個并聯線圈出來,如圖二:
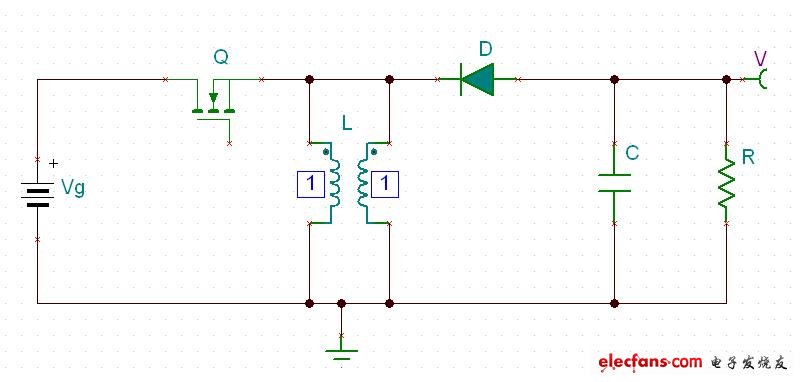?圖二
把L的2個并聯線圈斷開連接,并且改變圈數比,改為:1:n,如圖三:
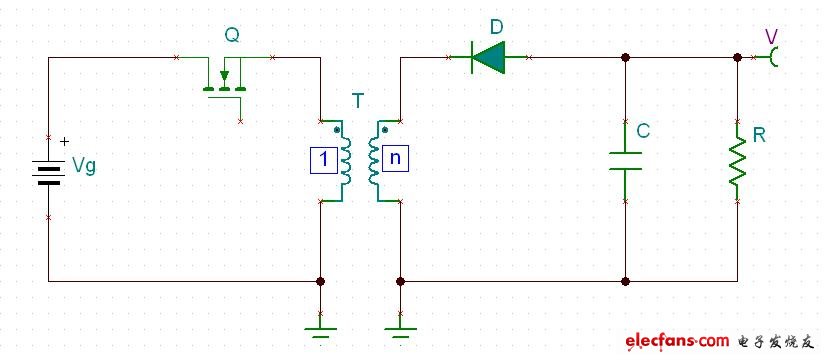
?圖三
把圖三中的二極管沿著所在回路移動,變成陰極朝外的樣子,并且,改變輸出電壓V和接地的位置如圖四:
?
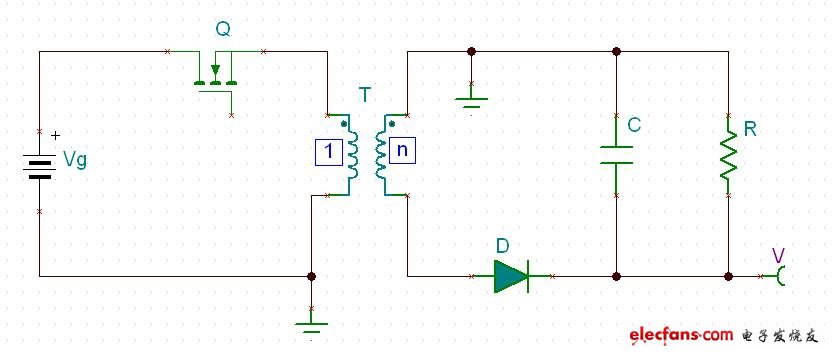?圖四
把圖四中的Q順著回路移動到變壓器下方,如圖五:
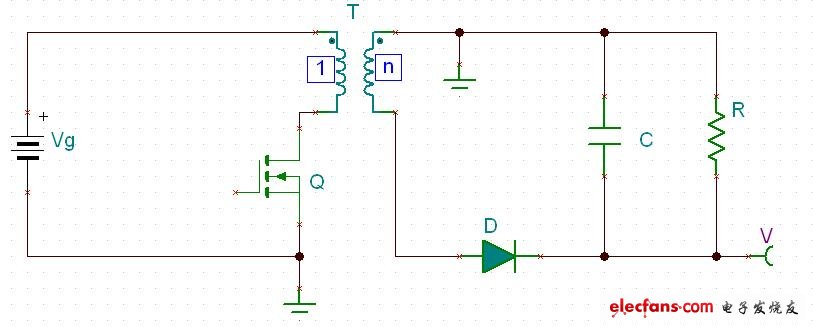?圖五
把圖五的電路,重新整理一下成圖六.^_^,這樣子和你見到的flyback有點像了吧.
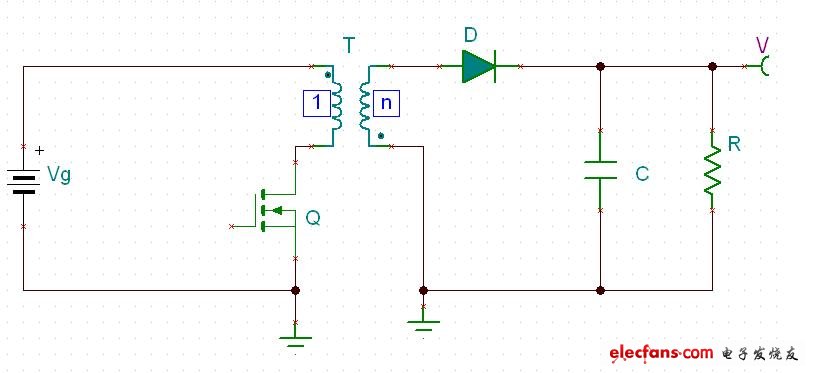??圖六
以上說明,我們研究buck-boost的行為特性,對研究flyback的行為特性有很大的幫助.
1. 電路工作在連續狀態(CCM),也就是說電感電流L是連續的,任何時候電感中總存在電流.(電路的另一種工作狀態DCM將在以后的章節中分析)
2. 在一的假設下,電路工作就可以分成2個狀態,狀態1,Q開通,二極管D關斷,這個狀態時間長度為t1, ,Ts為周期,這個狀態記為d,狀態2,Q關斷,二極管D開通,這個狀態記為 ,d' ＝1-d.
3. 電感L中的電流 紋波和電容C上的電壓紋波相對其直流分流來說都很小.一個好的設計,要求輸出的電壓紋波總是很小,所以,C的紋波小,總是成立的.
4. 所有的損耗都不討論先.即,電路所有原件是理想的.
5. 電路工作在一個穩定的狀態下.
第一個工作狀態:mosfet Q開通,二極管D關斷.如圖八所示:
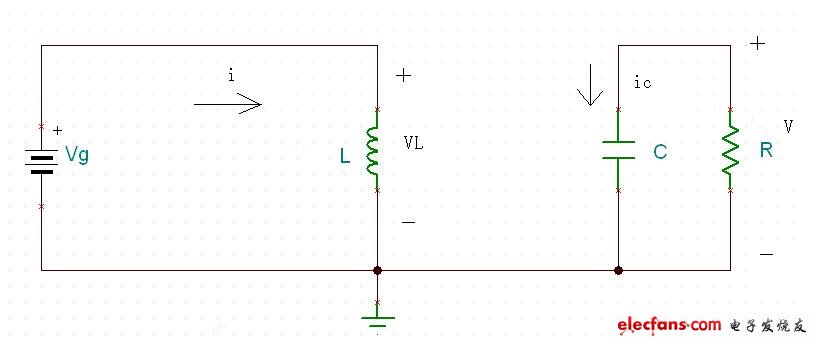?圖八
列寫狀態方程:
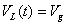?? (1)
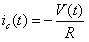????(2)
因為有前面的假設,所以2可以簡化為:
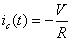?? (3)
狀態1的持續時間為 dTs.
第二個工作狀態:Mosfet Q關斷,二極管D開通.如圖九所示:
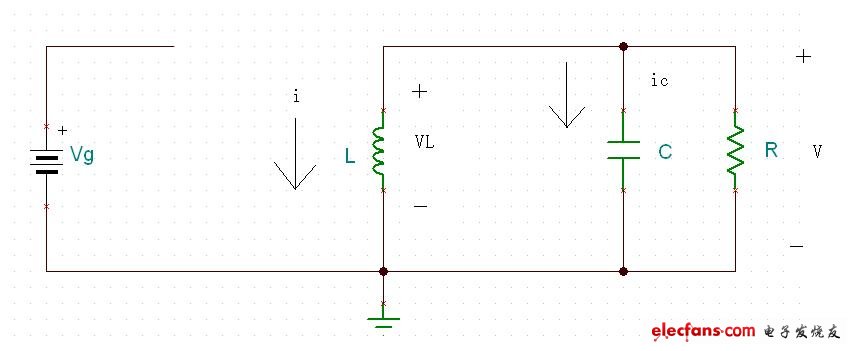
圖九
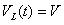????(4)
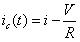????(5)
狀態2持續時間為(1-d)Ts,記為d'Ts.
由于這是一個和諧的電路,所以有:
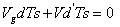?? (6)
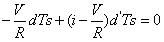?? (7)
解等式 6 和 7 ,并利用 d+d' =1可得:
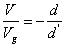????(8)
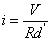????(9)
從等式 8 看到了在CCM模式下面buck-boost的直流增益,因為flyback是從buck-boost變來的,所以我們猜測flyback的直流增益應該和這個有些像(具體見后文推導).?
從等式 9 看到了在CCM模式下面buck-boost的電感的平均電流就等于輸出的電流除以d'.接著馬上研究一下mosfet和D所承受的電壓.
?
在狀態1,二極管D關斷,所承受的反壓為:
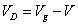????(10)
利用等式8的結果,則(10)可以寫為: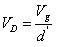
???? (11)
同理可在狀態 2 計算Mosfet所承受的電壓: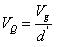
????(12)
等式 11 和等式 12 在告訴我們,占空比 d 越大,輸出電壓V的值越高,Mosfet和二極管D所承受的電壓越高(好像是廢話,輸出電壓越高,直觀來說器件所承受的電壓也越高嘛).等式 11 和等式 12,不僅僅驗證了這個直觀的想法,而且定量的給出了電壓的大小,這個是有意義的事情.
下面研究一下這個電路中的電流吧.
電感的平均電流i等式9 已經給出,是和輸出電流相關,那電感的紋波電流呢?
在狀態1,電感電流的示意圖如圖十所示(在畫圖板里面畫的圖,難看一點了,能看明白就好了,將就用下吧):
圖十
從圖十中計算:
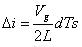????(13)
這個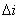
的大小是可以被設計的.而且,如果電路是理想無損耗的話,當輸入電壓和輸出電壓確定后,這個值是不隨著輸出電流變化的,它被電感所確定了!這個很重要,對后面的DCM狀態的分析很重要.前面有假設
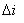相對i很小,那現在給出一個具體的值,比如 設計成i的5%.
有效值(RMS)的計算,按照公式是這么算:
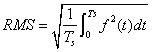?? (14)
在電源中,最常見的是梯形波(三角波是梯形波的一種特殊形式),每次都按 14 的方法計算RMS值是不是覺得很煩呢?有沒有簡單的方法啊?答案,有,下面就是一個很簡單的計算諸如梯形波一類分段線性函數的有效值的方法.真的很簡單,像梯形波這樣子,一般用心算就可以得出來近似值了哦...?
一個如圖十一的波形,有效值可以這樣子計算:
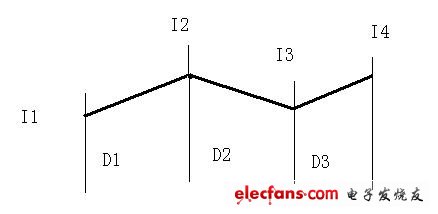?? 圖十一?
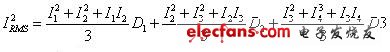????(14a)其中D1,D2,D3,分別表示該段經歷的時間占總時間的比例.
好,馬上來利用一下我們的秘籍來計算通過Mosfet,二極管D和電感的RMS電流.這個事情很有意義.
已經假設為5%的i的大小,則通過Mosfet的RMS電流
??(15)
有發現什么沒有?這個值是不是非常接近于用電感電流的平均值i來計算的RMS值啊(說明在小紋波的情況下,用平均值來代替RMS值,是一個好辦法.因為通常來說,平均值都比RMS值好計算^_^).
同理,流過二極管D的RMS電流可以表示為:
?? (16)
流過電感L的RMS電流可以表示為:
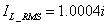????(17)
到這里,幾乎所有的原件都計算了,除了C.下面就來計算C的一些東西.
C上的紋波電壓.利用我們前面的假設,在d'時間段內,有:
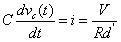????(18)
所以有:
????(19)
對C進行充放電的電流只是紋波電流,其直流成分都供給了負載,所以有:
????(20)
其中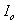
表示輸出電流并且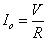
好,到現在為止,你已經是一個CCM模式的buck-boost的初級設計師了。
下面開始我們的flyback的分析之旅.首先推出一個叫做簡單變壓器模型的東西,用這個東西可以簡單的模擬變壓器,就能對有變壓器的電路開始做分析了.圖十二,給出了這個簡單的模型.?
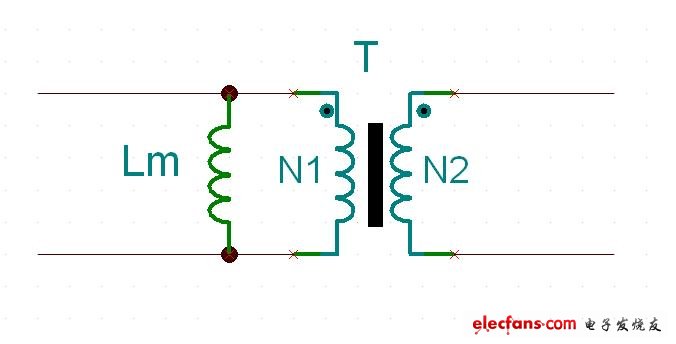
圖十二
其中Lm代表著勵磁電感,其它部分則是一個理想變壓器.對一個設計良好的變壓器來說,需要的勵磁電流,總是占總電流的很小的一部分.這個簡單的變壓器模型忽略了諸如漏感,耦合電容,層間電容,電阻等參數.但是,這個模型做為開始的分析讓然是一個好的選擇.
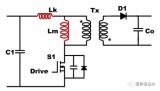
下面就把這個簡單的變壓器的模型插入到我們的flyback的電路(圖六)當中,并規定電壓電流的正方向,如圖十三所示.
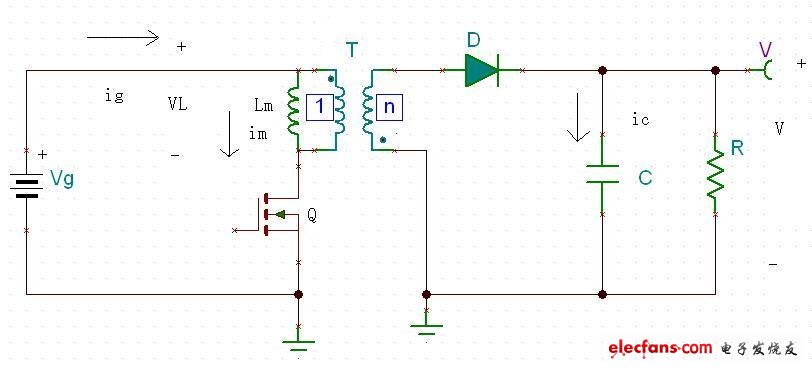?? 圖十三假定這個flyback電路仍然工作在穩定的CCM狀態.
在狀態1 mosfet Q開通,二極管D關斷,電路如圖十四所示.
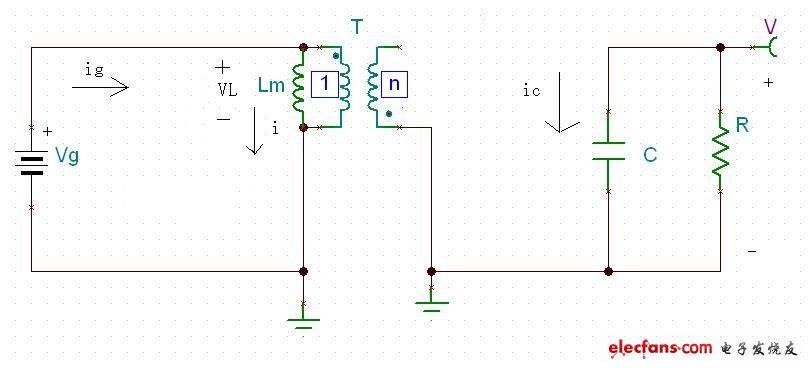???圖十四
應用我們最開始的假設,然后列寫狀態方程:
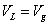?? (21)
????(22)
????(23)
這個狀態持續時間為dTs.Lm中的電流i在Vg的作用下,線性增加,斜率為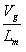
.能量儲存在Lm中.
在狀態2 Mosfet Q關斷,二極管D開通,電路如圖十五所示.
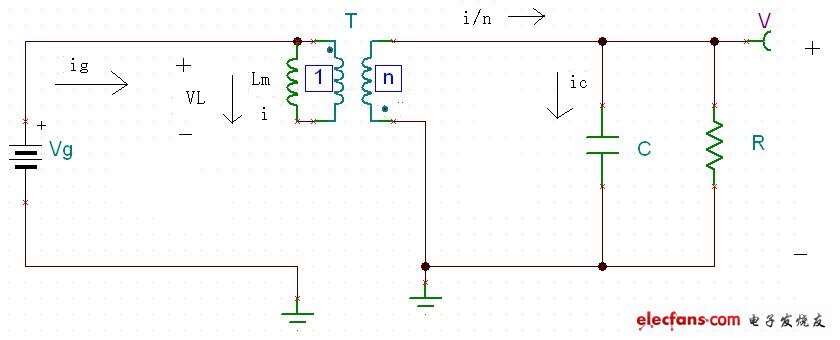
圖十五
在最開始的假設情況下,列寫狀態方程:
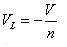????(24)
????(25)
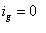????(26)
這個狀態持續時間為 ,Lm中的電流i在二次側折射電壓的作用下,開始線性減少,斜率為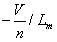
.能量轉移到輸出.
在經過一個周期的折騰后,電感Lm電流回到周期開始的點,C上的電壓回到周期開始的點.因為,這是一個工作在和諧狀態下的電路.所以有:
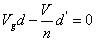?? (27)
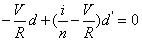?? (28)
輸入電流ig的周期平均值為:
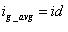????(29)
解等式 27 和等式 28 得:
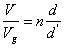????(30)
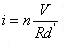????(31)
對比等式 30 和等式 8 以及等式 31 和等式 9. 發現沒有,是不是buck-boost和flyback的直流增益很像?也說明了,flyback是由buck-boost演變而來的.?
下面研究Mosfet和二極管D所承受的電壓.
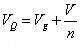?? (32)
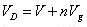????(33)
用等式(30)來做簡化,則有:
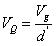????(34)
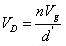????(35)
電感紋波電流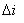
的算法,在等式 13 中已經給出.
同樣假設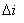
設計為i的5%.則通過Mosfet的RMS電流油等式 15 給出.通過二極管D的RMS電流為:
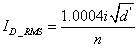????(36)
輸入的RMS電流等于Mosfet的RMS電流.
照前面的方法計算C的紋波電流的RMS值為:
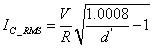????(37)
紋波電壓為:
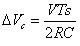????(38)
到現在為止,好像CCM-flyback的draft(這里我實在找不到一個合適的詞來形容,所以就只好用這個字了.希望都能明白這個字后面的意思)設計呼之欲出了啊.
到這里,如果正好你也看過了 菜鳥課堂1 的話,那恭喜你,你已經是初級的ccm-flyback設計師了.可以開始做自己的flyback了,雖然性能還很差,也許變壓器還會飽和,可能還會響,但不管怎樣,這是第一個哦.
今天最后附上一個禮物送給大家,CCM-flyback的參數計算表格.
工作在DCM情況下的flyback比在CCM下多了一個工作狀態 3. 工作狀態1 和工作狀態2 與CCM的工作狀態1 和2 相同,在工作狀態3下,Mosfet Q 和二極管D都處于關斷狀態.三個工作狀態分別如圖十六,圖十七, 圖十八所示.經歷時間分別為d1Ts,d2Ts,d3Ts.
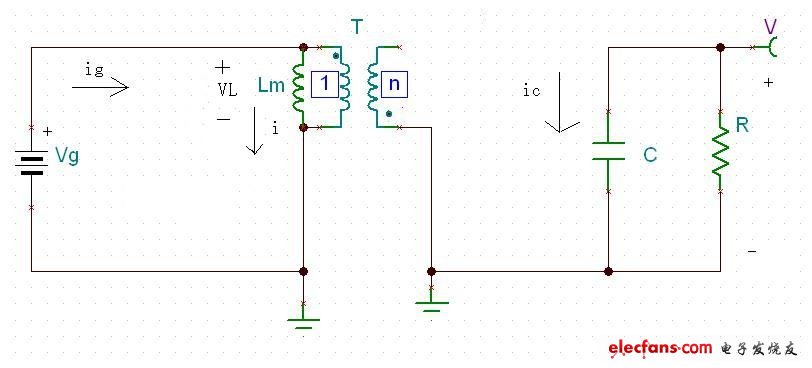
圖十六
?
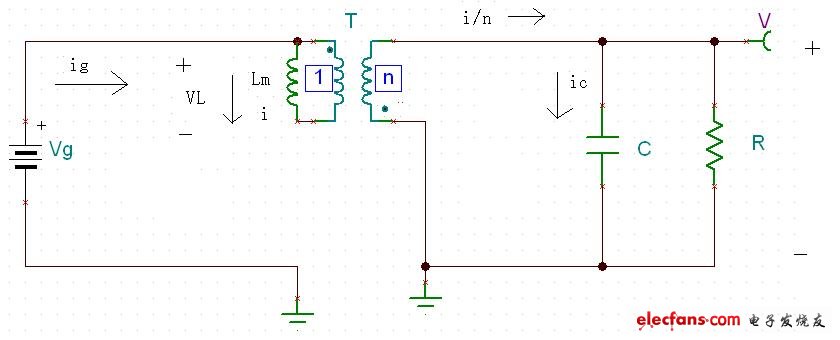
圖十七
?
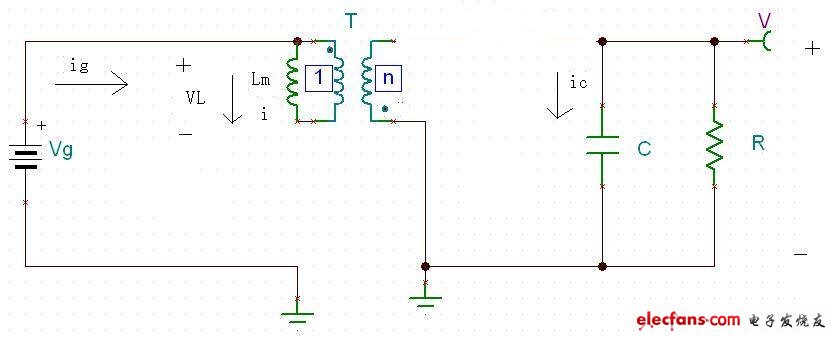
圖十八
?
分別對3個狀態列寫狀態方程.
?
狀態1有:
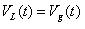??(39)
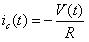?? (40)
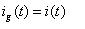?? (41)
狀態2 有:
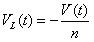?? (42)
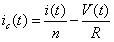?? (43)
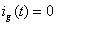?? (44)
狀態3有:
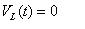????(45)
????(46)
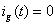????(47)
一個好的設計,輸出電壓V的紋波比電壓V小很多.忽略電壓紋波,有:
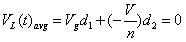???? (48)
從等式 48 中得到的V/Vg的表達式中含有d2,這個不是想要的形式.想辦法把d2消去. C里面只流過紋波電流,直流成分都輸出給負載.所以通過二極管D電流的平均值就等于輸出到負載上的電流.
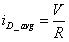???? (49)
二極管的平均電流也可以這樣子計算(因為是三角波):
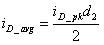???? (50)
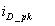表示的是流過二極管的峰值電流.與ipk的的關系是:
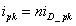???? (51)
ipk是可以計算的,表示為:
???? (52)
解 等式 48 到52 可得:
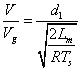???? (53)
把Lm用Lsec來表示,則等式 53 可以寫成(d1就是占空比d):
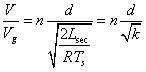????(54)
請牢牢記住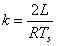
的這種形式吧,會有很多地方用到的.
把 等式 54 帶回到 等式 48中,則可得:
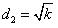????(55)
按照慣例,先計算下Mosfet Q和二極管D的最大電壓.
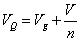????(56)
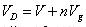????(57)
流過Mosfet Q,二極管D和電容C的RMS電流表示為:
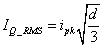???? (58)
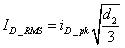???? (59)
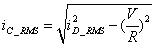???? (60)
工商網監
評論